一种安全的PKI与IBC之间的双向异构数字签名方案
2021-04-16孟博王潇潇郑绪睿刘琴
孟博,王潇潇,郑绪睿,刘琴
(中南民族大学 计算机科学学院,武汉 430074)
随着网络应用环境变得越来越复杂, 通信双方极有可能支持不同的密码体制, 因此现有的基于同构环境(通信双方支持相同密码体制)的安全机制不能满足异构环境(通信双方支持不同密码体制)中网络通信安全的需要.文献[1-19]提出异构签密方案,实现机密性和认证性.但是在许多异构应用场景中,仅需要认证性,比如网络公告栏,不需要机密性.在这种情况下,如果应用异构签密,通信成本高,代价大.因此融合异构签密和数字签名思想,首先提出异构数字签名的概念,异构数字签名是指,在异构环境下,对消息进行数字签名,进而提出一种安全的公钥基础设施(public key infrastructure,PKI)与基于身份加密(identity-based cryptography,IBC)之间的双向异构数字签名方案.在异构环境下,实现对消息的异构数字签名,保障异构环境中的网络通信安全.
1 相关工作
本文工作主要涉及到数字签名和异构签密.首先介绍数字签名的相关工作,然后讨论异构签密的相关内容.数字签名是密码学的一个重要分支.2015年,杨晓峰等[20]提出了基于PKI的可信二维码方案,使用RSA算法进行数字签名和认证.同年,孙善宝[21]结合PKI和证书权威机构(certificate authority,CA)、时间戳、手写签名识别等,提出一种随机个体数字签名认证方案.2018年,张键红等[22]结合基于身份的密码体制和多重数字签名算法,提出了一种高效的安全的多重数字签名方案.2015年,甄平等[23]利用Chebyshev公钥算法,提出一种基于身份的前向安全数字签名算法,支持签名的前向安全性.
异构签密(Heterogeneous Signcryption)概念由孙英霞等[1]提出,此外她们还提出一种基于传统公钥密码体制和基于身份公钥密码体制之间的签密方案,但是不满足不可否认性.2016年,张玉磊等[5]提出无证书公钥加密(certificateless public key cryptography,CLPKC)→传统的公钥基础设施(traditional public key infrastructure,TPKI)异构签密方案,该方案满足密文匿名性,可以有效地保护收发双方的身份隐私.2017年,张玉磊等[6]提出PKI与CLC环境的双向异构签密方案,实现了异构环境之间数据的安全传输.同年,王彩芬等[7]提出基于 PKI 和 IBC 的双向匿名异构签密方案.2018年,刘景伟等[10]提出两个PKI和CLC之间的无双线性对的签密方案.2019年,曹素珍等[11]提出了改进的PKI→IBC方案和IBC→PKI方案,并在随机预言模型下给出安全证明.2017年,葛丽霞等[24]提出了异构指定验证者签名方案,包含HSDVS-I方案和HSDVS-II方案,对HSDVS-II方案分析后,发现正确性和不可传递性的证明过程错误,因此,HSDVS-II方案不满足正确性和不可传递性.
2 预备知识
2.1 异构环境
异构环境是指,在此环境中,通信双方支持的密码体制不同,如,用户A属于无证书环境,用户B属于公钥基础设施环境,此时,用户A和用户B之间的通信处于异构环境.
2.2 双线性Diffie-Hellman问题
首先介绍双线性对的性质,然后介绍双线性Diffie-Hellman问题(BDHP, Bilinear Diffie-Hellman problem).
双线性对的性质:
假设G1是阶为素数q的循环加法群,G2是阶为素数q的循环乘法群,双线性对e:G1×G1→G2满足以下性质:
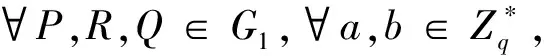
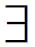


BDHP问题:
已知G1是一个阶为素数q的循环加法群,P是G1的一个生成元,G2是一个阶为素数q的循环乘法群,G1和G2之间满足双线性映射e,e:G1×G1→G2.
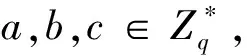
3 PKI与IBC之间异构数字签名方案
基于BDHP问题,提出PKI与IBC之间的双向异构数字签名方案,支持正确性、不可伪造性和不可否认性.该方案包含PKI→IBC异构数字签名方案和IBC→PKI异构数字签名方案.PKI与IBC之间的双向异构数字签名方案由设置系统公共参数、密钥生成、生成签名和验证签名4个算法组成,下面介绍这4个算法.
设置系统公共参数:输入安全参数k,私钥生成中心(private key generation,PKG)生成系统主公钥、主密钥,输出系统公共参数param,保留系统主密钥s.
密钥生成:PKI环境中的用户公钥为PKA,私钥为SKA,密钥对为(PKA,SKA),IBC环境中的用户公钥为PKB,私钥为SKB,密钥对为(PKB,SKB).PKI环境中的用户向CA提交自己的身份IDA,CA给用户颁发证书,用户设置私钥,计算对应的公钥,公钥与CA颁发的证书绑定,输出结果为公钥PKA、私钥SKA.IBC环境中的用户向PKG提交自己的身份IDB,PKG根据用户的身份设置私钥,发送给用户,用户计算公钥,输出结果为公钥PKB、私钥SKB.
生成签名:签名者生成签名.输入消息m、签名者的公钥、私钥、验证者的公钥,执行算法Sign(σ,m,PKS,SKS,PKV),其中,S表示签名者,V表示验证者,输出签名σ.签名者发送δ=(σ,m)给验证者.
验证签名:验证者验证签名.验证者收到签名,输入消息m,签名者的公钥、验证者的私钥,执行算法Verify(σ,m,PKS,SKV),其中,S表示签名者,V表示验证者,验证者接受签名或者输出错误符号⊥.
3.1 设置系统参数和密钥生成
PKI→IBC异构数字签名方案和IBC→PKI异构数字签名方案采用相同的系统公共参数和密钥生成两个算法.下面介绍设置系统参数和密钥生成两个算法.
设置系统参数:
系统参数由可信第三方PKG生成,输入一个安全参数为k,PKG选择阶为素数q的循环加法群G1和阶为素数q的循环乘法群G2,P是G1的一个生成元,定义一个双线性对e,e:G1×G1→G2.
公开系统参数:param={k,q,G1,G2,P,e,H1,H2,Ppub},保留主密钥s.
密钥生成:
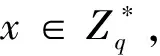
IBC环境中的用户向PKG提交自己的身份IDB,PKG计算用户的私钥SKB=sH1(IDB),发送给用户,其中,PKB=H1(IDB)为用户的公钥.IBC环境中的用户的公钥为PKB,私钥为SKB,PKB=H1(IDB),SKB=sH1(IDB),密钥对为(PKB,SKB).
设置系统参数与密钥生成两个算法的结果如下:
(1)设置系统参数的结果.
公开系统参数:param={k,q,G1,G2,P,e,H1,H2,Ppub},保留主密钥s.
(2)密钥生成的结果.
密钥生成:
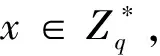
3.2 PKI→IBC异构数字签名方案
PKI→IBC异构数字签名方案,如图1所示,假设签名者是 PKI环境中的用户,验证者是IBC环境中的用户.签名者应用PKI密码体制生成异构数字签名,验证者应用IBC密码体制验证异构数字签名.该方案包含两个步骤:生成签名,如图2所示,验证签名,如图3所示.
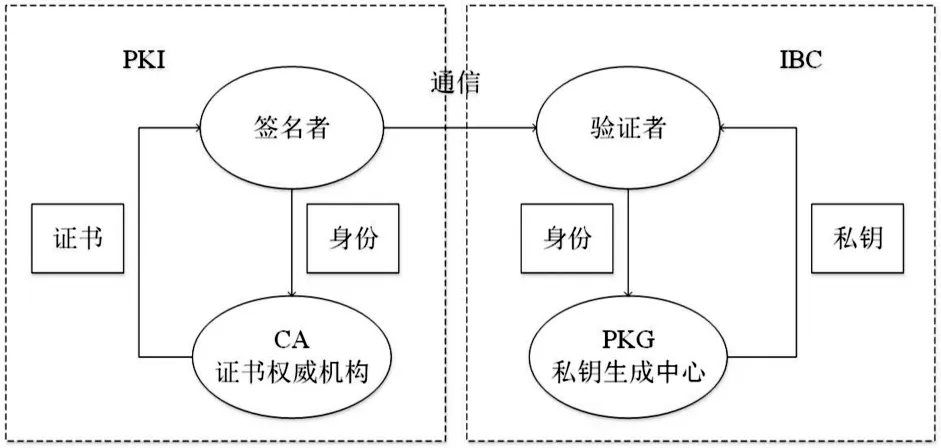
图1 PKI→IBC异构环境
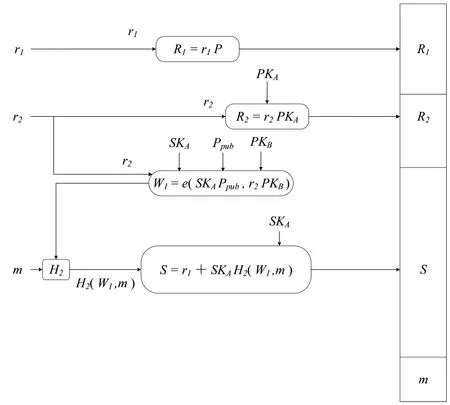
图2 PKI→IBC异构数字签名方案中签名者生成签名
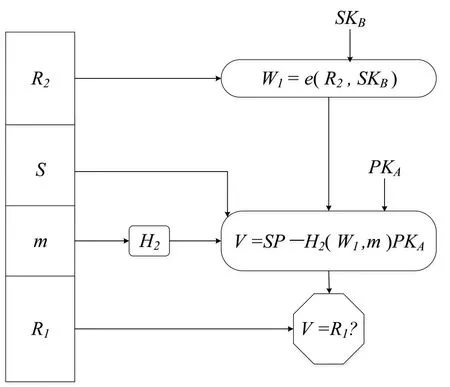
图3 PKI→IBC异构数字签名方案中验证者验证签名
(1)生成签名.
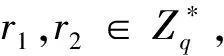
计算W1=e(SKAPpub,r2PKB).
计算S=r1+SKAH2(W1,m).
签名为σ=(R1,R2,S),签名者发送δ=(σ,m)给验证者.
(2)验证签名.
验证者的密钥对为(PKB,SKB),PKA是签名者的公钥,验证者收到δ=(σ,m)之后,验证δ,输入信息为δ=(σ,m).
计算W2=e(R2,SKB).
计算V=SP-H2(W2,m)PKA.
验证V=R1等式成立情况,若等式成立,验证签名成功,接受签名,输出1;否则输出错误符号⊥.
定义1:正确性:一个有效的异构数字签名能够成功通过验证算法的验证.
证明PKI→IBC异构数字签名方案的正确性:
W1=e(SKAPpub,r2PKB)=e(SKAsP,r2PKB)=e(SpKA,r2PKB)=e(PKA,r2SKB)=e(r2PKA,SKB)
W2=e(R2,SKB)=e(r2PKA,SKB)
故W1=W2
V=SP-H2(W2,m)PKA=(r1SKA+H2(W1,m))P-H2(W2,m)PKA
∵W1=W2
∴H2(W1,m)=H2(W2,m)
∴V=R1=r1p
证明签名δ=(σ,m)满足验证等式V=R1,由结果可知,V=R1=r1P,所以,PKI→IBC异构数字签名方案的正确性得证.
3.3 IBC→PKI异构数字签名方案
IBC→PKI异构数字签名方案,如图4所示,假设签名者是PKI环境中的用户,验证者是IBC环境中的用户.签名者应用IBC密码体制生成异构数字签名,验证者应用PKI密码体制验证异构数字签名.该方案包含两个步骤:生成签名,如图5所示,验证签名,如图6所示.

图4 IBC→PKI异构环境

图5 IBC→PKI异构数字签名方案中签名者生成签名

图6 IBC→PKI异构数字签名方案中验证者验证签名
(1)生成签名.
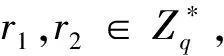
计算W1=e(SKB,r2PKA).
计算S=r1PKB+SKBH2(W1,m).
签名为σ=(R1,R2,S),签名者发送δ=(σ,m)给验证者.
(2)验证签名.
验证者的密钥对为(PKA,SKA),PKB表示签名者的公钥,验证者收到δ=(σ,m)之后,验证δ,输入信息为δ=(σ,m).
计算W2=e(PKBSKA,r2Ppub).
计算h=H2(W2,m).
验证e(S,P)=e(R1+hPpub,PKB)等式成立的情况,若等式成立,验证签名成功,接受签名,输出1;否则输出错误符号⊥.
证明IBC→PKI异构数字签名方案的正确性:
W1=e(SKB,r2PKA)=e(sPKB,r2SKAP)=e(PKBSKA,r2Ppub)
W2=e(PKBSKA,r2Ppub)=e(SKB,r2PKA)
则W1=W2
e(S,P)=e(r1PKB+SKBH2(W1,m),P)=e(r1PKB,P)e(SKBH2(W1,m),P)=e(R1,PKB)e(PKBH2(W1,m),Ppub)
因W1=W2,h=H2(W2,m)
故H2(W1,m)=H2(W2,m)
则e(S,P)=e(R1+hPpub,PKB)
证明签名δ=(σ,m)满足验证等式e(S,P)=e(R1+hPpub,PKB),由结果可知,e(S,P)=e(R1+hPpub,PKB),所以,IBC→PKI异构数字签名方案的正确性得证.
4 不可伪造性证明
4.1 不可伪造性的证明模型
不可伪造性指,除非攻击者获得签名人或者验证者的私钥,否则,不能生成一个有效的签名.即:利用公共的密钥以及公开的系统参数等公开的信息无法生成签名者的签名,使得验证等式成立.孙英霞等[1]提出的不可伪造性模型中,询问阶段只包含密钥生成询问阶段、签密询问阶段和解签密询问阶段,但是没有涉及伪造阶段,故不能直接用来分析提出方案的不可伪造性,因为本方案的不可伪造性证明基于伪造签名的分叉引理.故基于随机预言机模型,提出不可伪造性安全证明模型,模型包含3个阶段:初始化参数,询问阶段,伪造阶段,其中,F表示挑战者,AII表示敌手,敌手AII是挑战者F的一个子程序.
(1)初始化参数.
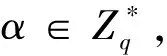
(2)询问阶段.
询问阶段:敌手AII执行以下询问:哈希询问、密钥提取询问、签名询问、验证询问,挑战者F维护初始值为空的列表,记录Hi(1≤i≤2)预言机和公钥询问信息,返回对应的回答.
哈希询问:挑战者F维护哈希列表,进行询问的身份为IDi,挑战者F从哈希列表中查找,存在对应的记录,返回对应的哈希值;如果不存在,挑战者F随机选择,将随机结果返回给敌手AII,将返回结果存入列表中.
密钥提取询问:敌手AII对PKI与IBC环境的用户公钥和私钥进行询问,IDi表示PKI环境中用户的身份,IDj表示IBC环境中用户的身份, 将返回结果存入列表中.
签名询问:挑战者AII运行生成签名的算法,返回签名δ=(σ,m).
验证询问:敌手AII对签名进行验证询问,如果IDA=IDi,IDB=IDj,停止询问.否则,挑战者F计算验证者的私钥,代入验证等式,验证签名的真实性,若等式成立,接受签名,输出1;否则,输出错误符号⊥.
(3)伪造阶段.
伪造阶段:敌手AII输出伪造的签名.
敌手AII输出关于消息m′的一个签名δ′=(σ′,m′),其中,i表示签名者,j表示验证者,如果IDi=IDA,并且IDj=IDB,敌手AII成功伪造签名δ′;否则,挑战失败.
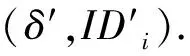
敌手AII输出一个等式类似于W1=e(P,P)abc形式的解作为BDH问题的一个实例解.
证毕.
4.2 证明PKI→IBC异构数字签名方案不可伪造性
定理1:PKI→IBC的异构数字签名方案是不可伪造的.
证明如下:
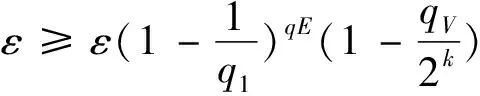
证明:挑战者F输入BDH问题的实例(P,aP,bP)∈G1,目标是计算e(P,P)ab.
(1)初始化参数.
敌手AII进行多次询问,挑战者F维护初始为空的表l1-l3.
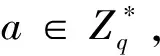
(2)询问阶段.
敌手AII执行以下询问,挑战者F返回对应的回答.
哈希询问:
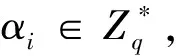
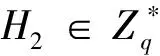
密钥提取询问:
敌手AII对PKI与IBC环境的用户公钥和私钥进行询问.
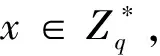
PKI私钥询问: 敌手Aii询问IDi私钥时,AII从表l1中得到(i,IDi,PKi,xi),返回SKi=xi.
IBC公钥询问:敌手AII询问IDj公钥时,即做H1询问,若IDj=IDB,模拟结束;若IDj≠IDB,挑战者F首先查表H1-list,返回bP,存入表l2中.
IBC私钥询问:敌手AII询问IDj私钥时,若IDj=IDB,模拟结束;若IDj≠IDB,挑战者F首先查询表H1-list,返回sH1(IDj),存入表l3中.
签名询问:
如果敌手AII对消息m进行签名询问, 其中验证者的身份为IDj, 挑战者F做如下回答:
如果签名者既不是真正的签名者也不是真正的验证者,那么挑战者F就可以运行签名算法返回一个签名,生成签名过程为:
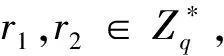
计算双线性对W1=e(SKiPpub,r2PKB).
计算S=r1+SKiH2(W1,m).
挑战者F输出签名δ=(σ,m)=(R1,R2,S,m)给敌手AII.
验证询问:
如果敌手AII对签名进行验证询问,签名者的身份为IDi,验证者的身份为IDi,如果IDi=IDA,并且IDj=IDB,模拟结束;否则,挑战者F计算验证者IDj的私钥,计算V=SP-H2(W2,m)PKi,验证等式V=R1的成立情况,若等式成立,接受签名,输出1,否则,输出错误符号⊥.
(3)伪造阶段.
敌手AII输出关于消息m′的一个签名δ′=(σ′,m′),其中i表示签名者,j表示验证者,如果IDi=IDA,并且IDj=IDB,敌手AII成功伪造签名δ′;否则,挑战失败.
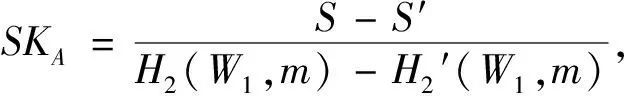
证毕.
4.3 证明IBC→PKI异构数字签名方案不可伪造性
定理2:IBC→PKI的异构数字签名方案是不可伪造的.
证明如下:
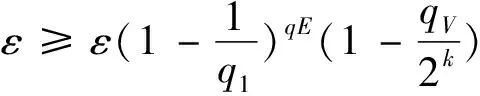
证明:挑战者F输入BDH问题的实例(P,aP,bP)∈G1,目标是计算e(P,P)ab.
(1)初始化参数.
敌手AII进行多次询问,挑战者F维护初始为空的表l1-l3.
(2)询问阶段.
敌手AII执行以下询问,挑战者F返回对应的回答.
哈希询问:
H1询问:同定理1的H1询问,返回的询问结果如下:
H2询问:同定理1的H2询问.
密钥提取询问:
敌手AII对PKI与IBC环境的用户公钥和私钥进行询问.
PKI公钥询问:同4.2的PKI公钥询问.
PKI私钥询问:同4.2的PKI私钥询问.
IBC公钥询问:同4.2的IBC公钥询问.
IBC私钥询问:同4.2的IBC私钥询问.
签名询问:
如果敌手AII对消息m进行签名询问,其中验证者的身份为IDi,挑战者F做如下回答:
如果签名者既不是真正的签名者也不是真正的验证者,那么挑战者F就可以运行签名算法返回一个签名,生成签名过程为:
挑战者F生成签名者的私钥SKj=sH1(IDj),计算双线性对W1=e(SKj,r2PKA),h1=H2(W1,m).
计算S=r1PKj+h1SKj.
挑战者F输出签名δ=(σ,m)=(R1,R2,S,m)给敌手AII.
验证询问:
如果敌手AII对签名进行验证询问,签名者的身份为IDi,验证者的身份为IDj,如果IDi=IDA,并且IDj=IDB,模拟结束;否则,挑战者F计算验证者IDj的私钥,计算W2=e(SKj,r2P)SKA,计算h=H2(W2,m),验证等式e(S,P)=e(R1+h2Ppub,PKj)的成立情况,若等式成立,接受签名,输出1,否则,输出错误符号⊥.
(3)伪造阶段.
敌手AII输出关于消息m′的一个签名δ′=(σ′,m′),其中i表示签名者,j表示验证者,如果IDi=IDA,并且IDj=IDB,敌手AII成功伪造签名σ′;否则,挑战失败.
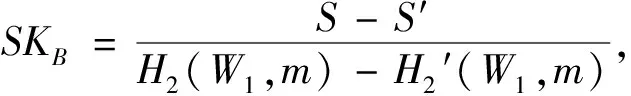
5 不可否认性分析
不可否认性是指生成签名步骤中,生成的签名中包含签名者的密钥信息,签名者不能否认自己的签名.下面分析PKI→IBC异构数字签名方案和IBC→PKI异构数字签名方案不可否认性.
5.1 PKI→IBC异构数字签名方案的不可否认性
PKI→IBC方案的生成签名步骤中,生成的签名σ=(R1,R2,S)中包含签名者的密钥信息SKA,签名者不能否认自己的签名.所以,本方案可以实现不可否认性.
5.2 IBC→PKI异构数字签名方案的不可否认性
IBC→PKI方案的生成签名步骤中,生成的签名中σ=(R1,R2,S)包含签名者的密钥信息SKB,签名者不能否认自己的签名.所以,本方案可以实现不可否认性.
6 性能分析
对提出的双向异构数字签名方案从签名计算量、解签密计算量、总计算量4个方面进行分析和讨论,此外,据我们所知,目前不存在其他的异构数字签名方案,故与异构签密方案[13,15,17]进行比较,发现,提出方案总计算量最小,如表1所示,其中,xor表示异或运算,pair表示双线性对运算,hash表示哈希运算,exp表示指数幂运算.
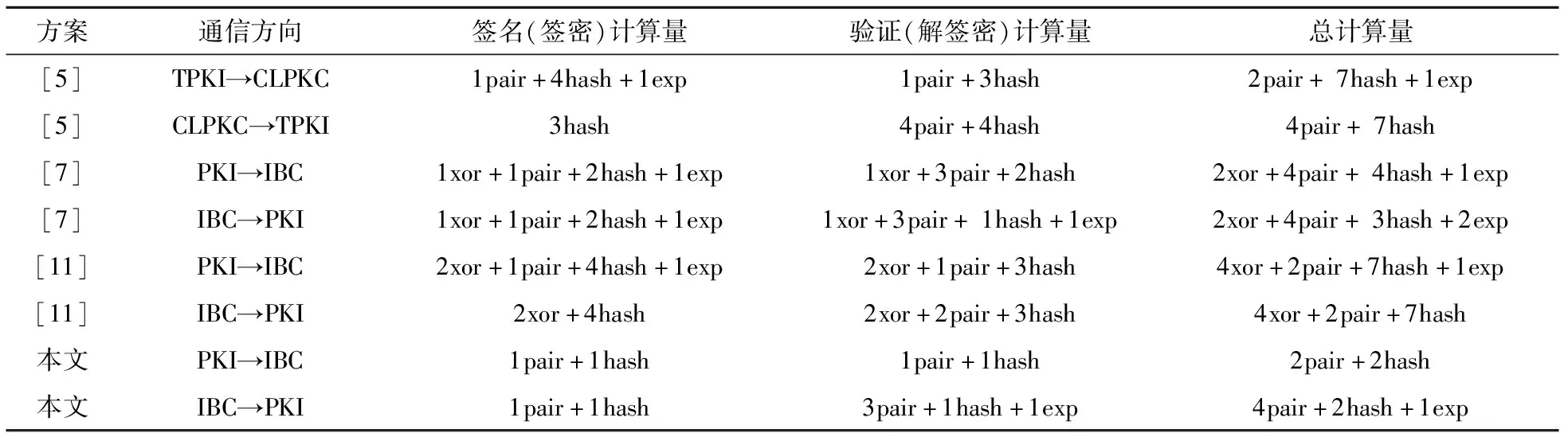
表1 性能比较
提出的PKI→IBC异构数字签名方案的签名阶段的计算量为1pair+1hash,包含1个哈希运算,验证阶段的计算量为1pair+1hash,包含1个哈希运算,IBC→PKI异构数字签名方案的签名阶段的计算量为1pair+1hash,包含1个哈希运算,验证阶段的计算量为3pair+1hash+1exp,包含1个指数幂运算和1个哈希运算.
异构签密方案中包含签名和加密操作,但是提出的异构数字签名方案中包含签名,不需要对消息做加密和解密,即异或运算,签名阶段无指数幂运算,验证阶段1个指数幂运算,因此总计算量最小,效率最高.
7 文献[24]中方案的安全性分析
文献[24]中的方案包含HSDVS-I方案和HSDVS-II方案,对HSDVS-II方案分析后,发现正确性和不可传递性的证明过程存在错误.
正确性证明过程:
e(Z,H1(IDB)P+Ppub=
e(rr1SB+r2P,H1(IDB)P+Ppub)=
e(r1SB,H1(IDB)P+Ppub)r·
e(r2P,H1(IDB)P+Pput)=
e(r1,P,P)r·e(r2P,H1(IDB)P+Ppub)=
Wr·e(r2P,H1(IDB)P+Ppub)=
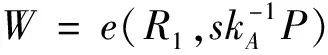
不可传递性证明过程:
e(Z′,H1(IDB)P+Ppub=
在不可传递性证明过程中,文献[24]将Z′=a+r′b代入e(Z′,H1(IDB)P+Ppub中证明,但是在指定验证者模拟的签名副本(R1′,R2′,R3′,Z′,m)中,Z′=r′a+b,不能证明等式
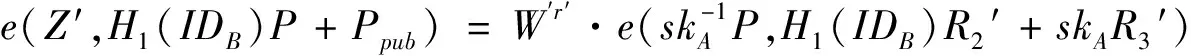
下面给出正确的不可传递性证明:
e(Z′,H1(IDB)P+Ppub)=
8 结语
为保障异构环境网络安全,提出了安全的PKI和IBC之间的双向异构数字签名方案,方案在满足正确性的基础上,实现不可伪造性和不可否认性,使用随机预言机模型对方案的不可伪造性进行证明,与已有的典型异构签密方案相比,提出的方案在异构环境下,实现对消息的异构数字签名,实现了对消息源的认证.构造计算效率更高的方案是下一步的研究方向.
