喀斯特地区地表温度空间降尺度方法初探

尹 枷 愿，蔡 宏*，田 鹏 举，唐 敏

(1.贵州大学矿业学院，贵州 贵阳 550025；2.贵州省生态气象和卫星遥感中心，贵州 贵阳 550025)

0 引言

地表温度(LST)是大气与地表能量循环中最重要的参数之一[1]，被广泛应用于水文平衡评估、全球变暖研究、城市热岛效应评估和地表蒸散量计算等领域[2-7],然而，受热红外传感器成像条件的影响，地表温度数据产品常因时空分辨率相互制约而无法满足实际应用需求。为此，不少学者提出地表温度降尺度方法以解决该问题，其实质是将其他高分辨率数据信息整合到热红外波段上，以此提高地表温度分辨率。常用的地表温度降尺度方法主要分为基于图像融合降尺度方法和基于尺度因子的统计回归降尺度方法[8]，后者着重研究影响LST变化的物理因素，因操作简单、精度高等而得到广泛应用。

早期统计回归降尺度研究主要探究LST与归一化植被指数(NDVI)[9]、植被覆盖度(VC)[10-12]等植被指数之间的线性关系，并成功应用于地形均匀或同质地区，但在复杂地区的效率不高[13]。因此，不少学者加入更多凸显地形变化和地表类型的尺度因子，例如：Maeda利用海拔、NDVI与LST之间的线性回归关系进行山区降尺度研究[14]；Duan等通过地理加权回归方法建立NDVI和DEM之间的非平稳关系，并成功将河北省华北平原与内蒙古高原过渡地带的LST从1 km降尺度至90 m[15]。尽管传统的统计回归方法取得了一定成效，但考虑到尺度因子与LST之间复杂的非线性关系，一些学者建议将贝叶斯[16]、人工神经网络[17]、支持向量机[18]和随机森林(RF)[19]等机器学习模型用于地表温度降尺度。其中，RF具有实现简单、不易过拟合的特点，能更好地模拟LST与地形、地貌间的关系。例如：Hutengs等利用DEM、土地覆盖图、红光与近红外波段的反射率同LST建立RF模型，在地中海东部高程变化大的植被地区，将LST从1 km降尺度到250 m[19]；Wu等利用地表反射率、光谱指数、地形因子和土地利用图，对以自然地表为主的西班牙塞哥维亚佩尼亚罗拉山区和北京平原城区进行了降尺度研究[20]。然而，目前考虑喀斯特山区地形地貌异质性特点的高精度地表温度降尺度鲜有研究。因此，本文以遵义市西北部和贵阳市以南地区为研究区，选择适合喀斯特山区的尺度因子，以MODIS 第31、32波段的辐射亮度为因变量，建立一种适合喀斯特地区的随机森林(Karst Random Forest,KRF)模型，并以Landsat-8反演的地表温度数据为验证数据进行精度评定。

1 研究区及数据

考虑到喀斯特地区地形起伏度相差较大，本研究选择两个有代表性的区域(图1)，以充分探究KRF模型的适用性。区域a位于遵义市西北部，为喀斯特山区向平原过渡的盆地边缘地带，处于副热带东亚大陆季风区内，属于中国亚热带高原季风湿润气候，区域内地势起伏较大(最高海拔为1 730 m，最低海拔为316 m，高差为1 414 m)，地表覆盖类型主要为自然地表及小部分建设用地和水体；区域b位于贵阳市以南，为典型喀斯特山区城市，最高海拔约为1 660 m，最低海拔约为991 m，高差为669 m，气候类型与区域a相同，地表覆盖类型主要有建设用地、水体、裸土、裸岩等。

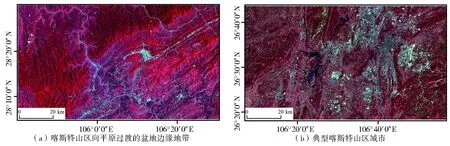
图1 研究区示意

研究数据(表1)包括：1)MODIS数据，来源于NASA(https://ladsweb.modaps.eosdis.nasa.gov/)，选用其MOD021KM和MOD11A1 产品，轨道号为h27v06，成像时间分别为2016年7月26日和2018年3月4日，利用NASA发布的HEGTool软件将该数据重投影为WGS-84/UTM。2)Landsat-8 OLI/TIRS数据，来源于地理空间数据云(http://www.gscloud.cn/)，区域a条带编号为128，行编号为40，选取与MODIS同一天(2016年7月26日)的数据；区域b条带编号为127，行编号为42，由于贵阳地区云雾较大，无法获取同一天的数据，通过对历史气象站数据查证，选取成像时间与MODIS日期相近的2018年3月3日的Landsat-8影像作为参考影像。3)高程数据，来源于地理空间数据云的ASTER GDEM V2，时间为2015年1月6日，条带编号为105、106，行编号为26、28。以上影像利用ENVI进行辐射定标、大气校正、镶嵌和裁剪等预处理。

2 喀斯特地区地表温度空间降尺度方法

喀斯特地区地表温度空间降尺度流程包括尺度因子选取、RF热红外降尺度模型构建、热红外地表温度反演和精度评价四部分(图2)。

2.1 尺度因子选取

尺度因子会影响降尺度方法的精度，本研究针对喀斯特地区的特点，添加了常规尺度因子和喀斯特地表特征尺度因子。

表1 研究数据信息

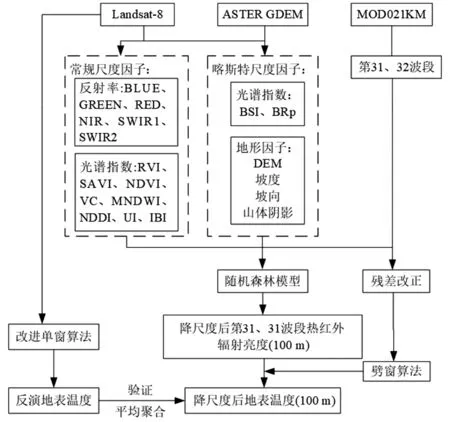
图2 喀斯特地区地表温度降尺度流程

2.1.1 常规尺度因子 着重考虑表征土地覆盖的相关指数，筛选后的参数包括Landsat-8 OLI的红、蓝、绿、近红外和短波红外波段的反射率以及Landsat-8 OLI反演的遥感指数：表征植被的比值植被指数(RVI)、土壤调整植被指数(SAVI)、归一化植被指数(NDVI)、植被覆盖度(VC)，表征水体的改进归一化水体指数(MNDWI)、归一化干旱指数(NDDI)，表征城镇的城市指数(UI)、建筑用地指数(IBI)。

2.1.2 喀斯特地表特征尺度因子 Deng等在研究喀斯特地区土地利用、NDVI与LST的关系时，发现低植被覆盖的裸岩与裸土区域存在异常高温[21]，孟鹏燕等发现地形是影响LST的重要因素[22]，因此，除常规尺度因子外，本文在地貌上选择裸土指数(BSI)[23](式(1))和裸岩率(BRp)[24](式(2))，地形上选择由ASTER GDEM数据得到的高程因子，包括高程、坡度、坡向、山体阴影。所有尺度因子的空间分辨率均为30 m，通过平均聚合到1 km与MODIS数据进行降尺度建模。

(1)

BRp=1-BSp-VC

(2)

式中：ρmir为中红外波段反射率，本文用Landsat-8的短波红外波段1代替;ρred、ρnir、ρblue分别为红光、近红外、蓝光波段的反射率;BSp为土壤裸露率；VC为植被覆盖度。

2.2 基于RF算法的热红外降尺度模型构建

贵州喀斯特地区地表形态特殊，景观破碎且异质性强，复杂的地表环境使尺度因子对地表温度的响应关系复杂，因此，本研究考虑尺度因子与热红外辐射亮度之间的非线性关系，引入随机森林(RF)算法进行建模。该算法由大量不相关的决策树构成，通过bootstrap重抽样方法，首先将原始训练样本中抽取的多个样本自主合并，生成训练样本合集，然后根据自助样本集生成多个决策树并组成随机森林，最终结果由所有决策树平均而得，具有精度高、对多元线性不敏感的特点。

基于尺度因子的LST降尺度方法的本质是：不同尺度下LST和尺度因子之间的定量关系保持不变，即在低空间分辨率尺度下建立的关系模型，在高空间分辨率尺度下依然适用。降尺度模型的表达式为：

(Bi)C=f((Ak)C)

(3)

ΔC=(Bi)O-(Bi)C

(4)

(Bi)F=f((Ak)F)+ΔC

(5)

式中：i=31、32，分别代表MODIS第31、32波段；(Bi)C为模型计算得到的第31、32波段低分辨率辐射亮度；(Ak)C为通过平均聚合得到的低空间分辨率的尺度因子，k为尺度因子数量；f(·)为RF回归映射关系；ΔC为原始影像与预测影像之间的残差；(Bi)O为第31、32波段原始辐射亮度；(Bi)F为模型计算的第31、32波段高分辨率辐射亮度；(Ak)F为高分辨率的尺度因子。

本文中RF模型在Python平台上实现，其中关键参数为决策树的数量(n_estimators)和树的最大特征数量(max_features)，通过交叉验证、遍历优化，最终确定区域a第31波段RF模型的n_estimators=290，max_features=17，第32波段RF模型的n_estimators=375，max_features=13；区域b第31波段RF模型的n_estimators=390，max_features=11，第32波段RF模型的n_estimators=391，max_features=14。

2.3 热红外地表温度反演

现有LST反演算法主要包括单通道算法、劈窗算法和多通道多角度算法3类。针对不同的传感器，选择不同的反演方法能有效提高反演精度。

2.3.1 MODIS地表温度反演 MODIS第31、32波段的中心波长接近于AVHRR的第4、5通道，适宜用劈窗算法进行LST反演，因此本文选用覃志豪等的劈窗算法[25]，对降尺度后的第31、32波段辐射亮度进行反演，得到LST。反演公式为：

Ts=A0+A1T31-A2T32

(6)

(7)

(8)

(9)

Ci=εiτi(θ)

(10)

Di=[1-τi(θ)][1+(1-εi)τi(θ)]

(11)

式中：T31、T32分别为MODIS第31、32波段的亮温，通过普朗克公式计算；Ai、Ci、Di为参数；a31、b31、a32和b32根据波段特征确定，在地表温度0～50 ℃范围内，分别取a31=-64.60363，b31=0.440817，a32=-68.72575，b32=0.473453；εi为地表比辐射率，可由土地利用图和NASA提供的比辐射率计算；τi(θ)为大气透过率，可通过MOD021KM数据计算得到。

2.3.2 Landsat-8地表温度反演 Landsat-8 TIRS的第11波段不稳定，不宜反演地表温度，因此本文使用改进的单窗算法[26]对第10波段进行地表温度反演(式(12)-式(14))，用于降尺度验证。由于Landsat-8热红外波段的原始分辨率为100 m，所下载的为NASA重采样到30 m的数据，并与30 m的OLI数据进行了配准[27]，因此，本文参照张文奇等的方法，利用聚合平均法对TIR数据重采样后再验证[28]，即将Landsat-8第10波段从30 m重采样到100 m，再进行温度反演。

Ts=[a10(1-C10-D10)+(b10(1-C10-D10)+C10+D10)T10-D10Ta]/C10

(12)

C10=τ10ε10

(13)

D10=(1-τ10)[1+(1-ε10)τ10]

(14)

式中：a10和b10是第10波段的普朗克回归系数，分别取-62.7182和0.4339。

2.4 精度评价指标

为评估本文适合喀斯特地区的随机森林(KRF)方法的精度，分别与目前最常用的TsHARP算法(基于NDVI与LST间线性关系的经典降尺度算法)[9]和最新的MTVRF模型(基于反射率、非喀斯特光谱指数、土地覆盖图及高程等18个因子与LST间非线性关系的RF降尺度算法)[20]进行对比，并分别从总体和各地类两方面对降尺度结果进行定性和定量分析。定性方面主要对比3种降尺度方法得到的LST和Landsat-8反演的LST在空间分布特征上的差异；定量方面主要通过均方根误差(RMSE)、平均绝对误差(MAE)衡量降尺度结果与真实值间的偏差，其值越小，说明预测值与实际值的差值越小，降尺度精度越高；应用线性回归决定系数(R2)评定回归模型的拟合优度，R2越接近1，说明回归模型的拟合程度越高。具体计算公式如下：

(15)

(16)

(17)

3 结果与讨论

3.1 热辐射亮度和尺度因子的重要性评价

为探究热辐射亮度和尺度因子对降尺度的影响，首先将选定的20个尺度因子分别与MOD11A1的第31、32波段的热红外辐射亮度进行RF建模，交叉验证5次，得到区域a 尺度因子与MOD11A1数据的R2为0.477，小于第31波段R2(0.552)和第32波段R2(0.513)，区域b 尺度因子与MOD11A1数据的R2为0.556，小于第31波段R2(0.642)和第32波段R2(0.634)，这与Agathangelidis等[29]利用辐射亮度与尺度因子建模后精度更高的结论一致。因此，直接利用热红外辐射亮度进行降尺度能够有效减少误差，提高精度。

为进一步分析尺度因子对降尺度的影响，通过尺度因子与辐射亮度的RF模型，得到各尺度因子对不同波段辐射亮度的贡献度(图3)。由图3可知，DEM在两区域对不同波段的贡献度均较高，说明山区地表温度空间分布受地形变化引起的热环境差异影响，地形效应显著[30]；此外，区域a的BSI、RVI对不同波段辐射亮度的贡献度均较高，这可能是因为该区域为地形高差大的自然地表，地表温度空间分布主要受地形因素和表征自然地表的遥感参数控制；区域b中SWIR2的贡献度较高，这可能是因为该区域为城区，总体地表温度较高，而SWIR2波段对高温目标较敏感[31]。

图3 尺度因子贡献度评估

整体而言，不同尺度因子对热红外辐射亮度均有贡献，表明本文所选的尺度因子适用于研究区，但不同区域因地形地貌不同，因子的贡献度有所不同，而RF模型会根据所添加的因子与热红外辐射亮度的关系自行调节权重，因此，加入更多适合喀斯特地区的参数进行降尺度后，能更好地模拟出喀斯特地区不同地形地貌对热红外辐射亮度的影响，使降尺度模型在不同区域均表现出较高的精度，从而提高模型的普适性。

3.2 不同喀斯特区域降尺度精度评价

利用3种方法在两个代表性喀斯特区域分别对MODIS数据进行降尺度，结果如图4、图5(彩图见附录1)所示，并以Landsat-8反演的100 m LST为真实值进行对比，发现3种方法均可将LST的空间分辨率从1 km提高到100 m。其中，TsHARP算法只考虑植被与LST的线性关系，在植被与水体和城镇的边界处噪声较多，效果最差；MTVRF模型和本文KRF方法为多尺度因子降尺度模型，在两区域精度都较高，但KRF方法效果更优，尤其是在中温区和高温区的空间分布上可显示更多细节，更加精细地描绘出喀斯特地区热特征空间分布的差异性。

图4 区域a总体降尺度结果比较

图5 区域b总体降尺度结果比较

为更客观地比较3种降尺度方法在不同喀斯特地区的表现，分别计算各方法的MAE、RMSE和R2(表2)。可以看出，对于区域a，KRF方法的性能较好，其MAE和RMSE分别为2.1146 K、2.4652 K，较TsHARP算法分别减少了0.4439 K和0.6204 K，较MTVRF模型分别减少了0.1419 K和0.1302 K，R2较TsHARP算法有一定的提高，但较MTVRF模型有所下降。对于区域b，KRF方法的MAE为1.1363 K、RMSE为1.4521 K，较TsHARP算法分别减少了0.5084 K 和0.6953 K，较MTVRF模型分别减少了0.214 K 和0.2928 K，R2为0.7103，较TsHARP算法和MTVRF模型分别提高了0.3805和0.1556。综上可知，本文KRF方法在喀斯特地区效果最好，说明引入与喀斯特相关的指数有助于降尺度，且利用MODIS第31、32波段进行建模能够最大限度避免异常值。

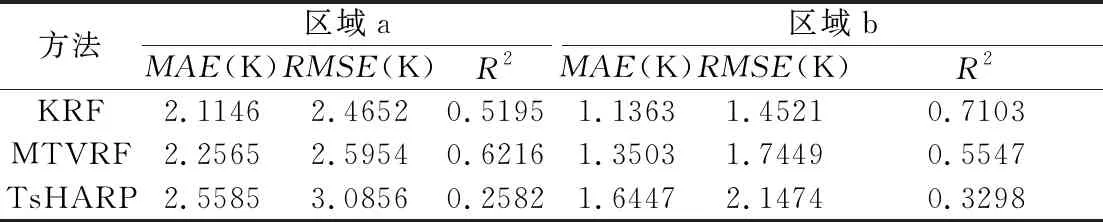
表2 喀斯特地区不同地形上的降尺度结果精度

另外，自然地表区域a的精度小于城市区域b的精度，这与Wu等[20]的研究结果相同，可能是因为地形变化对LST的影响更大。因此，利用KRF方法虽能明显提高喀斯特地区的地表温度降尺度精度，但在地形起伏度相对较小的喀斯特山区城市反演精度更高，在地形起伏度较大区域精度略低。

3.3 喀斯特地区各地类降尺度精度评价

为了更清楚地显示喀斯特地区局部降尺度成果，分别从区域a和区域b 4种地类(建设用地、植被、裸土、水体)中截取最具代表性的局部进行对比(图6-图9，彩图见附录2)，可以看出3种降尺度方法在不同地类区域的准确性不同，但总体上KRF方法在4种地类上的表现均优于其他算法。TsHARP方法仅在同质的植被区表现较好[18]，在其余地类的LST结果中均出现低估现象；MTVRF方法引入了较多的尺度因子，虽然在水体、植被区域表现较好，但在建设用地和裸土上表现较差，与Wu等[20]的研究结果不同，这可能是因为喀斯特地区建设用地和裸土分布较为破碎，导致这两个区域与其他地物的交界处出现异常值。

进一步统计4种地类的评价指标(表3)，可以看出：KRF方法的MAE比MTVRF模型和TsHARP算法分别降低了0.2069～0.4907 K和0.3596～3.6282 K，RMSE比MTVRF模型和TsHARP算法分别降低了0.2818～0.7051 K和0.4129～4.184 K，R2比MTVRF模型和TsHARP算法分别提高了0.1014～0.1965和0.1329～0.4688，说明本文方法在4种地类中的精度更高；另外，3种方法在植被和水体区域效果较好，但在裸土和城镇区域出现较大偏差，这可能是因为裸土和城镇区域异质性较强，说明精度与地表异质性相关[32]。

图6 喀斯特地区水体降尺度结果比较

图7 喀斯特地区植被降尺度结果比较

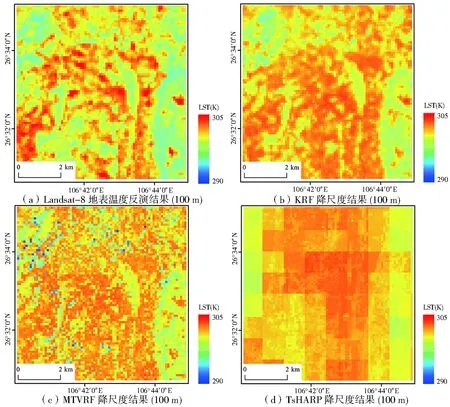
图8 喀斯特地区建设用地降尺度结果比较

图9 喀斯特地区裸土降尺度结果比较

表3 3种方法在4种地类的降尺度结果精度

4 结论

本文从热红外辐射亮度出发，针对喀斯特地区的特征，添加合适的尺度因子，利用RF模型将空间分辨率为1 km的MODIS 第31、32波段辐射亮度降尺度至100 m，通过劈窗算法对100 m的热红外辐射亮度进行反演，最终构建了适合喀斯特地区的随机森林(KRF)模型，实现了喀斯特地区的地表温度空间降尺度。从喀斯特地区起伏度不同的两个区域和4种不同地类两种尺度上，将本文方法与MTVRF模型、TsHARP算法进行对比，得到如下结论：1)在不同起伏度的两个喀斯特地区，本文方法均能较好地模拟LST的热特征，且更适用于喀斯特地形变化较为平缓的山区城市。2)在不同地类降尺度方面，本文方法表现最好，特别是添加了BSI、BRp和高程因子与热辐射亮度的降尺度研究，拓展了传统降尺度模型的应用范围，显著提高了喀斯特地区各地类的降尺度效果。整体而言，本文方法较MTVRF模型和TsHARP算法在定性和定量上都得到明显改善，能有效提高喀斯特地区地表温度空间分辨率，但针对地形变化更大、异质性较强的区域，降尺度结果还有改进的空间。