基于NSCT与改进SIFT特征点的GF-2影像水印算法

马 文 骏，张 黎 明，李 玉，秦 如 贞

(兰州交通大学测绘与地理信息学院，甘肃 兰州 730070；地理国情监测技术应用国家地方联合工程研究中心，甘肃 兰州 730070；甘肃省地理国情监测工程实验室，甘肃 兰州 730070)

0 引言

高分二号(GF-2)卫星作为对地观测系统中首颗突破亚米级分辨率的卫星，其成功发射与使用标志高分辨率影像的国产化，降低了对国外高分辨率数据的依赖性[1，2]。GF-2影像具有分辨率和精度高、应用领域广等特点，但在发达的网络环境中会出现数据泄露、盗版及非法传播等安全问题，难以保证影像数据的安全[3]。数字水印作为一种信息安全领域的新技术，可为GF-2影像数据的安全使用提供技术保障。然而，在实际应用中需对GF-2影像进行拼接、裁剪、平移、旋转等处理，使得常用的图像水印算法因鲁棒性差、水印同步问题而无法满足GF-2影像版权保护需求[4]。例如：任娜等提出一种使用密钥矩阵和模板匹配的空间域半盲水印算法，该算法不可见性良好，在受到裁剪、旋转等攻击后能够提取出较为完整的水印信息[5]，但应用于GF-2影像时，易受到攻击者的恶意破坏，从而失去对GF-2影像的版权保护作用；林威等针对瓦片遥感影像数据，提出一种基于快速响应矩阵码(Quick Response code,QR code)的数字水印算法，即对QR码水印图像进行数据压缩和预处理，并通过水印嵌入单元和水印信息位之间建立的映射关系实现水印嵌入，有效提升了水印信息容量，并对于常规图像处理操作和拼接攻击具备良好的保真度和鲁棒性[6]，但对于裁切攻击的鲁棒性不足，无法满足GF-2影像抗几何攻击的要求。因此，如何抵抗几何攻击是GF-2影像水印算法需要攻克的重要难题。

目前，广泛使用的抗几何攻击水印算法大致可分为4类[7，8]：1)扩频调制方法，是最常见的水印嵌入方法，通过加性或乘性扩频方式嵌入水印信息，对常见的图像操作以及部分几何攻击具有较强的鲁棒性[9]，但对原始图像产生的干扰效应会导致水印解码性能下降[10]；2)模板插入方法，是一种常见的再同步技术，可将反映图像几何变换参数的模板嵌入图像中，用作补偿几何变形的参考，从而达到抗几何攻击的目的[11]，可有效解决含水印图像遭到几何攻击后的同步问题，但易被攻击方检测并移除，从而剥夺其抗几何攻击的能力[12]；3)不变域水印算法，能有效抵抗几何攻击，可通过Fourier Mellin变换(FMT)[13]、拉东变换[14]、奇异值分解(Singular Value Decomposition，SVD)[15]等方法得到图像的几何不变域并嵌入水印信息，从而提高对旋转、缩放等几何攻击的鲁棒性[16，17]，但该算法复杂度较高，对原始数据的精确性影响较大[18]。以上3种方法仅凭像素值或不变域系数实现水印嵌入，未顾及载体图像自身的特点。4)基于特征点的水印同步方法，通过稳定的图像特征点标识出水印嵌入位置，并将水印嵌入所选取特征点构建的特征区域中，利用特征点定位嵌入区域并提取水印信息，对几何攻击具有更好的鲁棒性[19，20]。与其他特征点提取算法相比，尺度不变特征变换(Scale-Invariant Feature Transform，SIFT)特征点及其构建的特征区域性能更佳。GF-2影像数据量大、地物信息丰富，提取的SIFT特征点具有多量性，利用SIFT特征点构建特征区域时，会出现严重的区域重叠现象，使得水印嵌入域选择困难，水印容量不足，严重影响该水印方法的鲁棒性与效率。变换域水印算法相比频域水印算法具有更好的不可见性与鲁棒性，其中，非下采样轮廓波变换(Non-Subsampled Contourlet Transform，NSCT)是一种多尺度、多方向、平移不变且能快速实现的变换，可避免频谱混叠现象，更好地表达影像内容，已被应用于数字水印研究中[21]。

综上，目前对于普通遥感影像的抗几何攻击水印算法已有一定的研究基础，但均未考虑数据的特性，应用于GF-2影像的版权保护时，仍存在安全性与抗几何攻击鲁棒性不足等问题。因此，本文结合已改进SIFT特征点的特征区域构建思想与变化域水印方案，提出一种基于NSCT与改进SIFT特征点的GF-2影像水印算法。

1 研究方法

本文选用两幅满足人类视觉系统的红、绿、蓝3波段合成的GF-2影像数据(图1)，并对数据进行辐射校正、几何校正、图像融合等预处理。GF-2影像水印算法流程(图2)为：首先利用Mean Shift方法改进SIFT算法，优化并保留性质稳定、数量适宜的GF-2影像SIFT特征点；然后利用几何归一化技术构建具有旋转不变性的SIFT特征区域，选取特征区域并经NSCT变换分解得出低频子带；设计SVD水印嵌入机制，将经过Arnold变换的水印信息嵌入其中；最后通过逆变换得到含水印影像。

图1 GF-2影像数据

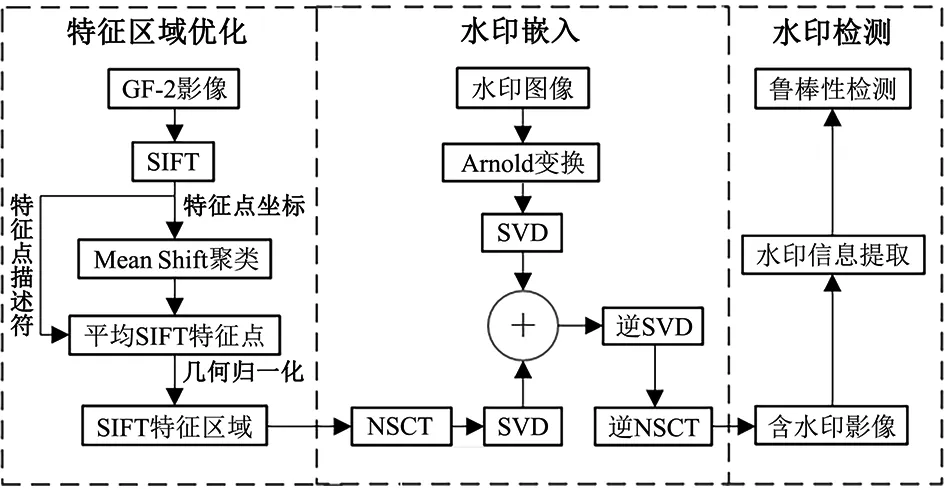
图2 算法流程

1.1 SIFT特征点提取

SIFT将图像与高斯函数卷积，构成高斯差分空间(Difference of Gaussian，DoG)，若DoG中存在某点的像素值是其相同或相邻DoG中的极值(最大值或最小值)，则确定该点为图像的一个SIFT特征点[22]。

鉴于SIFT特征点对图像缩放、旋转、平移、亮度变化和射影变换等操作具有不变性，其在高分影像数字水印技术中也具备可行性，因此，本文算法利用SIFT算子提取GF-2影像的SIFT特征点。具体步骤为：1)构建DoG，检测尺度空间中的极值点；2)通过对极值点进行三位二次函数拟合，精确得到极值点的尺度与空间位置，并将其作为特征点；3)根据特征点邻域像素的梯度方向分布特性确定极值点的方向参数；4)生成特征点描述符，得到GF-2影像的SIFT特征点。

1.2 基于Mean Shift的特征点筛选

GF-2影像地物信息丰富、数据量大，提取的SIFT特征点数量繁多，不利于后续特征区域的构建，故需对特征点进行适当筛选。Mean Shift算法是一种非参数的概率密度梯度估计算法[23]，聚类效率高，对GF-2影像SIFT特征点的优化处理具有可行性，已成功应用于数字水印研究[24]，因此，本文选择该算法对提取的SIFT特征点进行筛选与优化处理。Mean Shift聚类过程为：1)对于给定样本x，样本点为xi(i=1,2,…,n)，计算x的Mean Shift向量mh,G(x)(式(1))；2)对各样本点xi进行Mean Shift迭代，直到收敛，即当mh,G(xi)=0时，得到稳定的参考点，具体过程如式(2)所示；3)将该参考点作为中心进行聚类，该过程中输入的样本点将归类到稳定参考点所在的类别中；4)当任意两个类别的聚类中心距离小于阈值时，将其合并，否则聚类结束[25]。

(1)

式中：g(·)为核函数的导数；h为内核半径[26]。

xj=xi+mh,G(xi)

(2)

式中：xj(j=1,…,n)为迭代后得到的稳定参考点。

本文算法以提取到的SIFT特征点坐标作为样本值，通过Mean Shift聚类后，为同一类别中的关键点计算平均SIFT描述符，公式为：

(3)

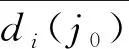
1.3 SIFT几何不变特征区域的确定

由于SIFT特征点具有多量性，若选取的特征点尺度过小，会导致几何攻击后无法成功检测到水印信息，尺度过大则会导致特征区域发生重叠，鲁棒性变差，因此，进一步对特征点的间距D进行筛选，公式为：

D≥(M+N)/k

(4)

式中：M、N分别为影像宽度与高度；k为常数，本文取k=20。

由于圆形区域具有旋转不变性，且在定位时仅需唯一的特征点，故本文算法对经过筛选后的SIFT特征点，在确定其位置(x′,y′)、方向θ0、尺度S后，以R为半径构建圆形区域：

(x-x′)2+(y-y′)2=(RS)2

(5)

将所得圆形特征区域周围补0，构建外接矩形图像，并对矩形图像进行归一化操作，以减小几何变换对图像的影响。本文算法将除去归一化图像四周黑色区域的圆形区域作为水印嵌入区域，其圆心为归一化图像的几何中心。为便于在变化域中进行水印嵌入操作，将圆形区域坐标转化为极坐标，公式如下：

(6)

(7)

式中：(x,y)为圆形区域的平面直角坐标；(ρ,θ)为圆形区域的极坐标；(x1,y1)为矩形区域的平面直角坐标；ζ0为常数，本文取ζ0=0，当ζ0≠0时，式(7)可将圆形映射到矩形。

1.4 基于NSCT的水印算法

1.4.1 NSCT变换 NSCT继承了Contourlet多尺度几何变换的优良特性，表示图像不同方向上的平滑轮廓时，比Contourlet变换和离散小波变换更有效，被广泛应用于图像增强[27]、图像融合[28]、数字水印[29]等领域。NSCT由非下采样塔形滤波器(Non-Subsampled Pyramid，NSP)和非采样方向性滤波器组(Non-Subsampled Directional Filter Banks，NSDFB)构成(图3)，NSP保证了多尺度性，NSDFB保证了多方向性。这两组滤波器均为双通道滤波器组，没有上、下采样操作，因此，NSCT具有平移不变性、多尺度性、多方向性和高效性，故本文将其与SVD结合以获得更多的系数嵌入水印。

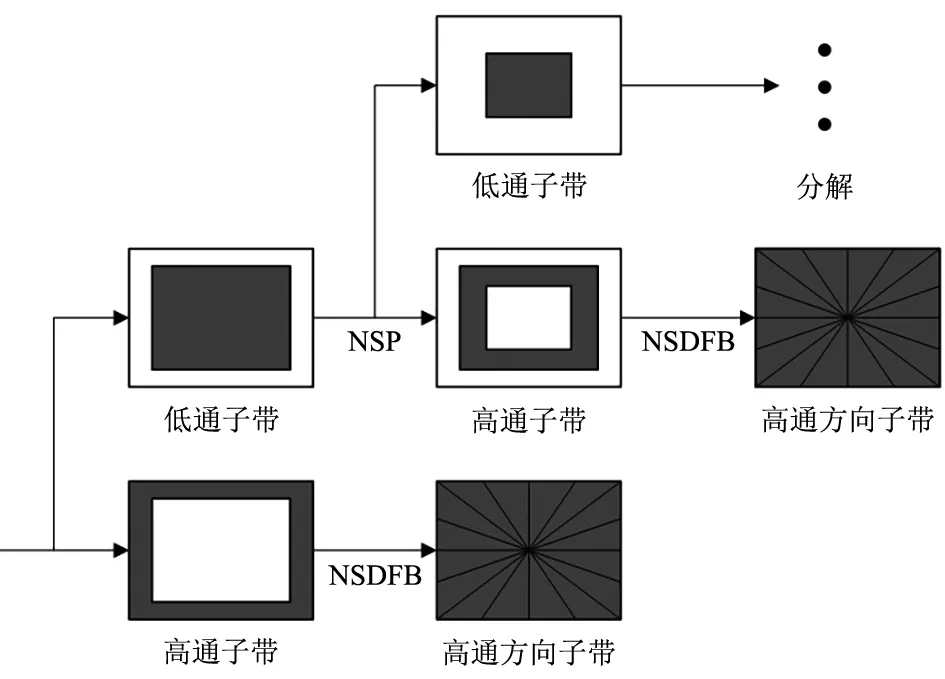
图3 NSCT原理示意

1.4.2 水印信息生成 鉴于GF-2影像的解译需求，嵌入水印时不能影响其空间相关性，因此，本文选择Arnold变换方法，对原始水印信息空间域中各像素点的位置进行置换，破坏水印图像的相关性，以达到对原始水印加密的目的，提高嵌入水印的安全性。Arnold变换周期为T，若进行T/2次变换，水印图像置乱度最大且鲁棒性最强；当进行T次变换后，重新得到原始水印图像。具体定义为：

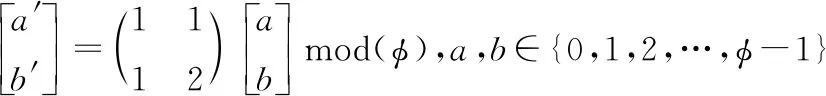
(8)

式中：(a,b)为原始水印图像中的像素点坐标；(a′,b′)为变换后像素点坐标；mod(·)是取模运算；φ为水印图像矩阵的阶数。

1.4.3 水印嵌入 NSCT变换提取的子带信息中含有相对高分量引起的模糊纹理，因此，本文算法利用SVD分解建立特征区域在NSCT域的奇异值矩阵，在保证GF-2影像质量的前提下，尽可能增大水印的嵌入强度；同时结合SIFT特征区域抗几何攻击的特点，显著提高水印算法的鲁棒性。水印嵌入步骤(图4)为：1)读取原始数据，选取的GF-2影像尺寸为M×N；2)读取二值水印信息W0，依据式(8)对W0进行Arnold置乱，得到水印信息W，图幅尺寸为Z×L，保存变换次数为密钥K1；3)对影像进行SIFT特征点提取，利用Mean Shift聚类并构建适于水印嵌入的特征区域，保留聚类后特征点的坐标信息为密钥K2；4)对所确定特征区域进行NSCT分解，得到低频子带L0；5)利用式(9)对L0、W进行SVD分解，得到E0、EW中的奇异值λ0、λW(保存U0、V0、UW与VW为密钥K3)；6)依据式(10)将奇异值λW嵌入低频子带L0的奇异值λ0中，得到已嵌入水印信息奇异值的低频子带奇异值λL′，并进行逆SVD得到L1；7)对低频子带L1进行逆NSCT变换，还原为所选SIFT特征区域，并得到含水印影像。

图4 水印嵌入过程

(9)

式中：E0、EW为奇异值矩阵；U0、UW为左奇异矩阵；V0、VW为右奇异矩阵。

λL′=λ0+αλW

(10)

式中：α为水印强度。

1.4.4 水印提取 水印的提取过程即为嵌入的逆过程，步骤(图5)为：1)读取含水印影像与原始影像，对两种影像进行SIFT特征点提取，并依据密钥K2确定特征区域；2)对所确定特征区域进行NSCT分解，得到低频子带L1，并用SVD提取其奇异值λL′和λ0；3)利用式(11)得到水印信息奇异值λW，并通过密钥K3逆SVD得到未解密的水印信息W；4)根据保存的密钥K1确定Arnold变换次数，而后对提取的水印信息进行Arnold变换，得到水印信息W0。

图5 水印提取过程

λW=(λL′-λ0)/α

(11)

2 实验与分析

利用SIFT算子对GF-2影像(图1)进行特征点提取，所得结果(图6a、图6b)中特征点数量繁多且分布密集，无法构建合理且适宜的特征区域。通过Mean Shift方法对提取的SIFT特征点进行聚类优化，所得结果(图6c、图6d)中SIFT特征点数量适宜，为后续构建SIFT特征区域以及在NSCT域中嵌入水印提供了保障。

图6 SIFT特征点及优化后的SIFT特征点

2.1 不可见性检测

通过不可见性检测检验本文算法的性能，并与文献[29]中NSCT与SVD相结合的水印信息嵌入算法进行对比。利用两种算法分别在图1的两幅GF-2影像中嵌入水印信息，可见本文算法结果(图7a、图7c)与文献[29]算法结果(图7b、图7d)在主观视觉评价标准下，与原始影像相比，道路、建筑物等地物信息并无肉眼可辨的差异。因此，为客观检验本文算法的不可见性，还需进行定量对比分析。

采用峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)作为水印不可见性定量评估指标(式(12))，其值越高，说明水印的不可见性定量越好。由表1可知，本文算法含水印影像的PSNR值均高于42，明显高于文献[29]算法的PSNR值。综上，本文算法融合了SIFT与NSCT变换域方法的优点，故而含水印影像的视觉效果良好，PSNR值较高，说明嵌入水印后影像质量未受到明显影响，从客观、定量角度验证了本文算法的有效性与水印的不可见性。

(12)

图7 含水印影像对比

式中：Q0(i,j)与Q1(i,j)分别为原始影像与含水印影像在(i,j)处的像元值；M、N为影像尺寸。

表1 水印不可见性评估结果

2.2 鲁棒性检测

算法鲁棒性一般用归一化相关系数(Normalized Correlation，NC)作为评价指标(式(13))，NC值越接近1，说明提取的水印与原始水印越相似。

(13)

式中：W(i,j)、W′(i,j)分别表示原始水印和提取的水印；Z×L表示提取的水印图像尺寸;XNOR表示异或非运算。

本次实验通过对嵌入水印后的影像进行椒盐噪声、低通滤波等攻击，检验本文算法对常规攻击的鲁棒性。由表2可知，经过以上常规攻击后，本文算法的NC值均接近1，在JPEG压缩与直方图均衡攻击后的NC值均高于文献[29]算法的NC值，表明本文算法鲁棒性良好，能抵抗多种常规影像攻击。

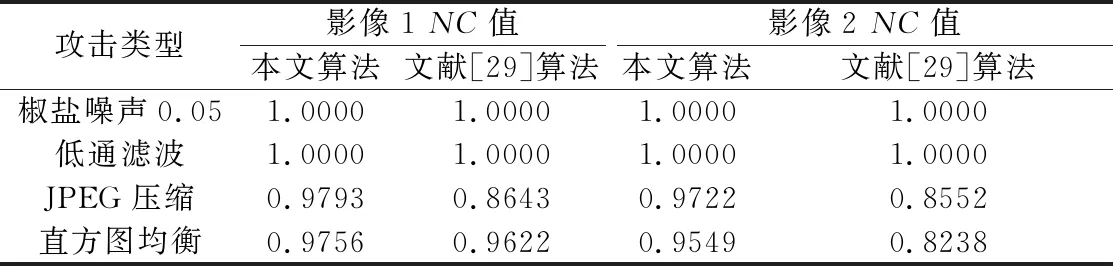
表2 常规攻击后的相关系数

进一步采用裁切、旋转、缩放几何攻击对嵌入水印后的影像进行鲁棒性测试，并与文献[29]、文献[30]算法结果相对比(表3)，其中文献[30]算法利用QR码生成水印信息，并将其嵌入载体影像经离散余弦变换后的直流系数中。由表3可以看出，本文算法在经过多种几何攻击后，提取的水印信息与原始水印信息几乎无差异，相对于裁切攻击，仅需保留一个特征区域就能实现水印的提取操作，所得结果的NC值均大于0.9，虽稍逊于文献[30]算法的结果，但均可以提取出水印信息。此外，本文算法在经过旋转、缩放攻击后，提取的水印信息与原始水印信息的NC值都接近1，效果均优于其他两种算法，说明本文算法具有良好的鲁棒性。

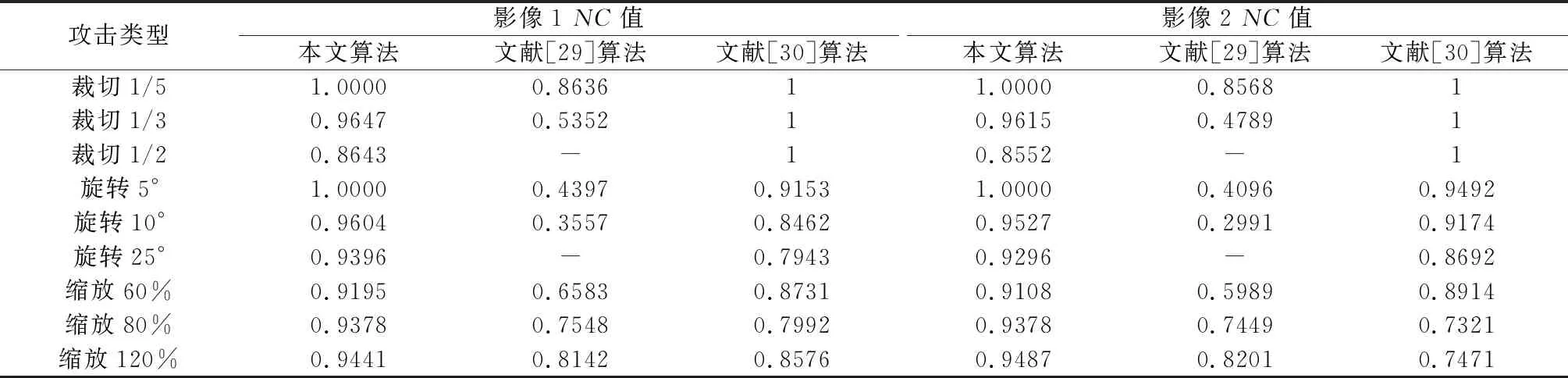
表3 几何攻击后的相关系数

3 结语

本文通过Mean Shift聚类算法对GF-2影像提取的特征点进行筛选与过滤，构建矩形特征区域并以此为水印嵌入位置，结合NSCT对影像良好的细节保留性与方向性以及SVD对影像优异的稳定性，提出一种适用于GF-2影像的抗几何攻击水印算法。该算法对SIFT特征点进行合理筛选，消除了特征区域的重叠现象，提高了算法抗几何攻击的鲁棒性；将水印信息嵌入特征区域NSCT域中，使算法亦可较好地抵御常规信号处理。实验结果表明，本文算法在保证水印不可见性的前提下，对常规几何攻击具有较高的鲁棒性，因此，可用于对GF-2影像与其他常规遥感影像的版权保护，为遥感影像的数据安全问题提供了一种切实可行的解决途径。然而，本文算法在进行水印检测与提取时，需借助密钥搜索含水印特征区域，未能实现水印的盲提取，今后将考虑采用一种自适应的特征区域水印嵌入算法。