基于遗传算法优化BP神经网络的土壤盐渍化反演
2021-04-15杨练兵,郑宏伟,4*,罗格平,4,杨辽,4
杨 练 兵,郑 宏 伟,4*,罗 格 平,4,杨 辽,4
(1.中国科学院新疆生态与地理研究所荒漠与绿洲国家重点实验室,新疆 乌鲁木齐 830011;2.新疆维吾尔自治区遥感与地理信息系统应用重点实验室,新疆 乌鲁木齐 830011;3.中国科学院大学,北京 100049;4.中国科学院中亚生态与环境研究中心,新疆 乌鲁木齐 830011)
0 引言
土壤盐渍化是土地退化和荒漠化的主要类型之一,其分布范围广,危害时间长,严重制约着干旱区农业生产,已成为全球性生态环境问题[1]。卫星遥感数据能宏观、动态地监测土壤盐渍化信息[2],相关研究经历了定性分类和定量反演两个阶段。在定量反演方面,众多学者对获得的遥感数据和非遥感数据进行数学变换以构建反演参数,并结合采样点土壤盐分含量(Soil Salinity Content,SSC)数据建立相应的反演模型,以获得大范围的土壤盐分含量。
受自然条件和人类活动方式的影响,土壤盐渍化成因复杂[3],光谱波段、植被指数、盐分指数、下垫面参数、特征空间、地形参数、物候特征等都被作为反演土壤盐分含量的参数[4,5]。相关研究采用多元线性回归(MLR)、偏最小二乘回归(PLSR)、地理加权回归(GWR)、分位数回归(QR)等线性模型拟合反演参数与土壤盐分含量的关系[6-8]。由于多数反演参数与土壤盐分含量之间存在非线性关系[9],BP神经网络(BPNN)、支持向量机(SVM)、多元自适应回归样条(MARS)、随机森林(RF)等非线性模型也被用于反演土壤盐分含量[10-14]。由于部分机器学习算法自身没有特征优选的能力,皮尔森相关分析[15,16]、最佳指数法[17]、灰色关联分析[18]等过滤方法被用于筛选反演参数子集,这种特征筛选方式减少了信息冗余,但难以获得最佳反演参数子集;同时,机器学习模型的参数影响算法的预测精度、运算速度和稳健性,已有研究多通过经验方法选取模型参数,调参效率低且难以获得最优参数;另外,应用于土壤盐渍化反演的机器学习模型种类较多,以往多关注不同模型间的对比,对同一模型的优化改进较少研究。
BPNN具有优良的非线性逼近能力,是较早引入土壤盐渍化反演的机器学习模型[13],但其预测精度受结构参数和初始权重的影响[19]。为此,本研究建立3组优化模型:先利用遗传算法(GA)同步优化输入层反演参数子集和隐含层神经元数量,再优化初始权重的BPNN(GA-BP)模型;将变量投影重要性(VIP)算法分割阈值分别设为1和0.5,优化出两组输入层反演参数子集,并将其分别代入GA优化隐含层神经元数量,再优化初始权重的BPNN (VIP1-GA-BP、VIP2-GA-BP)模型。在新疆玛纳斯流域和三工河流域各选一靶区,基于谷歌地球引擎(GEE)平台构建反演参数,对比分析两靶区3组优化模型的反演精度,并统计各类盐渍土的面积比例,以期为土壤盐渍化信息的高效获取提供支持。
1 研究区与数据
1.1 研究区概况
玛纳斯流域(85°01′~86°32′E,43°27′~45°21′N)位于天山北麓(图1a)、准噶尔盆地南缘,由玛纳斯河、塔西河、宁家河、金沟河、巴音沟河和大南沟河组成,流域面积为3.35×104km2,地势东南高、西北低,高程为256~5 242 m,有典型的山地—绿洲—荒漠系统。该流域深居内陆干旱区,气候干燥,光照充足,年均气温 5~7 ℃,年降水量110~200 mm,年蒸发量1 500~2 000 mm[20],水资源主要来源于冰雪融水和高山降水,农业生产起初的大水漫灌引发严重的土壤盐渍化问题,改为滴灌后土壤盐渍化程度有所减轻[21]。
三工河流域(87°47′~88°17′E,43°09′~45°29′N)位于天山北麓中段东部(图1b)、准噶尔盆地南缘,主要由水磨沟河、三工河和四工河组成,流域面积为1.67×103km2,总人口约为11万人[22],高程为480~650 m,地势由东南向西北倾斜。该流域降水稀少(约220 mm/a),蒸发量大(约1 399 mm/a),年均温约为7.3 ℃[23],以种植业为主,灌区水资源主要来源于冰雪融水,地下水矿化度高,地下水位抬升及强烈的蒸发作用容易导致地表积盐[24]。
1.2 采样点数据
2016年7-8月,在玛纳斯流域和三工河流域各选一靶区,用手持RTK-GPS进行采样点定位,采样点考虑不同的植被覆盖、地貌类型和交通可达性,具有一定的代表性。在两靶区环境因素相似的区域设置30 m×30 m样方,在样方内按照“五点采样法”采集土壤样品,采样深度为 0~20 cm;采集的土壤样品经过自然风干、磨碎、过筛后,测定八大离子(Ca2+,Mg2+,K+,Na+,CO32-,HCO3-,Cl-,SO42-)的含量,对其求和获得土壤样品盐分含量(SSC),将样方内土壤样品的SSC均值作为实际观测值。针对测量结果中的误差,基于箱线图分析用四分位差(IQR)检测异常值点,最终在玛纳斯和三工河靶区获得可用采样点数量分别为97个和119个(图1)。

图1 两靶区样点分布
在玛纳斯靶区和三工河靶区分别随机选取总样本集的26.80%和26.05%(约1/4)作为测试集,其余样本数据作为建模集。由总样本集、建模集、测试集的描述性统计特征(表1)可知:两靶区总样本集的均值和变异系数均介于建模集与测试集之间,表明两靶区建模集和测试集样本数据的范围相对一致,一定程度上避免了模型构建和验证中的偏差估计[25]。假设样本数据能代替总体,按照变异系数(CV)评价准则[26],两靶区SSC均属于中等变异;按照新疆盐碱土标准[27],从均值看,玛纳斯靶区和三工河靶区土壤分别属于重度盐渍化和中度盐渍化。

表1 两靶区采样点SSC统计描述
1.3 影像数据与反演参数
谷歌地球引擎(GEE)是目前较为成熟的遥感大数据分析云平台[28],可提供高性能并行计算服务。本研究参考相关文献,调用GEE平台中预处理好的Landsat-8 OLI影像数据(空间分辨率30 m)、Sentinel-1 SAR影像数据(空间分辨率5 m×20 m)及SRTM高程数据(空间分辨率30 m)计算出两靶区的52个反演参数(表2),并将广义差分植被指数(GDVI)、土壤调节植被指数(SAVI)、增强植被指数(EVI)、绿色大气阻抗指数(GARI)的反演参数设为经验值;考虑到Landsat-8 OLI各波段的分辨率和特性,只选取可能对土壤盐渍化具有表征能力的可见光、近红外和短波红外波段作为反演参数。由于本研究SSC采样点数据来源于30 m×30 m样方,故通过三次卷积内插将反演参数空间分辨率统一到30 m。为接近SSC采样时间且满足靶区范围内无云的条件,选取玛纳斯靶区和三工河靶区成像时间分别为2016年8月4日和8月29日的Landsat-8 OLI数据以及2016年8月2日和8月26日的Sentinel-1 SAR数据;SRTM高程数据制作时间为2000年2月。

表2 SSC反演参数
2 研究方法
本研究基于BP神经网络(BPNN),通过遗传算法(GA)、变量投影重要性(VIP)算法共设计出3组优化的BPNN模型,具体研究流程(图2)为:1)先利用GA同步优化输入层反演参数子集和隐含层神经元数量,再优化初始权重的BPNN(GA-BP)模型;2)将VIP算法分割阈值分别设为1和0.5,优化出两组输入层反演参数子集,将两组输入层反演参数子集分别代入GA,先优化隐含层神经元数量,再优化初始权重的BPNN(VIP1-GA-BP、VIP2-GA-BP) 模型;3)对两靶区3组模型反演SSC的精度、空间分布、筛选的反演参数进行对比,并统计各类盐渍土的面积比例。
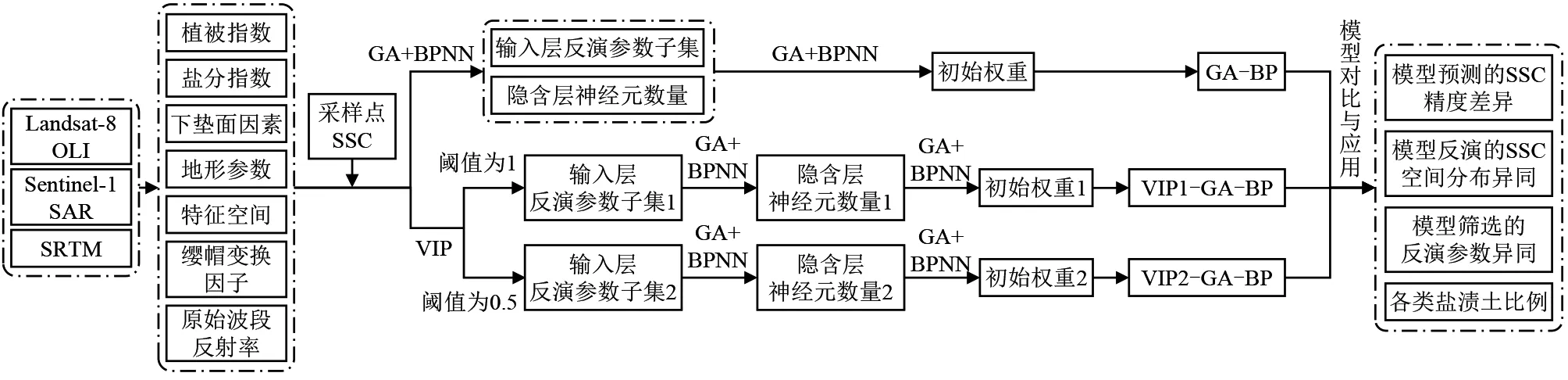
图2 模型设计流程及研究内容
2.1 遗传算法(GA)优化的BP神经网络(GA-BP)
GA是一种模拟生物进化过程的启发式算法[40],其将可能的解转换为种群中个体的染色体(用二进制、实数、十进制、格雷、符号等编码方式以符号串形式表示),染色体的基因位取值区间需根据具体问题设定;GA有选择、交叉、变异3种遗传操作算子,以适应度函数为评价指标,通过遗传操作算子不断更新种群,解码最终种群中适应度值最高个体的染色体为问题的最优解。GA-BP结构参数染色体(图3)中,im(m=1,…,n,n为待筛选反演参数的数量)代表输入层神经元的基因位,取值为1(表示对应的反演参数参与建模)或0(表示反演参数不参与建模);h表示隐含层神经元数量的基因位。本研究采用两阶段方式构建GA-BP:先用GA对BPNN的结构参数进行优化,然后对BPNN的初始权重进行优化。

图3 结构参数染色体示意
(1)BPNN结构参数的优化。BPNN包括输入层、隐含层、输出层3层网络结构[41],基本组成单位为神经元,通过在隐含层和输出层设置激活函数解决非线性拟合问题。当BPNN仅含一个隐含层且隐含层神经元数量较多时,其具备很强的函数逼近或映射能力[42],故本研究用于SSC预测的BPNN只设一个隐含层(图4)。本文中BPNN结构参数为输入层神经元(输入层反演参数子集)、隐含层神经元数量和输出层神经元数量,由于输出层神经元数量为1,故只需对输入层反演参数子集和隐含层神经元数量进行优化。BPNN隐含层神经元数量与输入层神经元数量有关[43],而GA-BP各结构参数染色体代表的输入层神经元数量不同,故隐含层神经元数量的基因位取值区间需动态更改,研究中依据经验公式(式(1)-式(3)[43]、式(4)[44])联立取最大值和最小值确定。为实现隐含层神经元数量基因位取值区间的动态更新,本研究在GA-BP中对结构参数染色体的交叉算子和变异算子进行改进:在结构参数染色体进行交叉和变异运算时,先对输入层神经元基因进行运算;然后根据其代表的神经元数量,推导出隐含层神经元数量的基因位取值区间;最后在该取值区间中随机生成一整数并将其作为隐含层神经元数量的基因位数值。通过遗传算子不断更新BPNN结构参数种群,解码最终结构参数种群中适应度值最高个体的染色体,即可获得最优的结构参数(图5)。
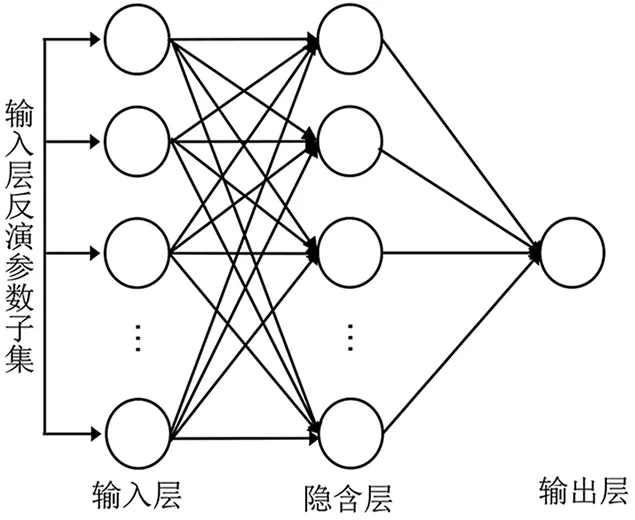
图4 BPNN结构图示
(1)
p=2n+1
(2)
p=log2n
(3)
(4)
式中:p、m、n分别为隐含层、输出层、输入层的神经元数量;q用于调整隐含层神经元数量,取值范围为1~10之间的整数。

图5 GA优化BPNN结构参数示意
(2)BPNN初始权重的优化。初始权重染色体如图6所示,wp(p=1,…,q,q为初始权重数量)代表初始权重的基因位。确定BPNN最优的输入层反演参数子集和隐含层神经元数量后,利用GA的遗传算子不断更新初始权重种群,解码最终初始权重种群中适应度值最高个体的染色体,即可获得最优的初始权重(图7)。

图6 初始权重染色体示意
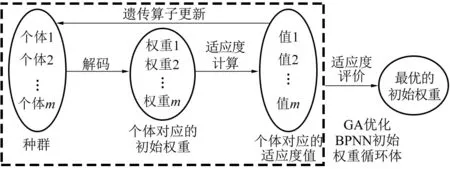
图7 GA优化BPNN初始权重示意
2.2 变量投影重要性(VIP)算法
VIP算法是基于偏最小二乘回归的特征筛选方法,可评价自变量对因变量集合的解释能力,公式为:
(5)
式中:k为自变量数量;th为从自变量集合X=(x1,x2,…,xj,…,xk)中提取的主成分;Y为因变量集合;whj用于衡量自变量xj对th的边际贡献;Rd(Y;th)为th对Y的解释能力,Rd(Y;t1,t2,…,tm)为t1,t2,…,tm对Y的累积解释能力。VIPj大于1,表示xj对Y非常重要;VIPj在0.5~1之间,表示xj对Y的重要性不明确,需要根据其他条件进行判断或增加样本;VIPj小于0.5,表示xj对Y不重要[45]。
VIP1-GA-BP和VIP2-GA-BP的建模流程(略)与GA-BP相似,区别为: GA-BP中输入层反演参数子集和隐含层神经元数量的优化同步进行,而VIP1-GA-BP和VIP2-GA-BP对这两者的优化是分开进行的。
2.3 精度检验指标
本研究采用均方根误差(RMSE)、平均绝对百分误差(MAPE)和相对分析误差预测偏差(RPD)对模型性能进行评价,各指标的计算公式如式(6)-式(8)所示。RMSE越小,表示模型的预测精度越高;MAPE越接近于0,表明模型预测的相对误差越小;RPD<1.4,说明模型不可靠,1.4
(6)
(7)
RPD=SD/RMSE
(8)
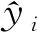
3 反演参数筛选及模型参数设置
在两靶区以建模集及其对应的反演参数为数据源,基于SIMCA软件进行VIP分析;根据VIP值对解释变量的重要性意义,设置分割阈值为1和0.5,将VIP值大于或等于1的反演参数集记为A组,大于或等于0.5的记为B组(图8)。在5%的显著性水平上,玛纳斯靶区共有22个反演参数的VIP值大于1(包含三工河靶区VIP值大于1的反演参数),13个在0.5~1之间;三工河靶区反演参数的VIP值均大于0.5,13个大于1。
本研究采用MATLAB遗传算法工具箱(GAOT)设计GA,GA的编码方式为实数编码,建立优化的BPNN模型时,将测试集样本数据平均绝对误差的倒数作为GA优化BPNN结构参数(GA 对VIP1-GA-BP、VIP2-GA-BP优化的结构参数均仅为隐含层神经元数量)和BPNN初始权重的适应度函数。两靶区3组模型的BPNN训练次数均设为1 000,训练目标设为0.02,学习速率设为0.03,初始权重基因位取值范围设为-1~1。为避免各维度数据间数量级的差别,两靶区训练集和测试集及其对应的反演参数数值均归一化至0~1之间。tansig能将数值映射到-1~1之间,便于BPNN对输入和输出数据的非线性拟合,logsig能将输出数值映射到0~1之间,便于BPNN后续的反归一化处理,故将两靶区3组模型的BPNN隐含层神经元激活函数均设为tansig,将BPNN输出层神经元激活函数均设为logsig。
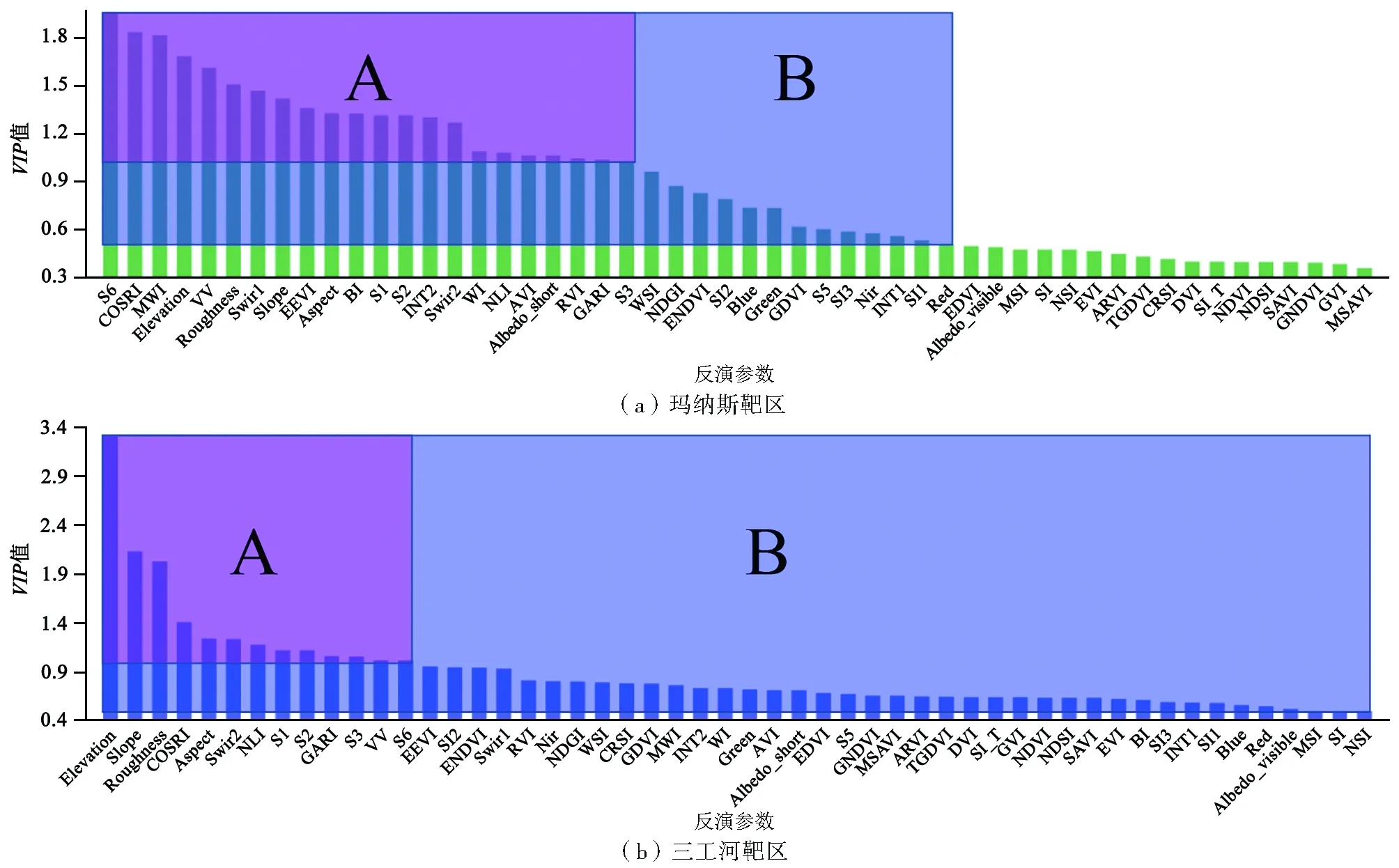
图8 SSC反演参数变量投影重要性排序
4 结果分析
4.1 模型的预测精度和反演参数
随着GA优化BPNN结构参数的进化代数逐步增加,两靶区各组模型种群中个体适应度值也逐渐增大,最后趋于稳定(图9);两靶区最优适应度值从大到小排序分别为GA-BP>VIP2-GA-BP>VIP1-GA-BP和GA-BP>VIP1-GA-BP>VIP2-GA-BP,可见VIP1-GA-BP、VIP2-GA-BP最优适应度值之间的差值均较小。

图9 GA优化BPNN结构参数的最佳适应度曲线
对两靶区各组模型最终结构参数种群中适应度值最高个体的染色体进行解码,确定VIP1-GA-BP、VIP2-GA-BP的隐含层神经元数量及GA-BP的输入层反演参数子集(C组反演参数)和隐含层神经元数量,两靶区VIP分析确定的A组、B组反演参数分别作为VIP1-GA-BP和VIP2-GA-BP的输入层反演参数子集;之后采用GA对初始权重进行优化,建立3组优化的BPNN模型。由两靶区3组模型的SSC反演精度(表3)可以看出:玛纳斯靶区3组模型建模集间RMSE、MAPE的差异均较小,而测试集间的差异均较大,其中GA-BP模型在测试集上的RMSE和MAPE均最小(分别为11.56 g/kg、32.78%)、RPD最大(1.64),表明GA-BP模型的反演精度最高;在三工河靶区,GA-BP模型的反演精度也最高,其RMSE、MAPE、RPD分别为3.60 g/kg、 25.21%、1.47。综上,3组模型反演精度由高至低依次为GA-BP、VIP1-GA-BP、VIP2-GA-BP。由VIP算法原理可知,B组比A组多出的反演参数对被解释变量SSC的重要性不明确,信噪比较小,会造成VIP2-GA-BP较严重的过拟合,一定程度上解释了两靶区VIP1-GA-BP的反演精度均高于VIP2-GA-BP。GA-BP同步筛选了反演参数子集和隐含层神经元数量,考虑了反演参数之间及反演参数与反演模型间的相互关系,最终筛选的反演参数子集与BPNN耦合性高;而VIP算法虽对反演参数进行重要性排序,但未考虑参数间的相互关系及反演SSC的特定建模方法[46],故两靶区GA-BP的反演精度均高于VIP1-GA-BP和VIP2-GA-BP。

表3 两靶区SSC反演精度统计
上文已对A组、B组反演参数进行对比分析,且基于A组反演参数的模型反演精度更高,故仅需对各靶区A组、C组反演参数进行对比分析(表4)。两靶区A组、C组反演参数共有43种,盐分指数最多(14种),其次为植被指数(13种),说明盐分指数和植被指数在SSC反演中发挥着重要作用;另外,不同模型筛选的反演参数差异较大,同一模型筛选的反演参数存在区域异质性。玛纳斯靶区A组、C组反演参数数量均为22,共有的反演参数为RVI、S1、Albedo_short、AVI、Elevation、Roughness;三工河靶区A组、C组反演参数数量分别为13、18,共有反演参数为GARI、S2、S3、S6、Elevation、Swir2。两靶区A组、C组共有的反演参数仅为Elevation,说明高程参数不仅适用不同的筛选模型,而且适用不同区域盐渍化土壤研究,原因在于:地表径流为地势较低的土壤表层带来盐分,且地势较低的地方潜水埋深较浅,潜水更易通过蒸发作用使地表积盐[47];同时,高程不易受其他因素影响,且短时间内变化较小。

表4 不同模型反演参数子集
4.2 反演的SSC空间分布及各类盐渍土面积比例
由于本研究仅对土壤进行盐分反演,故对两靶区3组模型反演结果中的水域、建筑用地进行掩膜处理(图10、图11)。可以看出,两靶区3组模型反演的SSC空间分布存在一定差异,且图斑的破碎度较大,而SSC值域范围与实际采样点SSC值域范围的差异均较小。玛纳斯靶区中,GA-BP和VIP2-GA-BP预测的SSC值域范围(分别为0.20~70.00 g/kg、0.18~69.99 g/kg)更接近实际采样点SSC值域范围(0.18~70.00 g/kg),三工河靶区中,GA-BP预测的SSC值域范围(2.80~26.39 g/kg)更接近实际采样点SSC值域范围(2.62~26.56 g/kg)。
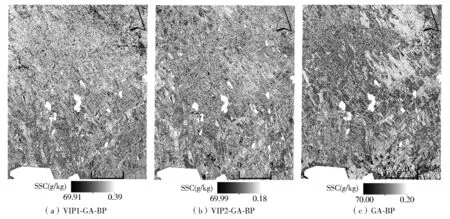
图10 玛纳斯靶区3组模型反演的SSC分布

图11 三工河靶区3组模型反演的SSC分布
土壤属性的空间分布具有空间自相关和空间分异性[48]。为比较3组模型反演SSC的局部特征,在两靶区随机选取3个子区进行对比(图12、图13),发现各子区3组模型反演的SSC空间分布均存在较大差异(可能与模型筛选的反演参数有关),与各模型反演的SSC整体空间分布结果对应;各子区中GA-BP反演的各类地物轮廓最清晰,且地物内SSC的均质性也最好。

图12 玛纳斯靶区子区的位置及SSC分布

图13 三工河靶区子区的位置及SSC分布
由上述分析可知,GA-BP反演精度最高,故参照新疆盐碱土分类标准[27],基于GA-BP反演的 SSC将两靶区土壤划分为5类(图14,彩图见附录3),并统计各类盐渍土的面积比例(图15)。在玛纳斯靶区,盐渍土面积占比最高(55.87%),其次为非盐渍土(16.60%),二者多呈块状分布,重度盐渍土、中度盐渍土、轻度盐渍土多呈点状分布。在三工河靶区,中度盐渍土面积占比最高(51.02%),其次为轻度盐渍土(16.60%),盐渍土面积占比最小(1.54%),各类盐渍土多呈块状分布,盐渍土、重度盐渍土主要分布在靶区北部。从盐渍土分类结果及各类盐渍土面积占比看,玛纳斯靶区土壤盐渍化程度较三工河靶区严重,这与两靶区采样点SSC的统计结果吻合。
5 结论与讨论
在新疆玛纳斯流域和三工河流域各选一靶区,基于Landsat-8 OLI、Sentinel-1 SAR影像数据和SRTM高程数据构建反演参数,通过VIP、GA、BPNN建立3组优化模型,进行SSC反演并统计各类盐渍土的面积比例。结论如下:1)模型反演精度由高到低排序为GA-BP、VIP1-GA-BP、VIP2-GA-BP,表明同步优化反演参数和模型参数的特征筛选方式效果最好,这与Xu等[11]的研究结果相似。2)盐分指数和植被指数在土壤盐渍化反演中起着重要作用,同一模型筛选的反演参数存在区域异质性,但高程适用不同的筛选模型,具有较强的鲁棒性,与王飞等[5]的研究结果对应。3)两靶区3组模型反演的SSC整体空间分布图图斑破碎度均较大,SSC值域范围与实际采样点SSC值域范围的差异均较小;各子区中3组模型反演的SSC空间分布均存在较大差异,其中GA-BP反演的SSC空间分布地物轮廓最清晰,且地物内SSC的均质性最好,这与朱阿兴等[48]的土壤数字制图理论相符。4)玛纳斯靶区土壤盐渍化程度较三工河靶区严重,两靶区面积占比最大的盐渍土类型分别为盐渍土和中度盐渍土。
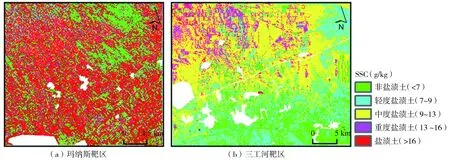
图14 两靶区各类盐渍土的空间分布

图15 两靶区各类盐渍土的面积比例
本研究利用GA-BP进行SSC反演,取得了不错效果,但GA优化的反演参数子集和模型参数可能是局部最优,今后可借鉴统计学中置信度检验的思想,设定衡量优化的参数为全局最优可信度指标[49,50];研究中将一些反演参数设为经验值,算法GA、BPNN也有部分参数是人为设定的,加之本研究没有两靶区实际的土壤盐分含量分布图,只能通过测试集数据判断结果优劣,具有一定的不确定性;运用GEE云计算功能提取反演参数集时,仅考虑VV极化方式的微波物理量,后期可以综合考虑多种极化方式的微波物理量,采用Python或JavaScript语言,并移植到GEE云计算平台中,进行大范围智能化的土壤盐渍化反演研究。
