K-means结合RBF神经网络预测线性菲涅尔集热回路出口熔盐温度

张志勇，路小娟，孔令刚，范多进，姚小明

（1. 兰州交通大学光热储能综合能源系统工程研究中心，兰州 730070； 2. 兰州交通大学光电技术与智能控制教育部重点实验室，兰州 730070；3. 兰州交通大学自动化与电气工程学院，兰州 730070）

0 引 言

能源问题已成为全球的焦点，可再生能源和清洁能源的开发已成为大趋势[1]。太阳能作为最丰富的可再生能源，受到世界各国的广泛关注，太阳能光热发电首先将太阳能转化为热能，大规模的储热手段使得太阳能光热发电可作为基础能源或者调峰电源[2-4]。根据聚光形式，太阳能聚光系统主要有槽式、线性菲涅尔式、塔式和碟式等，在众多的光热电站中，线性菲涅尔式聚光器具有结构简单，风阻小、成本低、土地容积率高及聚光均匀等特点，正逐渐成为最具竞争力的光热发电形式[5-6]。

太阳能光热应用中，过热蒸汽温度提高可以有效提高汽轮机的发电效率。熔盐具有热稳定性好、定压比热容高、工作温度范围广及环境友好等特点，在光热应用中得到了广泛的应用。以熔盐作为传热及储热介质，熔盐工作温度一般设计为550 ℃，蒸汽参数可达538 ℃，相对于其他传热介质，可极大的提高汽轮机的发电效率，同时，单一的传储热介质有效简化了系统的运行工艺[7]。线性菲涅尔集热回路出口熔盐温度的稳定控制对于菲涅尔光热电站高效运行具有重要的意义，出口温度的稳定运行可以保证高品质蒸汽参数的获得，同时，稳定的出口温度可以使传输管路、集热系统、熔盐储罐等设备受到的冷热冲击尽量减少，增加设备的使用寿命。影响集热回路出口温度的因素中辐照强度、入口流量、环境温度、风速、集热器效率等都是时变的，对于线聚焦方式的熔盐菲涅尔式聚光集热系统，太阳能电站的工作温度设计为550 ℃，为满足熔盐的高温需求，集热回路需要有足够长度，以敦煌示范电站集热回路为研究对象，集热回路长度1 100 m，出口温度影响因素的随机性和不可控性[8]导致线性菲涅尔式集热回路出口温度存在较大非线性和滞后特性，难以获得准确的数学模型[9-10]。通过假定一些条件建立数学模型，可以对集热回路出口的温度进行预测，但是假定条件的理想化使得模型的输出结果与实际值存在较大偏差，实现集热回路出口熔盐温度的准确预测可有效提高系统运行的稳定性和安全性，同时，精确的温度预测可以为入口流量的调控做出相应的指导，对电站的运行和系统的安全具有非常重要的意义。

严倩雯等[11]将传统理论模型与BP（Back Propagation）神经网络相互耦合，建立槽式系统工质出口温度的神经网络预测模型，预测模型的相对误差保持在3.6%以内Leon 等[12]利用简化的数学模型对太阳能集热器的传热性能进行分析；Zima 等[13]基于能量守恒方程建立集热管一维数学模型，研究集热管的瞬态传热过程；Khelifa等[14]和Kalogirou[15]采用不同的假设建立槽式集热器的热性能模型；Yan等[16]基于BP神经网络对太阳能集热器气体温度进行预测。在上述研究中，采用传统数学模型方法时需要做出大量假设，导致仿真精度不高且运算复杂，通过建立系统局部模型研究集热管的瞬态传热过程，工程应用存在局限性，将传统模型与BP神经网络结合，对槽式、碟式系统系统出口温度进行了预测的方法因结构差异不能很好的适用于线性菲涅尔太阳能系统。目前RBF（Radial Basis Function）神经网络模型应用于熔盐线性菲涅尔集热回路出口温度预测的研究甚少，因此，采用RBF神经网络模型进一步对熔盐线性菲涅尔系统传热特性进行探索研究具有非常重要的实际应用价值。

针对线性菲涅尔集热回路热性能研究中数据信息波动大、非线性、大滞后的特点，并考虑到准确的传热数学模型获取困难，本文基于径向基函数（RBF）神经网络建立集热回路出口熔盐温度预测模型，通过大量实测数据动态训练神经网络，引入自适应聚类分析的方法预先处理训练样本，降低网络的复杂度和训练速度，采用梯度下降法动态调整、确定隐含层基函数中心和扩展常数，基函数输出的网络权值采用伪逆矩阵的方式确定。将训练好的预测模型应用于敦煌50 MW熔盐线性菲涅尔光热示范电站，对集热回路出口熔盐温度进行实时预测，验证预测模型的实用性，以期对线性菲涅尔式聚光集热回路出口熔盐温度进行有效预测，为线性菲涅尔式太阳能光热电站的商业化运行提供可靠的技术支持。

1 线性菲涅尔集热系统分析

1.1 线性菲涅尔集热系统组成

线性菲涅尔聚光集热系统主要由一次反射镜、二次聚光器（Compound Parabolic Concentrator，CPC）、真空集热管和跟踪控制系统组成，二次聚光器和真空集热管构成吸热系统。在跟踪控制系统的驱动下，一次反射镜实时跟踪太阳，将阳光反射至CPC，经CPC二次反射后投射到真空集热管上，加热管内流动的介质，从而将太阳能转化为热能进行储存。线性菲涅尔集热系统结构图如图1所示，聚光集热系统测试回路实际照片如图2所示。

1.2 集热回路传热模型

敦煌50MW熔盐线性菲涅尔光热电站由80个集热回路构成，集热回路长度1 100m，集热回路入口、出口各设置两个测温点，回路中间设置若干温度测点，在CPC和真空集热管组成的吸热系统中，CPC将太阳光反射至集热管，太阳光透过集热管玻璃外管后被内部不锈钢管壁外层的高温选择性吸收膜吸收，然后将能量传递给管内的熔盐介质。线性菲涅尔聚光集热系统结构图如图3所示。根据导热、对流、辐射传热定律，真空集热管玻璃外管、玻璃内管、不锈钢西热管、管内熔盐介质的能量守恒方程如式（1）～式（4）所示。

式中Tge为真空集热管玻璃管外壁温度，℃，Ta为环境温度，℃，Tgi为真空集热管玻璃管内壁温度，℃，Tr为真空集热管内部金属管温度，℃，Tf为金属管内流体的温度，℃，Tin为集热回路入口介质温度，℃，R1、R2、R3、R4、R5分别为不同部件之间的传热热阻，K/W，Qsb为真空集热管金属内管吸收的能量，J，C为熔盐的比热，J/(kg·℃)，Msalt为熔盐质量，kg，V为熔盐介质体积，m3，ΔT为温差，℃，ρ为熔盐的密度，kg/m3。

真空集热管内管吸收的能量、熔盐介质吸收的能量和系统的总热损如式（5）、（6）、（7）所示。

式中I为太阳直射辐照，W/m2，S为集热支路聚光镜面积，m2，η为集热系统的综合效率，%。

真空集热管金属管与玻璃管之间的真空夹层可以有效降低传热损失。真空集热管金属管与玻璃管内壁之间的传热主要为辐射传热，玻璃管内壁与外壁之间传热主要为导热传热，玻璃外管与空气之间传热主要为对流传热，金属内管与熔盐介质之间传热主要为对流传热，对于整个集热回路，真空集热管之间的接头通常为裸管加保温层结构，接头处同时存在对流、导热及辐射传热。根据传热学的基本原理及式（1）～（6）的传热模型，对于玻璃管管壁与空气的对流传热，环境温度、湿度及风速对传热具有明显的影响，对于金属内管与熔盐介质的对流传热，熔盐介质温度、流量对其传热具有明显的影响。集热系统热传导过程中的所有能量均来自于太阳辐照，集热系统所吸收的能量主要由太阳辐照和集热系统的效率决定，辐照强度越好，聚光集热器效率越高，热损越小，集热回路出口温度就会越高。因此，通过上述传热学的原理分析可知，影响集热回路出口温度的因素主要有太阳直射辐射、集热系统效率、风速、环境温度、大气湿度、熔盐入口温度及熔盐流量。

2 集热回路出口盐温预测控制策略

集热回路出口温度的影响因素众多，且具有非线性、时变等特点，同时，熔盐线性菲涅尔示范项目中集热回路长度为1 100 m，出口温度的响应具有很大的滞后性。熔盐介质流经集热管集热的过程中逐段被加热，集热回路中不同加热段的熔盐进、出口温度不同，加热过程中随着熔盐温度的提升，介质与环境温度温差的增大使得集热回路的热损逐渐增大，各种时变参数导致使用传统数学预测模型控制时存在计算过程复杂、计算量大、预测结果误差大等缺点。

RBF（径向基函数）是一种将输入矢量扩展到高维空间中的神经网络学习方法[17-19]。采用RBF神经网络进行集热回路出口熔盐温度预测，可以理解为根据当前采集的实时参数信息，将该组参数信息划分到根据训练样本训练后的不同分组中，根据该分组中输入、输出信息的非线性关系实现集热回路出口熔盐温度的实时预测，RBF神经网络能够以任意精度逼近任意连续函数，特别适合解决分类问题。

根据线性菲涅尔集热回路的热学特性，选择以太阳辐照度I、集热系统综合光热效率η、风速W、环境温度Ta、大气湿度Hu、集热回路入口温度Tin、集热回路入口流量Qin作为网络输入参数，以神经网络预测的集热回路出口熔盐温度Tout为输出参数。因此，设定神经网络输入层节点为7，输出层节点数为1，输入输出关系如式（8）所示。

2.1 预测控制网络模型

用径向基函数作为隐含层神经元的基构成隐含层空间，这样就可以将输入矢量直接映射到隐层空间。当基函数中心确定后，这种映射关系也就确定了，而隐含层空间到输出层空间的映射是线性的，即输出是隐层神经元输出的线性加权和[20-21]。构造和训练一个RBF神经网络就是要让映射函数经过学习，从而确定每个基函数的中心Ci，宽度δi和权值ωM，最后完成输入到输出的映射[22-26]。基函数以输入空间的点x与中心xM的距离作为函数的自变量，各基函数的形式如式9所示。

式中φ为基函数，为空间点x与xM的距离，M为隐含层节点数，即基函数的数量。

基于径向基函数的输出定义为基函数的线性组合，表达式如式（10）所示。

式中F(x)为网络输出值，ωM为第M个基函数对应的权值。

设训练样本的个数为P，隐含层节点数为M。众多训练样本的输出构成线性方程组如式11所示。

若Φ为可逆矩阵，通过（13）式可求解出系数向量ω。即

2.2 基于K-means方法的RBF神经网络

隐层神经元参数（中心，宽度）的确定一般要采用非线性优化的策略，RBF网络实现从输入空间到隐含层空间的非线性变换依赖于RBF中心的数目，位置以及作用域宽度[27]。对于线性菲涅尔集热回路出口熔盐温度的预测，本文基于改进的K-means方法构建RBF网络模型，样本点选用集热回路集热运行过程中，直射辐射、集热效率、风速、环境温度、湿度、集热回路入口熔盐温度、集热回路熔盐流量及集热回路出口熔盐温度间隔1min的历史数据，首先在样本点中随机选取M个点作为初始聚类中心，对样本进行均值聚类，之后通过梯度下降法确定各聚类中心，聚类中心确定后，根据各中心之间的距离确定对应径向基函数的扩展常数，这种自适应聚类学习算法，隐含层基函数的中心和扩展常数在训练过程中自动调整确定，算法结束即为最优。实际网络训练中，输入样本数远远大于径向基函数的中心数目，各隐含层的输出权值采用式（14）的变形结构式（15）计算。

式中ω为权值系数向量，Φ为基函数矩阵，ΦT为基函数的转置矩阵，Φ-1为基函数的可逆矩阵，d为输出向量。

网络训练的具体过程如下：

1）确定RBF网络的中心，根据训练数据的维数，确定隐含层中心的数量为M，首先在样本数据中随机选取M个数据中心Ci,i=1,2,…,M，从第一个样本数据X1开始，计算X1与每个基函数中心的距离||X1-Ci||，i=1,2,…,M,找出距离最近的中心，将样本点聚类到该中心，通过上述方法将P个数据样本逐个进行聚类，每个聚类中样本点存放在矩阵A中，各聚类中的样本数量计为B，数据中心存放在矩阵C中。

2）将每个聚类里的样本点按列相加，之后确定每个聚类新的中心为C_new=sum(A)/B。

3）求出每个基函数中心与新中心距离，即中心差值向量的2范数。

4）循环学习优化，直至基函数的中心与新中心的距离小于0.1时，跳出循环，经过学习优化的中心即为最终基函数的中心，中心向量存储在矩阵C中。

我也交到了一个外国朋友，他是一个意大利人，我们被分在一个班，经常坐在一起讨论问题。虽然语言有些不通，但我们俩配合得非常默契。离别时，我们都非常不舍，还留下了对方的联系方式。

5）确定扩展常数δ，从第一个中心开始，将中心矩阵的每列与第一个中心向量做差值，即||C-C(:,i)||，i=1,2,…,M，扩展常数δ=min(||C-C(:,i)||)，δ≠0，依次得出各径向基函数的扩展常数δ。

6）确定权值矩阵，根据式（15）通过求解伪逆矩阵的方法求解网络的权值矩阵。

根据上述网络训练过程，通过MATLAB编程可以很容易的实现预测网络的参数训练及输出预测，预测网路的实时性和运算效率相比传统传热数学模型预测具有极大的提升。

3 非线性预测网络训练

3.1 输入样本

网络训练样本的选择需要满足3个条件：遍历性、致密性、相容性[28]。遍历性要求选择的样本覆盖到所有的样本区域，不能集中在一个区域，否则会影响网络的泛化能力；致密性要求样本的数量尽量多，样本数量越多，训练样本的致密性越好；相容性即需要剔除输入相近而输出差异很大的样本。

文中以敦煌大成50MW熔盐线性菲涅尔光热示范电站2020年6月22 min-1实测数据为训练样本，训练样本选择尽量满足遍历性、致密性和相容性，原始数据呈现曲线如图4所示。图4a为集热回路入口流量变化曲线，图4b为太阳直射辐照强度变化曲线，图4c为集热回路入口温度变化曲线，图4d为环境温度变化曲线，图4e为环境湿度变化曲线，图4f为风速变化。

线性菲涅尔聚光集热系统综合光学效率随季节和早中晚的时间逐渐变化，夏季与冬季因太阳高度角的差异，余弦效率、末端损失效率等具有很大差异，导致集热系统综合光学效率相差较大；早中晚时刻，镜列的遮挡与阴影导致集热系统的综合光学效率存在较大差异，线性菲涅尔系统2020年全年典型日光学效率曲线如图5所示。从影响集热回路出口熔盐温度的输入参数的波动曲线可以看出，集热回路正常运行过程中，集热回路入口流量、太阳直射辐射强度和环境风速会出现剧烈波动情况，集热回路入口温度，环境温度，大气湿度等不会出现剧烈波动情况，集热系统的综合光学效率在早晨及傍晚时变化比较明显，在正午前后最佳集热过程中集热效率不会出现剧烈波动情况。

3.2 数据处理

在线性菲涅尔集热系统的输入参数中，太阳辐照、入口流量的波动对出口熔盐温度的影响最为明显。夏季时，大气对流现象较为频繁，大气对流极易生成云团，冬季时，大气对流现象减少，天空云团较少，天空云团对太阳的遮挡造成直射辐射参数的波动，辐照强度的变化作用范围是整个集热回路，流量的的波动作用范围是集热回路入口。线性菲涅尔集热系统属于线聚焦集热类型，集热回路对介质的传热是一个累积的过程，集热回路长度1 100 m，熔盐介质的设计流速为0.5～2 m/s，夏季时流速一般为1～2 m/s，冬季时流速一般为0.5～1 m/s，辐照波动夏季较为频繁，按照夏季熔盐流速为1.5 m/s考虑，熔盐从集热回路入口到出口需要大约12 min，在选择训练参数时，根据熔盐流速和辐照等参数对出口熔盐温度影响的滞后性，将训练样本的输出值在时间上推迟平移12 min，使网络预测结果更接近系统实际输出。

利用RBF神经网络对集热回路出口熔盐温度进行预测，由于各项数据之间存在不同量纲，导致数据之间存在较大的差异，因此，为了取得理想的预测效果，在将数据输入训练网络前，需对数据进行归一化处理，利用MATLAB软件中premnmx(X)将数据统一到[-1,1]之间。处理后的输入数据趋势如图6所示。

3.3 网络训练

根据实测数据，尽量选择辐照强度覆盖全有效辐照范围内的数据，设定不同的隐含层节点数，根据不同隐含层网络节点数的模型采用相同的样本数据训练网络，训练好网络参数后，将训练的样本数据输入网络，通过网络预测出样本输入数据的预测输出温度，根据网络参数性能评价标准，分析比较，选择理想的隐含层网络节点数，确定出RBF网络模型。

对于网络模型的评价，本文采用常用的最大绝对误差（MRERR）和最大平均绝对百分误差（MAPE）作为预测模型的评价指标[29-30]，具体公式如下：

最大绝对误差（MRERR）：

平均绝对百分误差（MPAE）：

式中Yi为实测值，为预测值，P为样本点数。

预测结果的最大绝对误差（MRERR）和平均绝对百分误差（MAPE）的值越小表示误差越小，预测的准确度越高。本文取敦煌光热电站2020年6月22日的实测数据作为训练数据，训练样本点577个，不同隐含层节点数M对应的神经网络预测输出如图7所示，网络性能参数评价如表1所示。

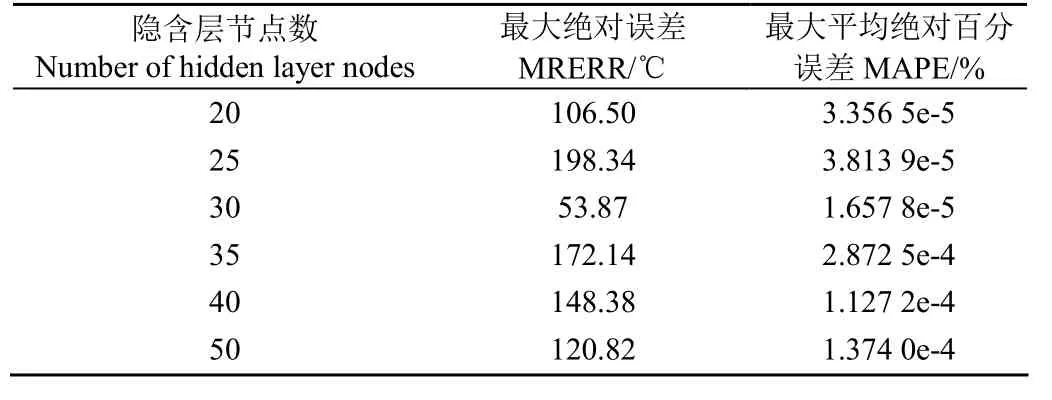
表1 不同隐含层节点数RBF网络性能参数对比Table 1 Comparison of RBF network performance parameters of different hidden layer nodes

从表1可以看出，不同的隐含层节点数所训练出的网络性能参数具有一定的差异，当隐含层节点数选择30时，即基函数的个数为30时，可获得相对最小的平均绝对百分误差MAPE和相对较小的最大绝对误差MRERR。通过图7预测结果与实测值的图形对比，综合MAPE及MRERR的值，确定RBF神经网络模型隐含层节点数取值为M=30。

3.4 模型验证

根据3.3节确定的RBF神经网络基函数中心C和扩展常数δ，选择2020年6月15日、6月16日、6月18日及7月5日的实测数据对建立的网络预测模型进行验证，隐含层输出的权值矩阵根据实际输入数据实时计算，RBF神经网络预测输出结果如图8所示，图8中每张子图下方为集热回路入口流量变化曲线。

图8a中，13：10左右，辐照急剧下降，流量未及时跟随辐照下降而调低时，集热回路出口温度迅速下降；15：40到15：47，云团完全遮挡太阳，为维持集热回路出口温度稳定，及时调低流量，但云团对太阳的长时间遮挡导致集热回路出口熔盐温度持续降低。从预测输出的结果可以看出，在13：00、15：50及17：50几个时间段内，当辐照、流量出现频繁波动时，预测输出结果依旧能很好的跟随实际输出结果。

图8b中，9：50前后的时间段，11：00前后的时间段，辐照和流量均出现一定的波动。12：45左右，辐照相对稳定，但流量波动较为频繁。从总体的预测输出结果可以看出，全天辐照波动相对较小，当流量频繁波动时，预测输出结果与实测值出现相对较大的预测误差，流量参数的突变导致预测输出结果在该点附近的误差最大，但集热器出口温度总体趋势较为平稳。

图8c中，全天时段内辐照波动频繁、剧烈，同时辐照强低，为获得较高的出口温度，集热回路流量控制的较小，且流量调整不频繁，集热回路出口温度跟随辐照变化趋势上下波动。从预测输出的结果可以看出，在辐照频繁、剧烈扰动的情况下，预测输出结果同样能够很好的跟随实际输出值。

图8d中，辐照参数在10：45之前较为稳定，9：45时，集热回路出口温度超过400 ℃，此时调低集热回路流量快速升温；11：17左右，集热回路出口盐温接近550 ℃上限值，增大流量快速降温，防止系统超温；从预测输出结果可以看出，9：45时，流量的剧烈波动导致该时刻点附近预测输出出现较大偏差11：20到12：00时间段内流量的频繁调整导致预测输出结果与实际输出值存在相对较大偏差。

从图中8d的预测结果和实际输出值对比中可以看出，在流量或者辐照剧烈波动的情况下，预测结果与实际输出值会出现较大的偏差，但预测输出的总体趋势与实际输出值大致接近，通过对实测数据进行仿真可以得出：在输入参数实时波动的情况下，基于K-means方法的RBF神经网络预测模型能够很好的实现线性菲涅尔集热回路出口温度的预测输出，通过8d的实测数据对网络进行验证，最大绝对误差（MRERR）为121.23 ℃，最大平均绝对百分误差（MAPE）为3.576 2×10-4%。最大绝对误差反应预测网路的局部预测效果，在流量、辐照剧烈波动的情况下，预测输出的误差会有较大的偏差，最大平均绝对百分误差衡量的是预测准确性的统计指标，即预测网路的总体趋势，从最大平均绝对百分误差的数值看，该预测网络具有较好的预测性能。

4 结 论

通过敦煌光热示范电站线性菲涅尔1 100 m集热回路实测数据训练网络，对比不同隐含层节点数下RBF神经网络温度预测输出结果可以得出：

1）隐含层节点数较少时，网络的逼近能力和泛化能力降低，隐含层节点过多，网络会出现过拟合现象。

2）对于线性菲涅尔集热回路出口温度预测模型，根据输入参数的特点，隐含层数量M选择为30时，预测网络可得到较为理想的输出结果。

3）基于该温度预测模型，通过6月15、6月16、6月18和7月5日4d的预测输出与实测值对比结果得出，网络输出的最大平均绝对百分误差为3.576 2×10-4%，最大绝对误差为121.23 ℃。从预测网络对出口温度的预测效果来看，该网络能够很好的对集热回路出口温度进行预测，该RBF神经网络能够较为理想的实现大滞后、多扰动系统的预测输出，对线聚焦光热电站熔盐温度的稳定调节具有一定的应用价值。

敦煌光热示范电站线性菲涅尔集热回路长度1 100 m，熔盐从集热回路入口到出口，输入端参数波动经过较大的滞后才能在出口体现，实际运行中，直射辐射的变动最为频繁，辐照的变化引起入口流量等的调整，根据太阳能光热系统的运行特点，实际运行中集热回路入口熔盐流量的调整不能太过频繁，因此，样本数据中因为人为干预及部分时变因素的扰动使得训练样本很难满足各种输入参数的工况条件，所以样本的遍历性有一定的局限性，从上节预测结果可以看出，网络预测输出值的最大平均绝对百分误差较为理想，但最大绝对误差仍然较大，后续的研究中还需对输入样本的选择进行优化，使网络参数更加理想，减小预测输出的最大绝对误差。