排水泵站整流底坎参数优化

李志祥，冯建刚，钱尚拓，徐 辉,

（1. 河海大学水利水电学院，南京 210098；2. 河海大学农业科学与工程学院，南京 210098；3. 西藏农牧学院水利土木工程学院，林芝 860000）

0 引 言

排水泵站易受地形地质条件限制和周围建筑约束，进水建筑物布局紧促，难以达到泵站设计规范要求的占地面积和布置形式。紧凑的布置方式使得泵站进水建筑物内常常存在回流、漩涡、偏流等不良流态，进而影响水泵进流条件，引起水泵性能下降，造成汽蚀、机组振动等问题，严重影响泵站的安全稳定运行[1]。为此，在排水泵站前池设置整流措施，改善进水建筑物内的不良流态，对保障泵站安全运行具有重要意义。

底坎作为广泛应用的整流措施，能够有效改善前池流态，通过挑流及坎后的漩滚作用，破坏前池两侧回流形成条件，促进水流充分紊动扩散，从而在进水池入口处获得满意的流速分布[2]。该措施施工简单、经济易行、效果显著。曾昊等[3]在泵闸工程应用一字型底坎，讨论一字型底坎对出流流态的影响，分析其参数变化的影响效果；罗灿等[4]采用计算流体力学（Computational Fluid Dynamics，CFD）数值模拟技术研究前池底坎整流措施，探讨了底坎位置、高度及顶宽对整流效果的影响，提出前池底坎设置方案；冯建刚等[5]针对泵站前池的布置特点，提出了导流墩结合底坎的组合式整流措施，对正向、侧向进水泵站前池流态均有较好的改善效果。目前，研究者对前池底坎整流措施水力优化设计研究较少，且通常采用控制变量法比较设计参数对流场水力特性的变化，略去底坎设计参数同时变化对三维流场水力特性的耦合作用。

响应曲面模型能通过试验获得响应变量与设计变量之间的多项式函数关系，从而提高优化效率[6]。即通过拟合目标变量与设计变量之间各种阶数的模型，描述二者之间存在的未知、复杂函数关系，由此作为二者之间真实函数关系的一种近似，并对其进行模型分析[7-9]。资丹等[10]将其应用于泵站进水池垂直吸水管布置优化分析中，给出淹没深度、最优悬空高、后壁距的最优组合；高学平等[11]应用响应曲面法建立以抽水蓄能电站进/出流时的流量分配等多个水力指标作为目标函数，拟合了以扩散段长度等作为设计参数的响应模型。因此，可以考虑将响应曲面优化设计方法应用到前池整流措施参数优化分析中，利用其可以给出设计变量与目标值之间函数关系的优势，找出最优设计，降低数值计算工作量，提高计算效率。

针对底坎整流措施体型及布置参数多目标优化问题，本文拟考虑坎高、坎距的耦合影响，提出结合信息量权数法的响应曲面模型，并对整流底坎的高度和布置位置进行参数优化。建立表示流场水力特性的综合目标函数与整流底坎设计参数的多项式函数关系式，得出最优底坎体型及布置参数，改善泵站进水建筑物内流场流态，以期为同类泵站的整流措施设计和优化提供参考。

1 排水泵站数值模型与验证

1.1 排水泵站计算模型建立

图1是典型的排水泵站结构图[12-13]，泵站结构设计参考上海新宛平泵站及文献[12]中的泵站布置形式，其典型特征表现为水流正向进流，前池扩散角大，水泵机组对称布置。泵站进水建筑物总长4.1 m，包括引渠段、扩散段、前池、进水池、喇叭口和吸水管。引渠段长度为2.0 m，前池扩散角为44°，吸水管喇叭口直径为97.5 mm，单个机组进水池宽度D为270 mm。前池水位H为300 mm，单泵排流量为5 L/s。

1.2 排水泵站水力性能的数值模拟方法

基于雷诺时均纳维-斯托克斯方程（Navier-Stokes equations，N-S方程）和剪切应力传输模型（Shear Stress Transfer，SST），对泵站进水建筑物内水流流动情况进行模拟。SSTk-ω模型能预测泵站内部在逆压梯度作用下出现的水流分离流动现象及回流区范围[14]。控制方程基于有限体积法进行离散，计算时离散格式对流项采用二阶迎风格式，扩散项和源项采用中心差分离散格式，数值求解方法采用半隐式方法SIMPLEC算法[15-16]。自由液面采用刚盖假定法，数值计算的定解条件如下：泵站引渠进口设置为正交速度进口，计算域出口设置在吸水管末端，采用自由出流的方式，进水建筑物内自由液面处设为刚盖假定法的对称边界，其他固体边界设置为标准式壁面函数下的无滑移壁面边界。为保证网格质量，采用ICEM CFD（The Integrated Computer Engineering and Manufacturing code for Computational Fluid Dynamics）对泵站进水建筑物进行六面体结构化网格划分，对比5套粗细不同网格方案（网格总量为62～285万），综合考虑计算效率和精度，最终选取网格数量为1 363 996[17]。图2为泵站数值模拟的计算模型示意图。

1.3 排水泵站计算模型验证方法与结果

1.3.1 排水泵站物理模型试验方法

针对泵站进水建筑物无整流措施计算结果，通过对比数值模拟和物理模型试验的表面流线及流速分布结果，分析本文构建的泵站数值模型及模拟方法的可靠性。

图3是泵站试验模型照片，物理试验模型按照图1泵站结构图1:1建立，采用全透明泵站进水建筑物自循环开敞式系统，包括引渠段、前池、进水池、吸水管、出水池、管道离心泵、回水管、进水箱、整流栅等。图1所示的流速测点由光电流速仪进行量测，光电流速仪的精度为1.0%。泵排流量由安装于水泵出水管上的转子流量计进行量测，精度为±2%。试验中，前池进水池水位由水位测针量测，水位测针采用南京水科院制作的高精度复式测针，测针读数误差为±0.1 mm。

1.3.2 结果与分析

图4是数值模拟和物理试验获得的表层流线图。从试验流线可知，前池两侧存在大范围回流区，其回流范围从扩散段中部延伸至进水池入口，回流中心点位于扩散段末端附近，与外侧边壁的垂直距离约为0.8D。此外，边缘进水池隔墩背水侧也存在着较大范围的漩涡，漩涡分布在隔墩头部和吸水管间。数值模拟所得的流线图反映的前池两侧回流范围、回流中心、形态及进水池隔墩背水侧漩涡与试验现场观测的流态吻合度很高，表明数值模拟能很好预测到前池、进水池内存在的回流、漩涡等不良流态。

图5为扩散段末端面层的流速分布图。为了方便比对，将扩散段末端位置各点x方向流速u与引渠段进口平均流速um相除，实现流速无量纲化，并作为纵坐标；横坐标为y/D，D是进水池宽度，中间位置y/D=0，左侧边壁横坐标为-2.28。由图可知，u/um在y/D=0附近有较大值，数值模拟与试验测得的较大流速均出现在前池中部。数值模拟结果能够预测到水流受到逆压梯度力的影响在前池两侧形成较大范围的回流区，总体流速分布规律与试验值所示基本一致。扩散段末端面层流速分布模拟值和试验值的R2为0.98，均方根误差（Root Mean Square Error，RMSE）为0.06，进一步表明本文泵站数值模型及其水力特性数值模拟方法的可靠性，可以用于后续的整流底坎参数优化计算。

2 基于数值模拟方法的泵站整流底坎参数优化

2.1 泵站底坎整流参数设计

底坎整流作为流体分离流动理论在水利工程上的应用，泵站进水建筑物内流场流态复杂，存在高曲率大变形的流动，在既定泵站设计尺寸和运行条件情况下，底坎的整流效果主要受坎高、坎厚和底坎的位置影响[18]。而前人的研究成果表明[2-4,18]，当整流底坎厚度在坎高某倍数范围变化不会对流态产生显著影响。所以，本次数值方案仅考虑泵站固定流量下，底坎的坎高和布置位置对泵站进水建筑物水头损失、涡量、流速分布的影响。

为详细研究坎高、布置位置取值对目标函数的影响，依据前置试验[19]，对两者最优范围进行适当的缩小，坎高、布置位置的取值范围：坎高h取0.1H～0.34H，底坎布置位置d取4.5D～6.5D。这里底坎布置位置即坎距，指底坎迎水面到吸水管中心线的水平距离，如图1和图2所示。样本空间采用析因设计获得，相比其他试验设计方法，析因设计在参数取值范围内采样更加均匀且获得信息量巨大，能准确估计出坎高、布置位置的主效应及交互影响。如果采用Design-Expert自带的外切中心复核设计等试验设计方法，系统会根据研究因素数目（本文为2），自动给出13组样本，其中有4组样本为重复样本，此时，因为计算样本较少而难以建立精度较高的响应曲面模型。更多水平数的设计会使得优化工作量呈现指数式增长，而计算精度得不到显著地提升。综合考虑优化计算的成本及效率，在坎高、坎距的取值范围均匀选取5个点，进行二因素五水平自由组合，得到25个样本空间，如表1所示。采用本文构建的数值模型和数值模拟方法对该设计样本，进行CFD数值计算，得出整个泵站进水系统计算域的水力损失系数、控制断面的流速不均匀系数和喇叭口涡量特征值。

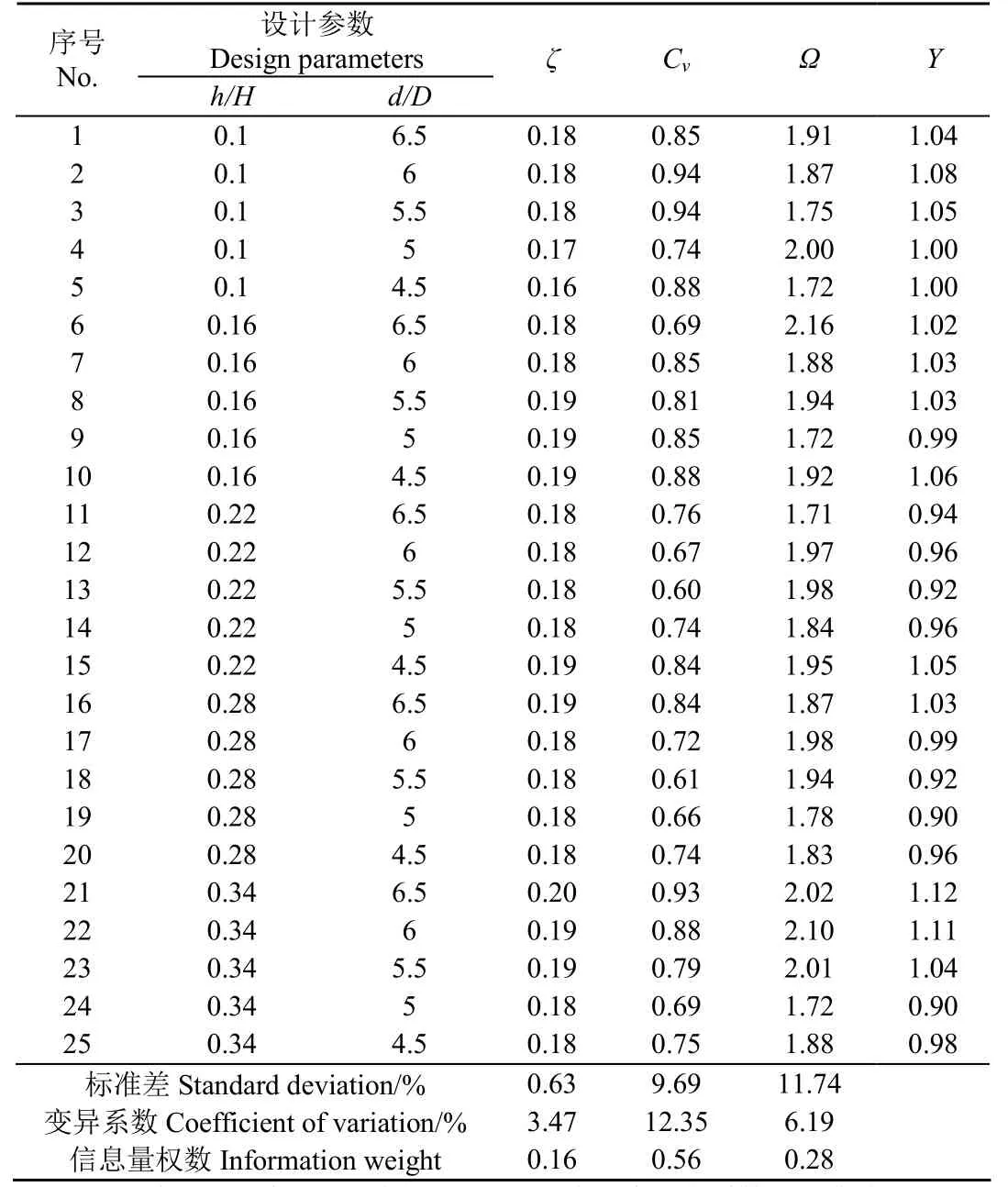
表1 泵站底坎整流参数设计及整流效果数值模拟结果Table 1 Parameter design of rectification bottom sill in pumping station and numerical simulation results of rectification effect

2.2 水体流态评价指标计算方法

泵站实际运行状态中，进水系统内通常会存在回流、漩涡等不良流态，各个进水池进流不够均匀平顺，会对水泵机组的高效稳定运行造成影响。水力损失、流速均匀度、速度加权平均角度等常作为定量描述泵站进水系统流态的评价指标[10,16]。本文对这3个指标作部分修改。

水力损失系数可以表征泵站运行效率，高效率运行的泵站水力损失较小。采用水力损失系数无量纲数（ζ）定量描述泵站效率，其计算公式如下[11]：

式中hw为水力损失，m；z为计算断面的位置水头，m；为计算断面平均压力，Pa；为计算断面平均速度，m/s；ρ为20℃液态水的密度，kg/m3；g为重力加速度，m/s2；其下标数字1和2分别代表计算域吸水管进口和出口。

流速不均匀系数（Cv）为进水池入口流速标准差与平均流速的比值，常用于评价进水池入口流速分布均匀性的指标。本文采用Cv定量表征泵站进水系统的流场均匀性。优良的泵站进水建筑物水力设计，其前池能够平顺均匀地将水流输送至各个进水池，进水池入口流速大小相近，流速方向均为入口截面法方向，此时流速不均匀系数接近0。Cv计算公式如下[10]：

式中m为进水池进口截面的选取单元个数；ui为各单元i的法向速度，m/s。

漩涡是泵站进水建筑物内流场常见的不良流态，可利用涡量描述漩涡运动。在直角坐标系下，涡量可分为x、y、z3个方向分量，许多学者往往选取某一最能反映该流场特征的漩涡运动分量来分析涡量场特点[10]。使用分涡量就会略去其他方向的涡量值，不能很好反映真实的涡量场信息，为此选用合涡量ω（s-1）表示某处的涡量值大小。环量计算可以描述闭合曲线内的水流旋流程度，而且可以反映该处的漩涡运动强度和漩涡核心大小[20]。本文选取喇叭口截面计算合涡量的平均值，选取其进口圆周线作为积分曲线，计算喇叭口水流预旋及漩涡强度情况。为突出吸水管喇叭口附近涡量特征，将喇叭口合涡量均值与速度环量相乘，采用无量纲形式分析喇叭口附近的漩涡分布特点。本文的评价涡量场优化程度的量化指标可采用式（4）进行计算。

2.3 基于信息量权数法的多目标优化求解方法

底坎的整流效果评价指标有水力损失系数、流速不均匀系数和喇叭口涡量特征值3个目标，对于该类多目标优化求解主要有2种：1）以约束法、权重法或隶属度法将多目标问题转化为单目标进行求解；2）采取多目标进化算法进行求解，生成一系列非劣方案[21]。多目标进化算法往往会伴随着优化对象的大量迭代计算，每次的迭代都需要研究人员重新建模计算，整个优化过程将变得繁杂，耗时过长。所以本文这3个评价指标揉合在一起，赋予不同的权数，凝练为单个综合目标，使得问题变得简单易行[8-10,22]。其中权数的确定是多目标优化方法最为关键的一环，直接影响综合评价的结果，改变目标优劣顺序[23]。信息量权数法[24]是根据评价指标分辨信息多少，将评价目标的这种差异加以量化来确定的权数，可以比较不同评价指标间的优劣，用于处理多目标决策问题。因此，本文采用信息量权数法，将水力损失系数、流速不均匀系数和喇叭口涡量特征值3个评价指标的变异系数归一化处理，确定权数。具体步骤如下：

1）设评价体系里包含K个指标Xk（k=1,2,3,…,K）；每个指标含有n个样本。

2）计算标准差

3）计算各指标的变异系数

4）将Vk归一化处理得到各个指标的信息量权数

5）最终形成综合目标函数形式为

式（5）～式（9）中n为样本个数；为n个样本指标Xk的平均值；Sk、Vk和Wk分别为指标的标准差、变异系数和信息量权数；Y为综合目标函数，由ζ、Cv和Ω三者乘以各自不同的权数形成。理想的整流效果是泵站进水系统水力损失系数极小，水流进流平顺均匀，吸水管喇叭口不存在预旋，进水池不存在附壁涡、附底涡等不良水力现象。Y值越小，泵站前池底坎整流效果越好，泵站运行效率越高。

2.4 灵敏度分析

Sobol’法的中心思想是将函数分解为递增项之和，通过采样计算其总方差和各项偏方差，以求得各参数灵敏度[25]。相比直接求导法等局部灵敏度分析方法，Sobol’法作为全局灵敏度分析方法，不仅可以检验单个参数变化对模型结果的影响，还可考察多个设计参数同时变化对模型的影响。因此，本文基于Sobol’法对建立的响应曲面模型进行全局灵敏度分析，确定设计参数间交互作用。

3 结果与分析

3.1 综合目标函数构建

不同坎高和坎距设计下，整个泵站进水系统计算域的水力损失系数、控制断面的流速不均匀系数和喇叭口涡量特征值如表1所示。h/H为底坎高度与前池水深的比值，d/D为底坎到吸水管中心线的水平距离与泵站进水池单个水泵机组进水池宽度的比值。根据上文信息量权数的求算办法，对表1中数据进行计算，确定变异系数及相应的信息量权数，最终形成加权函数如下：

式中Y为综合目标函数；ζ为水力损失系数；Cv为流速不均匀系数；Ω为喇叭口涡量特征值。

3.2 综合目标函数的响应曲面模型构建

前池底坎的设置改变泵站进水系统的流态，产生的漩滚和挑流作用，使得前池水流紊动剧烈且存在高扭曲大变形的流动，目标函数与影响因素之间的关系因而反映为高度非线性。如果采用一阶或二阶多项式拟合这种非线性关系，则难以反映真实关系，拟合精度难以保证，而更高阶数的多项式虽然在计算域内可能会有更好的拟合效果，但是计算量显著增大，形式复杂，故不采用。本文应用响应曲面模型对表1中的数据进行拟合，建立反映相对坎高、相对坎距与Y之间影响关系的三次多项式数学方程如式（11）所示，为方便起见，采用x1代替h/H，x2代替d/D。

式中x1为相对坎高；x2为相对坎距。

响应曲面模型的误差分析见图6，图中各点分布均贴近1:1线，表明其拟合效果较佳。综合目标函数的R2为0.86，RMSE为0.02，可知响应曲面模型精度较高，拟合的三阶多项式能较好地预测底坎坎高、坎距与目标函数的关系。

3.3 泵站整流底坎参数灵敏度分析

响应曲面模型设计参数的灵敏度分析结果见表2。一阶及总体全局灵敏度系数较大，系数范围为（0.42～0.58），可知建立的响应曲面模型受两个设计参数的变化影响大。其中，相对坎高的一阶全局灵敏度系数大于相对坎距，说明相对坎高对模型影响程度高于相对坎距。一阶全局灵敏度与总体全局灵敏度系数差值大，两设计参数所求得的系数差值均超过其一阶全局灵敏度系数的20%，表明设计参数间存在显著的交互作用。

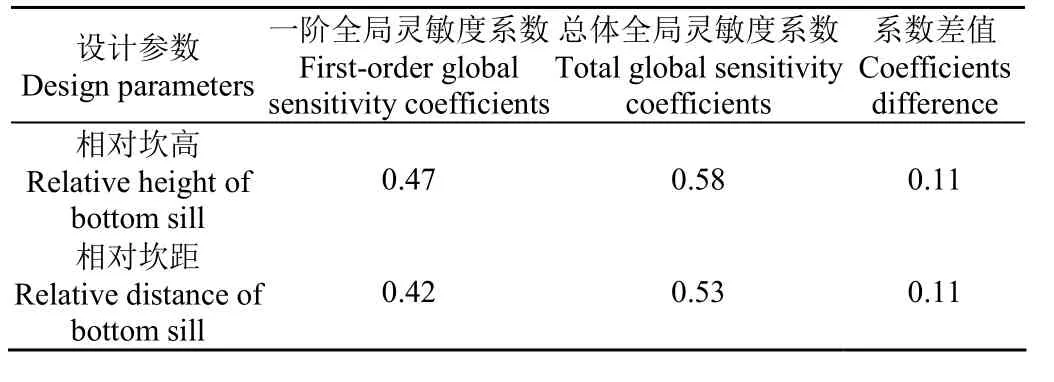
表2 泵站整流底坎参数灵敏度分析Table 2 Sensitivity analysis of design parameters of bottom sill in pumping station

3.4 基于响应曲面模型分析坎高和坎距对综合目标函数的影响

图7为坎高、坎距对目标函数的响应，整流底坎的高度、距离对泵站进水系统三维流场的速度场和涡量场的影响显著。由图7a三维曲面云图可知，总体而言目标函数Y随着相对坎高x1的增大和相对坎距x2的减小，先快速减小后略增大，在研究范围内存在着最小值。x1在0.26～0.32，x2在4.8～5.2之间时，Y有较小值，泵站进水系统流态有明显改善。当x1在0.22以下时，目标函数Y随着x2的变化反应较为平缓，表现为随着x2的增加，先缓慢下降后缓慢增加；当x1在0.22以上时，目标函数Y随着x2的增加先缓慢下降后快速增加。反映为当底坎高度小于0.22H时，流场的流态随坎距的增加先改善后恶化；当底坎高度大于0.22H时，流场的流态随底坎距离的增加先略有改善后急剧恶化。图7b显示相对坎高、相对坎距对目标函数的耦合影响。这2个参数同时变化其耦合效果显著，两者交互影响大。如果坎高和坎距这两个因素之间没有交互影响，则在响应等高线云图上，等高线呈现为一族同心圆。反之，如果响应等高线云图上，等高线发生强烈扭曲，表明二因素交互作用强烈。可见实际上，坎高和坎距同时变化对流场流态的交互影响作用是不可忽视的。

3.5 底坎参数优化

本文以底坎相对高度、相对坎距为优化设计自变量，以综合函数Y作为目标，利用最速下降法求解综合目标函数在计算区域内的最小值。目标函数Y在某点的梯度表示在此处的函数值上升速度最快，则该点的负梯度表明在此处的函数值下降速度最快，最速下降法是使用负梯度搜寻函数在某区域的最小值。通过计算，得出目标函数预测值Y=0.90，此时x1=0.29而x2=5.02。根据上述求解的优化参数，进行CFD数值模拟对比有无整流措施对泵站水力性能的影响，如表3所示，采用底坎整流措施后泵站流速不均匀系数减小19.28%，计算域水力损失系数减小5.26%，喇叭口涡量特征值降低了5.76%，3个定量评价指标均有所减小，说明采用该优化设计方法可大大提高流场内的流态。响应曲面模型与CFD数值模拟所得综合目标函数值的相对误差为1.30%，可认为得到的响应关系式能满足精度要求，能反映底坎高度、坎距对泵站进水系统流场流态的影响。

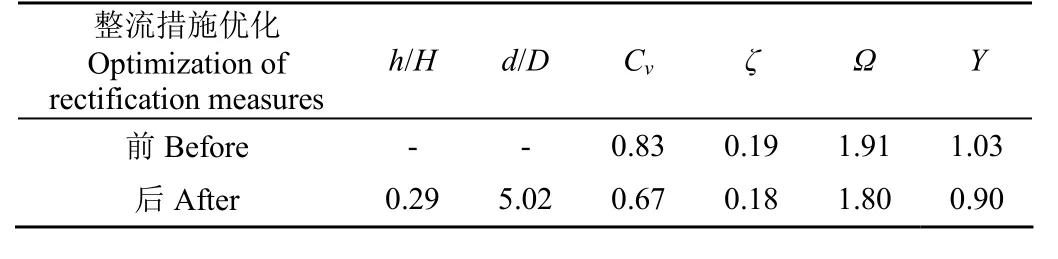
表3 泵站前池整流参数优化前后水力性能对比Table 3 Comparison of hydraulic performance before and after optimization of rectification parameters in the forebay of pumping station

图8为原始方案和优化方案的中层水流x方向流速云图。由图8a可知，水流自引渠流入前池，由于前池扩散角较大，过流面积增大，流速减缓，产生较大的逆压梯度，使得主流与边壁脱流，在扩散段边壁与主流之间形成回流区，回流区甚至延伸至进水池入口。前池回流区的存在会进步压缩主流真实过流面积使得该处的局部流速甚至大于引渠流速，另一方面，主流收到压迫集中直冲中间两个进水池，两侧进水池进水不够顺畅，隔墩处存在明显背水侧漩涡，不利于水泵吸水。从8b图可知，优化后的底坎整流措施，显著改善泵站进水建筑物内的不良流态，前池两侧的大范围回流区显著缩小，隔墩背水侧漩涡完全消失。水体在底坎作用下，相互碰撞、混掺，使得紊动能进一步向前池两侧低动能水体传递，该区域的水体获得相近的流速，促使水流平顺均匀地流向进水池。

图9为机组纵剖面涡量图，这里涡量为合涡量。无论原始方案还是优化方案的最大涡量值出现在喇叭口内侧壁面下方，这是因为进水池内水流从四周绕流进入吸水管，流线弯曲程度大，在流过喇叭口尖端时会产生很强的涡量。对比图9a和图9b，优化后的底坎整流措施，有效削弱了喇叭口下方附底涡强度，高涡量区域明显缩小，且减小了后壁面产生的附壁涡。

4 结 论

应用计算流体力学（Computational Fluid Dynamics，CFD）技术，基于响应曲面模型研究了底坎相对高度、相对距离与泵站进水流态之间的函数响应关系得出以下结论：

1）信息量权数法可对泵站进水系统内速度场和涡量场的多个评价指标进行赋权，形成综合目标函数来定量表示底坎整流措施对泵站流态的改善效果。

2）以底坎相对高度、距离为设计参数，进行响应曲面优化分析，拟合三次多项式响应面模型的函数关系式，综合目标函数的R2为0.86，均方根误差为0.02，模型具有较高精度。基于响应曲面拟合结果，采用最速下降法求解的底坎整流措施最优参数组合的相对坎高为0.29，相对坎距为5.02，所计算的综合目标函数实际值与估算值相对误差为1.30%，表明所采用的三次多项式响应面模型能准确描述底坎整流措施设计参数与综合目标函数之间的关系。

3）基于最佳参数组合对底坎坎高和坎距进行优化，并模拟泵站水力性能，结果表明，优化后泵站流速不均匀系数减小19.28%，计算域水力损失系数减小5.26%，喇叭口涡量特征值降低了5.76%。底坎优化方案前池两侧回流区基本消失，各个进水池水流进流平顺，吸水管附近漩涡强度明显减小，进水建筑物内流态得到显著改善。表明响应曲面模型可用于泵站整流措施参数优化设计，改善前池、进水池流态，提高泵站的水力效率和运行稳定性。

本文仅以整流底坎的坎高和坎距2个设计参数进行优化，但是，前池整流措施形式多样，且存在组合应用，后续可对其他组合形式的整流措施进行更多设计参数的优化分析。