基于采样数据的一阶多自主体系统的平均一致性跟踪

顾晓雨,李 力

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

作为多自主体系统分布式协调控制中的最重要和基础的问题，多自主体系统的一致性问题因为其在多个领域的广泛应用而备受关注。多自主体系统的一致性问题主要应用于分布式估计、传感器网络的数据融合、无人机的编队控制、计算机网络的资源分配[1]等。一致性，即自主体通过与邻居自主体相互通信交换信息，最终所有自主体的状态都达到一致。已有的文献从自主体的模型、时延、拓扑结构、控制策略等角度研究了多自主体系统的一致性[2]。

本文中研究的平均一致性跟踪问题要求所有自主体的最终状态跟踪自主体参考输入的平均值。平均一致性跟踪问题显然不同于平均一致性问题，传统的平均一致性问题要求自主体最终状态收敛到自主体初始状态的平均值。Freeman[3]等分别比较了针对解决静态平均一致性跟踪问题的比例平均一致性算法和解决动态平均一致性跟踪问题的比例积分平均一致性算法，并得出结论：比例积分算法对于常数参考输入和变化缓慢的参考输入具有更好的效果。受文献[3]的启发，Bai[4]等分析了针对常数参考输入的比例积分平均一致性跟踪算法的结构特点，并利用内部模型原理将比例积分平均一致性算法拓展到更一般的情况，使自主体可以跟踪几类时变的参考输入。对于具有常数参考输入的一阶多自主体系统，Shan和Liu[5]考虑了部分自主体缺少参考输入的平均一致性跟踪问题，并给出了相应的算法。利用广义奈奎斯特判据，分别给出了在对称连通拓扑下，自主体有无通信时延的收敛条件。Shao和Tian[6]针对具有非匹配参考输入的一阶多自主体系统提出了平均一致性跟踪算法，但是该算法要求所有自主体知道自主体的数量以及所有的参考输入。

在实际应用场景中，自主体常常因为间歇通信和受限的感知能力而只能周期性地相互通信，最终导致离散或者采样数据的情况。基于采样数据的一致性问题引起了研究者的广泛兴趣，并应用代数图论、矩阵论和随机矩阵的性质等方法研究了各种限制情况下的一致性问题。现有的研究结果表明，采样数据控制策略不仅可以极大地减少通信损耗，还可以提高系统对于由系统连接故障和传输时延引起的切换拓扑的鲁棒性。然而，基于采样数据的一致性跟踪效果与采样间隔密切相关。

受前人研究的启发，我们提出并分析了2种情况下的基于采样数据控制的比例积分平均一致性跟踪算法。第1种情况是所有自主体都具有常数参考输入，第2种情况是部分自主体有常数参考输入而剩下的自主体没有常数参考输入。利用矩阵论的知识，给出了第1种情况在平衡拓扑下收敛到平均一致性跟踪的充要条件。相应地，针对第2种情况，运用频域分析的方法给出了连接拓扑为无相连通拓扑下渐进达到平均一致性跟踪的充分条件。

1 问题描述

1.1 自主体模型

本文研究的一阶自主体系统的模型如下：

(1)

式中：xi(t)∈R和ui(t)∈R分别是自主体i的状态和控制输入。

本文的目标就是设计一种控制算法，使得对于任意的参考输入φi,i=1,2,…,n，有：

(2)

即所有自主体渐进达到平均一致性跟踪。

1.2 需要引理

引理1：对于n阶方阵M，N，P，Q，如果MP=PM，那么：

(3)

引理2：对于如下的复系数多项式：

g(s)=s2+(ξ1+iσ1)s+ξ0+iσ0

(4)

式中：ξ1，σ1，ξ0和σ0为常实数。

当且仅当ξ1>0和ξ1σ1σ0+ξ12ξ0-σ02>0成立时，g(s)是稳定的。

2 主要结论

2.1 匹配参考输入的平均一致性跟踪

在许多应用场景中，因为数字传感器和基于计算机的控制，尽管自主体的模型是连续的，自主体的控制器只有在离散采样时刻获得采样数据。为了实现平均一致性跟踪，考虑一种在离散采样时刻获得采样数据并且控制输入是基于零阶保持器的平均一致性跟踪算法。假设采样周期是T=tk+1-tk，提出如下的分布式算法：

(5)

式中：φi∈R和ηi∈R是自主体i的常数参考输入和内部状态；在平均一致性跟踪算法(4)中，ηi(t)的作用是消除自主体的跟踪误差；γ>0，kP>0和kI>0是控制增益；xi(tk)和xj(tk)均为在采样时刻tk获得的状态信息。

(6)

其中f(t)定义如下:

f(t)=kIθi(tk)(t-tk)+ω

(7)

通过计算得到在算法(4)下的多自主体系统(1)的闭环形式为：

(8)

(9)

接下来,针对基于采样数据的模型(8)，给出相应的结论。

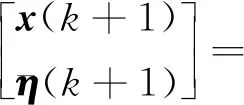
(10)

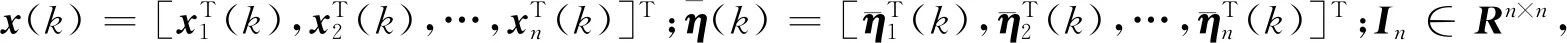
接下来，推导多自主体系统在平衡且强连通拓扑下达到平均一致性跟踪的条件。

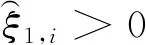
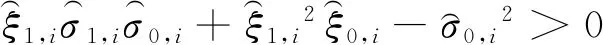
证明：首先分析一阶多自主体系统(9)的收敛性。

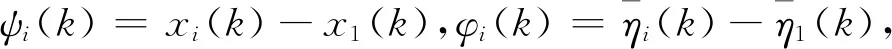
令ψ(k)=[ψ1(k),…,ψn(k)]T，φ(k)=[φ1(k),…,φn(k)]T，z(k)=[ψT(k),φT(k)]T，可得：

z(k+1)=Δz(k)

(11)

式中：

对拉普拉斯矩阵L进行基本行变换和列变换：

(12)

下面分析下列方程的根的情况:

det(λI2n-2-Δ)=0

(13)

根据引理1，式(12)等价于：

det{(λ-α)(λ-1)In-1+[β(λ-1)·(1-α)+

(14)

方程(14)等价于：

(1-α)+kIT(λ-1)+kI(1-α)T]}=0

(15)

接下来，考察下列方程的根：

(λ-α)(λ-1)+[β(λ-1)(1-α)+

(16)

(17)

根据引理2，当且仅当定理1中的(1)和(2)成立时，方程(17)的根都在左半复平面，即在连接拓扑满足假设1的情况下，一阶多自主体系统渐进达到平均一致性跟踪。

第2步，证明最终达到一致的决策值是常数参考输入的平均值。由先前的证明可知，一阶多自主体系统已经渐进达到了一致，即当k→∞时，x1(k)=x2(k)=…=xn(k)，对于i=1,…,n，有：

(18)

即:

(19)

可以得到：

(20)

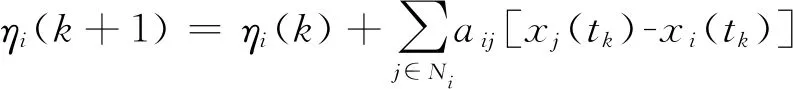
η1(k)+η2(k)+…ηn(k)=η1(0)+η2(0)+…ηn(0)

(21)

2.2 非匹配参考输入的平均一致性跟踪

在实际工程应用场景中，多自主体系统中只有部分自主体获得了参考输入，而剩余的自主体没有参考输入。Shan和Liu[5]研究了连续通信中一阶多自主体系统的平均一致性跟踪问题，所以我们在这部分研究了在采样数据控制下的情形。

针对第2种情况，将算法(4)修改成了如下形式：

(22)

其中当i=1,…,m时，δi=1；而当i=m+1,…,n时，δi=0。控制目标表示如下：

(23)

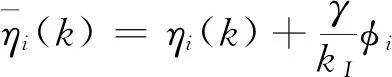
(24)

(25)

得到上述系统的特征方程：

(26)

(27)

(28)

证明：根据引理2和文献[5]中定理1的证明，方程(19)在z=1处有1个单根。当z≠1时，通过计算可得：

令：

(29)

需要证明F(z)根的模都小于1。根据文献[7]中的广义奈奎斯特判据，如果对于ω∈(0,π)，ρ(L)Co(0∪gl(ω),l=1,2)没有包含(-1,j0)点，则F(z)的零点都在以原点为中心的单位圆内。对于对称图，根据拉普拉斯矩阵的定义，可知L=LT≥0。根据文献[8]中的引理4，可以得到：

ρ(L)Co(0∪gl(ω),l=1,2

(30)

如果ρ(L)Co(0∪gl(ω),l=1,2)没有包含(-1,j0)点，F(z)的零点除了1个在z=1以外，其余的根都在以原点为中心的单位圆内。剩下的证明过程类似于定理1，在此不再赘述。

3 仿真实例

在这部分，提供了数值仿真以验证前面得到的理论结论的有效性。

首先考察了第1种情况由4个自主体构成的一阶多自主体系统，其通信拓扑是平衡且强连通的，如图1所示。

图1 平衡且强连通拓扑

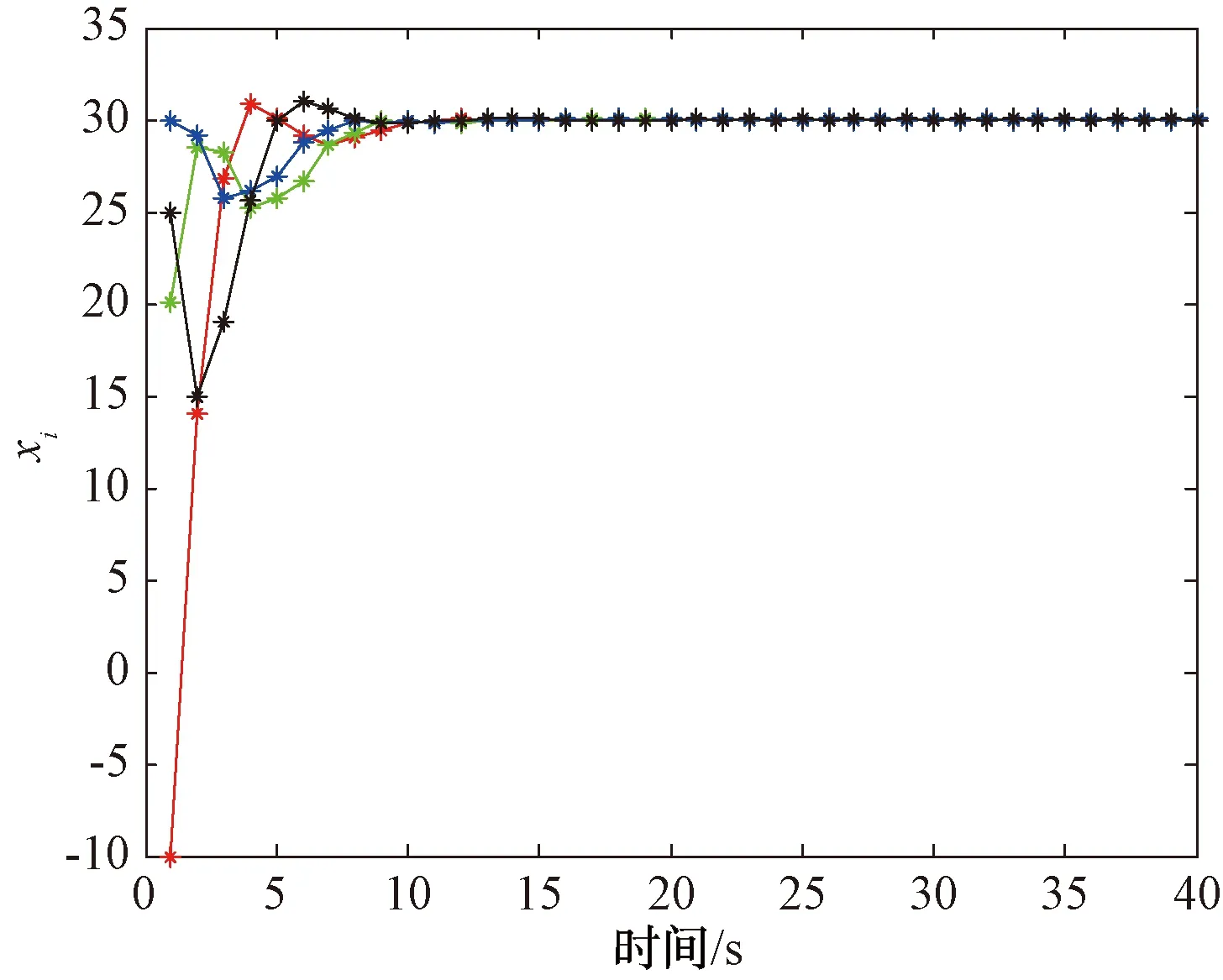
图2 自主体的位置

接下来考察第2种情况中由4个自主体构成的多自主体系统，其通信拓扑是对称连通拓扑，见图3。

图3 对称连通拓扑

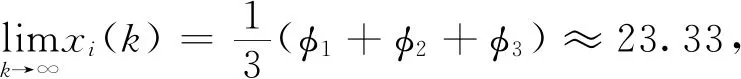
图4 自主体的状态

图5 奈奎斯特曲线ρ(L)Co(0∪gl(ω),l=1,2)

4 结束语

本文对于具有常数参考输入的一阶多自主体系统提出了基于采样数据的比例积分平均一致性跟踪算法。首先运用矩阵论和图论的知识论证并给出了多自主体系统在平衡且强连通拓扑下达到平均一致性跟踪的充要条件。然后针对部分自主体缺少参考输入的情况，提出了改进的平均一致性跟踪算法，并根据频域分析方法给出了多自主体系统在对称连通拓扑下达到平均一致性跟踪的充分条件。