数形结合思想在初中数学教学中的应用
2021-04-14郭礼军
郭礼军
(江苏省高邮市汪曾祺学校 225600)
数学知识具有一定的抽象性,这也是导致数学教学存在难度的关键.和小学阶段数学相比较,初中阶段数学教学的知识量更多,对于学生来说,学习的难度也明显加大.在这种情况下,学生很容易在数学学习中出现问题,影响学习效率.因此,初中数学教师就需要研究新的教学思想和方法,将数形结合思想融入教学中,直观的将数量关系和空间关系呈现在学生面前,降低学生学习的难度,还能加深学生对数学知识的理解和运用.
一、数形结合思想在初中数学教学中的应用作用
1.更容易理解数学概念
在初中数学教学中,数轴作为一种基本学习工具,在教学中占据着重要地位.在数学概念的理解上,应用数轴,能够让数学问题更加直观和形象,能够引导学生理解绝对值、相反数等数学知识.例如,将数轴原点为基准点,两侧的数字互为相反数,这样学生就很容易理解相反数的相关知识.
2.更容易解决几何问题
初中数学的几何知识和代数计算属于相互融合的关系,比如,相似三角形、锐角三角形等课程的学习,学生不仅要能够正确理解这些概念,而且还要结合题目中给出的条件进行问题计算.比如三角函数、勾股定理等都是解决几何问题的方式.这也是一种数形结合方式,选择合适的代数知识解决几何图形问题.
3.更容易学习函数
对于函数的学习来说,需要有图形知识的支撑.一般在遇到函数问题时,假如只利用给出的条件进行计算很难顺利解决问题,即便得出正确答案,解答过程也十分繁琐.然而,可以采用图形的方式,采用建立坐标系、画一次函数、二次函数等图像的方式,提升函数问题解答的便捷性,还能让数学问题更加直观,在一定程度上起到培养学生问题分析和处理的能力.
二、数形结合思想在初中数学教学中的应用方式
1.数学概念中应用数形结合思想
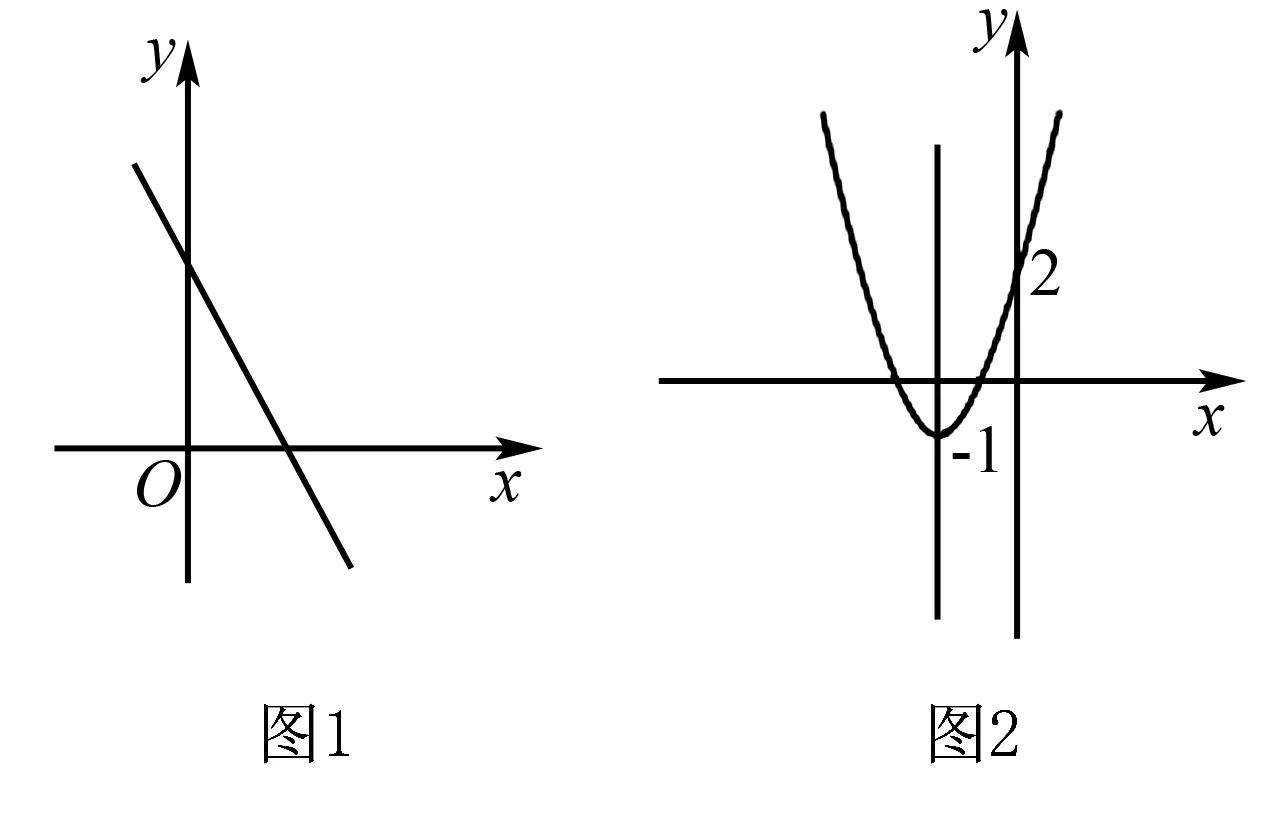
在初中数学教学中,概念是知识学习的基本形式,每一个概念都是对数学知识的抽象概括,在数学概念教学中应用数形结合思想,能够帮助学生更好的理解,能够感知和接受数学知识.例如,在教学一次函数的概念时,将一次函数定义为形如y=kx+b的式子,其中k、b为常数,且k≠0,这个式子称y是x的一次函数.在对学生讲解一次函数的性质时,可以为学生提供一次函数的图像,如图1所示,可以引导学生在一次函数图像的基础上,感受函数y随着自变量x增大而发生的变化.同时,还可以让学生深入进行理解,分析当自变量x从某一数值变化到另一数值时,y的值会发生怎样的变化.这样设置图形能够让学生更容易理解抽象、难懂的数学概念和形式.采用数形结合思想,让学生对知识的本质进行思考.例如,在教学等式的性质时,根据教材内容,了解到等式的形式为等式两边的式子同时加上或者减去同一个数字或者式子时,结果还是相等.因此,在教学过程中可采用天平的原理,将两个式子分别放在天平的两端,这样学生很容易理解等式性质,并将其运用于解题中.
2.在问题解决中应用数形结合思想
(1)在函数问题中的应用
在初中函数教学中,采用数形结合思想,能够让抽象的函数和直观的图像结合起来,让学生更容易理解问题.在初中数学教学中,函数知识的覆盖面较为广泛,要求学生全面掌握函数相关知识,很容易导致学生在学习中产生抵触心理,对于这种情况的存在,教师可以根据函数和图形之间的联系,引导学生画出正确的坐标系,并从问题上找出关键点,做出图像,顺利解决问题.
例如,在教学二次函数之后,学生都了解二次函数的开口方向取决于a值的正负,其中c值决定和y轴交点纵坐标的值,a和b共同决定了函数图像的对称性,以此为基础,可以为学生提出这样一个问题,让学生根据数形结合思想解决.例如,已知函数y=ax2+bx+c(a,b,c为常数,a≠0)图像上,有坐标为(-1,y1)、(-3,y2)、(2,y3)的三点,则试探究y1、y2、y3的值的大小关系.从题目中可以分析出该题主要是为了判断二次函数值的大小关系,假如学生在解决问题的过程中,将坐标值带入函数中,必定会增加计算量,增加问题的难度.在这种情况下,教师可以引导学生采用数形结合的思想,先将该函数图像画出来,这样就能够对比出y1、y2、y3的值的大小关系.如图2所示,当x=-1时,y1值最小,当x=2时,y3值最大,当x=-3时,y2值小于y3大于y2,因此可以得出y1 (2)在不等式组问题中的应用 通常数学知识中等式方程组和不等式组之间存在较大的差异,等式方程可以在等式方程组中实现符号随意转换,而不等式在不等式组中无法实现符号随意转换.因此,不等式组的解答难度更大.因此,在解答不等式组的问题中,可以先将不等式组进行分解,并且利用数形结合的方式,引导学生利用数轴进行解答. 例如,求2x-1≥x+1;x+8≤4x-1.在解答该不等式组时,学生需要先将两个不等式的解分别求出,也就是前者为x≥2,后者为x≥3,但是这并不是该不等式组的最后解,需要采用数形结合的方式,根据求出的不等式的解,画出相应的数轴,再借助数轴,准确的找出两个不等式之间的共同解集部分,该部分才是不等式组的解集.需要注意的是,在绘制数轴的过程中,要注意“>”和“<”的方向,画出正确的数轴,这样才能得出正确的答案. 3.在复习归纳中应用数形结合思想 在学习完数学知识之后进入复习阶段,可以将各个知识点中存在的数形结合思想方式概括出来,这样能够显著提升学生数形结合思想的应用意识,进而提升独立分析、思考和解决问题的能力.比如,利用数形结合解决不等式、关系式问题,利用图形的几何特性、代数含义解决平面图形相关问题,利用函数关系式、图像解决一次函数、二次函数问题,利用直角坐标系解决线段、图形问题等等,进而将复杂的问题简单化,还能让学生将学到的概念、性质等知识融入问题中,建立数形结合思想,进而逐渐解决问题.在复习归纳中,对可以采用数形结合思想的问题进行总结,能够进一步提升学生的学习能力和解决问题的能力,拓宽学生的思维,让学生在空间图形结构中,对数学问题进行探索. 总之,对于初中数学教学来说,各种知识具有较强的抽象性和逻辑性,学生学习起来具有一定的难度.数形结合思想是一种解决数学问题的主要思想,也就是将“数”和“形”结合起来进行数学问题解决的一种思想,通过“数”“形”转换,能够帮助学生更深入的理解知识.经过相关实验表明,将数形结合思想应用于数学概念教学、数学问题解决以及复习归纳中,能够有效提升学生的学习效率,发挥数形结合的价值.
