基于熵权TOPSIS法的CFRP防撞梁轻量化研究*
2021-04-14蒋荣超孙海霞刘大维陈焕明王登峰
蒋荣超,张 涛,孙海霞,刘大维,陈焕明,王登峰
(1. 青岛大学机电工程学院,青岛 266071;2. 海军航空大学青岛校区航空机械系,青岛 266041;3. 吉林大学,汽车仿真与控制国家重点实验室,长春 130022)
前言
汽车轻量化是实现节能减排的重要途径,结构优化设计、采用先进制造工艺和应用轻质材料等轻量化技术已成为汽车领域的研究热点[1-3]。在轻量化材料中,碳纤维增强复合材料(carbon fiber reinforced plastic,CFRP)因其具有较高的比强度、比刚度和优异的吸能特性,尤其适合于电动汽车结构件的轻量化[4-5],是汽车轻量化技术的重点研究方向,得到了国内外学者的广泛关注。叶辉等[6]对碳纤维复合材料发动机罩进行了铺层优化设计,结果表明CFRP 发动机罩能在保证其力学性能的同时充分发挥其在汽车轻量化方面的优势。顾善群等[7]通过高速冲击试验和压缩性能测试研究了复合材料的破坏模式与冲击速率和树脂韧性之间的关系。陈光等[8]采用刚度等效替代方法和正向设计方法对碳纤维复合材料保险杠进行尺寸优化,在保证吸能要求的前提下实现了保险杠总成的轻量化。Hu 等[9]对比研究了碳纤维增强复合材料保险杠横梁与钢制横梁的吸能性,研究表明CFRP 保险杠横梁具有更优异的吸能特性。
保险杠是汽车被动安全系统的关键部件,主要由防撞梁、吸能盒和填充物组成,其中保险杠防撞梁是低速碰撞过程中的主要吸能结构,可以起到有效的缓冲作用,减轻对行人与乘员的伤害和对车辆的损伤[10-12]。目前国内外学者通过结构优化和应用新材料等方法,对汽车保险杠开展了较多研究。曹立波等[13]基于试验设计优化方法对铝合金横梁壁厚进行优化,提高了保险杠耐撞性和行人保护性能。徐中明等[14]采用材料替换和结构优化方法设计了铝合金防撞梁,通过有限元仿真和三点静压试验对比分析了钢制防撞梁和铝合金防撞梁的耐撞性能。高云凯等[15]基于混合元胞自动机方法和Kriging 近似模型技术对铝合金保险杠横梁进行耐撞性拓扑优化,提高了保险杠横梁耐撞性且实现了轻量化。李旻等[16]通过有限元仿真对比分析了不同厚度保险杠系统的动态响应特性和能量变化情况。童小伟等[17]基于近似模型和遗传算法通过铺层优化设计提高了CFRP 保险杠的安全性能,并显著减轻了质量。Park等[18]以耐撞性和行人保护性能为目标,基于响应面建模技术对保险杠进行了形状优化。
本文中以某汽车保险杠防撞梁为研究对象,充分利用CFRP 材料良好的可设计性和优异的力学性能,研究CFRP 防撞梁轻量化设计方法。首先通过CFRP层合板力学性能试验获得材料参数,利用层合板三点弯曲性能试验进行验证。然后将保险杠原钢质防撞梁用CFRP 材料替代,并通过有限元仿真对比分析两种材料防撞梁的抗撞性能。在此基础上,基于汽车抗撞性要求,采用正交试验设计和熵权TOPSIS 法对保险杠CFRP 防撞梁进行铺层优化,获得最优铺层方案,实现CFRP防撞梁的轻量化设计。
1 碳纤维复合材料力学性能试验
1.1 CFRP层合板力学性能试验
选取T300 斜纹机织碳纤维布和E51 环氧树脂,利用真空辅助成型工艺在室温下固化24 h 后脱模,得到CFRP 层合板,并制作用于CFRP 力学性能试验的标准试样。拉伸试验样件为单向层合板,面内剪切试验样件为±45°层合板,均由8 层碳纤维布制成,厚度为1.92 mm,压缩试验样件是由16 层碳纤维布制成的3.86 mm 厚单向层合板。为获得CFRP 力学参数,参考标准ASTM D3039/D3039M-14、ASTM D3518/D3518M-13 和ASTM D6641/D6641M-09,采用电子万能试验机分别对CFRP 层合板试样进行单向拉伸、面内剪切和压缩力学性能试验,速率分别设置为2、2 和1.3 mm/min,其中拉伸试验过程如图1所示。每种试验均选取5个试样,根据5次重复试验测得的数据,计算每个性能的平均值、标准差和离散系数(标准差和平均值的比值)。如离散系数值过大,须将样本中可疑的测量值剔除后再计算平均值,将各性能平均值确定为CFRP 力学参数,如表1所示。

图1 CFRP层合板力学性能试验

表1 CFRP力学参数
1.2 三点弯曲性能试验验证
利用所测CFRP 力学性能参数构建CFRP 层合板三点弯曲有限元模型,试样采用0.5 mm×0.5 mm的壳单元离散,压头和支座的网格单元尺寸为1 mm,共计4 484 个单元,如图2 所示。压头和支座在试验过程中不发生变形,选取刚体材料MAT20 进行模拟。CFRP 层合板试样选择MAT54 材料模型,采用Chang-Chang 准则进行失效判断。为更准确模拟复合材料失效过程,除力学性能参数外,MAT54 材料模型还考虑了渐进失效参数,如表2 所示。当某单元所有铺层都达到失效状态时,删除该单元,且其相邻单元强度会折减。MAT54 材料模型大部分参数可通过材料试验获得,但其渐进失效参数须通过不断调整,直到三点弯曲仿真曲线能较好地拟合试验曲线[19]。

图2 三点弯曲有限元模型

表2 材料渐进失效参数
参考标准ASTM D7264选取T300 斜纹机织碳纤维布制作CFRP 层合板试样,并对试样进行三点弯曲试验,如图3 所示。将试样放在两支座中间,压头以2 mm/min的速度向下移动。考虑到试验误差的影响,试验次数不低于5次。

图3 三点弯曲试验
CFRP 层合板试样在压力作用下发生弯曲变形,连续加载至试件破坏,记录载荷-位移数据,试验与仿真结果对比如图4所示。
从图4 可以看出,CFRP 层合板三点弯曲工况下有限元仿真和试验失效模式较为相似,试验测量与仿真计算的载荷-位移曲线也较为接近,所建CFRP失效模型可用于汽车保险杠CFRP 防撞梁的抗撞性能分析。

图4 三点弯曲试验与仿真结果对比
2 保险杠CFRP防撞梁初始设计
2.1 CFRP防撞梁厚度设计
为使CFRP 防撞梁能安装在原车型上,其尺寸和结构与原钢制防撞梁相同,仅将防撞梁金属材料替换为CFRP。在材料替代过程中,须对防撞梁厚度进行修改以保证结构刚度不变。根据等刚度设计理论,结构刚度与板件厚度的关系受材料弹性模量和零件尺寸与载荷工况的影响[20]。薄板件结构刚度与厚度的关系可近似描述为

式中:K为薄板件结构刚度;β(λ)为零件形状与载荷工况系数;E为材料弹性模量;t为薄板件厚度;λ为厚度指数,对于汽车结构,λ一般取1~3。
在保证刚度不变的前提下,CFRP防撞梁厚度计算公式为

式中:t0和t1分别为材料替换前后的厚度;E0为钢的弹性模量;E1为CFRP弹性模量。
原钢制防撞梁厚度为2 mm,根据等刚度近似关系,利用两种材料的弹性模量,初步估测CFRP 防撞梁厚度为3.6 mm,此时厚度指数λ取值2.38,防撞梁质量由6.6降低为2.29 kg,减轻了65.3%。
2.2 低速碰撞有限元建模
保险杠低速碰撞模型中将车身简化,仅保留防撞梁和吸能盒,采用壳单元将模型划分为8 963个单元和9 133 个节点,建立保险杠低速碰撞模型如图5所示。

图5 保险杠低速碰撞有限元模型
基于经典层合板理论对保险杠CFRP 防撞梁进行有限元建模,为简化设计和提高效率,层合板铺层设计时通常采用0°、45°、-45°和90°4 个典型铺层角度。因此,CFRP 防撞梁初始铺层设计采用24 层厚度为0.15 mm的单层板,铺层顺序确定为[0°/45°/-45°/90°]6,如图6所示。
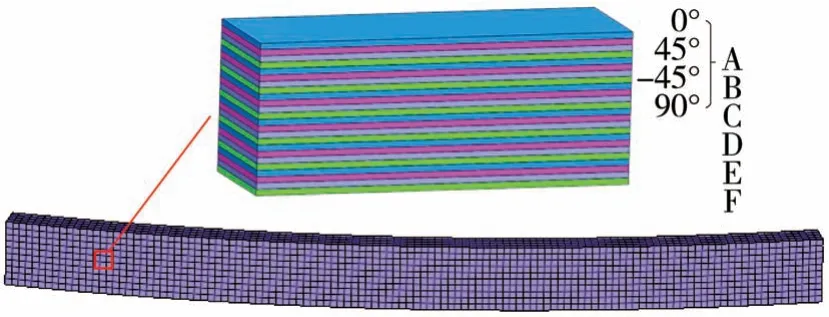
图6 CFRP防撞梁铺层
2.3 防撞梁低速碰撞抗撞性能分析
保险杠低速碰撞有限元模型中通过质量单元模拟整车质量,并与保险杠系统进行连接,设置保险杠系统初始速度为4 km/h 进行正面低速碰撞仿真,两种材料的仿真结果分别如图7 和图8 所示。可以看出,两种防撞梁的变形均主要发生在防撞梁中间位置和防撞梁与吸能盒的连接部位,其中钢制防撞梁主要发生弹性变形;仅在防撞梁与吸能盒连接位置处有少量塑性变形,CFRP 防撞梁两端与吸能盒连接处均出现网格删除,说明该处发生失效破坏。此外,两种防撞梁碰撞过程中系统总能量守恒,能量曲线并无突变,沙漏能分别占总能量的0.23%和1.16%,均在5%以内,仿真结果具有较高的准确性。
汽车保险杠防撞梁的抗撞性能通常采用吸能量(比吸能)、最大侵入量和碰撞力峰值来评价,三者反映了防撞梁通过变形将动能转化为内能并有效保护乘员安全的能力,以及对乘员和车辆结构的危害程度。根据有限元分析结果,得到两种材料防撞梁的吸能量、比吸能、侵入量和碰撞力的时间历程曲线如图9~图12所示。

图7 钢制防撞梁碰撞分析结果
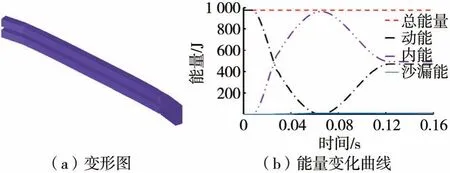
图8 CFRP防撞梁碰撞分析结果

图9 防撞梁吸能量对比
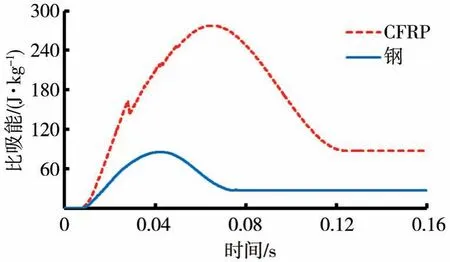
图10 防撞梁比吸能对比
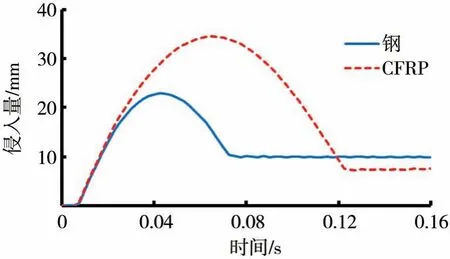
图11 防撞梁侵入量对比
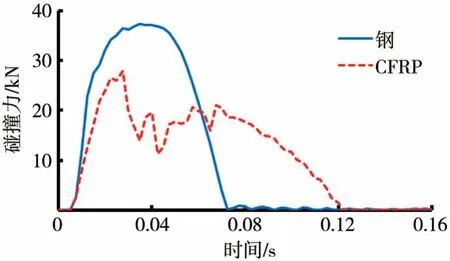
图12 防撞梁碰撞力对比
从以上图中可以看出,CFRP防撞梁的吸能量略大于钢制防撞梁,但由于两种材料质量的差异,CFRP防撞梁比吸能远大于钢制防撞梁,吸能效果更好;CFRP 防撞梁的侵入量要大于钢制防撞梁,两者的最大侵入量分别为34.13 和23.54 mm,满足使用要求;CFRP 防撞梁碰撞力小于钢制防撞梁,说明防撞梁材料由钢材替换为CFRP 后,抗撞性能得到一定改善。
3 CFRP防撞梁铺层优化设计
3.1 CFRP防撞梁单目标铺层优化
基于正交试验设计方法,将图6 中CFRP 防撞梁铺层中A、B、C、D、E、F 分区和单层板厚T定义为正交试验设计的7 个因素,每个因素设置3 个水平,其中A、B、C、D、E、F 6个分区分别选取3种经典铺层[0°/45°/-45°/90°]、[45°/-45°/0°/90°]、[0°/45°/90°/-45°]作为因素的1、2、3 水平,厚度选取[0.1 mm]、[0.15 mm]、[0.2 mm]作为因素的1、2、3 水平,采用正交表L18(37)安排仿真分析,仿真工况如表3所示。
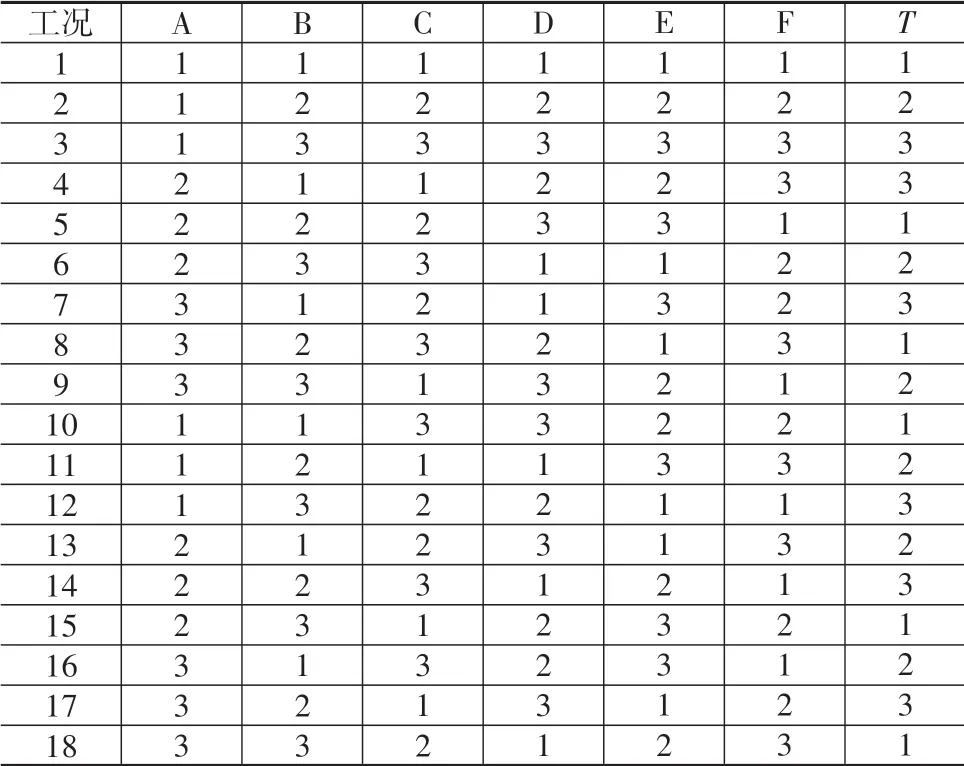
表3 CFRP防撞梁仿真工况
考虑到抗撞性和轻量化的要求,选取质量、比吸能、最大侵入量和碰撞力峰值作为CFRP 防撞梁的性能评价指标,通过低速碰撞仿真分析,计算得到18 种铺层方案CFRP 防撞梁的性能指标,仿真结果如图13所示。
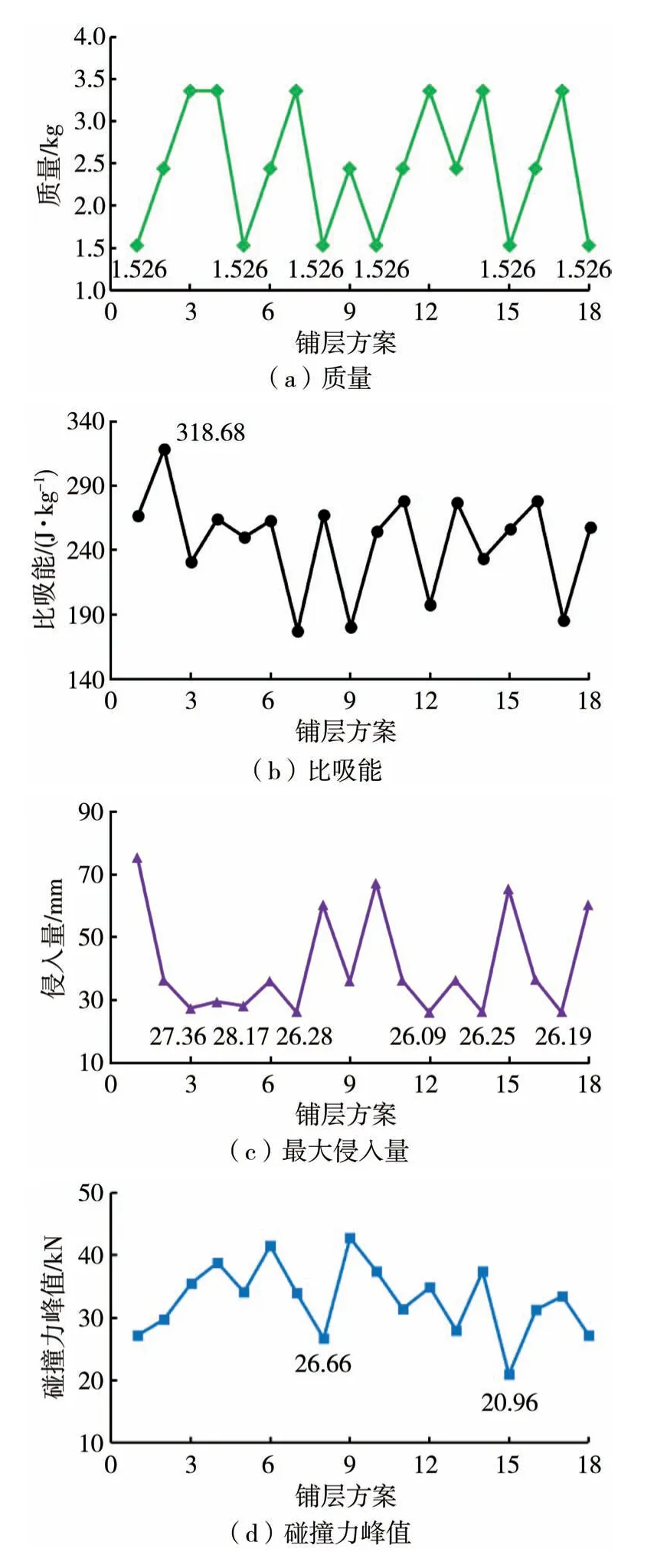
图13 CFRP防撞梁性能指标仿真结果
由图13可以看出,对于质量指标,显然单层厚度为0.1 mm 的方案为最优铺层方案;对于比吸能指标,铺层方案2的比吸能值最大;铺层方案12的最大侵入量指标值最小,铺层方案15的碰撞力峰值最小。因此,针对不同性能指标铺层优化方案也不相同,为确定使每个性能指标都尽可能好的铺层方案,须进行多目标综合优化分析。
3.2 基于熵权TOPSIS的多目标铺层优化
TOPSIS 方法可将多指标评价问题转化为单个综合指标评价问题进行研究[21],将18 种铺层方案的CFRP 防撞梁的性能指标定义为TOPSIS 方法中的决策矩阵,可表示为
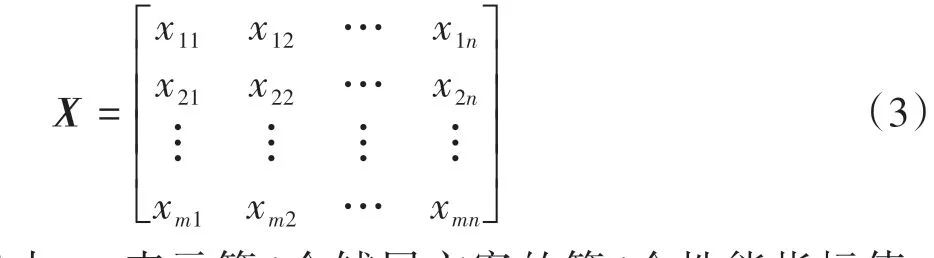
式中:xij表示第i个铺层方案的第j个性能指标值,i= 1,2,…,m;j= 1,2,…,n;m为铺层方案个数;n为性能指标数量。
为消除量纲的影响,对决策矩阵进行正则化处理,计算公式为

式中rij为xij正则化处理后的结果。
CFRP防撞梁各性能指标的重要程度往往不同,可采用熵权法计算其权重系数,计算公式为

式中:wj为第j个性能指标的权重系数;表示第j个性能指标的信息熵;k=1/ln(m)为调节系数;为对rij规范化处理的结果。采用熵权法对各性能指标进行客观赋权,计算得到各指标权重系数,如表4所示。
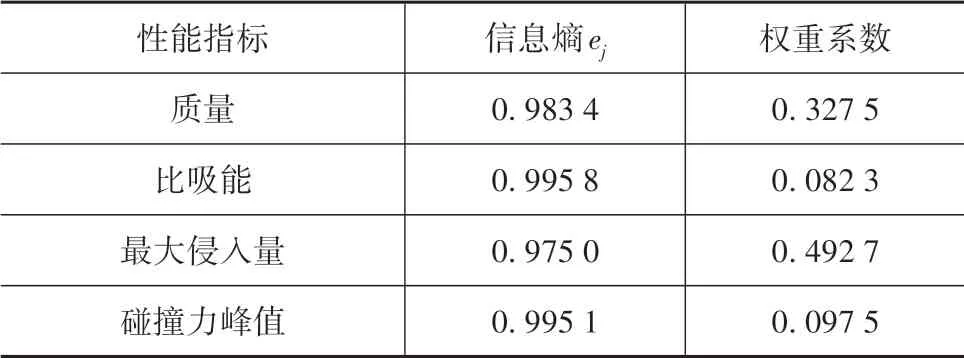
表4 防撞梁性能指标权重系数
对正则化的决策矩阵rij进行加权,得到新的决策矩阵vij:
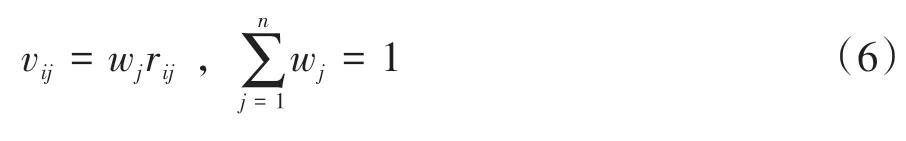
TOPSIS 方法通过计算每个参数与理想解和负理想解的距离对其进行排序,理想解和负理想解可定义为

式中A+和A-分别表示理想解集和负理想解集。
CFRP防撞梁质量、最大侵入量和碰撞力峰值是越小越好,其理想解和负理想解计算公式为
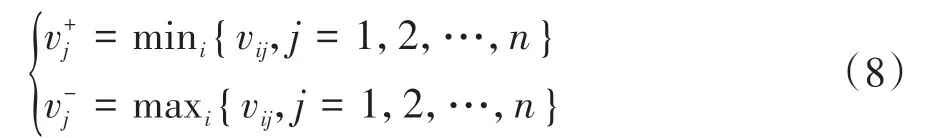
式中和分别表示第j个性能指标的理想解和负理想解。
对于CFRP 防撞梁比吸能指标,则是越大越好,因此,其理想解和负理想解计算公式为

每个铺层方案与理想解和负理想解之间的距离可使用欧氏距离计算,即
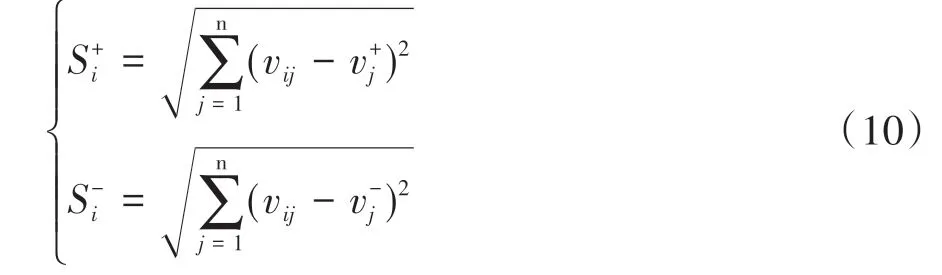
式中和分别为第i个方案与理想解和负理想解的距离。
每个方案与负理想解的相对接近程度可定义为相对接近度系数,并以此作为综合评价指标,可确定出最优方案。相对接近度系数计算公式为

式中Ci为第i个铺层方案的相对接近度系数,其数值越大,说明该铺层方案的CFRP防撞梁性能越好。
基于熵权TOPSIS 方法计算每种铺层方案与负理想解的相对接近程度,并根据相对接近度系数进行排序,从而确定出最优铺层方案,18 种铺层方案的相对接近度系数计算结果如图14 所示。各铺层方案的相对接近度系数综合考虑了质量、比吸能、最大侵入量和碰撞力峰值,反映了不同方案的抗撞性能和轻量化水平,因此确定出第5组为CFRP 防撞梁最优铺层方案。
3.3 优化结果分析
将钢制防撞梁和优化后CFRP 防撞梁的各项性能指标进行对比分析,结果如表5所示。

图14 各铺层方案的相对接近度系数
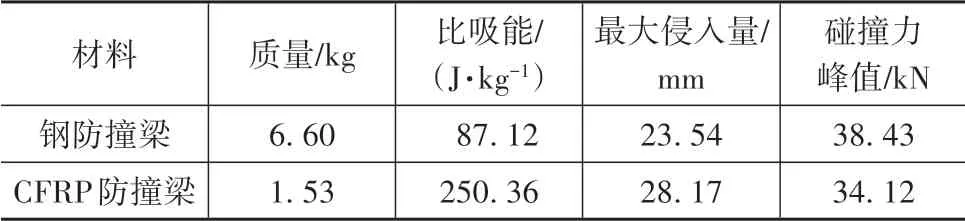
表5 防撞梁轻量化前后性能对比
由表5 可知,防撞梁的质量由钢制的6.60 kg 降低到优化后CFRP 的1.53 kg,减轻76.82%,轻量化效果显著;比吸能提高了1.87 倍;碰撞力峰值下降了11.2%,最大侵入量略有增大,但仍满足设计要求。
4 结论
(1)采用斜纹机织碳纤维布制作了CFRP 层合板试样,通过力学试验获得了CFRP 力学参数,并利用CFRP 层合板三点弯曲性能有限元仿真和试验对材料参数进行了验证。
(2)基于等刚度设计理论将保险杠原钢制防撞梁替换为CFRP,并通过保险杠低速碰撞有限元仿真对比分析了两种材料防撞梁的抗撞性能。
(3)综合考虑质量、比吸能、最大侵入量和碰撞力峰值等因素,利用正交试验设计和熵权TOPSIS 方法对CFRP 防撞梁进行铺层优化,获得了最优铺层方案。
(4)优化后的CFRP 防撞梁在满足抗撞性能要求的情况下,比原钢制防撞梁减轻了76.82%,取得了较好的轻量化效果,为轻质高强的防撞梁结构设计提供了参考。
