基于驾驶风格的前撞预警系统报警策略*

金 辉，李昊天

（北京理工大学机械与车辆学院，北京 100081）

前言

每年公路交通安全问题都会导致大量的人员伤亡，酒驾、驾驶疲劳、驾驶经验不足等都可能导致交通事故，追尾是常见的交通事故之一。追尾的直接原因是驾驶员无法正常处理前后车关系，前后车纵向间距过小以致无法躲避，最终造成事故。不同驾驶员风险感知能力不同、操作习惯不同，则可能有不同的驾驶风格，研究表明道路安全性与驾驶风格有很大关系［1］。前撞预警系统可以在事故发生前提醒驾驶员，避免意外发生，但当前的前撞预警策略大都无法适应于不同驾驶风格，这导致了更多的误报警，也降低了人们对系统的接受程度。因此，在考虑驾驶风格情况下改进预警策略的研究很有意义。

道路驾驶的安全性与驾驶员的驾驶风格十分相关。受到不同交通文化影响的人在道路安全方面也表现不同，他们有不完全相同的驾驶行为准则［2-3］。研究人员开发了许多高级驾驶辅助系统，以提高驾驶安全性，减轻驾驶员负担。文献［4］中分别针对直道、弯道和交叉路设计了多种前撞预警策略，定义了风险因子，提出了一种前撞预警功能的检测方法。不同驾驶风格的人可能会有不同的可接受车头间距和碰撞时间，这些量的阈值常是辅助驾驶系统的关键参数。而在系统中，这些参数比较固定，无法适应每个人的驾驶风格，由此产生的误报警降低了人们对驾驶辅助系统的接受程度［5-9］。

传统的前撞预警策略主要有两种，分别基于预警距离和碰撞时间。文献［10］中提出了一种以防撞最小减速度为风险指标的算法。算法主要研究两种交通情况，即前车加速度不变下预警和前车急减速下预警。试验结果表明基于减速度的前撞预警系统可以有效避免碰撞，且大部分试验对象表示防撞最小减速度比碰撞时间更适合作为风险指标。预警距离类算法常假设车辆减速度为固定值，但实际制动时减速度经常变化［11-12］。文献［11］中基于道路滚动阻力系数提出了一种新的预警距离计算方法，分别考虑前车静止、稳定运动、急减速的情况，对比变加速和传统定加速度方法，结果表明新方法更符合实际情况。文献［12］中改进了避撞标准合作伙伴组织提出的预警策略，设计了新的驾驶员预期响应减速度估计方法，以用于预警距离类模型。该模型可以适用于高风险场景下的预警，降低了仅制动未报警情况的出现次数。上述报警策略可以较好地辅助驾驶员避撞，但模型没有考虑到驾驶员不同风格的影响，不一定适应于不同风格的驾驶员；且系统预警根据的只是当前状态下的危急程度，本文中设计的策略将当前状态和未来预测状态进行综合分析，以做出判断。

驾驶工况会影响驾驶风格。在拥挤的城市，即使冷静型驾驶员也会频繁踩踏板［13-14］。驾驶风格的研究方法主要包括模糊控制［13，15］、无监督学习［16］、有监督学习［17］和贝叶斯理论。文献［18］中对驾驶风格识别常用的特征变量、方法、分类类别和应用进行了综述。文献［19］中为处理手动打标签费时费力的问题，仅利用少量数据聚类结果作为半监督学习的标签，通过S3VM识别驾驶风格。文献［20］中利用半隐马尔科夫模型从驾驶数据中提取出初级驾驶模式，每位驾驶员共有75 种初级驾驶模式，文中通过评估驾驶员间模式分布的相似性，分析驾驶风格。文献［21］中先以车头时距、碰撞时间的倒数为特征进行聚类，从而得到驾驶风格标签，再将相对距离、相对速度、加速度分别进行傅里叶变换和小波变换，对得到的特征变量进行有监督训练，实现驾驶风格分类。

当前文献对驾驶风格的识别也存在两点局限性。一是风格分类器训练采用主观评价或聚类结果做标签，并以准确率作为分类器效果的评价指标。主观评价对于模糊类驾驶员的分类效果不好，不同的评价人员可能得出不同的结论；聚类结果根据数据特征分类，可重复。但驾驶风格是一个主观概念，主观评价结果、聚类结果都不能完全真实。如果模型将基于该种结果的准确率作为评价指标，这会导致结果真实性进一步降低。二是分类是基于小段过程而不是基于人。风格分类主要是为了应用到其他汽车控制系统，以提高驾驶性能。对小段过程进行分类，必须先知道该过程的全部数据，对某一过程来说，这意味着驾驶事件发生是先于分类，则分类无法应用到该段过程。人在一段驾驶过程中表现出的模式，并不一定和相邻时间段一致，这意味着当前段的分类结果也无法应用到其他段。针对上述问题，本文中有如下贡献。

（1）综合两种特征提取方式，用于聚类。将每个驾驶员驾驶数据分为均等的两段，以同一驾驶员不同段变量分类结果是否相同为评价指标。

（2）利用分类结果，优化编码器-解码器模型以实现纵向相对距离预测。

（3）利用预测模型，改进前撞预警系统报警策略，降低误报警次数。

1 数据提取

驾驶数据来源为SPDM（safety pilot model deployment）数据库，数据采集于美国密歇根州安阿伯市，采集频率为10 Hz，本文中选取该数据库中的DAS2 DATASET。DAS2 数据库存储了64 辆车的自然驾驶数据，每辆车都装配有集成安全设备和数据采集系统。雷达采集周围车辆信息，本车的加减速、转向数据由CAN 总线获取。驾驶员日常驾驶不受任何限制，且数据收集处理设备被隐藏，以免对驾驶员行为产生影响。

本文中研究的是跟车工况下的驾驶风格分类，跟车工况主要是纵向运动，因此本文中选取纵向相对距离range、纵向相对速度range_rate、本车加速度ax为研究变量。选取满足跟车工况的数据条件如下：

（1）本车车头与前车车尾距离在4～100 m之间；

（2）跟随同一车辆时长在15 s以上。

根据该条件本文中选取了42 辆车，每辆车的各段跟车时长之和超过3 h。

2 驾驶风格分类

本节中包含下等分位点法和信息熵法两种特征提取方式，二者分别与k-means 聚类方法结合，实现驾驶风格分类，得到下等分位点分类模型和信息熵分类模型。两种模型中，不同段数据分类结果相同的车辆都占多数，效果均较好，但结果仍存在差异，为进一步提高风格分类真实性，以二者交集为最终结果。

2.1 下等分位点分类模型

2.1.1 k-means聚类

首先初始化k个聚类中心，k由人工设定，计算每个点与聚类中心的距离，将每个点分配给最近的聚类中心，再更新每个类的聚类中心，为该类所有点的均值。该过程重复运算直至达到终止条件。

聚类中心初始化采用kmeans++方式。先从数据集中随机选取1 个聚类中心。计算每个点与已有聚类中心的距离d(x)，再由公式p计算每个点被选为下1 个聚类中心的概率，最后采用轮盘法得到下1 个聚类中心。重复上述步骤直至得到全部k个中心。

当前风格分类一般将驾驶员分为3 类［19］或2类［16］，如激进型、一般型、冷静型。本文中也将驾驶员分为3类，即k=3。

2.1.2 特征选择与分类

得到所有车辆的range、range_rate、ax 频数分布数据，如图1所示，分别对3个变量求下分位点，结果如表1和表2所示。

图1 变量频数分布图

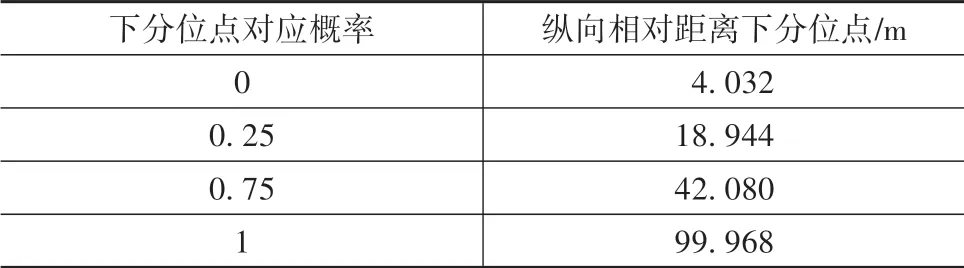
表1 纵向相对距离的下分位点

表2 纵向相对速度及本车加速度的下分位点

纵向相对距离range 的3 个区间分别对应短距离、一般距离、长距离，纵向相对速度range_rate 的5个区间分别对应快速接近、接近、保持、落后、快速落后，本车加速度的5 个区间分别对应急减速、减速、不加速、加速、急加速。在研究1 个驾驶员时，对一段驾驶过程，分别求得纵向相对距离range 在［4.032，18.944）、［18.944，42.080）、［42.080，99.968］3 段中所占时间量trange1j、trange2j和trange3j，然后对应3段区间将各过程的时间量累加，最后3段除以总时间量，完成归一化：式中：trangeij为第j段驾驶过程在第i段相对距离区间中所占时间量；m为区间段个数；n为驾驶过程个数；vrangei为纵向相对距离对应第i段区间的结果变量。

对于range_rate、ax，也采取同样方式获取待聚类变量。车辆10的两部分变量如表3所示。

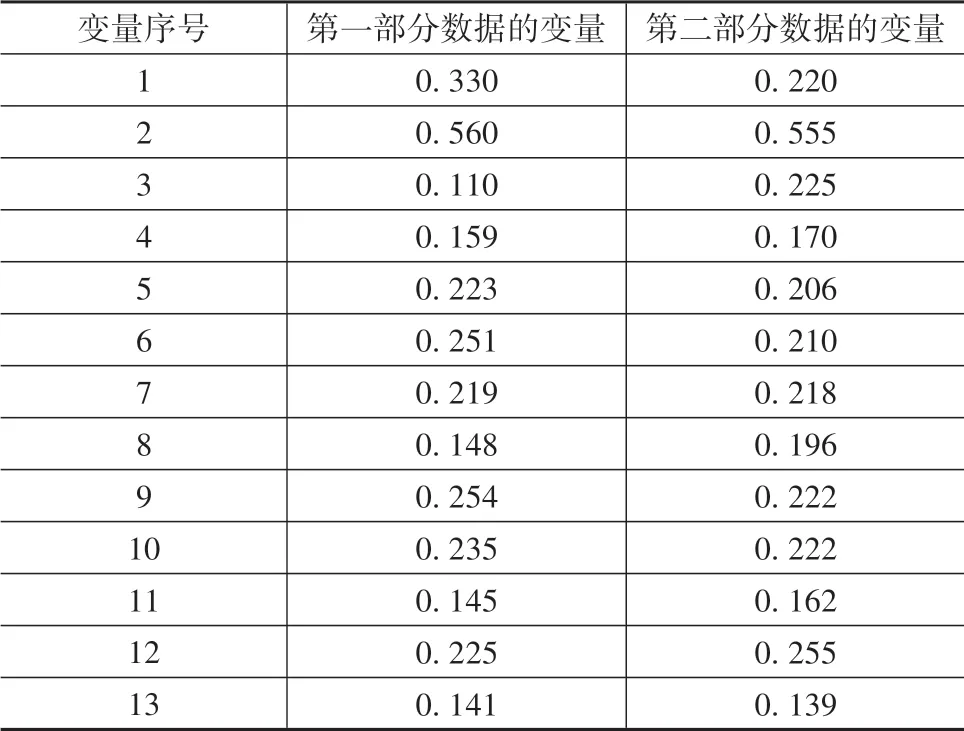
表3 车辆10的两部分变量表

当前向量的维数较高，直接分类会降低分类效果，因而需要先利用主成分分析进行降维，去除数据间的相关性。主成分分析是通过线性变换将高维向量投影到低维空间，同时要确保在低维空间中的投影可以近似表达原向量。模型根据结果向量中主成分的解释率，来确定向量维数，通常来说，主成分累计解释率超过85%即可。结果表明，前3 个主成分累计解释率超过85%，则得到维度为3 的结果向量。再利用2.1.1 节中的k-means 方法聚类，可得到不同驾驶员的风格分类结果。

2.2 信息熵分类模型

2.2.1 信息熵

信息熵是表示样本集合纯度的一种指标。设所有数据分为N类，第k类数据所占比例为pk，则该数据集信息熵计算公式为

entropy值越大，纯度越低，复杂度越高，该数据集所含的信息量越大。文献［16］中正是以高信息熵为准则，得到分隔阈值的。

2.2.2 分隔点的选取

对下等分位点分类模型来说，由于区间分隔点选取根据的是概率等分，range、range_rate、ax 的信息熵不一定最优。信息熵分类模型选取分隔点，根据的原则是使得3 个变量的信息熵尽量大。对range来说，根据驾驶员的所有数据，先将整个区间等分为49份，得到48个分隔点。然后分别尝试去除每个分隔点，计算去除后信息熵，选取剩余信息熵最大的方式去除分隔点。然后以该种方法继续去除分隔点，直到中间分隔点剩余2个，结果如下。

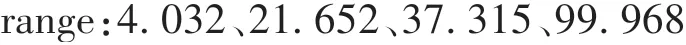
同理，从48 起，减少range_rate、ax 的分隔点数目，保持剩余信息熵尽量大，直到剩余4 个中间分隔点，结果如下。

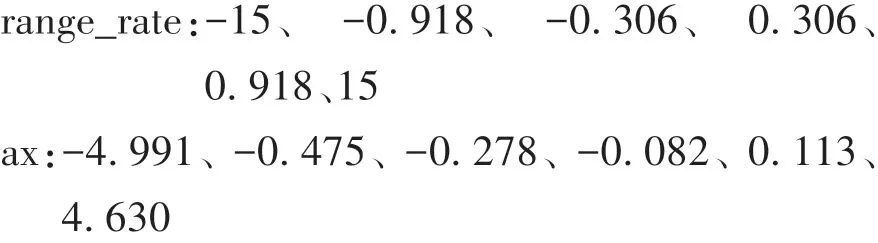
2.2.3 分类

利用2.2.2 节中的分隔点，得到range 变量的3个区间。在研究1个驾驶员时，对应3段区间将各过程时间量累加，再归一化。对于range_rate、ax，也采取同样方式，共得到13 个变量。然后进行PCA 降维，表4描述前3个主成分解释度，总计超过85%，最后利用前3个主成分聚类得到结果。

表4 主成分解释度表

2.3 结果分析

下等分位点分类模型结果中，同一驾驶员不同段变量分类结果相同的车辆数为33，分类结果不同的车辆数为9，表5为具体结果。

对13 个待聚类变量进行直接聚类，可获得具有数学意义的3 个聚类中心。从聚类中心看，一类更冷静，二类处于中等，三类更激进。如聚类中心的前3 个变量分别代表纵向相对距离在［4.032，18.944）、［18.944，42.080）、［42.080，99.968］所占的比例，在第3 个区间中一类占32%，二类占21.7%，三类占14.8%。

信息熵分类模型中，同一驾驶员不同段变量分类结果相同的车辆数为28，分类结果不同的车辆数为14，表6为具体结果。

两种模型中，不同段数据分类结果相同的车辆都占多数，但结果仍存在差异，因此取两种模型分类结果的交集作为纵向相对距离预测的数据集，共25辆车，分类见表7。

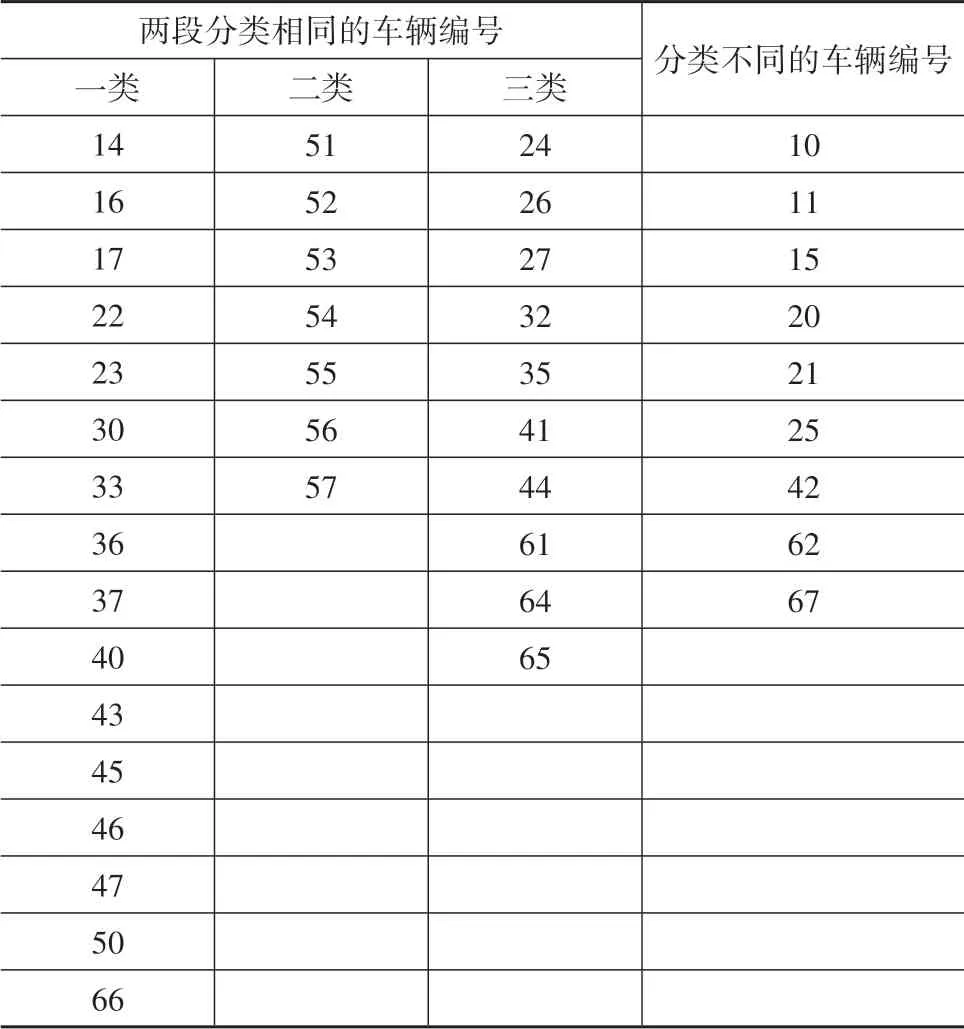
表5 下等分位点分类模型结果

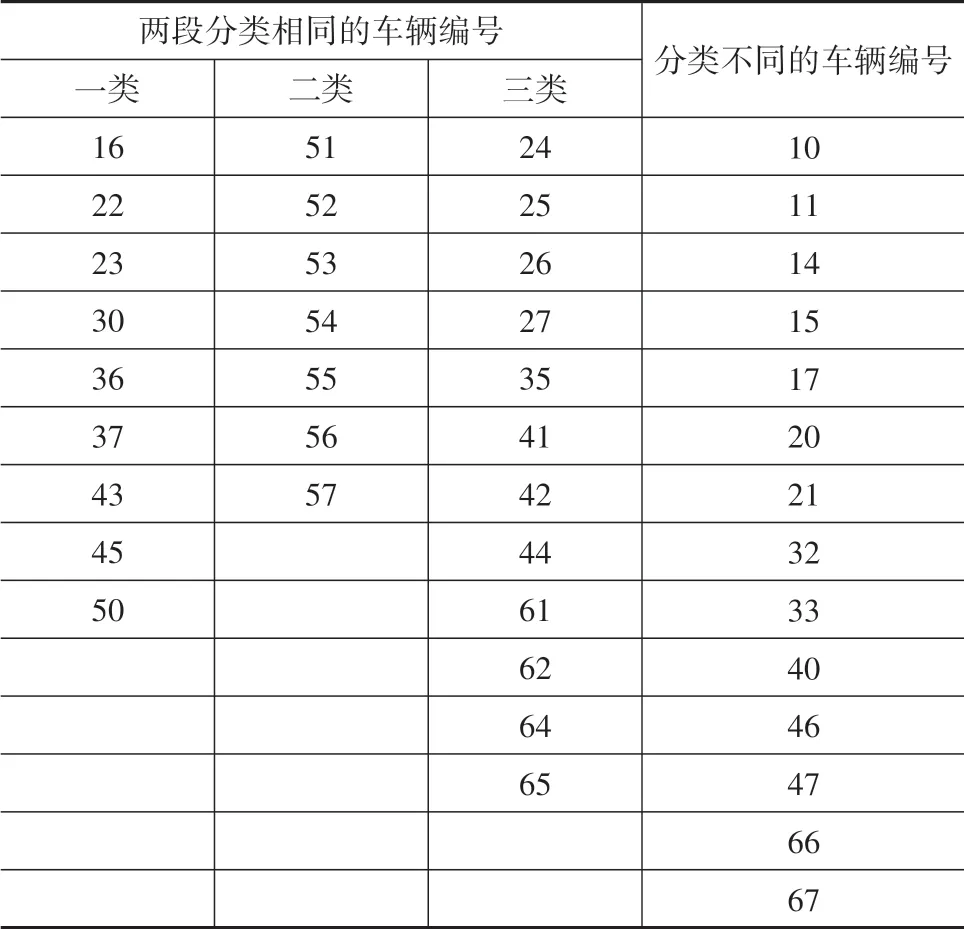
表6 信息熵分类模型结果

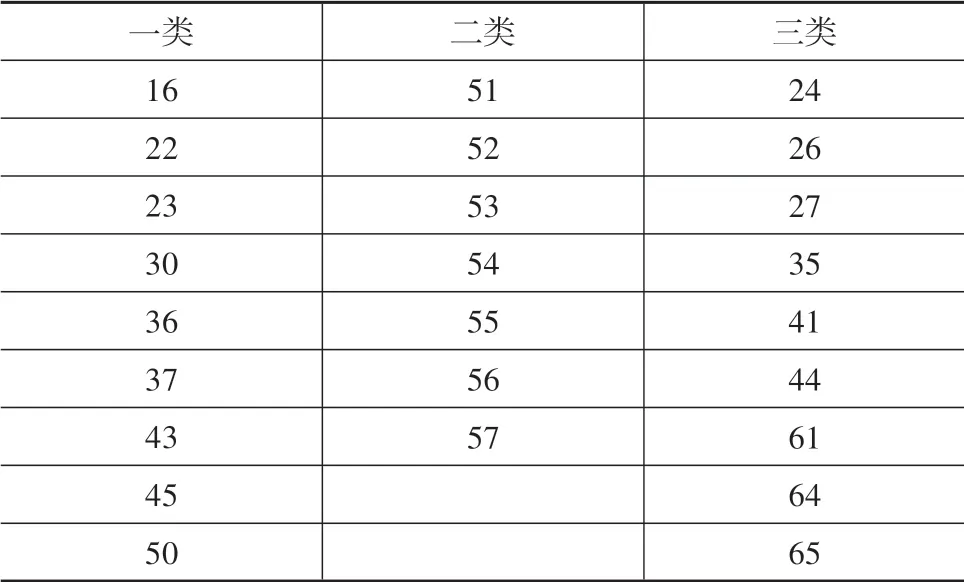
表7 最终分类编号表

3 纵向相对距离预测

3.1 长短期记忆模型（long short⁃term memory，LSTM）模型

LSTM 模型是循环神经网络（recurrent neural network，RNN）的一种［22］，普通循环神经网络存在信息保存时间短、梯度消失的问题，而LSTM 模型可以缓解这些问题。LSTM 模型在循环层单元上不同于普通RNN，其循环层单元包含输入门、输出门、遗忘门3部分，如图2所示，其被称为记忆单元。

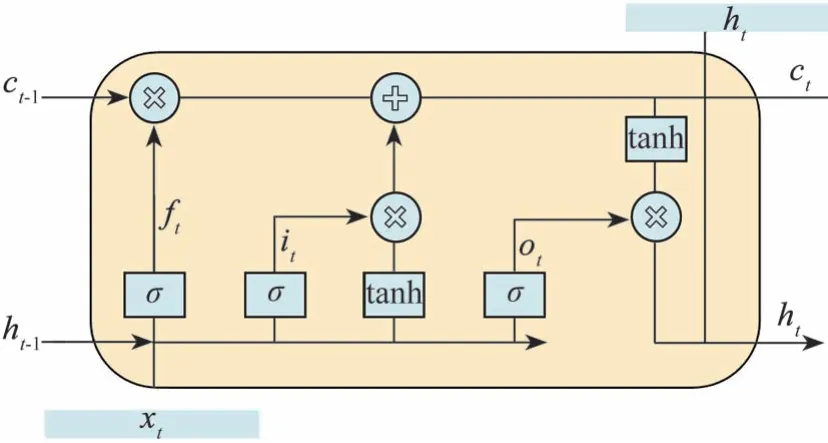
图2 循环层单元示意图

遗忘门决定着记忆单元要丢弃的信息，遗忘门计算公式为

式中：ht-1为上一时刻记忆单元的循环层输出；xt为当前时刻记忆单元的循环层输入；σ为sigmoid函数；Wf为遗忘门权重矩阵；bf为遗忘门偏置矩阵。

输入门决定着存放到记忆单元中的新信息，输入门计算公式为

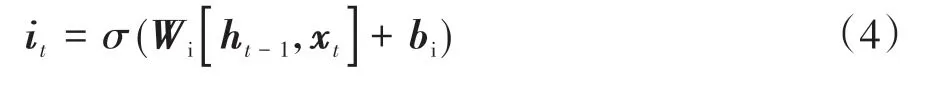
ct-1是包含上一时刻信息的记忆值，其利用输入门计算结果和遗忘门计算结果更新，公式为

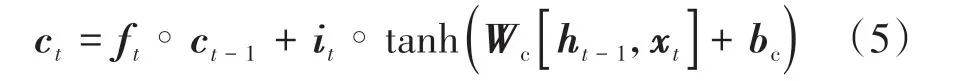
式中：“∘”代表哈达玛积；ct为当前时刻的记忆值。

输出门决定了记忆单元中有多大比例的记忆值可以被输出，计算公式为

循环层输出ht计算公式为

3.2 seq2seq模型

本文中的seq2seq 模型为encoder-decoder，如图3 所示，模型的encoder 部分输入历史数据，模型的decoder 部分输出预测数据。encoder 输入变量为range、range_rate、ax，decoder 的每个单元输入为上一时刻range，输出为当前时刻range 的预测值。变量在输入之前需要经过标准化处理。

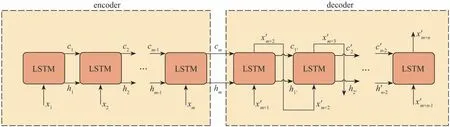
图3 seq2seq模型示意图

seq2seq 模型参数图如图4 所示，FC 代表全连接网络，数字代表网络的神经元数量，decoder 模型输出部分FC-100 层的激活函数为relu 函数。在训练阶段，decoder 所有输入为真实历史数据，代价函数为欧式距离损失函数，使用adam 优化算法。在测试阶段，decoder第1个输入为真实历史数据，其余为前一时刻模型预测结果。由本文中第2部分得到25辆车驾驶数据，以历史时间和预测时间之和为一段过程的时长，将每辆车的数据进行分割，最后将分割好的数据按4∶1分配，得到训练集和测试集。

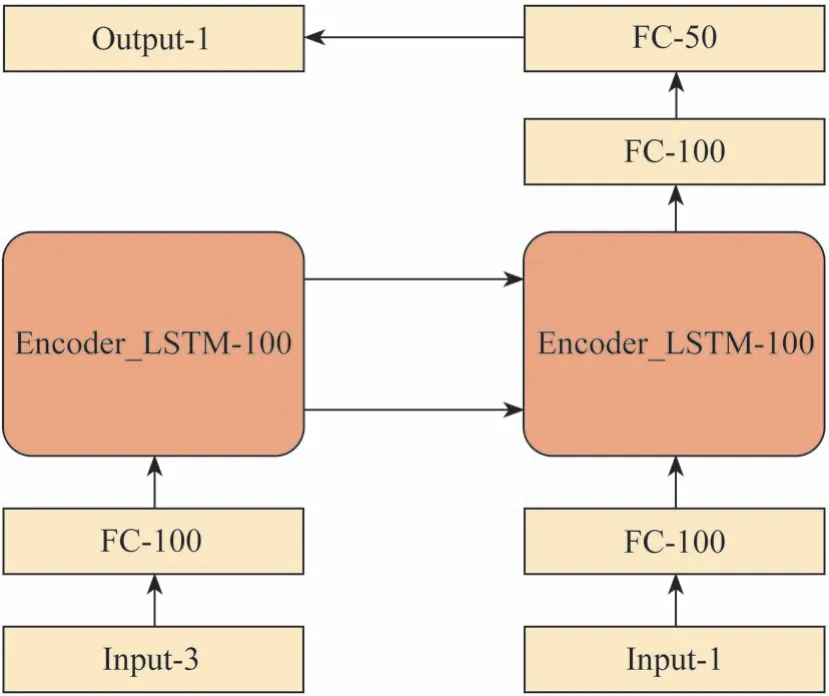
图4 seq2seq模型参数图

3.3 个性化seq2seq模型

文中第2部分得到风格分类较真实的25辆车数据，共分为3 类。本小节中将根据3 类数据和3.2 节中训练后模型参数创建3 类个性化seq2seq 模型，结构如图5 所示，为提高模型对每类数据的学习能力，在个性化部分增加1 个全连接层。每类个性化seq2seq 模型中encoder、decoder 输入部分和LSTM 部分共用3.2 节中训练后模型参数，然后使用每类对应的驾驶数据训练模型剩余部分，这通过设置学习率来实现，共用部分学习率设置为10-5，以限制共用部分参数改变，个性化部分学习率设置为10-3。

图5 个性化seq2seq模型参数图

3.4 结果分析

预测模型评价指标选取为均方根误差，设M为样本量，则预测时间内误差计算公式为

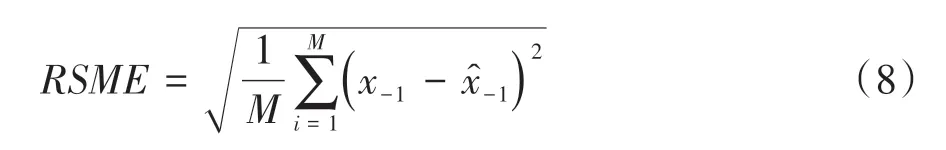
式中：x-1为预测过程中最后一个时间点的真实值；为预测过程中最后一个时间点的预测值。

图6 为训练过程中代价误差的变化图。代价误差是标准化后纵向相对距离预测值和真实值之间的误差，量纲为1。误差描述了模型预测纵向相对距离效果的好坏。误差越小，则说明预测性能越好。本文中的一批数据量大小为100，模型利用每批数据计算得到代价误差，然后进行反向传播以更新参数。从图6 可以看出，随着模型参数更新，各批数据的代价误差不断降低，训练效果越来越好。

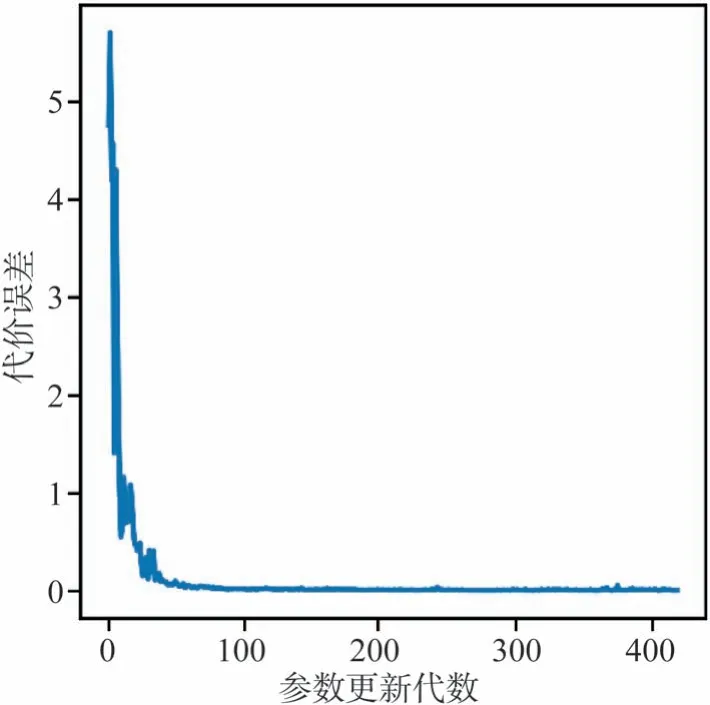
图6 seq2seq模型代价误差更新图

表8 描述了模型优化前后测试评价指标的变化，试验分别进行了两组训练测试，一组为3.6 s 历史数据输入、1.2 s 预测数据输出，另一组为6 s 历史数据输入、2 s预测数据输出。从表8可知，优化后模型的结果误差有一定降低。

表8 个性化优化前后模型测试结果误差

4 前撞预警策略的改进

4.1 前撞预警策略

预警距离经常被预警策略作为特征量，其计算的方式有许多。一种常用的方法就是计算从驾驶员反应过来需要制动到本车车速降低至和前车相同、且两车不相撞所需的最小纵向相对距离［4，23-24］。本节中策略正是利用这种方法且假设条件为前车车速不变，本车以最大减速度减速。这种预警距离计算方法适用于弧度较小的道路。本节中前撞预警策略基于Euro NCAP AEB Test Protocol，包含3种状态，具体规则如下。

（1）安全

最重要被检测对象（本车航道上位于前方且距离最近的对象）正在远离本车或者与本车的距离为常量。

（2）注意

最重要被检测对象正接近本车，但纵向相对距离仍大于FCW 报警距离。FCW 报警距离随纵向相对速度变化，接近速度越高则该距离越大。

（3）报警

最重要被检测对象正接近本车，且纵向相对距离小于FCW报警距离。

由Euro NCAP AEB Test Protocol 确定 的FCW 报警距离计算公式为

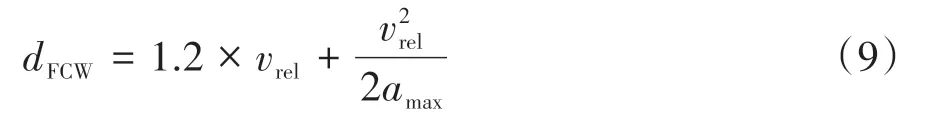
式中：dFCW为FCW 报警距离；vrel为前后车纵向相对速度的绝对值；amax为最大减速度，其被设为0.4 倍重力加速度［23］。

本文中使用数据库为自然驾驶数据，驾驶过程为人工操作，无辅助系统，且无事故发生。将上述前撞预警策略应用于本文中第3 部分车辆数据，25 辆车共发生253 次报警，其中误报警次数为123 次（在不发生事故的前提下，前撞预警系统报警但驾驶员判断无需制动，则此时的报警为误报警），如图7 所示。原因应该是该策略仅判断当前时刻的危急性，没有将当前状态和未来预测状态综合考虑，且没有考虑驾驶员不同风格的影响。

图7 基于4.1节中预警策略的各个车辆误报警次数

4.2 改进后策略

为降低误报警次数，本文中利用第3 部分个性化预测模型和4.1 节中报警策略，设计新策略，条件如下：

（1）当前时刻及预测时刻均满足4.1 节中报警策略；

（2）连续0.5 s满足（1）条件。

本文中纵向相对距离、纵向相对速度均采用第3 部分预测模型。图8 描述了在一段行驶过程中车辆16 纵向相对距离真实值和预测值的变化情况。图8（a）预测模型的输入时长为3.6 s，输出时长为1.2 s。图8（b）预测模型的输入时长为6 s，输出时长为2 s。从第3 部分结果和图8 分析可知，预测时长越短，预测精度越高。这是因为当前时刻预测结果是以前一时刻预测结果为输入，而前一时刻预测结果本身就存在误差，这使得误差不断积累，在最后一个预测时刻表现出更大的误差，因此本文中预测时长选择1.2 s。

历史时长分别选择2.4和3.6 s，对比两组结果。前者误报警次数为78，后者误报警次数为50，后者的各个车辆已减少误报警次数如图9 所示。历史时长3.6 s 比历史时长2.4 s 的误报警次数低，原因应该是更长的历史时长包含更多的时序信息，有助于预测精度的提高。改进后策略可降低误报警次数，且历史时长3.6 s、预测时长1.2 s 的报警策略模型误报警次数更低。如果需要进一步降低误报警次数，可能需要提高模型在更长时间预测时的精度。

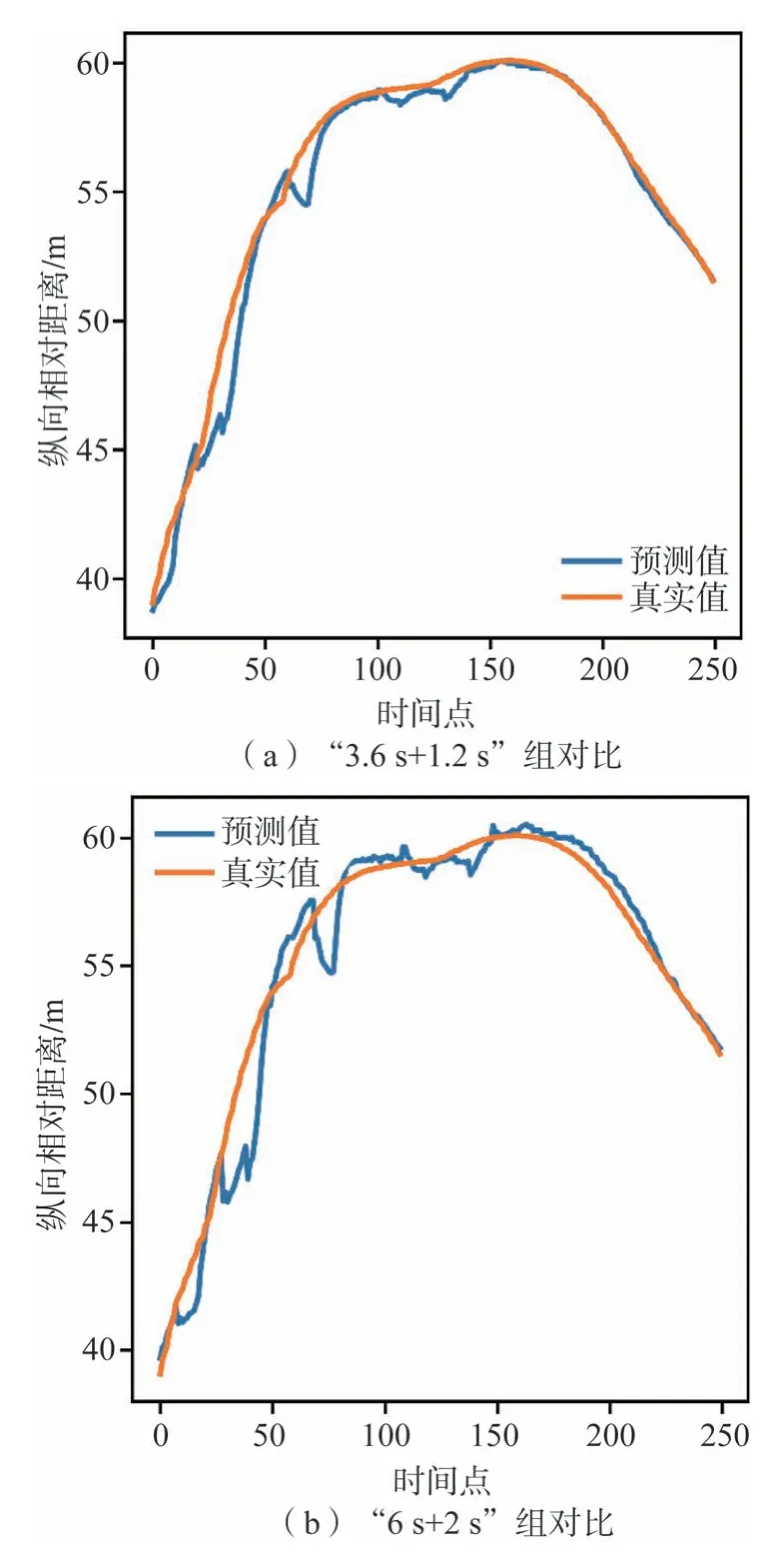
图8 车辆16第一段驾驶过程数据的纵向相对距离预测与真实结果对比

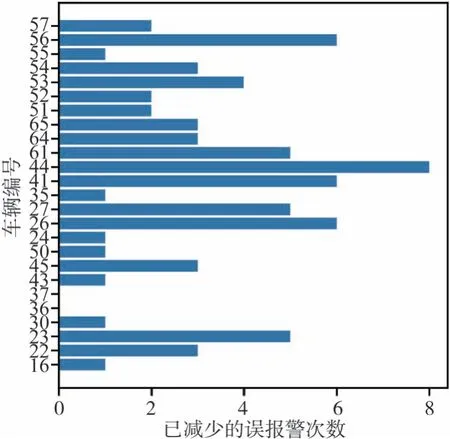
图9 基于改进后预警策略的各个车辆已减少误报警次数

5 结论

本文中设计了一种基于驾驶风格的纵向相对距离预测模型，并利用该模型改进了前撞预警策略。驾驶风格分类模型结合了两种特征提取方法，即下分位点法、信息熵法，使用k-means方法聚类，以车辆两部分数据分类结果是否相同为评价指标。两种模型中分类结果相同的车辆数与不同的车辆数之比分别为33∶9 和28∶14。综合两种模型，以二者交集为最终结果。纵向相对距离预测模型采用基于LSTM的编码器-解码器框架，以风格分类结果全部数据训练可得到预测模型的共用部分参数，个性化部分分别利用3 种驾驶风格对应数据集训练得到。文中对比了个性化优化前后模型在“3.6 s+1.2 s”和“6 s+2 s”两组预测中的结果，结果表明驾驶风格优化后的模型有更低的预测误差。本文中将预测模型应用到前撞预警策略中，输入的历史数据时长为3.6 s，输出的预测时长为1.2 s，误报警次数由原来的123降低至50，减少至原来的40.65%。如果需要根据新驾驶员特性改善预警性能，先要利用该驾驶员的特征变量对比已有模型的3 个聚类中心，以最近的聚类中心类别为新驾驶员类别，再根据类别选择已有的纵向相对距离预测模型。最后利用新驾驶员的预测模型，实现本文中上述说明的改进后预警，降低误报警次数，提高新驾驶员对前撞预警系统的接受程度。