基于群组DEMATEL与灰关联投影的供应商质量绩效评价
2021-04-13何杜博石文成
何杜博, 黄 栋,*, 石文成
(1.海军工程大学管理工程与装备经济系, 湖北 武汉 430033; 2.陆军勤务学院军事物流系, 重庆 401331)
0 引 言
目前,由于装备采购业务中外包外协产品所占比例逐渐增多,供应主体日益多元化,装备采购供应链中隐含的各种质量风险越来越多。建立科学有效的装备采购供应链环境下的供应商准入评价体系和评价方法,是装备采购供应链质量保证体系构建和运行的核心要务。而系统性的评价装备采购供应商质量绩效,对于供应链潜在质量问题识别、运作结构优化、运行效率提高都具有重要意义。
质量绩效是组织在其质量经营活动过程中,用来表现其产品质量、运行质量和经营结果特性的特征量,是指组织通过自身和外部的质量管理所创造的卓越绩效。供应商质量绩效具有多维度性和复杂性,其衡量的不仅是供应商自身质量行为的绩效,还包括其在供应链质量管理上维持的绩效水平。装备采购部门往往会寻求不同背景的评价专家组成决策小组进行供应商考核,通过集结群决策信息,得到可信度较高的主观评价信息,并结合实际收集的客观数据信息来对供应商进行综合评估[1]。实际评价中,部分质量绩效指标信息存在一定的模糊性。
因此,装备采购供应商质量绩效的评价是一类模糊混合型多属性群决策问题。现有的模糊多属性群决策方法主要是通过选取能有效描述决策者主观评价信息的数据类型,如直觉模糊集[2-5]、概率语义术语集[6-7]、二元语义[8-10]等。利用主客观赋权的方法如层次分析法[11-12]、数据包络分析[13-14]、熵权理论[15]确定指标权重,最后基于多属性决策方法或集结算子如基于理想解方法[16-18]、直觉模糊集结算子[19-21]等来综合评价信息,得到评估对象最终的优劣排序。
上述方法虽然能得到较为客观的结果,但在评价装备采购供应商质量绩效中仍存在以下不足:① 评价方法中只考虑了决策者的单一主观评价数据类型,未将实际评价中可以得到的客观指标数据纳入评价范围;② 群决策信息集结过程中尚未考虑不同决策者之间主观判断及事物模糊偏好信息的关联性,使得集结后的评价结果不贴近实际;③ 以上方法鲜有考虑评价指标之间的内在关联,导致某些评价指标的赋权容易造成偏差。
为此,本文提出一种基于决策实验室分析法(decision making trial and evaluation laboratory,DEMATEL)与灰关联投影的混合多属性群决策模型。该模型考虑了供应商质量绩效评价中客观性统计数据和主观性判断融合的情形。利用模糊测度来描述群决策中不同专家联盟之间的内在关联性,引入广义λ-Shapley Choquet算子来集结群决策主观评价信息。然后,将DEMATEL拓展到群体模糊决策领域,用以确定评价指标的权重,使得权重确定过程中更能考虑指标间的关联性。最后,利用混合灰关联投影法对不同对象进行客观评价,规避数据类型转换带来的损失,提高评价的准确性和客观性。
1 装备采购供应商质量绩效评价体系
在装备采购供应链构建初期,军方与总承包商签订武器装备采购合同,确定了武器装备采购的初步计划。作为供应链核心的总承包商会通过招标采购的方式搜寻潜在的合作承制单位,重点对承制单位资质、质量管理体系和产品认证、企业单位各方面绩效进行考察,将具有合作资格的承制单位纳入装备采购承制单位目录(供应商库)中。装备产品服役年限长、质量要求高、产品需求多变等特点决定了其在供应商的选择上与一般民用产品供应商选择存在较大差别。从装备采购供应商的内外部质量绩效考虑,有以下4个评价维度。
(1)装备采购供应商应当具有良好的质量控制能力。质量是装备配套产品最基本的要求,其要求供应商具有良好的质量保证能力,使得产品的制造过程质量得到保障。
(2)装备产品的研制生产中存在大量的技术创新,因此其供应商应当具有良好的技术支撑能力,以便产品换代升级时能够快速适应供应需求,满足军方各项技术指标要求。
(3)装备产品服役时间较长,在产品寿命周期内其供应商应当具有良好的服务协同能力,在售前和售后都能快速响应军方客户需求,并通过及时调整生产计划来满足需求。
(4)供应商的产品交付能力是考核供应商的基本准则之一,其决定了装备产品的研制生产进度。同时,供应商还应当具有一定的提前交付能力,以应对紧急情况下的各项交付需求。
建立的指标体系如表1所示。
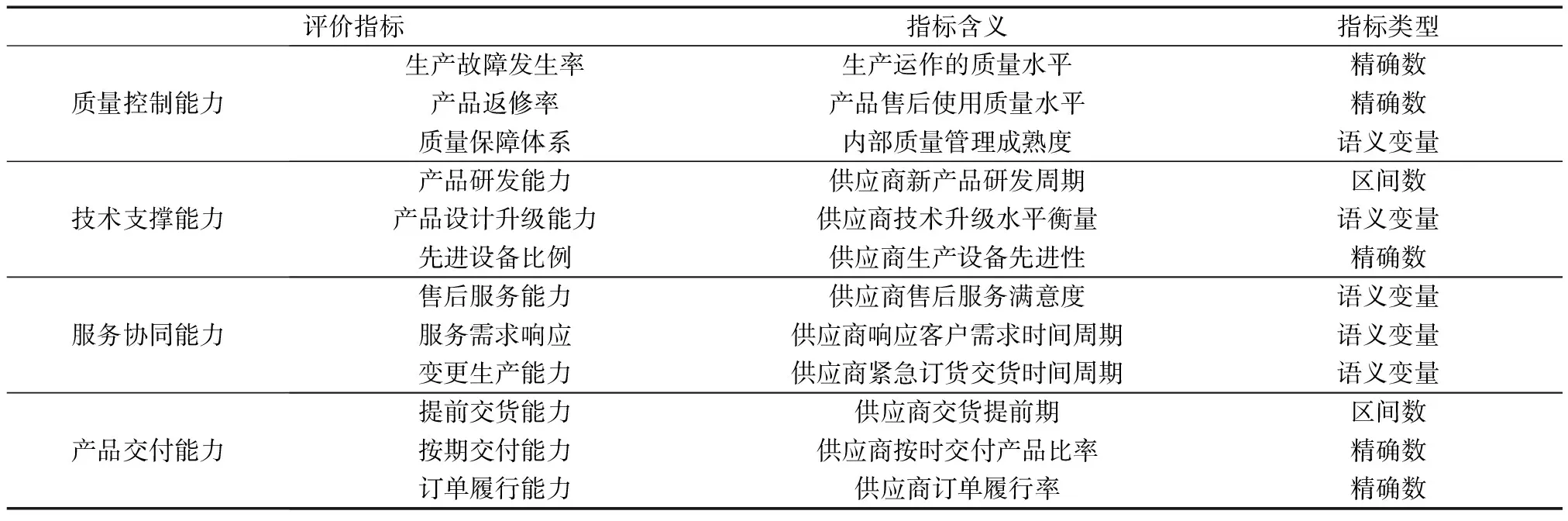
表1 基于供应链的装备采购供应商质量绩效评价体系
2 理论基础
考虑供应商质量绩效评价中涉及不同评价准则、客观的统计数据和主观的判断信息等。为了简化研究问题,将客观数据类型(如精确数、区间数)统一为区间数类型(如精确数a可以转化为区间数[a,a]);而主观判断信息主要是由专家通过语义变量或模糊数形式给出,具有一定模糊性和犹豫性。直觉模糊集通过隶属度、非隶属度和犹豫度来描述决策者的评价信息,能更加细腻地刻画出人们对客观事物的判断。不同专家的评价准则粒度不同,利用转换公式将其统一转化为直觉模糊数,提高计算效率。
2.1 区间型数据相关定义
定义 1[22]任意给定两个区间数a=[aL,aU],b=[bL,bU],a与b的距离为
(1)
2.2 直觉模糊数相关定义
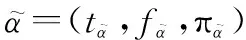

(2)
2.3 语义变量与直觉模糊数的数据转换
语义变量是指以自然语言短语的形式来评价某个对象的模糊属性,决策者一般通过选取熟悉合适的语义变量来表达其给出的主观判断信息。为数据处理方便,将语义变量统一转换为直觉模糊数,以便更好地处理主观判断信息。给出语义变量转换到直觉模糊数的统一定义如下。
定义 3[24]设任一语言评价集
q个语言评价粒度对应的直觉模糊数形式表示为
(3)
(4)

2.4 模糊测度和Choquet积分算子
定义 4[25]设S为一有限集合,P(S)表示S的幂集,若μ:P(S)→[0,1],若满足下列条件,则称μ为定义在(S,P(S))上的模糊测度。
(1)μ(∅)=0,μ(S)=1;
(2)A,B∈P(S),A⊆B⟹μ(A)≤μ(B)。
定义 5[25]假设对于任意的C,D∈P(S),C∩D=∅,有
γλ(C∪D)=γλ(C)+γλ(D)+λγλ(C)γλ(D)
式中,λ∈(-1,+∞),称γ为λ的模糊测度,记为γλ。
对于有限集S,γλ满足下列条件:
(5)
易知μ(S)=1,λ可以通过
(6)
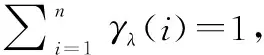
定义 6[26]若f为定义在S上的非负函数,μ为定义在S上的模糊测度,则f关于模糊测度μ的离散Choquet积分为
Cμ(f(x(1)),f(x(2)),…,f(x(n))=
(7)
式中,(i)表示f(x(i))一个置换,0≤f(x(1))≤…≤f(x(n));A(i)=(x(i),x(i+1),…,x(n));A(n+1)=0。
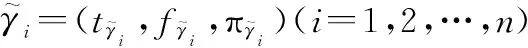
(8)
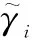
2.5 广义λ-Shapley Choquet积分算子
考虑主观评价中专家联盟(集合)决策中存在的内在关联,传统加权平均法来集结主观判断信息会使评价结果产生偏差。模糊测度以约束条件较弱的单调性和连续性取代经典概率中的可加性约束,能很好地描述不同指标或专家主观评价之间的相互关联[28]。因此,通过模糊测度确定关联条件下各专家联盟权重,并利用Choquet积分集结各位专家对主观绩效指标的模糊判断,以确定各主观绩效指标的综合评价值。但从离散Choquet积分定义可知,其只对相邻因素的相互影响关系进行了分析,只考虑了专家联盟中的一种情况。但实际情况中,不同因素之间的关系是随机的,所有因素之间的相互关系是未知的,这就要求模糊测度应当是每个因素或不同因素构成集合的模糊测度的平均值。为更好地解决此问题,根据文献[27]的思路,引入Shapley函数到模糊测度与Choquet积分算子中。利用Shapley函数在合作博弈中通过单个局中人在群决策中所做贡献来确定局中人利益的特征,其分配利益方式可以很好地应用到群决策的权重确定中。广义Shapley函数[29]值为
(9)
特别地,当X={xi}时,令|X|=x,根据式(5)和式(9)有
(10)
式中,γλ为S上的模糊测度,式(10)反映的是每个专家、专家联盟之间的整体平均模糊测度,其整体考虑了所有专家构成的不同集合之间的模糊测度,更贴近实际。
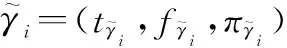
(11)
易证明其幂等性、有序单调性、有界性和置换不变性等性质。通过AIFGSC可以有效集结具有模糊测度的主观决策信息。
2.6 专家模糊测度计算

考虑以上两方面因素来确定每个专家的模糊测度,引入直觉模糊数的Hamming距离函数和直觉模糊熵。通过求解不同专家给出的决策矩阵之间的距离测度来确定专家的模糊测度。
(12)
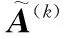
(13)
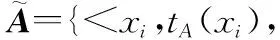
(14)
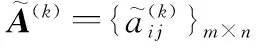
(15)
根据式(13)和式(15)专家ek的λ模糊测度可被定义为
(16)
显然γλ(ek)∈[0,1],此定义方法得到的λ模糊测度具有较好的特性。专家给出的决策矩阵模糊熵越小、与群体决策信息偏离程度越小,其能够为决策提供的信息更多,其模糊测度越大。此定义能减少单个专家评价与整体评价偏差较大带来的不良影响,同时考虑专家评价中的信息量。在求得所有专家的λ模糊测度的基础上,通过式(5)和式(6)可以得到λ值及不同专家联盟(集合)的模糊测度。
在求得所有专家联盟(集合)和个体的模糊测度值后利用AIFGSC集结群体决策信息,得到考虑了所有专家个体和专家集合之间的关联性的各个主观性评价指标的综合评价信息,其形式仍是直觉模糊数,避免了因数据转换而造成的评价信息的损失。
2.7 基于AIFGSC的群组DEMATEL属性权重确定
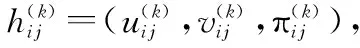
(17)
同理,根据专家群体在对主观属性指标进行评价过程中所确定的模糊测度γλ(ek),通过AIFGSC来集结专家判断矩阵,从而得到最终的综合判断矩阵
H=[hi j]s×s=
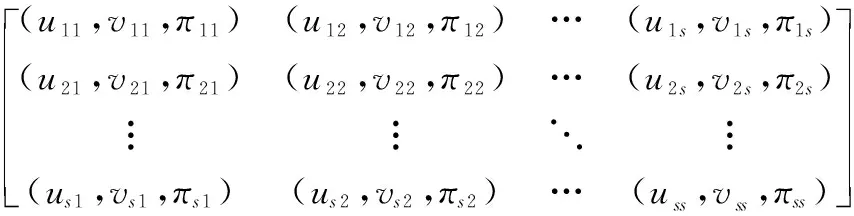
(18)
式中,hi j=(ui j,vi j,πi j)为AIFGSC集结各个专家判断矩阵信息后所得的判断信息。引入风险偏好系数τ来将综合判断矩阵去模糊化,得到实数化矩阵B=[bi j]s×s,其中bi j为去模糊化后的群体决策确定偏好度,其计算公式为
bi j=ui j-vi j+(2τ-1)πi j
(19)
式中,τ∈[0,1],τ>0.5则表示群决策是风险偏好的;τ≤0.5则表示群决策是风险规避的。对确定信息的群体判断矩阵B=[bi j]s×s进行标准化:
(20)
得到标准化矩阵T=[ti j]s×s。确定综合影响矩阵R:
(21)
根据R可以确定各个属性的影响度Pi,被影响度Qi,中心度Mi及原因度Xi:
(22)
(23)
Mi=Pi+Qi
(24)
Xi=Pi-Qi
(25)
则最终的属性权重可以由Mi和Xi的几何平均数确定:
(26)
(27)
可以得到最终的属性权重向量ω=(ω1,ω2,…,ωs)。
3 改进的灰关联投影法
灰关联投影法通过结合灰色系统理论和矢量投影原理来进行多属性决策,其优势在于能在指标空间中较为全面地分析属性之间的相互关联,避免了单方向偏差,能在复杂的系统决策中发挥较好的效用。为了更好地处理混合型数据信息,将传统灰关联投影法进行扩展。
3.1 建立方案集评价矩阵
由于指标属性形式不同,为了保证在指标空间中各指标之间的等效性和同序性,首先对不同形式的原始数据进行规范化处理,消除量纲不同带来了影响。设有备选方案集X={X1,X2,…,Xm},指标集R={Rj|j∈I1,I2},其中:I1为区间数型评价指标集,I2为直觉模糊数型评价指标集,分别对I1和I2形式的原始数据进行规范化处理。
(1)I1型数据
(28)
(29)
(2)I2型数据
(30)
式中,B为效益型指标;C为成本型指标。于是,备选方案集X对于指标集R的规范化评价矩阵为
X=(ui j)m×n,i=1,2,…,m;j=1,2,…,n
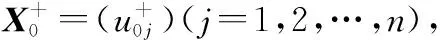
(31)
(32)
3.2 加权灰关联决策矩阵建立
记Δi j为理想方案向量X0与备选方案向量Xi在属性Rj上的绝对差值,即
Δi j=|u0j-ui j|=
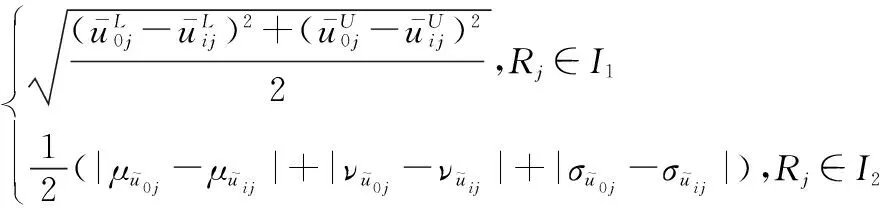
(33)
由灰色关联理论可知,每个属性值ui j对理想方案向量X0的灰关联系数为
(34)
式中,α为分辨系数,α∈[0,1],通常取α=0.5。
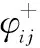
(35)
(36)
记权重向量为ω=(ω1,ω2,…,ωn),对矩阵G+和G-分别加权可以得到加权正负灰关联决策矩阵分别为
(37)
(38)
3.3 计算灰关联投影值
由于每个备选方案都是灰关联决策矩阵中的一个行向量(矢量),则每个备选方案向量Xi与理想方案向量X0之间的夹角θi为灰关联投影角,其余弦值为
(39)
记备选方案向量Xi的模为ai,则备选方案向量Xi在理想方案向量X0上的投影值为
(40)
式中,
(41)
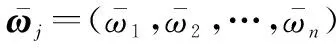
(42)
(43)
根据文献[30-33],定义灰关联投影系数Ei综合衡量方案Xi靠近优势方案和劣势方案的程度。
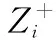
(44)
综上所述,本文模型的具体步骤如下。
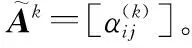
步骤 2通过第2.6节中提出的专家模糊测度公式,确定每个专家ek的λ模糊测度及专家决策集合E={e1,e2,…,eq}不同子集(专家联盟)的λ模糊测度,并通过第2.5节所提公式确定不同子集的广义λ-Shapley指标值。
步骤 3利用AIFGSC集结专家评估信息,得到直觉模糊数形式的综合主观评价信息。
步骤 4邀请原专家群体对评价指标集中各个指标间的影响关系进行二次评价,得到个体模糊决策矩阵,并根据计算所得的专家模糊测度,通过AIFGSC集结后得到综合模糊决策矩阵。并根据第2.7节中的方法确定属性权重。
步骤 5利用第3节中的多属性决策方法,计算灰关联决策矩阵,并将属性权重代入计算正负加权灰关联矩阵。求出不同方案的灰关联投影系数,并根据灰关联投影系数来对不同备选方案进行排序择优。
模型的具体框图如图1所示。
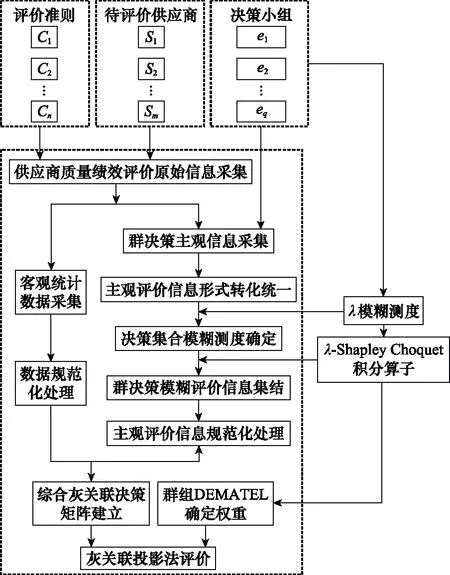
图1 供应商质量绩效评价步骤
4 算例分析
4.1 备选供应商择优排序
以某型号装备采购供应商准入评价为例,为了从资质合格名单中对质量绩效良好的供应商进行再次筛选评价,确定4个备选供应商S={S1,S2,S3,S4},分别由来自装备论证、装备研制和装备采购部门的决策者E={e1,e2,e3}组成决策小组对备选供应商进行择优评价。其质量绩效评价准则如表2所示,其中B为效益型指标,C为成本型指标。采集到的原始信息如表3~表6所示,其中包括专家群体{e1,e2,e3}对4个供应商的主观属性准则的评估矩阵。语义变量类型准则的评价已转换为直觉模糊数,客观属性的评价准则通过实际考察数据统计得到。
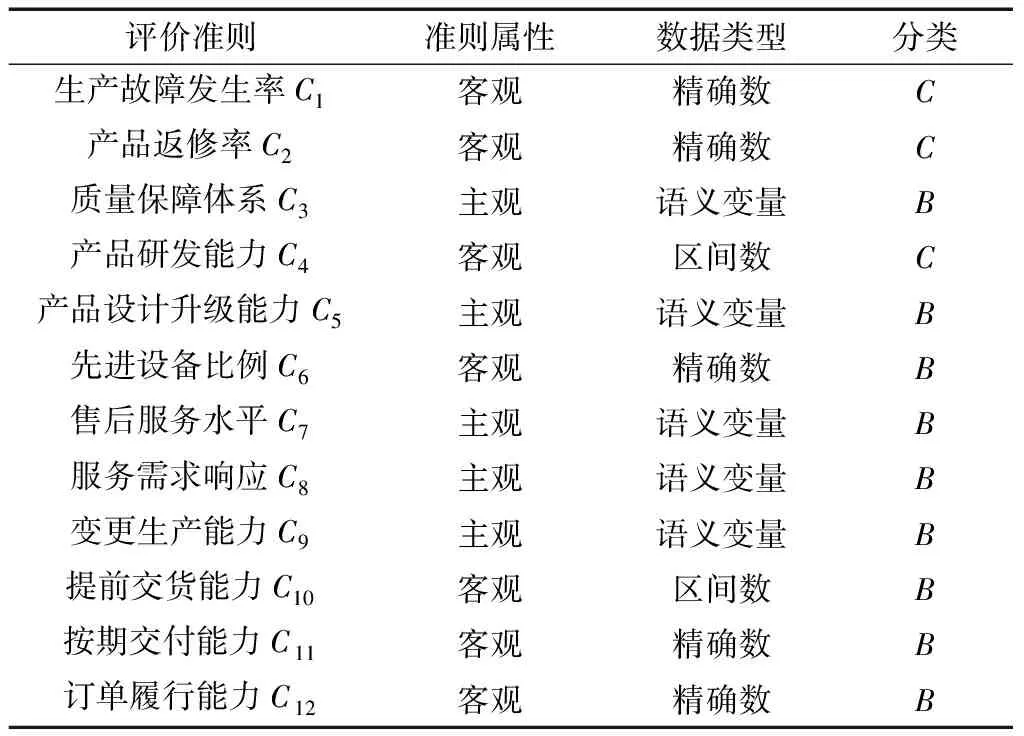
表2 装备采购供应商质量绩效评价准则
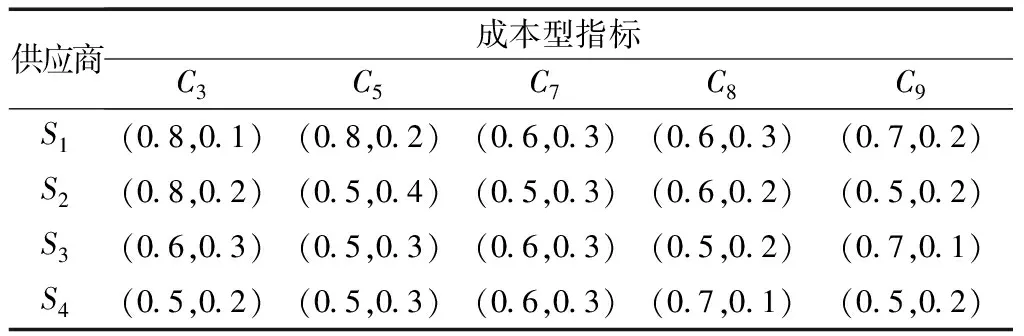
表3 专家e1的主观决策矩阵
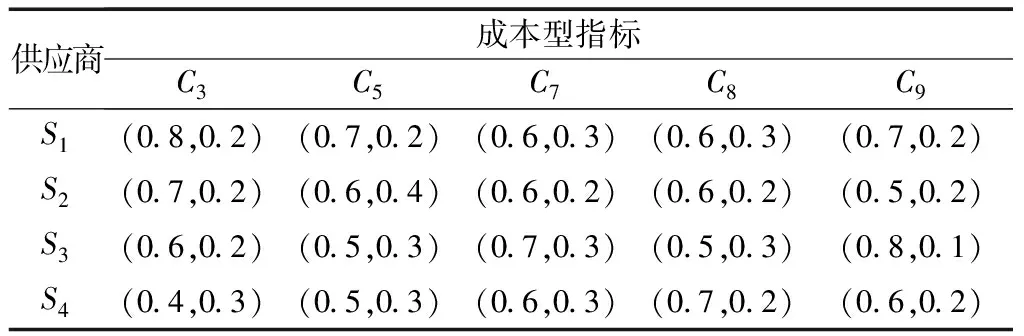
表4 专家e2的主观决策矩阵
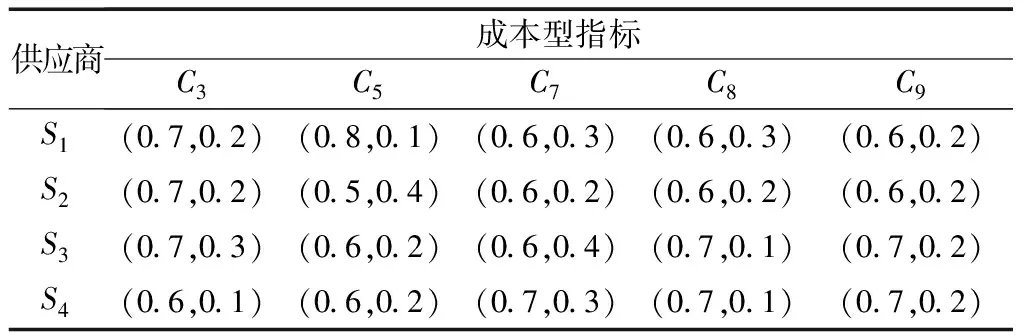
表5 专家e3的主观决策矩阵
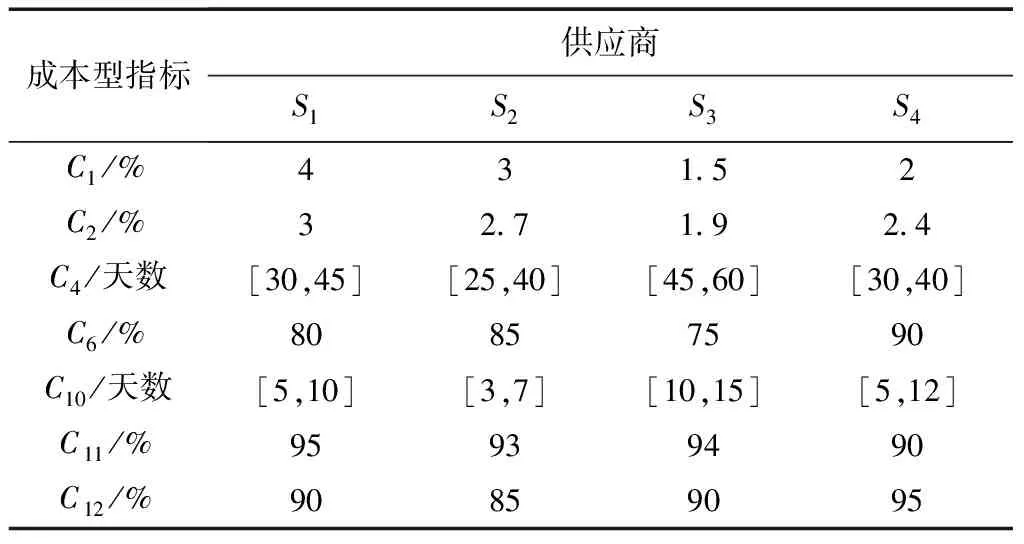
表6 供应商客观属性准则评价值
步骤 1根据式(11)~式(16)可以得到专家个体的模糊测度,将其代入式(5)和式(6)求出不同专家联盟的模糊测度,得到λ-Shapley模糊测度如表7所示。
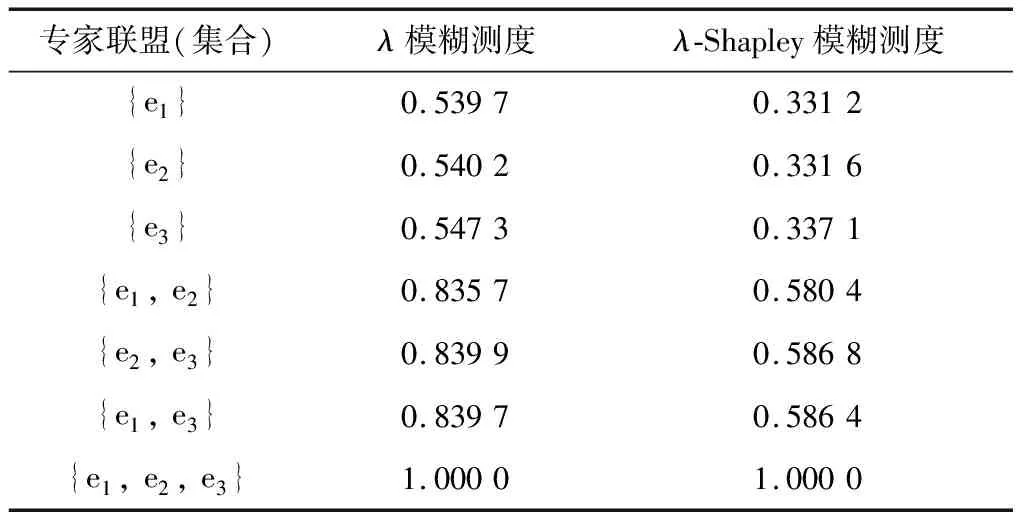
表7 专家联盟的λ模糊测度及λ-Shapley模糊测度
根据不同专家联盟的λ-Shapley模糊测度,利用AIFGSC集结专家信息,得到最终主观综合评价信息如表8所示。
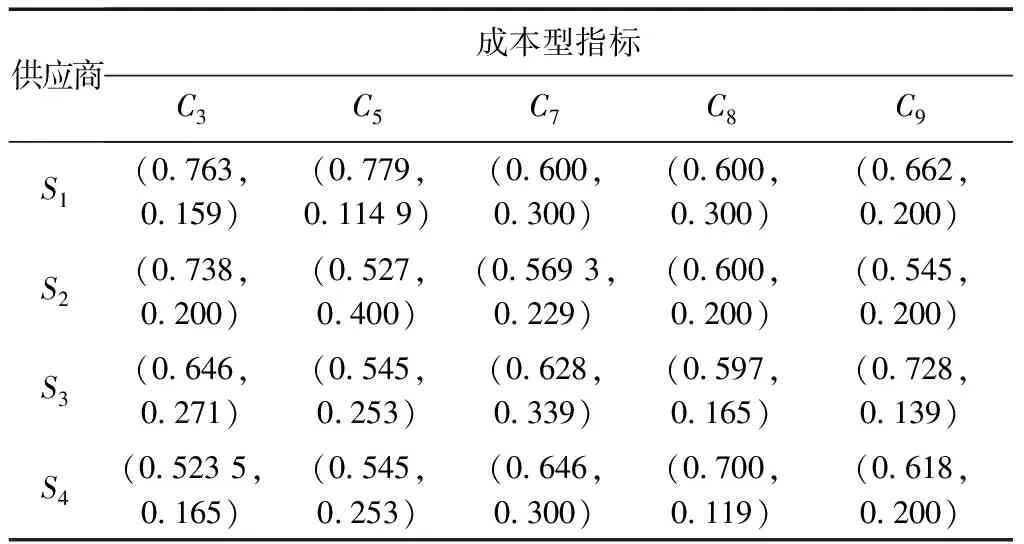
表8 专家综合主观决策矩阵
步骤 2邀请原专家群体{e1,e2,e3}对指标之间的影响度进行评价,利用其在指标评价阶段所计算得到的模糊测度,通过AIFGSC集结专家评价矩阵,基于第2.7节中DEMATEL来确定指标权重,各个指标的中心度与原因度分布如表9所示。
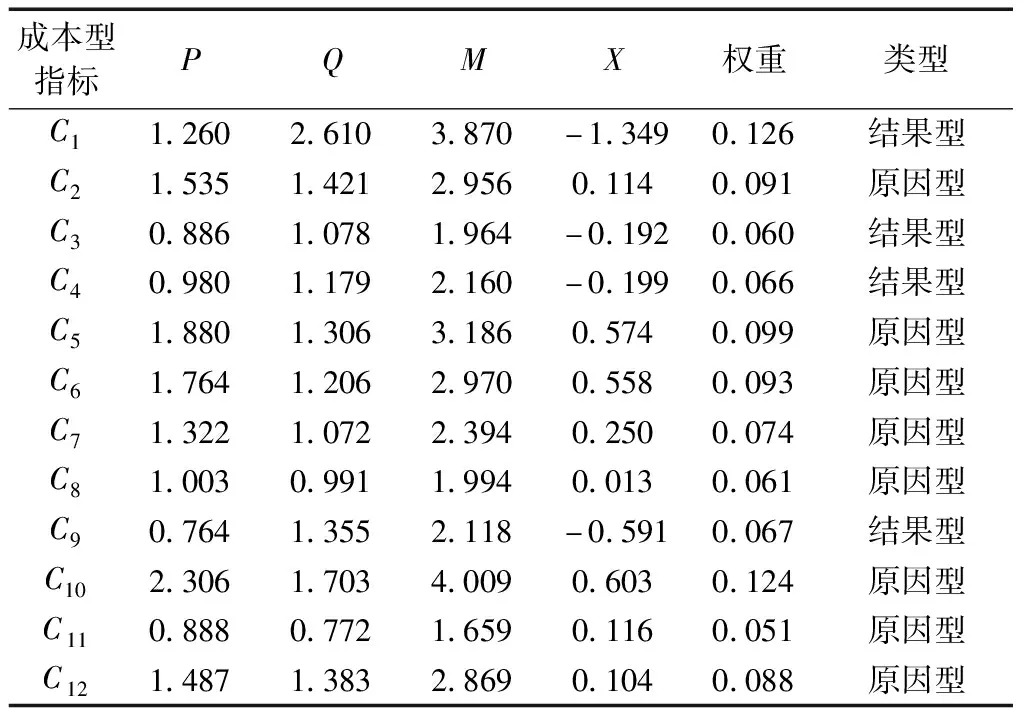
表9 各个指标影响度分析及类型确定
根据各个指标中心度与原因度确定指标权重向量为
w=[0.126 0.091 0.060 0.066 0.099 0.093
0.074 0.061 0.067 0.124 0.051 0.088]
步骤 3规范化处理原始主客观信息后得到规范化群决策矩阵如表10所示。
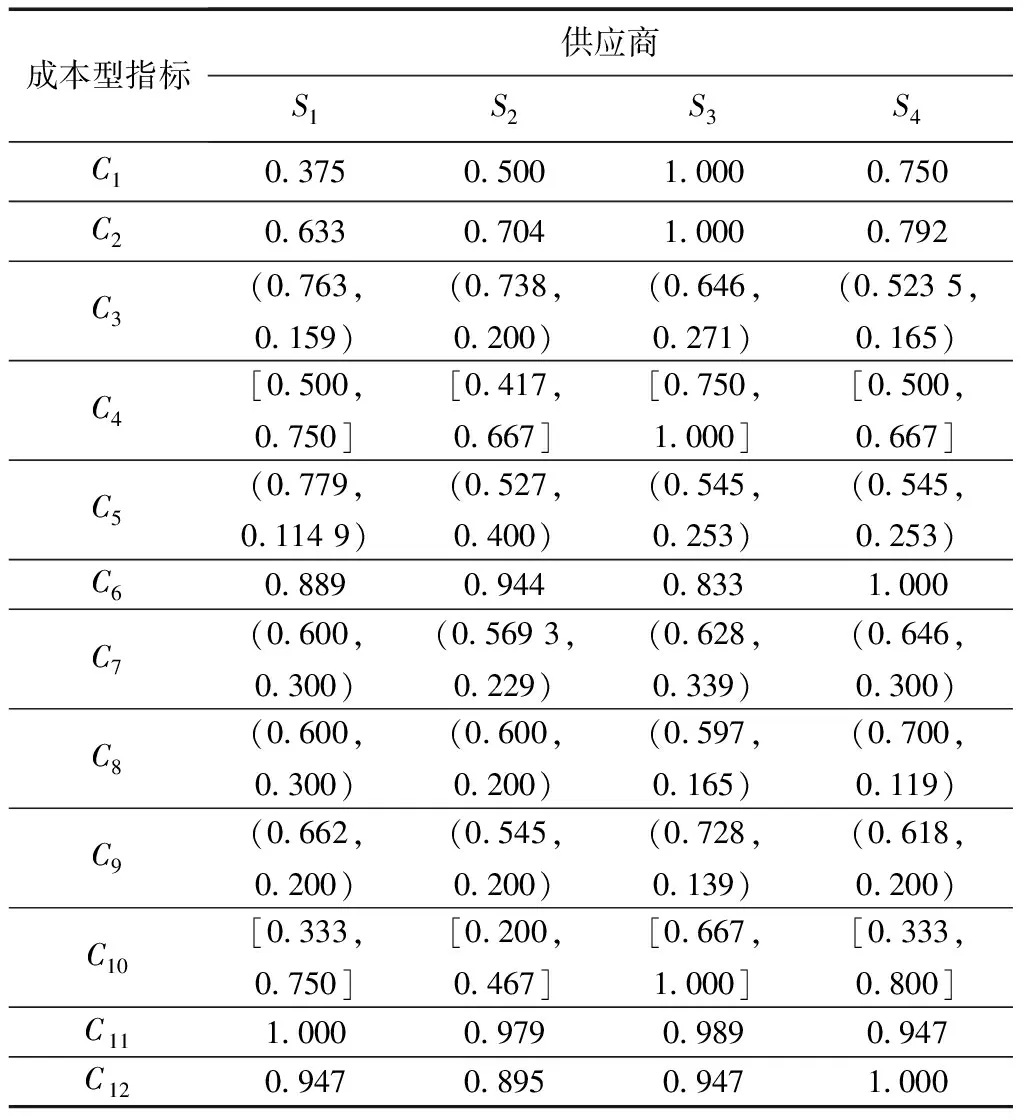
表10 规范化群决策矩阵
确定正负理想方案向量:
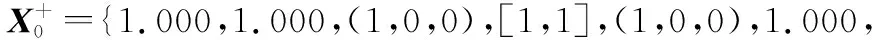
(1,0,0),(1,0,0),(1,0,0),[1,1],1.000,1.000}
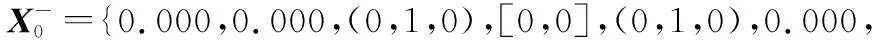
(0,1,0),(0,1,0),(0,1,0),[0,0],0.000,0.000}
步骤 4计算正负理想方案向量与各个方案决策向量之间的绝对差值,令α=0.5,根据灰关联系数的计算公式,得到正负灰关联矩阵:
代入指标权重可以得到加权正负灰关联决策矩阵,根据指标权重计算灰关联投影矢量:
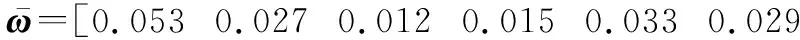
0.018 0.012 0.015 0.051 0.009 0.026]
步骤 5根据灰关联投影矢量与加权正负灰关联决策矩阵中的各个方案向量(行向量),可以求出不同方案的灰关联投影值与灰关联投影系数如表11所示。
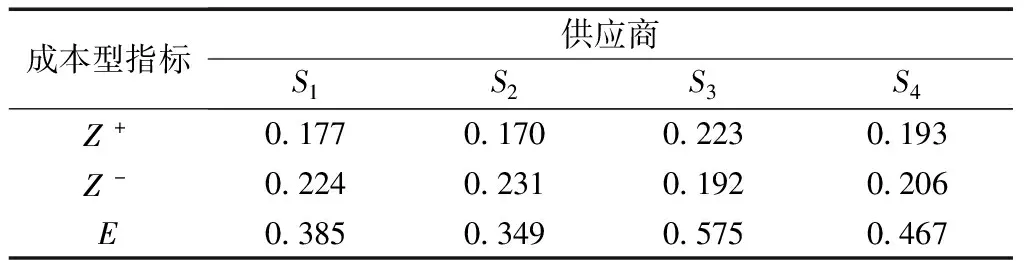
表11 各方案的Z+, Z-, E值
由表11可知,无论是根据优势方案还是劣势方案进行排序,其结果与依据灰关联投影系数值得到最终的优劣排序保持一致,均为S3>S4>S1>S2,S3均为最优方案。但是灰关联投影系数的差异性更加明显,其区分不同方案优劣性的能力更强。
4.2 对比分析
现有文献模型中,对群决策的关联性及指标关联性考虑还不够充分,如文献[22]中的模型根据信息熵原理来建立信任函数确定决策权重来集结群决策信息,通过熵值法来确定指标的客观权重,从而避免指标间的属性转换。将其方法应用到本文案例中得到如表12所示的结果。

表12 不同评价模型的排序结果
从最终的排序结果来看,文献[22]与本文在对S1的评价偏差较大。一方面,在群决策信息集结时,其未考虑到专家间的偏好关联,使得专家e2和e3的权重偏大,导致主观信息的集结产生一定偏差。另一方面,在对评价指标的权重确定时,其主要是基于熵值法来计算不同评价指标的客观权重,并未考虑不同指标间的关联性,这亦是最终的评价结果存在差异性的原因。本文通过λ-Shapley模糊测度来衡量专家间的模糊关系,并引入群组DEMATEL到决策模型中来进行指标间的关联性评价和权重确定,使得多属性群决策模型更加符合实际问题中决策者对复杂事物的评价和感知。
4.3 敏感性分析
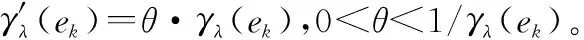
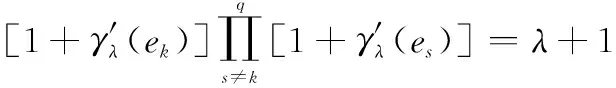
(45)
由于γλ(ek)、θ、λ均已知,代入式(45)即可求得φ值。分别对3个专家模糊测度进行扰动,θ依次取为0.4、0.5、0.6、0.7、0.8、0.9、1.1、1.2、1.3、1.4、1.5和1.6共进行36次试验,计算不同方案最终的灰关联投影系数,得到如图2所示结果。由图2可见,专家模糊测度的变化使得不同方案的最终评价值变化幅度较大,是因为本文模型在权重和指标评价时都是采用的相同的专家群体,专家个体的模糊测度确定会对结果造成较大的影响。但是,在36次试验中模型最终得到的最优方案稳定性较好(仅有2次改变了最优方案,占试验总体5.56%),且在实际评价中,评价专家群体能同时参与定性指标的评价打分和对指标间的影响关系分析,更加适用于装备采购供应链环境中的管理和决策,有利于提高军方在供应链质量管理和监督中的主导地位。
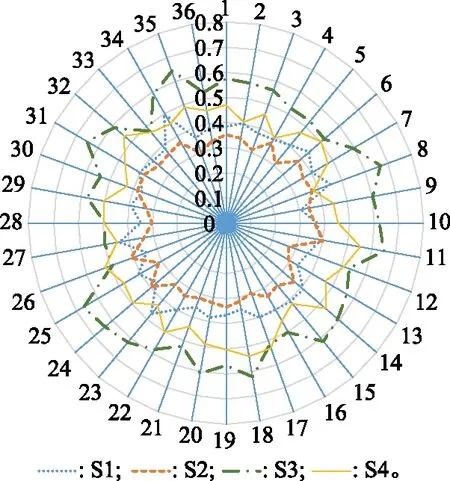
图2 基于专家模糊测度的敏感性分析
5 结束语
装备采购供应链运作初期,构建合理科学的供应商质量绩效评价模型是军方监测装备承制单位的质量体系运行和产品生产质量状况、促进承制单位竞争性发展的重要手段。利用专家模糊评价与群体评价的偏差程度和不确定程度来确定专家评价的模糊测度,并通过引入Shapley函数到Choquet积分算子中,使专家信息集结方法更客观。通过群组DEMATEL进行指标的影响度评价,可以在分析不同指标相互影响关系的基础上进行指标权重确定;利用灰关联投影法集结不同类型评价信息,避免不同类型数据之间的不可公度带来的影响。算例表明,本文评价模型能有效应对混合型模糊信息条件下的多属性群决策问题,在装备采购供应商的质量绩效评价中具有较强的实用性。
