基于加权l1范数优化的双基地ISAR稀疏成像算法
2021-04-13薛东方朱晓秀胡文华郭宝锋曾慧燕
薛东方, 朱晓秀, 胡文华, 郭宝锋, 曾慧燕
(陆军工程大学石家庄校区, 河北 石家庄 050003)
0 引 言
双基地逆合成孔径雷达(inverse synthetic aperture radar, ISAR)[1-3]继承了双基地雷达的独特优势,利用收发分置模式增强了系统灵活性,提高了成像概率,对目标的监视、跟踪、成像与识别以及赢得未来战争都具有非常重要的意义[4-6]。
由于双基地的收发分置特性以及对目标观测时需要不断切换波束,在观测过程中容易引起回波缺失进而造成稀疏孔径[7-9]。由于ISAR图像的空域稀疏性[10-12],不少学者将压缩感知(compressed sensing,CS)理论[13-16]应用到了ISAR成像中,以提高成像质量。在重构算法的选择上,贪婪迭代类算法虽然原理简单,易于实现,但重构精度不高,特别是在低信噪比(signal-to-noise ratio, SNR)条件下,算法的重构性能易受影响。
文献[17]利用贝叶斯解释,假设目标图像各像元稀疏同分布,将ISAR成像问题转化为最大后验概率估计问题,并等价于l1范数优化问题进行求解,实现了ISAR图像重构,在低SNR条件下有较好的聚焦效果和噪声抑制能力。文献[18]将该方法应用到稀疏孔径当中,利用稀疏孔径数据得到了聚焦良好的ISAR图像,同时具有有效的噪声抑制效果。但该算法在实现过程中假设图像各像元服从独立同分布的稀疏先验,即假设目标图像中的所有元素服从同一Laplace分布,并没有区分各像元的幅度大小。然而在ISAR成像过程中,目标通常靠近零多普勒成像,由于相邻散射点具有相近的幅度值,若能利用这种能量聚集和目标的几何结构特性,必将有效提高成像性能[19]。在贝叶斯估计问题中,如何利用目标信号的特征则表现为如何选择一个更符合目标特性的先验模型。为有效利用目标的能量聚集和结构特性,在建立稀疏先验模型时将目标图像中的不同元素加以区别,假设它们独立服从不同的Laplace分布,通过设置不同大小的尺度系数有效区分目标散射中心和噪声,进一步提高算法的噪声抑制性能和有效散射点提取能力。
因此,为充分利用图像的像元信息以提高重构质量,本文提出一种基于加权l1范数约束最优化的双基地ISAR稀疏孔径成像算法。首先,假设各像元稀疏非同分布,利用贝叶斯准则和最大后验概率估计将双基地ISAR稀疏孔径成像问题转化为加权l1范数约束问题,建立成像模型;其次,利用柯西-牛顿算法进行加权l1范数约束最优化问题的求解,实现目标图像重构,最后利用仿真实验验证算法的有效性和优越性。
1 稀疏孔径成像模型
1.1 双基地ISAR成像信号模型
双基地ISAR成像的几何模型的建立与文献[20]中相同,假设雷达发射线性调频信号,脉冲重复周期为Tr,则信号可表示为
(1)
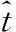
经包络对齐和相位校正后的双基地ISAR回波的可近似为
(2)
式中,σP为散射点P的信号复幅度;xP和yP分别为散射点P的坐标;θ(tm)和β(tm)分别为成像期间内的旋转角度和双基地角,随慢时间tm变化。
为了避免双基地角时变引起越的分辨单元徙动和图像畸变,需要构造相应的补偿相位进行相位补偿[21]。构造的补偿项为φcomp=exp[j(4πfc/c)yPcosθ(tm)cos(β(tm)/2)],得到相位补偿后的一维距离像表达式为
(3)
假设在距离单元(2yP/c)cos(β(tm)/2)内有Q个强散射点,则此单元的回波信号可表示为
(4)
式中,aq为第q个散射点的信号复幅度。
1.2 回波的稀疏表示
假设全孔径回波信号中共包含L个脉冲视角,累积转角为Δθ,构造稀疏基矩阵Fall将二维成像场景离散化为N个距离单元和M个多普勒单元,则稀疏基矩阵可构造为
(5)
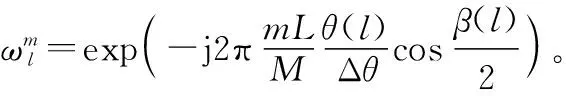
考虑到实际噪声的存在,则双基地ISAR全孔径回波可稀疏表示为
Sall=FallA+ε0
(6)
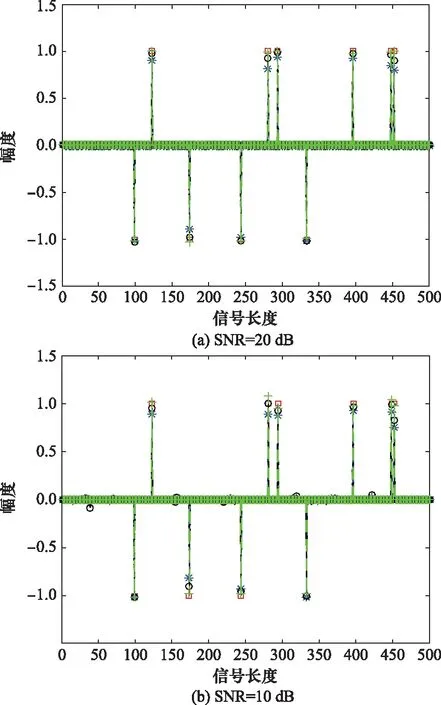
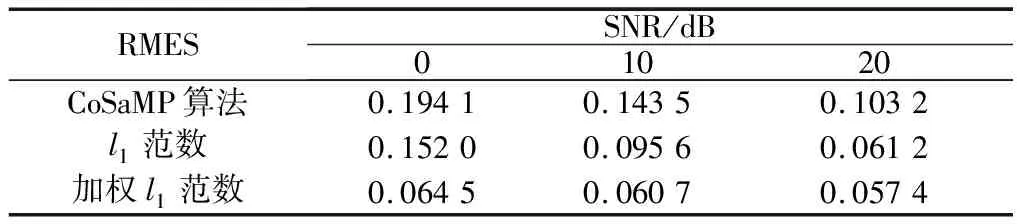
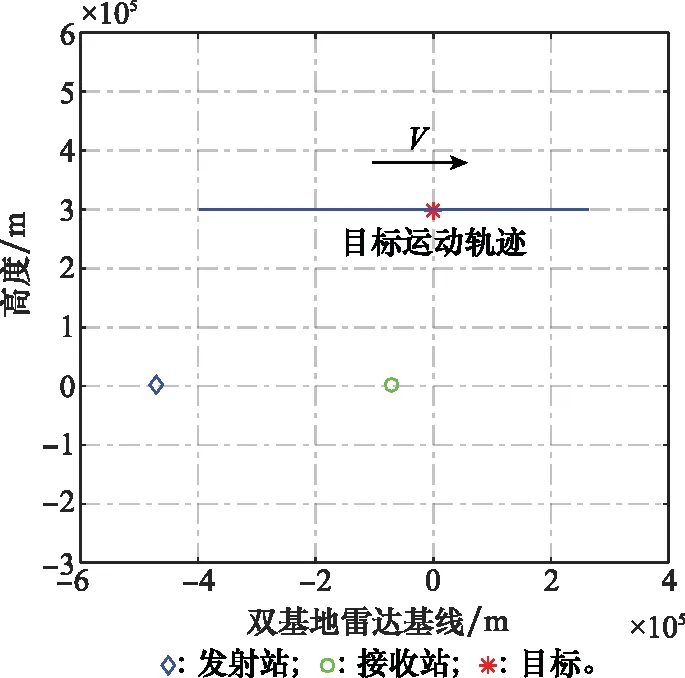
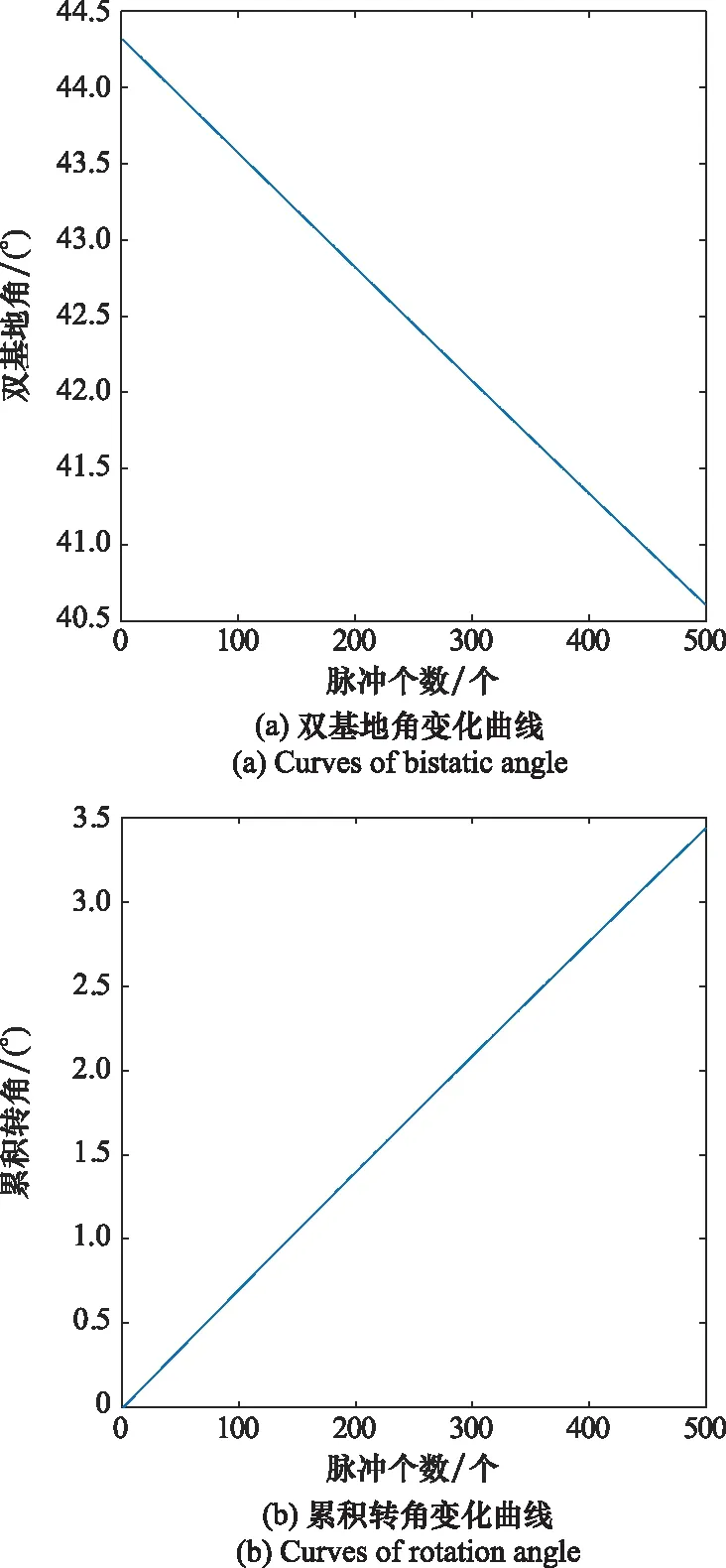
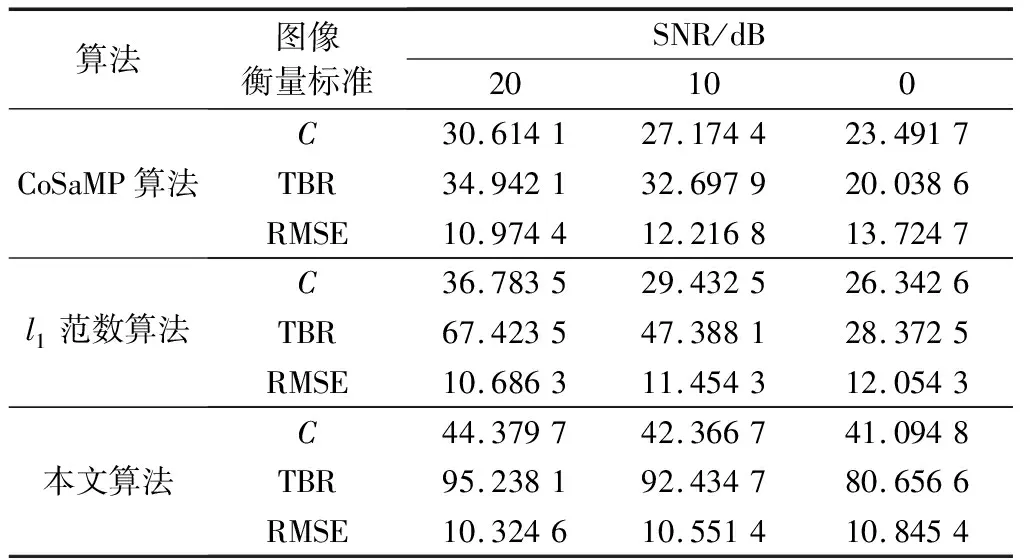
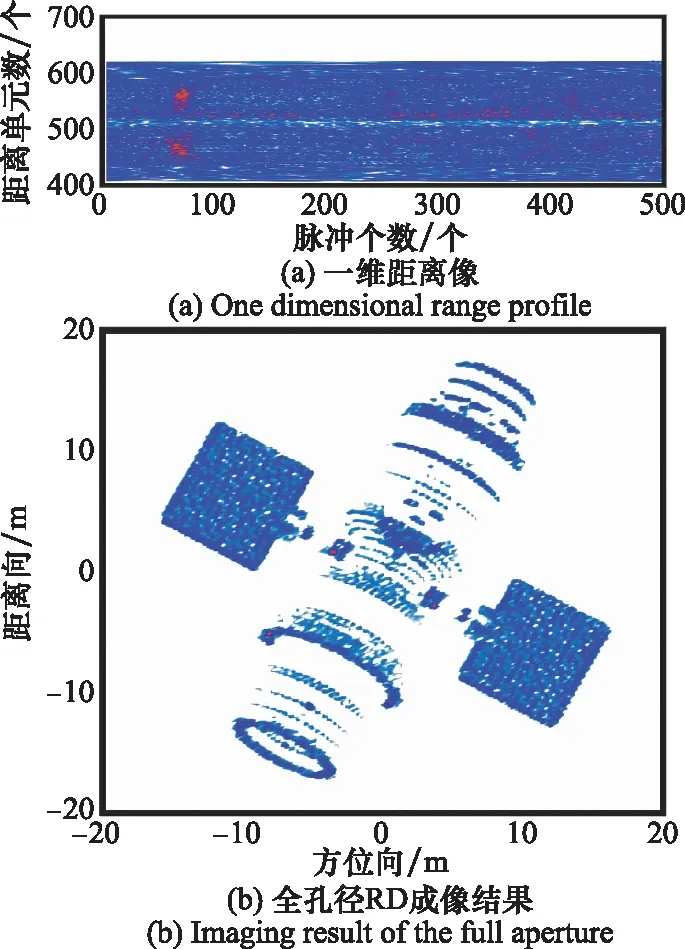
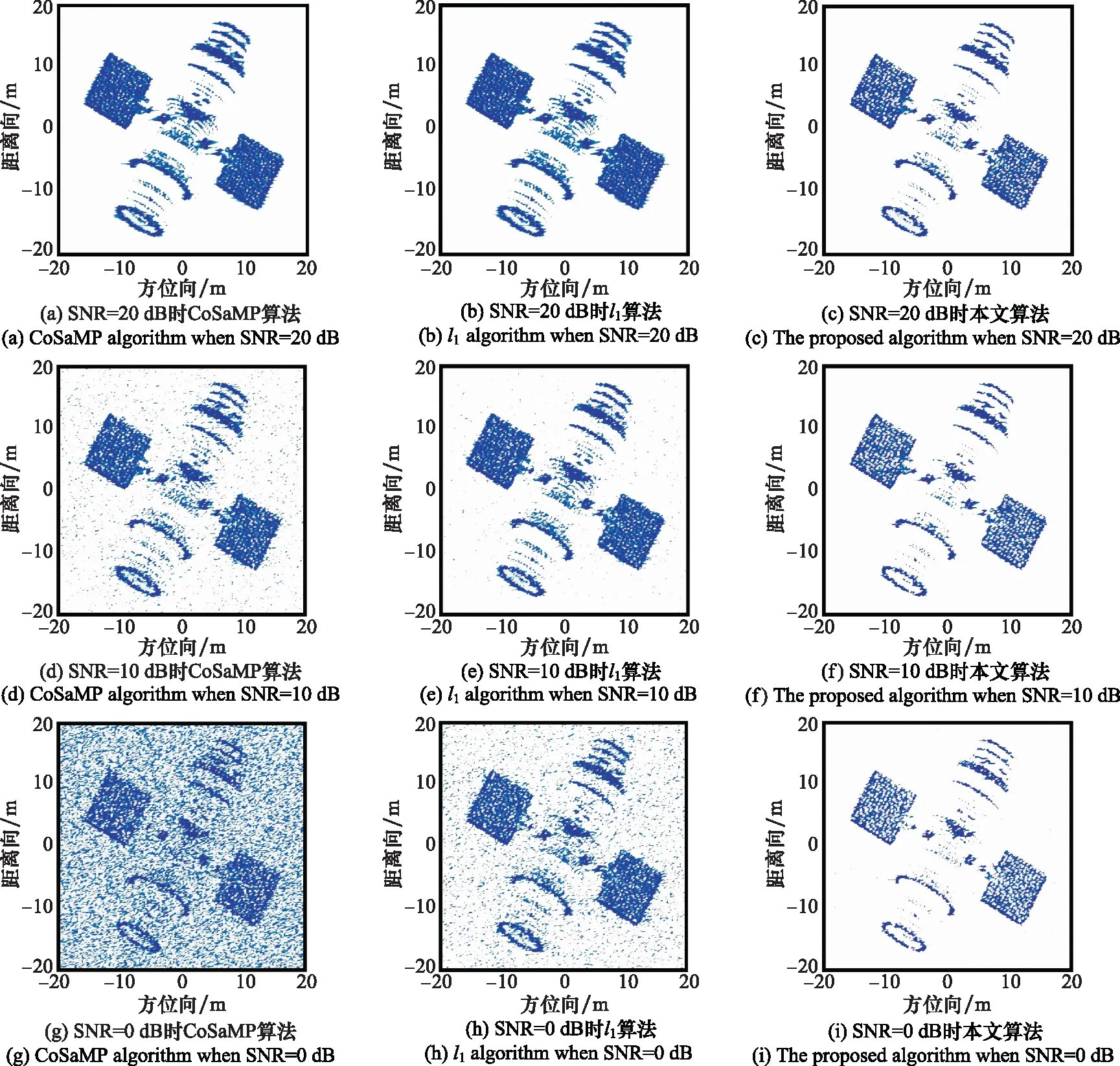
式中,Sall表示经过运动补偿和相位补偿后的全孔径二维回波数据;ε0为噪声;A为需要求解的目标图像。假设在稀疏孔径条件下,S表示融合的有效孔径回波数据,共包含J(J S=TSall+ε=TFallA+ε=FA+ε (7) 式中,T为有效数据选择矩阵;F为在稀疏基矩阵;ε为J×N复噪声矩阵。为方便求解,将式(7)矢量化表示为 (8) 式中,sn、εn和an分别表示第“n”个距离单元对应的回波数据矢量、噪声矢量和目标图像矢量。 假设ε是复Gaussian白噪声,其元素随机且独立同分布,服从复Gaussian分布,均值为0,方差为σ2,则ε的概率密度函数为 (9) (10) 为了更好地利用图像稀疏信息,利用Laplace概率分布表征目标的稀疏性,假设目标图像各像元amn独立服从不同的Laplace先验分布[22],则 (11) (12) (13) (14) 将式(10)和式(12)代入式(14),可得 (15) 式(15)的目标图像求解公式表示,通过引入非同分布稀疏先验模型,即利用Laplace先验的尺度系数γmn。若散射点幅值较大,则γ值设置较小,以提高其出现大值的可能性,若散射点幅值较小或为噪声空间,则γ值设置较大,对其实现抑制效果。相比于没有区分像元幅度大小的l1范数约束最优化算法[17],这种区分了各像元幅度大小的加权l1范数约束最优化算法会带来更好的成像效果。 要根据式(15)求解得到目标图像,首先需要求解Laplace先验的尺度系数γmn,然后再求解l1范数最优化问题。 2.2.1 尺度系数求解 对于尺度系数γmn的取值大小,可用最大似然的方法进行估计,为方便求解,在对数域进行估计,式(12)的对数似然函数为 (16) 对γmn求导并等于零,可得 (17) 得到尺度系数γmn的估计为 (18) 由式(18)可以看出,尺度因子的大小与目标图像各像元的幅度有关,即加权l1范数约束最优化算法是通过目标图像中非零元大小来确定权值大小,因此在成像过程中利用了非零元幅度的大小差异,更有利于提高成像精度和抗噪能力。 2.2.2 优化问题求解 基于加权l1范数约束最优化算法主要是对式(15)表示的最优化问题进行求解,可利用柯西-牛顿迭代法进行求解,并采用共轭梯度算法[24]加快收敛速度,下面给出具体的求解过程。 由于式(15)中的l1范数在零点处不可导,首先可对其引入平滑近似[25]: (19) 式中,ς是一个很小的非负常数,则式(15)中的优化问题可近似表示为 (20) (21) 式中, (22) (23) 式中,β为迭代步长。将式(21)代入式(23)并令β=1,可得到目标图像矢量的估计值: (24) 综上所述,基于加权l1范数约束最优化成像算法实现流程如图1所示。主要实现步骤如下。 图1 基于加权l1范数约束最优化算法实现流程 由于加权l1范数约束的权值是由迭代过程中目标图像的像元幅度决定的,利用较大的尺度系数对噪声像元进行约束,利用较小的尺度系数对强散射点像元进行约束,能在提高强散射点出现概率的同时对噪声实现更好的抑制作用。相比于像元稀疏同分布方法而言,能有效提高成像精度和抗噪声干扰能力,更有利于提高成像质量。 本部分利用两个仿真实验验证加权l1范数约束算法的有效性和优越性。首先,在不同SNR条件下,利用本文所提算法与l1范数约束最优化算法以及贪婪算法中的CoSaMP算法[26]对一维信号进行稀疏重构,通过对比其重构性能,验证所提算法的优越性。然后,分别利用这三种算法对方位向稀疏孔径的双基地ISAR进行成像,以验证算法的双基地ISAR成像性能。 图2 不同SNR条件下信号重构结果 可以看出,在SNR=20 dB的情况下,3种算法都能准确地重构出非零元素的位置,但CoSaMP算法所得结果的非零元素幅度值略小于原始值,而l1范数约束最优化算法和加权l1范数约束最优化算法所得结果的非零元素幅度基本与原始值一致。在SNR=10 dB的情况下,CoSaMP算法和l1范数约束最优化算法虽也能准确地重构出非零元素位置,但其幅度值与原始值相差较多,导致重构误差较大,而且在其他零元素位置会出现幅值较小的虚假点,而此时加权l1范数约束最优化算法所得结果的非零元素幅度仍与原始值基本一致。在SNR=0 dB的情况下,CoSaMP算法和l1范数约束最优化算法受噪声水平影响较大,重构结果中有大量的噪声没有被抑制,出现了较多的虚假点,而且在重构幅度上与原始信号相差较大,导致重构误差较大,而加权l1范数约束最优化算法仍能较为准确地重构出非零元素的位置和幅度,且噪声抑制效果较好,体现了算法有较强的抗噪性能。 为进一步比较算法的重构性能,采用均方根误差均方根误差(root mean square error, RMSE)衡量信号的重构效果,其定义为 (25) 在3种SNR条件下,利用3种算法恢复信号时的RMSE值如表1所示。可以看出,在相同的SNR条件下,加权l1范数约束最优化算法的RMSE值最小,其次是l1范数约束最优化算法,CoSaMP算法的RMSE值较大。随着SNR减小,CoSaMP算法和l1范数约束最优化算法的RMSE值增大较多,性能下降较快,而加权l1范数稀疏约束最优化算法的RMSE值变化较小,说明加权l1范数约束最优化算法具有更好的强散射点提取能力和抗噪声干扰能力。 表1 信号重构的RMSE值 4.2.1 仿真场景和参数设置 双基地ISAR仿真场景如图3所示,假设双基地基线长度为400 km,目标在300 km的高度以3 km/s的速度沿基线方向由发射站向接收站匀速运动,运动轨迹为图中粗横线所示,成像起点运动轨迹高度上距接收站右侧水平距离70 km处。目标的散射点模型如图4所示,该模型由100个散射点组成,成像的仿真参数设置如表2所示。假设成像观测时间为10 s,累积脉冲数为500个,在此成像段内双基地角和累积转角变化曲线如图5所示,其中,图5(a)为双基地角变化曲线,图5(b)为累积转角变化曲线。 图3 仿真场景 图4 散射点目标模型 表2 成像参数设置 图5 双基地角和累积转角变化曲线图 4.2.2 算法的抗噪性能验证 为比较算法在双基地ISAR稀疏孔径条件下的成像性能,利用CoSaMP算法、l1范数约束最优化算法和本文所提的加权l1范数约束最优化算法实现双基地ISAR稀疏孔径成像。假设方位向孔径随机缺失50%,在SNR为20 dB、10 dB和0 dB条件下分别利用3种算法实现双基地ISAR稀疏孔径成像,成像结果如图6所示。从成像结果可以看出,当SNR较高(如20 dB)时,利用3种CS重构算法均能较好地实现双基地ISAR稀疏孔径成像,但随着SNR降低,基于CoSaMP算法和l1范数约束最优化算法的成像结果质量明显有所下降,其中利用l1范数约束最优化算法成像结果稍好于CoSaMP算法,而基于加权l1范数约束最优化算法仍能得到较高质量的ISAR图像,特别是当SNR为0 dB时,利用CoSaMP算法成像时对噪声抑制能力不强,出现了较多的干扰噪点,严重影响成像质量,利用l1范数约束最优化算法成像虽效果比CoSaMP算法较好,但存在“虚影”和少许噪点,成像质量不佳,而加权l1范数约束最优化算法在低SNR条件下仍能得到较好的成像结果。 图6 不同SNR条件下简单目标成像结果 为方便直观比较算法性能,采用目标背景比(target-to-background ratio,TBR)、图像对比度C和RMSE作为图像衡量标准,其中TBR、C和RMSE的定义可表示为 (26) 式中,T和B分别表示目标和背景支撑区,将目标能量较为聚集的区域作为目标支撑区,其余单元作为背景支撑区;E(·)表示取平均操作。TBR能有效表征目标图像的能量聚焦程度,可以评价目标图像的噪声抑制能力和聚焦能力,值越大越好;图像对比度可以评价目标图像的整体聚焦质量,也是值越大越好;均方根误差可评价算法的重构精度,值越小表示重构精度越高。利用CS算法重构出的图像衡量指标值如表3所示。 表3 不同SNR条件下成像结果衡量指标对比 从表3中的数据可以看出,随着SNR减小,3种算法成像结果的TBR值和图像对比度值也减小,RMSE增加,且在相同的SNR条件下,利用加权l1范数约束最优化算法所得图像的TBR值和图像对比度值最大,RMSE值最小,其次是l1范数约束最优化算法,而利用CoSaMP算法的TBR值和图像对比度值最小,RMSE值最大,说明在低SNR条件下,利用加权l1范数约束最优化算法能比其他两种算法得到更高质量的图像,实现更高精度的重构,体现了本文所提算法的优越性。 为进一步验证算法的成像性能,本小节采用复杂的电磁散射模型进行仿真实验。 4.3.1 目标模型 采用典型的卫星目标为仿真目标,其计算机辅助设计(computer aided design, CAD)模型如图7所示。利用物理光学法,获得目标的电磁散射特性分布数据[27],并利用该数据进行后续的仿真实验。仿真场景和参数设置与第4.2.1节一致,对回波数据进行平动补偿等处理后,可得到如图8所示的一维距离像和RD算法成像结果。 图7 典型卫星目标CAD模型 图8 全孔径一维距离像及RD成像结果 4.3.2 算法的抗噪性能验证 利用CoSaMP算法、l1范数约束最优化算法和本文所提的加权l1范数约束最优化算法实现双基地ISAR稀疏孔径成像。为比较算法的抗噪性能,假设方位向孔径随机缺失50%,在SNR为20 dB、10 dB和0 dB条件下分别利用3种算法实现双基地ISAR稀疏孔径成像,成像结果如图9所示。 图9 不同SNR条件下复杂目标成像结果 从成像结果可以看出,在相同的SNR条件下,l1范数约束最优化算法的成像结果稍好于CoSaMP算法,而基于加权l1范数约束最优化算法所得的成像结果最好,特别是在低SNR条件下,基于CoSaMP算法和l1范数约束最优化算法的成像结果质量明显下降,出现了较多的干扰噪点,利用本文所提的加权l1范数约束最优化算法能比其他两种算法得到更高质量的图像,重构图像结果中背景干净,达到了较好的噪声抑制效果,体现了所提算法在抗噪性能方面的优越性。 为提高低SNR条件下双基地ISAR稀疏孔径成像质量,提出了一种基于加权l1范数优化的高分辨成像算法。在构建先验模型时,以加权的思想,假设各像元稀疏非同分布,充分利用了双基地ISAR成像时目标的能量聚集特性和结构特性。在求解时,利用贝叶斯准则和最大后验概率估计将双基地ISAR稀疏孔径成像问题转化为加权l1范数约束问题,采用柯西-牛顿算法进行求解,实现目标图像重构。仿真实验表明,所提算法具有更好的强散射点提取能力和抗噪声干扰能力,在低SNR条件下能实现更好的稀疏重构。但受实验条件限制,本文的实验均是在仿真数据基础上进行的,下一步需要利用微波暗室测量数据或外场实测数据进一步验证算法性能。2 算法实现
2.1 模型转化



2.2 算法求解



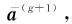
3 算法流程

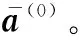
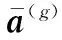

4 仿真实验与分析
4.1 一维信号稀疏重构性能验证
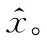
4.2 简单目标双基地ISAR稀疏成像性能仿真



4.3 复杂目标双基地ISAR稀疏成像性能仿真

5 结 论
