Property Preservation of Petri Synthesis Net Based Representation for Embedded Systems
2021-04-13ChuanliangXiaandChengdongLi
Chuanliang Xia and Chengdong Li
Abstract—Embedded systems have numerous applications in everyday life. Petri-net-based representation for embedded systems (PRES+) is an important methodology for the modeling and analysis of these embedded systems. For a large complex embedded system, the state space explosion is a difficult problem for PRES+ to model and analyze. The Petri net synthesis method allows one to bypass the state space explosion issue. To solve this problem, as well as model and analyze large complex systems, two synthesis methods for PRES+ are presented in this paper. First,the property preservation of the synthesis shared transition set method is investigated. The property preservation of the synthesis shared transition subnet set method is then studied. An abstraction-synthesis-refinement representation method is proposed. Through this representation method, the synthesis shared transition set approach is used to investigate the property preservation of the synthesis shared transition subnet set operation. Under certain conditions, several important properties of these synthetic nets are preserved, namely reachability, timing,functionality, and liveness. An embedded control system model is used as an example to illustrate the effectiveness of these synthesis methods for PRES+.
I. INTRODUCTION
EMBEDDED systems are ubiquitous in almost all devices used today, including mobile telephones, network switches, household appliances, and controllers of the internet of things (IoT). Such systems are an important part of large complex networks and often include both software and hardware elements. Real-time behavior, correctness, and good reliability are vital requirements for successful embedded systems [1]. Many models have been proposed to describe such systems, including finite state machines, data flow graphs, and Petri nets.
Petri nets constitute a high-performing model, widely used in many fields of science. The model can be used to express concurrency, synchronization, sequential actions, and nondeterminism when designing certain systems. Petri-net-based representation for embedded systems (PRES+) have been proposed for the design and verification of embedded systems[2]. Using PRES+ supports allows for a precise representation of embedded systems, improves expressiveness, and captures timing information.
The PRES+ model is important for the modeling, analysis,and verification of embedded systems [2]–[8]. In order to design and verify these systems, Cortés et al. [2] presented a formal computational model based on PRES+. An industrial example was also provided to illustrate the efficiency of the PRES+ method. To improve its verification efficiency, a translation algorithm from the PRES+ model to a finite state machine with the datapath model was proposed [3]. For systems specified in PRES+, Karlsson et al. [5] put forward a method to integrate them with component-based system level design. The model utilized was a mobile telephone system,consisting of seven connected components, which were modeled in PRES+. The properties of reachability and timing were then verified. Xia [6] proposed several reduction rules to improve the verification efficiency of PRES+. Under some constraints, the properties of reachability, functionality, and timing were preserved.
However, the state space explosion problem for PRES+struggles to specify and analyze large, complex embedded systems. This problem is of exponential complexity and decreases the modeling and verification abilities of PRES+.
The state space explosion problem is due to the absence of abstraction and compositionality mechanisms. Many researchers have used transformation approaches to resolve the state space explosion problem for Petri nets. It is essential to neither destroy nor create properties under investigation when establishing transformations. Three popular transformations exist among the literature, namely reduction [6], [9]–[16],refinement [7], [17]–[22], and synthesis [23]–[36].
Petri-net-based synthesis is an effective approach to system design and verification. The synthesis method can create a system from several component modules in such a way that the system can be effectively analyzed for design correctness.A review of some approaches in the synthesis of Petri nets is provided below.
A Petri-net-based synthesis methodology to resolve the usecase driven system design problem was proposed in [23].Zhou et al. [24] presented a hybrid synthesis approach for manufacturing systems by using parallel and sequential mutual exclusions. For distributed liveness-enforcing supervisors of automated manufacturing systems, Hu et al.[25] focused on a synthesis method that allows both multiple resource acquisition operations and flexible process routes.Best et al. [26] characterized the reachability graph of a Petri net marked graph. This work described procedures to synthesize a marked graph solving a labeled transition system benefiting from characterizing properties. Pouyan et al. [27]classified synthesis methods into the following groups: topdown techniques, hybrid approaches, knitting techniques, and bottom-up techniques. For systems of simple sequential several algorithms to synthesize recovery subnets and monitors. Certain conditions were presented to impose on a synthesis shared pp-type subnet that ensures the preservation of the liveness, boundedness, and reversibility properties [29].Xia [30] investigated a shared pb-type subnets synthesis approach for place/transition (PT) nets. This synthesis method preserves the properties of liveness and boundedness. Liu et al.[31] proposed a synthesis approach of supervisors for flexible manufacturing systems modeled by a class of generalized Petri nets. An effective approach has also been presented for the synthesis of compact and decentralized supervisors for Petri net (PN) systems [31]. Jiao et al. [32] proposed a synthesis approach to merge a set of places of asymmetric choice nets and presented the constraints to preserve the siphon trap (ST) property, reversibility, liveness, and boundedness. For systems specified in hybrid Petri nets,Basile et al. [33] proposed an automated synthesis method for the sequencing of the activities of a robotic cell for the aircraft industry. Both static and behavioral control specifications can be considered using this method [34]. Additionally, Hu et al.[35] proposed a kind of logic Petri net synthesis method.
To solve the PRES+ state space explosion problem, as well as model, analyze, and verify large and complex embedded systems, two kinds of synthesis approaches are investigated in this paper. Compared with some synthesis methods for ordinary Petri nets [23], [29], time Petri nets, and colored nets,these approaches effectively represent important characteristics of embedded systems such as reachability,functionality, and timing. In [7], an approach for expanding the PRES+ model to the desired level of detail was provided,and a transition refinement method was proposed.Reachability, timing, functionality, liveness and boundedness preservation of the refined PRES+ model have also been investigated. To improve the verification efficiency of PRES+, Xia [6] presented a set of reduction rules. Under certain constraints, the reduced PRES+ model preserves reachability, timing, and functionality. A sharing synthesis operation for PRES+ and its liveness and boundedness preservation have been investigated in [8].
The principal motivation of this paper is to solve the synchronous problem in embedded systems, and the embedded subsystem sharing problem. The subsystem-sharing problem is formulated as a problem of merging several sets of subsystems into transition sets. Some constraints for ensuring that these synthesis methods preserve reachability, timing,functionality, and liveness are obtained in this work. The results are then applied to the verification of the modeling processes with resources (S3PR), Liu et al. [28] proposed problem of embedded systems. First, a synthesis shared transition set for PRES+ is presented, and the property preservation of the method is investigated. Following this, the synthesis shared-transition-set technique of PRES+ is used to investigate the synthesis shared-transition-subnet-set technique by adopting the abstraction-synthesis-refinement representation method. Results obtained are useful for investigating the properties of PRES+ synthesis nets, and establishing models for large and complex embedded systems.
The remainder of this paper is organized as follows. Some preliminaries of PRES+ are proposed in Section II. The synthesis shared-transition-set approach and the synthesis shared-transition-subnet-set approach of PRES+ are presented in Section III. The abstraction-synthesis-refinement representation method is proposed in Section IV, and the preservation of reachability, timing, and functionality is investigated in Section V. Liveness preservation by these two synthesis approaches is discussed in Section VI. A case example is proposed in Section VII to illustrate the effectiveness of the proposed synthesis methods. Finally, conclusions are presented in Section VIII.
II. PRELIMINARIES
In this section, the fundamentals of PRES+ are provided as a foundation for the rest of this article. A more general discussion on PRES+ can be found in [2].
Definition 1: A PRES+ model is N=(P,T,I,O,M0), where P={p1,p2,...,pm} is a set of places, T ={t1,t2,...,tn} is a set of transitions, I ⊆P×T is a set of input arcs, O ⊆T×P is a set of output arcs, and M0is the initial marking. k =
Fig.1 shows an example of the definitions of the PRES+model presented in this section. For the example, we have
P={p1,p2,p3,p4,p5} , T ={t1,t2,t3,t4} , I={(p1,t1),(p2,t2),(p3,t3),(p4,t3),(p5,t4)} , and O={(t1,p2),(t1,p3),(t2,p4),(t3,p5),(t4,p1)}.
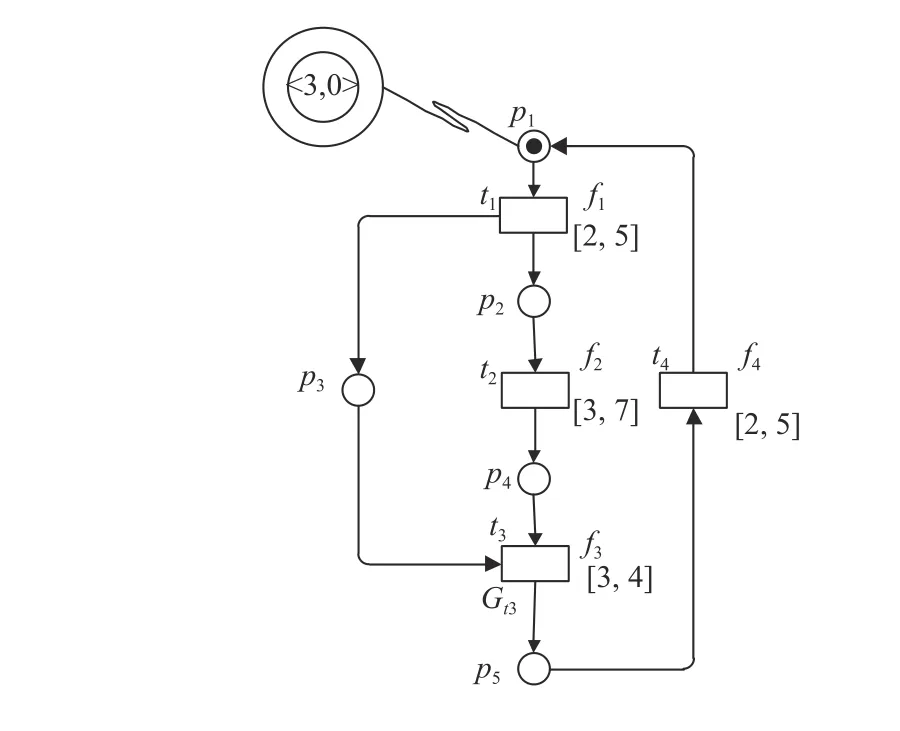
Fig.1. A simple PRES+ model.
Definition 2: A marking is an assignment of tokens to places. The marking M(p) of a place p ∈P can be represented as a set over Ep⊆{







Fig.4. Subsystem N1.
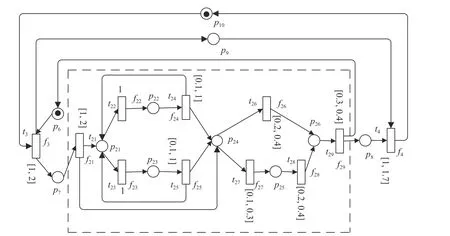
Fig.5. Subsystem N2.
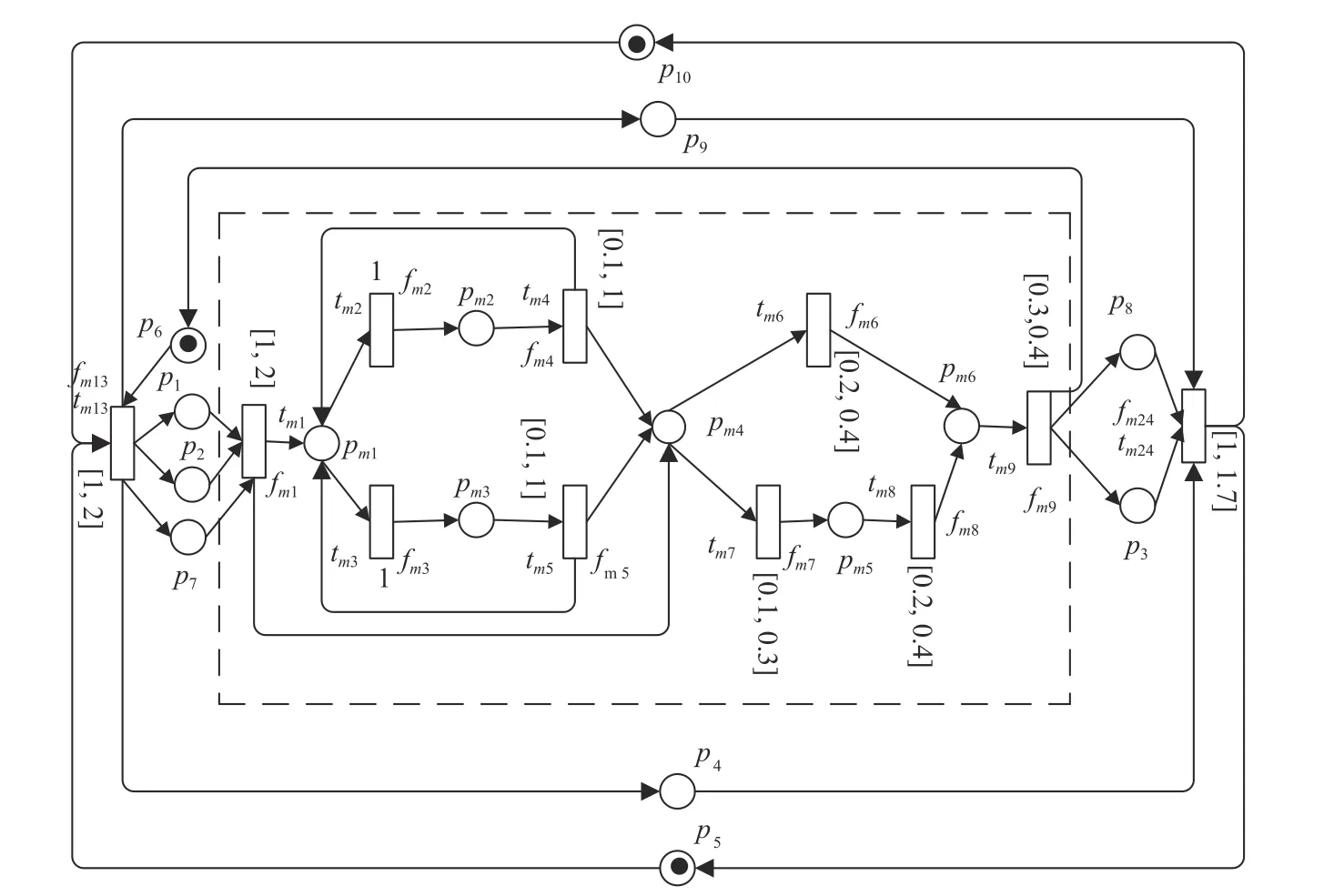
Fig.6. Synthesis control system N.


VIII. CONCLUSIONS
Embedded systems have many applications in everyday life.Petri-net-based representation for embedded systems (PRES+)is an excellent tool to model and verify embedded systems.However, the state space explosion is a serious problem for using PRES+ to model and analyze large complex embedded systems. The Petri net synthesis method can avoid the state space explosion problem, and in this paper, the preservation of properties of the synthesized PRES+ model was investigated to help solve this problem. The synthesis shared transition set approach and the synthesis shared transition subnet set approach of the PRES+ method were proposed. Under several additional conditions, reachability, functionality, timing, and liveness were preserved after merging some transitions or transition subnets of PRES+ models. The results of this paper can be successfully applied to solve design problems in embedded control systems of intelligent buildings and manufacturing engineering.
Further research is required to investigate other more general synthesis operations for PRES+ and their applications.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Residual-driven Fuzzy C-Means Clustering for Image Segmentation
- Decoupling Adaptive Sliding Mode Observer Design for Wind Turbines Subject to Simultaneous Faults in Sensors and Actuators
- Task Scheduling for Multi-Cloud Computing Subject to Security and Reliability Constraints
- Vibration Control of a High-Rise Building Structure: Theory and Experiment
- Fixed-Time Output Consensus Tracking for High-Order Multi-Agent Systems With Directed Network Topology and Packet Dropout
- Dynamic Evaluation Strategies for Multiple Aircrafts Formation Using Collision and Matching Probabilities
