Vibration Control of a High-Rise Building Structure: Theory and Experiment

Yuhua Song, Student Member, IEEE, Wei He, Senior Member, IEEE, Xiuyu He, Member, IEEE, and Zhiji Han

Abstract—In this study, an innovative solution is developed for vibration suppression of the high-rise building. The infinite dimensional system model has been presented for describing high-rise building structures which have a large inertial load with the help of the Hamilton’s principle. On the basis of this system model and with the use of the Lyapunov’s direct method, a boundary controller is proposed and the closed-loop system is uniformly bounded in the time domain. Finally, by using the Smart Structure laboratory platform which is produced by Quancer, we conduct a set of experiments and find that the designed method is resultful.

I. INTRODUCTION

DUE to the rapid growth of urban population, the number of high-rise buildings continues to grow to satisfy the demands, which can bring out prominent socioeconomic performance [1]. Moreover, with the increase in building floors, the high-rise buildings are easy to be affected by external disturbances, which will cause deformation and vibration. This problem will bring huge security risks,therefore the expectation for vibration abatement of high-rise buildings becomes more imperative [2].

For the high-rise buildings, the deformation of the structure is not negligible, and the structure is continuous in physics. Its structure has the characteristics of large span, hence it can be regarded as a kind of flexible structures, which have an infinite dimensionality. For vibration abatement of these systems, the active controller design is more effective than the passive controller design [3]. The systems using passive controllers have the advantages on simple system construction and easy implementation. Nonetheless, when the amplitude of the vibration becomes large, the passive controller cannot effectively suppress the vibration because the control force that this method can provide is limited. On the contrary, the active controllers have the advantages of strong capacity and sufficient input energy. Hence, lots of high-rise buildings adjust active control schemes for decreasing the vibration in serious situations [4], [5]. A couple of active mass driver controllers are installed at the free end of the Canton Tower to mitigate the offset induced by wind [6]. The semi-active tuned mass damper installed on Taipei 101 Tower provides an effective suppressing ability and deals with the off-tuned problem [7]. The active-tuned-mass damper with variable control and sliding mode fuzzy control is designed for protecting a building from the vibration or swing caused by the earthquake [8].

In some cases, a large pendulum which has the huge inertial load can be employed to compensate for the swaying motions of a tall building. In existing research, a tuned mass damper with pendulum control system is put forward for controlling the translation-torsion vibration of tall buildings in the earthquake. In addition, the pendulum mass damper is also designed for reducing the vibration of a long span cablestayed bridge tower. On the basis of the above schemes,engineers in Quancer have presented an innovative vibration abatement idea for the high-rise building systems [9]. In Fig.1,the Quancer platform named Smart Structure shows the controller design method. This platform can be assumed as the coupled flexible-rigid beam system. The rigid beam and the flexible beam have been used to simulate the pendulum and the building, respectively. The tip payload is used to simulate the inertial load. The flexible beam is fixed on the desk.Simultaneously, the rigid beam is mounted to the boundary and the angle are driven by a motor.

In order to decrease the vibration of the high-rise building with more than 14 floors, we need to develop a dynamic model of this system, and this flexible beam has been considered as the EBB (Euler-Bernoulli beam). In this study,we use PDE-ODE (partial differential equation and ordinary differential equation) system to describe the dynamics. With analyzing the system model, it can be found that the displacement and the angle are coupled. The goal of this controlled system is to decrease the vibration by driving the angle. In the past several years, control methods designed for infinite dimensional models caught the attention [10]–[19].Compared with ODE systems, control design for PDE systems is more complicated [20], [21]. In [22], the authors analyze several distributed parameter systems and find that the closedloop behaviors are totally different with different controllers,which illustrate the complexity and difficulty of the control design of infinite dimensional systems.

Fig.1. Laboratory platform.

The distributed controller is a common method in vibration abatement [23]. However, the distributed controller cannot be used in this platform because the sensors and the actuator are limited. In this study, engineers can only measure boundary signals and adjust the boundary control input. Due to this objective situation, authors design the boundary controller with a Lyapunov function. The Lyapunov’s direct method is a common way for designing some controlled systems and analyzing their stability [24]–[32]. In [33], for nonlinear suspension systems, a bioinspired dynamics-based adaptive control is proposed through the Lyapunov framework. In [34],for a rotating flexible spacecraft, authors choose the total energy of the system as a Lyapunov function and prove that the system is stable. In [35], the deleterious vibration source is isolated based on the modeling technique on multiple frequency vibrations and the Lyapunov method.

Boundary control is often applied in actual environments since the actuation is nonintrusive. Meanwhile, it has low cost and simple structure [36]–[39]. For one-link flexible beams,there are many research results [40]–[42]. In [43], authors use two boundary controllers (position and moment actuators) to achieve a prescribed decay rate of the Euler-Bernoulli beam.In [44], authors concentrate on a moving beam system, then they propose a boundary controller for restricting the vibration, while keeping the structure to achieve a desired position. The adaptive control methods are combined with boundary control for dealing with input hysteresis problems in distributed parameter systems [45]. In summary, boundary control of flexible structures has been well studied, and some research results have been obtained for the two-link beam systems. A flexible two-link manipulator is described by PDE and controlled with two DC motors in [46]. In [47], a spacecraft consisting of a long flexible beam (described by PDE) and a rigid body (described by ODE) is regarded as a coupled PDE-ODE system. Then, a robust boundary controller is applied to the PDE subsystem, and a fuzzy control law is used to deal with the ODE subsystem.Compared with the existing work, we focus on an innovative vibration reduction strategy for the high-rise building, and design a boundary control strategy based on the actual device.Note that the desired control goals can be achieved by using fewer actuators.

In this study, we use a flexible-rigid beam structure to simulate high-rise buildings, and investigate a boundary controller to reduce the vibration through theoretical analysis and experimental research. Considering the actual equipment,we can adjust only the torque controller to stabilize the whole system. Differing from the previous works [48], the vibration is quantified as displacement and the rotation is quantified as angle in the system model. The Lyapunov’s direct method has been developed in order to prove that the controlled system is uniformly bounded in the time domain. The availability of our control strategy in different cases is examined by experiments.

The organization of this paper is given. The dynamic analysis of the Smart Structure and lemmas are proposed in Section II. In Section III, we propose a boundary control design and discuss the stability of this system. In Section IV,experiments are implemented to illustrate the accuracy of the model and the actual effect of boundary control law based on the platform. In Section V, the conclusion is given.

II. PROBLEM FORMULATION

Fig.3. Working principle diagram of the Smart Structure.

In the following section, the authors test the practical activity of the controller under different environments. In these cases, we present the platform in five cases, including open loop system, with designed control, with different initial values, with wind disturbance and earthquake disturbance.

B. Experiment Results and Analysis

Case 1: For ensuring safety, we choose the initial state of the system without control in equilibrium.

Figs. 4 and 5 show that the system without control is unstable. We can find that the angle θ (t) increases rapidly. The pendulum fell rapidly in a short time, and its angle exceeded the measuring range. Authors forcibly interrupted the experiment at 0.75 s for protecting the platform. Obviously,this case is not allowed in the actual building, it means a major safety accident.

Fig.4. Case 1: w(L,t).

Case 2: We apply boundary control in the next case (Figs. 6 and 7). k1=0.10, k2=0.10 and α=0.0150. w(L,0)=0.8 cm and θ(0)=10◦. Compared with Case 1, the performance of this control system has been significantly improved. The displacement w (L,t) is adjusted within 7 s. At the same time, θ(t)converges to the neighborhood of 0 within 7 s. After 7 s, the closed-loop system remains stable. At the following experiments,we will alter initial conditions of the system and the external disturbance, to test the robustness of the system.

Fig.6. Case 2: w(L,t).

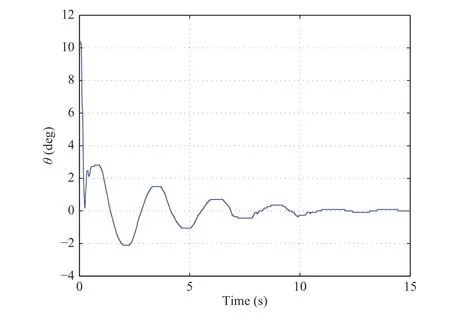
Fig.7. Case 2: θ (t).

Case 3: In Figs. 8 and 9, we change the initial conditions as w(L,0)=1.3 cm and θ(0)=16◦. In this situation, the controlled system is still stable. The boundary displacement w(L,t) and the angle θ (t) can be regulated within 10 s. It shows that the response time of the system will change correspondingly according to different initial conditions. However, the stability will not be affected in this situation.

Fig.8. Case 3: w(L,t).

Fig.9. Case 3: θ (t).

Case 4: In Figs. 10 and 11, we apply a fan to blow the beam for simulating high-rise buildings under the hurricane. The initial conditions are the same as in Figs. 6 and 7. The wind blows from the 5.5 seconds and persists. It is easy to realize that w (L,t) and θ (t) generate offset with blowing. On the other hand, the steady state time has been changed to 15 seconds.This experiment shows that this controller is still effective and it has the ability to counteract the disturbance of the wind.

Case 5: In Figs. 12 and 13, we simulate the situation of high-rise buildings in earthquake by shaking the support plate.The initial conditions are the same as in Figs. 6 and 7. We shake the support plate with a high frequency in the 4.5 to 6 seconds. During this process, both the flexible and the rigid beam undergo continuous vibration. However, both w(L,t)and θ(t) remain within a safe range. After we stop shaking, the displacement and the angle converge to the neighborhood of zero within 10 s. This case shows that the proposed controller can restrain the disturbance of the earthquake.

The control inputs in different situations are shown in Fig.14. In summary, we find that the open-loop system is unstable. In comparison, when we use the proposed controller,the system is stable under different conditions (with different initial values, with wind disturbance and earthquake disturbance). The results show that the boundary controller in this paper achieves the goals in actual experiments.

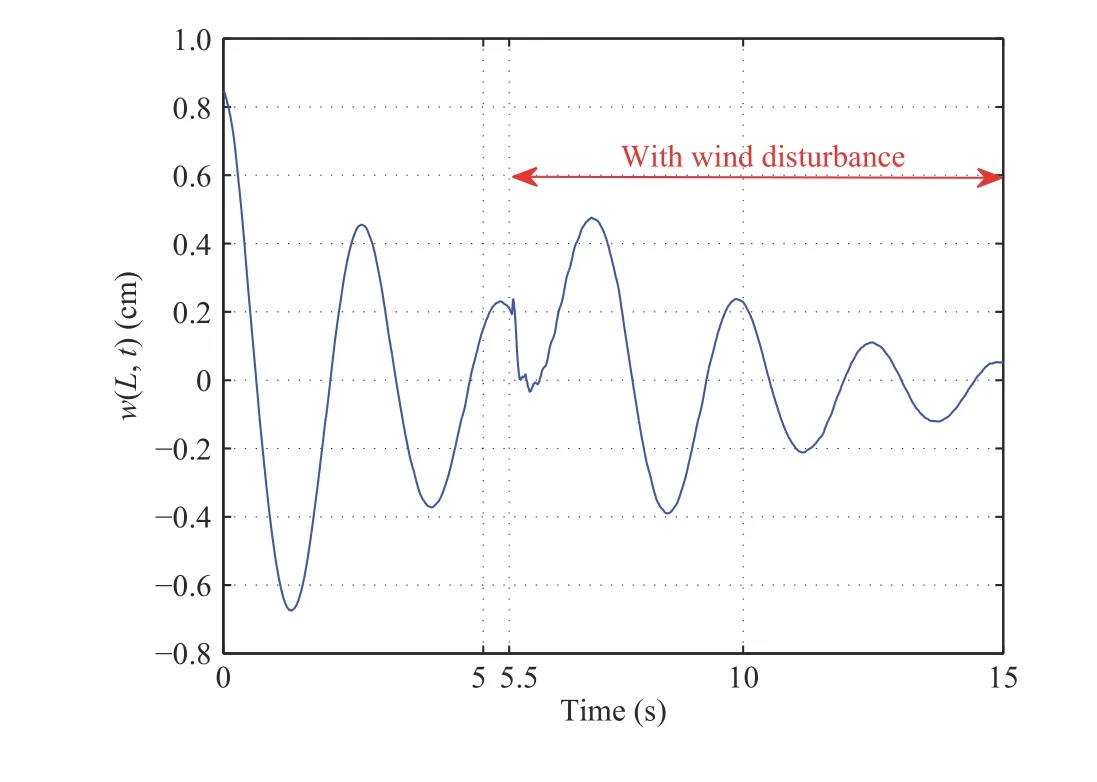
Fig.10. Case 4: w(L,t).

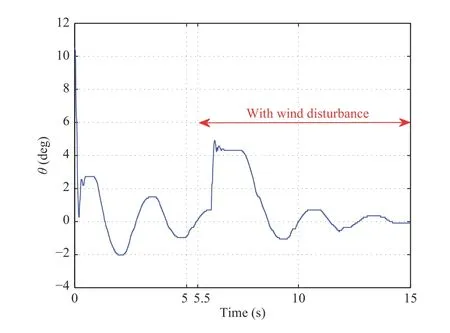
Fig.11. Case 4: θ(t).

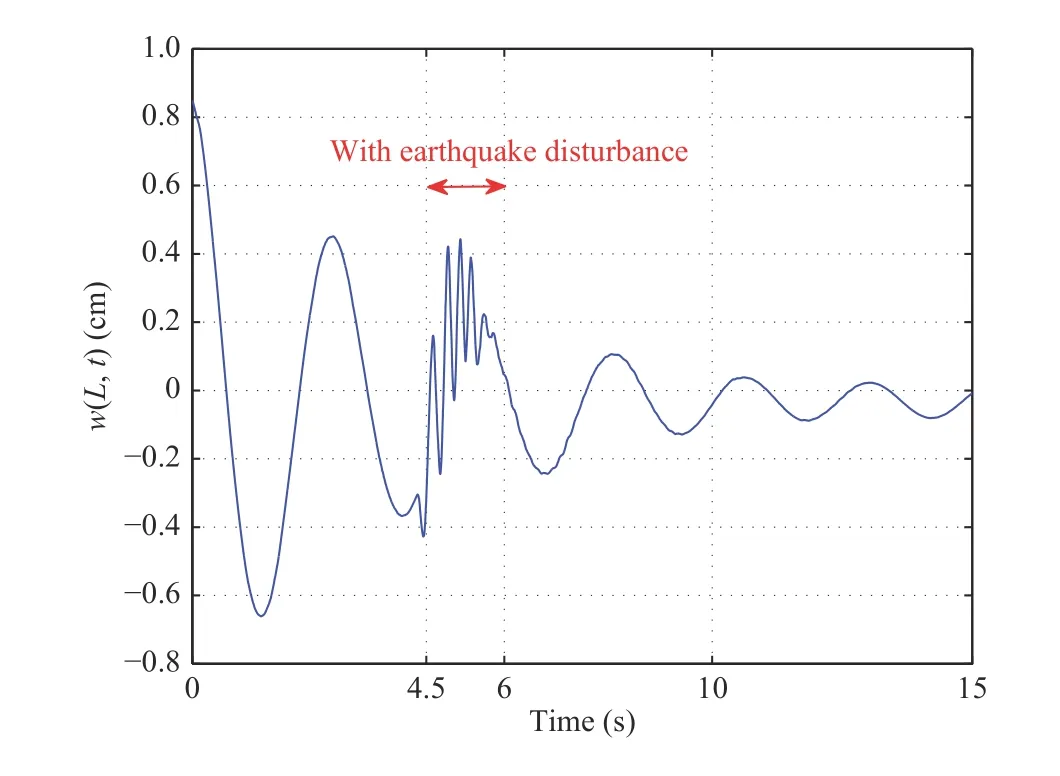
Fig.12. Case 5: w(L,t).

V. CONCLUSION

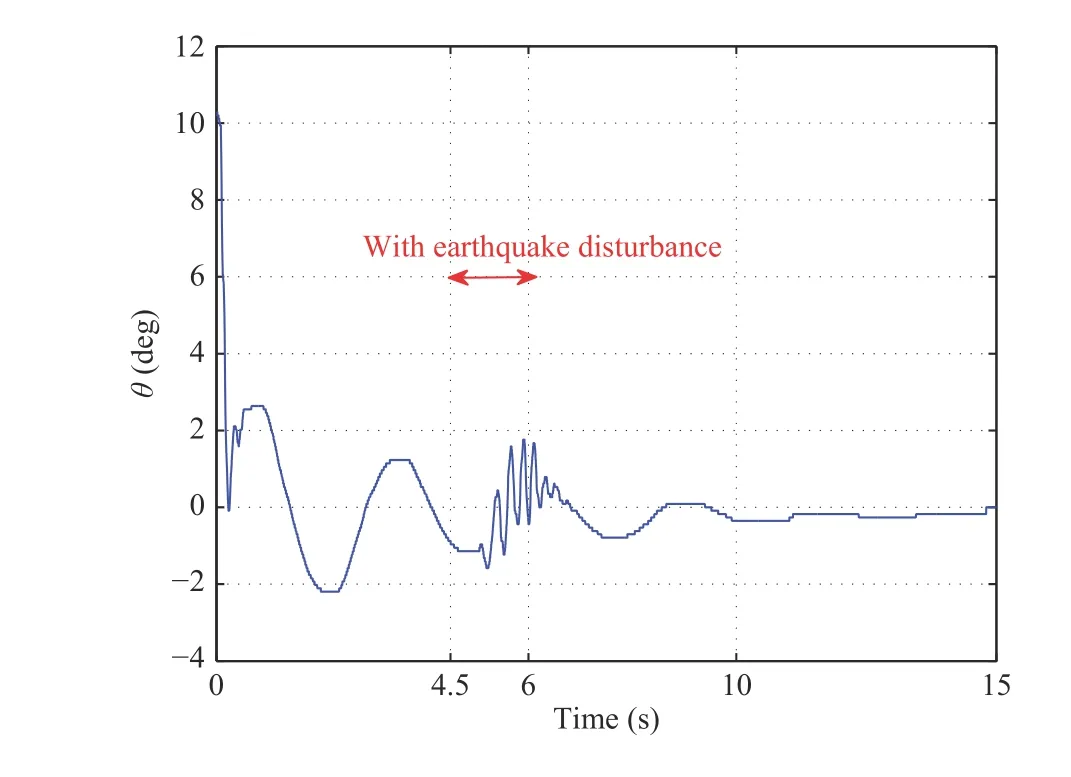
Fig.13. Case 5: θ (t).

Fig.14. Input voltage.

In this research, the system model of a Smart Structure platform has been given for discussing the vibration abatement of high-rise buildings. The model is described by PDE-ODEs and they are derived from the Hamilton’s principle. One boundary control strategy is used in order to reduce the vibration and ensure the stability, simultaneously.The performance of the controller is proved through theoretical analysis. On the basis of the platform, some actual experiments are carried out. Five different situations are tested to discuss the importance of vibration control. Meanwhile, the effectiveness of our method is demonstrated. In the future,input nonlinearities, output constraint and some advanced control methods can be studied [51]–[59]. Meanwhile, we will also analyze the system frequency and simulate the real environment.