Fixed-Time Output Consensus Tracking for High-Order Multi-Agent Systems With Directed Network Topology and Packet Dropout

Junkang Ni, Peng Shi, Fellow, IEEE, Yu Zhao, Member, IEEE, and Zhonghua Wu

Abstract—This paper studies the problem of fixed-time output consensus tracking for high-order multi-agent systems (MASs)with directed network topology with consideration of data packet dropout. First, a predictive compensation based distributed observer is presented to compensate for packet dropout and estimate the leader’s states. Next, stability analysis is conducted to prove fixed time convergence of the developed distributed observer. Then, adaptive fixed-time dynamic surface control is designed to counteract mismatched disturbances introduced by observation error, and stabilize the tracking error system within a fixed time, which overcomes explosion of complexity problem and singularity problem. Finally, simulation results are provided to verify the effectiveness and superiority of the consensus tracking strategy proposed. The contribution of this paper is to provide a fixed-time distributed observer design method for high-order MAS under directed graph subject to packet dropout, and a novel fixed-time control strategy which can handle mismatched disturbances and overcome explosion of complexity and singularity problem.

I. INTRODUCTION

RECENTLY, increasing attention has been given to coordinated control of MAS since the MAS exhibits many useful and important features worthy of research [1]–[5]. As a fundamental behavior of MAS, consensus tracking means all the followers can reach consensus on the leader’s trajectory. There are two kinds of consensus tracking, i.e.,full-state consensus tracking and output consensus tracking.Full-state consensus tracking requires that all the states of each follower track the leader’s trajectory, which is often suitable for first-order and second-order MAS. Output consensus tracking implies that the output of each follower tracks the output of the leader, which is often suitable for high-order MAS. Consensus tracking has been applied in many fields, such as, mobile robots, unmanned aerial vehicles,autonomous underwater vehicles, and microgrids.

In practical MAS, due to oversaturated communication link,channel fading, actuator suspension, noise interference,excessive distance between transmitter and receiver, sensor failure and network attacks, packet dropout is inevitable. Most of the existing consensus tracking protocols rely on reliable information transmission and they may lose effectiveness in the event of packet dropout. Packet dropout changes the communication topology stochastically, introduces consensus tracking error, reduces control performance and even causes instability. Therefore, it is necessary to take packet dropout into account when designing consensus tracking protocol.Recently, fruitful results have been reported on consensus tracking with consideration of packet dropout. References[6]–[8] modeled packet dropout as a Bernoulli distribution stochastic process and used the previous states of its neighbors to construct the current control strategy when packet dropout occurs. In [9]–[14], packet dropout was modeled as timevarying connection strength subject to Bernoulli distribution,i.e., the connection strength will become zero if packet dropout occurs in the communication link. In [15], a stochastically perturbed communication channel was used to describe packet dropout. Based on historical data, the predictive compensation method was presented in [16], [17] to replace missing data when packet dropout occurred. Reference[18] considered deterministic packet dropout and applied switched system with stable and unstable subsystem to develop a zero input packet dropout consensus tracking protocol. Wen et al. [19] treated packet dropout as intermittent communication. In [20], the effect of packet dropout was modeled as a multiply of the transmitted signal and packet dropout rate. In [21], packet dropout was modeled as a Markov chain. These results developed consensus tracking protocols and proved the asymptotical convergence of the presented control strategy using Lyapunov approach,stochastic analysis and stability property of system matrix.However, all these results can only achieve asymptotical consensus tracking, which means that consensus tracking cannot be achieved within finite time.

Consensus time is an important evaluation index of consensus tracking protocol. Fixed-time consensus can achieve consensus tracking within finite time bounded by a constant. Compared with asymptotical consensus tracking,fixed-time consensus tracking shows superiority in consensus time and robustness against uncertainties and disturbances.These remarkable advantages facilitate wide applications of fixed-time consensus tracking approach. Especially for some time-critical tasks, such as power system emergency control,there is an urgent need to develop fixed-time consensus tracking control protocol. In [22], a fixed-time consensus tracking protocol was developed for networked wheel mobile robots under directed graph. Based on addition of a power integrator technique, [23] dealt with fuzzy practical fixed-time consensus of second-order MAS with directed graph. A fixedtime event/self-triggered consensus tracking problem for nonlinear MAS was investigated in [24]–[26]. A fixed-time consensus tracking problem has been studied for second-order MAS under undirected graph [27] and directed graph [28],second-order MAS with cooperative and antagonistic interaction [29], second-order MAS with bounded input uncertainties [30] and external disturbance [31], high-order nonlinear MAS with switched communication graph [32],high-order MAS under directed graph [33], and nonlinear MAS with discontinuous inherent dynamics [34]. Ning and Han [35] was concerned with fixed-time leader-following consensus of nonholonomic chained-form MAS. Huang and Jia [36] reported fixed-time state-feedback and outputfeedback leader-following consensus of nonlinear secondorder MAS. Zhang et al. [37] gave fixed-time formation control approach for networked hypersonic gliding vehicles with directed graph. By means of adding a power integrator technique, an adaptive neural network consensus tracking control protocol was developed in [38] for uncertain nonlinear MAS with output constraint and dead-zone. In [39], fixedtime lag consensus tracking problem was addressed for second-order MAS with input delay. Zuo et al. [40] provided a survey of recent development of fixed-time consensus control. Although great achievements have been made on fixed-time consensus tracking, these previous works assume that the communication link is ideal and each agent can receive all the information transmitted by its neighbors.However, packet dropout is inevitable in practical communication environment and these methods may lose effectiveness if packet dropout occurs.

To the best of our knowledge, no results have reported fixed-time consensus tracking problem of high-order MAS with directed interaction graph and packet dropout. However,this issue is worthy of research. First, due to oversaturated communication link, channel fading, actuator suspension,noise interference, excessive distance between transmitter and receiver, packet disorder and network attack, packet dropout is inevitable. Packet dropout changes the communication topology stochastically, introduces consensus tracking error,reduces control performance and even causes instability. Since packet dropout prevents each agent from obtaining real-time information of its neighbors, it adds difficulty of control strategy design to achieve consensus tracking. Second, since many practical systems have high-order dynamics and a system with high-order dynamics is more general than a system with first-order or second-order dynamics, studying consensus tracking problem for high-order MAS has greater significance than that for first-order or second-order MAS.Third, compared with undirected communication graph,directed communication graph can reduce resource costs and requirement of communication channel, reduce costs for communication infrastructure, strengthen the scalability of the control protocol and enhance the tolerance to failure, delay and interference. However, due to the asymmetry property of digraph, the consensus tracking schemes that rely on symmetry topology cannot be used to achieve consensus tracking for MAS under digraph. Fourth, fixed-time consensus tracking can guarantee all the followers track the leader’s trajectory within bounded time. This facilitates control protocol design to satisfy the demand of some time-critical tasks. Besides, compared with asymptotical consensus tracking, fixed-time consensus tracking has some better performance in terms of convergence rate, convergence accuracy and robustness.

Motivated by the aforementioned discussion, this paper investigates fixed-time consensus tracking problem of highorder MAS under directed interaction graph and packet dropout. The contributions of this paper are:

First, this paper addresses fixed-time consensus tracking problem for high-order MAS under directed interaction graph and packet dropout. This issue is nontrivial since many challenging problems need to be solved; for example, how to compensate for data loss caused by packet dropout, how to design a distributed observer to overcome the difficulty brought by the asymmetrical property of digraph and data loss caused by packet dropout, and how to design a controller that is singularity-free. This paper addresses this important and challenging issue.

Second, a novel fixed-time distributed observer is proposed,which can give an estimation of leader’s states for MAS with directed communication graph and packet dropout. The existing fixed-time distributed observers rely on reliable information transmission and they may lose effectiveness in the event of packet dropout. Determining a method to provide an estimation of leader’s states in the presence of packet dropout is still a challenging issue. Further, the asymmetric property of digraph also adds complexity to distributed observer design and fixed-time stability analysis. Moreover,the nonlinear property of fixed-time distributed observer further increases the difficulty of design and stability analysis.There are no results reporting fixed-time distributed observer for MAS with directed communication topology and packet dropout. This paper presents a novel distributed observer design method to estimate leader’s states under directed communication graph and packet dropout and provides rigorous fixed-time stability proof.

Third, this paper presents a novel fixed-time adaptive dynamic surface controller to stabilize tracking error system.Backstepping method is a good approach to design fixed-time controller for high-order system. However, using backstepping method to design a fixed-time controller for high-order system has two problems, i.e., explosion of complexity and singularity problems. The explosion of complexity problem results in great difficulty in deriving and calculating control law, which increases computation burden and implementation difficulty tremendously. The existence of singularity problem reduces convergence accuracy and degrades control performance. Furthermore, the distributed observation error caused by packet dropout also introduces unknown mismatched disturbances to system dynamics. Since the upper bound of mismatched disturbance is unknown, it is difficult to design disturbance observer to estimate and compensate for unknown disturbance or develop robust term to eliminate the effect of the disturbance. In this paper, we present a novel fixed-time adaptive dynamic surface controller, which can overcome explosion of complexity and singularity problem and eliminate the effect of mismatched disturbances.

Notation: sig(x)α=|x|αsign(x) , where x ∈R, α ≥0 and sign is standard sign function. ‖ x‖frepresents f-norm of the vector x. Other notations used in this paper are standard, and would be defined otherwise.

II. PROBLEM FORMULATIONS AND PRELIMINARIES

A. Graph Theory

Since packet dropout is inevitable in a networked communication environment, we consider packet dropout when designing consensus tracking control protocol in this paper. Taking stochastic feature of packet dropout into account, we model packet dropouts on each communication link as an i.i.d Bernoulli variable. For communication link(vi,vj), define the Bernoulli variable as γij(t)∈{0,1}. γij(t)=0 indicates that the information is transmitted successfully from node i to node j at time t. γij(t)=1 indicates that the information packet is lost in the communication link (vi,vj) at time t. The Bernoulli variable γij(t) satisfies P r{γij(t)=1}= γ¯ij,Pr{γij(t)=0}=1−γ¯ijand γ¯ijdenotes the packet loss rate which can be estimated through experimental measurement[42].

We made the following assumptions with regard to the studied MAS:

Assumption 1: Graph G (A) is a directed spanning tree.

Assumption 2: The leader’s control input is bounded by a constant λ which is available to all the followers.

Assumption 3: The maximum number of consecutive packet dropout is φ.

Remark 1: The reasonability of Assumptions 1 and 2 has been explained in [27] and [39]. With the development of communication technology, the packet dropout rate can be reduced significantly. Since consecutive packet dropout is an independent event and the packet dropout rate can be made significantly small, the probability of losing more than φ consecutive packets is very small. As shown in [43], the event that the number of consecutive packet dropout exceeds a certain threshold can be treated as an impossible event.Moreover, if the number of consecutive packets dropout is unbounded, the desired property and even stability of MAS cannot be guaranteed, which is not allowed in practical networked control. In fact, if the number of consecutive packets dropout is too large, the designer should focus on control of network to improve communication quality and reduce packet dropout. Moreover, the maximum number of consecutive packets dropout is an evaluation index of communication network reliability which can be obtained by experiments. Therefore, Assumption 3 is reasonable.

Practical fixed-time output consensus tracking means that the output of the studied MAS satisfies limt→T(x(0))|yi(t)−y0(t)|≤ϵ with i=1,...,N and desired accuracy ϵ>0, while the boundedness of the other states can be guaranteed and the settling time function T(x(0)) is bounded by a constant Tmaxirrespective of initial value x(0).

The problem studied in this article is formulated as designing an appropriate consensus tracking control protocol for the MAS (1) and (2) with consideration of finite consecutive packets dropout such that practical fixed-time output consensus tracking of the MAS (1) and (2) can be achieved.

Remark 2: Practical fixed-time convergence results have been reported in many references and applied in many fields.In [44], a practical fixed-time stable guidance law was presented to achieve an autonomous landing on Mars. In [45],a practical fixed-time attitude control was developed for a flexible spacecraft with consideration of external disturbances,actuator faults and coupling effect of flexible modes. In [46], a practical nonsingular fixed-time fuzzy control was designed for uncertain robotic systems with user defined performance boundary constraints.

Remark 3: Output consensus tracking problem has been studied for many high-order MASs. The work in [47] studied output consensus tracking problem of heterogeneous linear MAS under switched topology. In [48], fault-tolerant output consensus tracking problem of uncertain stochastic MAS subjected to actuator faults and input saturation was investigated. However, all these results can only achieve asymptotical output consensus tracking. This paper develops a consensus tracking protocol which can achieve fixed-time output consensus tracking.

C. Preliminaries

Lemma 2 [49]: For ψ1,...,ψN≥0, β >1, we have

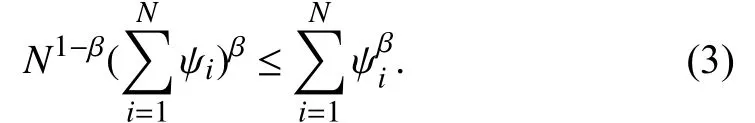
Lemma 3 [49]: For ψ1,...,ψN≥0, 0 <β<1, we have

ψ ∈RNf >g>0

Lemma 4 [49]: For any and , one has

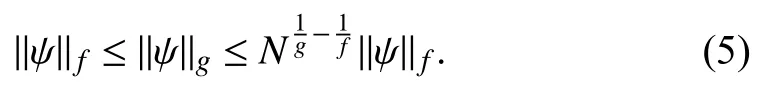
Lemma 5 [50]: For ψ ∈R and ρ >0, one has

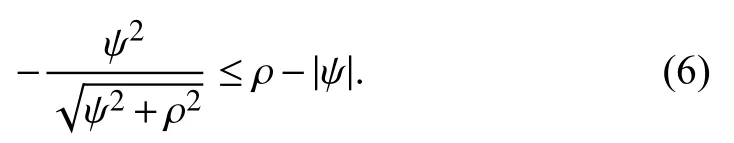
Lemma 6 [51]: For any z ∈R , we have 0 ≤|z|−ztanh(z/ϵ)≤ρϵ with ϵ ≪1 and ρ =0.2785.

III. MAIN RESULTS

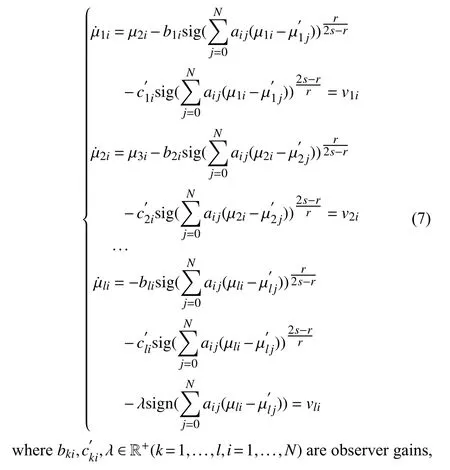
Remark 4: The schemes presented in [6], [7] only consider single packet dropout. In fact, it is likely that consecutive packet dropout occurs in networked communication environment and consecutive packets dropout does more harm to the consensus performance of MAS than single packet dropout.These schemes may lose effectiveness in the event of consecutive packet dropout. Besides, in [7], it is assumed that packet dropout is homogeneous, that is, the packet dropout rate is the same for each communication link. This assumption is very restrictive since it ignores the difference between each communication link. In this paper, we consider consecutive and heterogeneous packet dropout, which is closer to practical packet dropout that occurs in network communication environment.

Remark 5: In [6]–[8], the previous state value received from its neighbors is used to replace the current state value of its neighbors when packet dropout occurs. In [9]–[14], [18], and[19], the current states of its neighbors are taken to be zero when packet dropout occurs. In [15] and [20], a multiply of the neighbor’s states and probability of successful information transmission is used to design controller, which is similar to the method adopted in [9]–[14], [18], and [19]. None of these methods give a reasonable states of its neighbors when packet dropout occurs, which may degrade system performance and even lead to system instability. In this paper, we develop a predictive based compensation to replace the current state value of its neighbors when packet dropout occurs. The predictive algorithm is based on historical states, which can reflect the evolution dynamics of neighbor’s states and is more reasonable than the methods presented in [6]–[8] and the methods presented in [9]–[15], [18]–[20].

Remark 6: Due to the stochastic property of packet dropout,the neighboring agent cannot determine whether the information transmission will be successful before it transmits its distributed observer’s states. Once packet dropout occurs and if there is no predicted value available, the distributed observer can only use the unreasonable distributed observer’s states of its neighbors to estimate the leader’s states, which will result in incorrect estimation of the leader’s states.Therefore, prediction of the distributed observer’s states is necessary and required during the whole process.

Remark 7: Since all the predictive values of the distributed observer’s states of an agent are put into one data packet, the number of the transmitted data packets will not increase but the size of data packet will increase, which may increase packet dropout rate. As discussed in Remark 6, this is the cost of improving system performance and the accuracy of the leader’s states estimation. There are three ways to deal with the possible effect of the increment of packet dropout rate caused by the increment of packet size and achieve sufficiently high consensus control performance. First, one can evaluate the effect of packet size on the packet dropout rate and determine an appropriate packet size. Second, one can design an appropriate robust term to eliminate the disturbance caused by packet dropout. Third, one can improve communication environment and communication technology.

The error due to packet dropout can be written as

We can select model predictive method, neural network,time series method, grey prediction, support vector machine,chaos algorithm as a prediction algorithm. Due to short-term prediction, we can guarantee sufficiently high prediction accuracy. Therefore, the error is bounded, i.e., there exists ξkij∈R+such that |ekij|≤ξkij. The prediction can be made at the sending end. An agent can pack its current states,prediction of its future states for every possible packet dropout together with time stamp into one data packet and send it to its neighbors. When an agent receives the data packet from its neighbors, it will use the current states of its neighbors to construct a distributed observer and store the predicted states of its neighbors in a buffer for any possible packet dropout in future information exchange. If an agent does not receive a data packet within a certain transmission time, the agent will assume that packet dropout has occurred in the communication link and the selector will choose the correct predicted states from the buffer according to time stamp and send it to the distributed observer. In this way, the predictor based distributed observer can compensate for packet dropout and give an estimation of the leader’s states. Further, with the predictive cloud compensation scheme [43], the computational burden of predictive algorithm can be reduced and computational efficiency can be improved.

where dki=−µ˙ki+µ(k+1)ifor k=1,...,l−1 and dli=−µ˙li.From stability analysis in Appendix, we have that dkiis bounded, i.e., a positive constant Dkican be found such that|dki|≤Dki.

Remark 8: Matched disturbances are the ones that appear in the same channel as the control input, while mismatched disturbances are the ones that appear in different channels from the control input. For example, in (11), since the disturbance dliand control input uiappear simultaneously in the last channel, i.e., eeli, we call the disturbance dlias matched disturbance. Since the disturbances dji(j=1,2,...,l−1) appear in channels eeji( j=1,2,...,l−1) but no control input appears in these channels, we call the disturbances dji(j=1,2,...,l−1) as mismatched ones.

Next, we will develop a fixed-time tracking controller to achieve stabilization of error dynamics (11).

Step 1: The first dynamics of tracking error system can be expressed as inequality whose computation complexity grows significantly with the increase of system dimension and the scale of the MAS. Heavy computation burden prevents their applications to large scale and high-dimensional MAS. Besides, high computational complexity prevents real-time and online implementation of these schemes. Second, the schemes presented in [6], [7], [9], [11], [13], [15], [17], [19] require global information, i.e., the Laplacian matrix or the eigenvalue of Laplacian matrix, to determine design parameters. This means that these schemes are not fully distributed. Third, the algorithms presented in [6], [9], [10], [13] can only be applied to MAS under undirected communication graph. Directed graph has been applied in wider fields while it also poses a great challenge to consensus tracking scheme design due to its asymmetry property. Fourth, the methods presented in [9],[10], [17] are only suitable for low-order MAS. Many MASs have high-order dynamics and many challenging issues need to be addressed to extend these methods to high-order MAS,such as singularity problem and computational complexity problem. Fifth, these approaches can only achieve asymptotical consensus. Since fixed-time consensus can achieve consensus within a fixed time and has higher convergence accuracy and stronger robustness against uncertainties and disturbances, it is desirable to design a consensus tracking strategy to achieve fixed-time consensus. In this paper, we present a novel fixed-time consensus tracking algorithm for high-order MAS with directed graph and packet dropout,which is fully distributed and scalable. The consensus tracking scheme presented in this paper overcomes these deficiencies.

Remark 14: In [22]–[40], the consensus tracking strategy is developed and fixed-time stability analysis is conducted based on the assumption that the communication channel is ideal and perfect, i.e., real-time reliable information exchange can be guaranteed all the time. However, packet dropout is inevitable in networked communication environment. Without real-time reliable information exchange, these consensus tracking strategies may lose effectiveness, and the followers’states may deviate from the leader’s trajectory and even lose stability. The existence of packet dropout poses great challenges for fixed-time consensus tracking protocol design since real-time information may be unavailable for control protocol updates and fixed-time convergence of the designed control protocol cannot be guaranteed if information exchange is interrupted or destroyed. In this paper, we address this challenging issue by developing a novel distributed observer based consensus tracking strategy to achieve fixed-time consensus tracking of MAS in the presence of packet dropout.

IV. SIMULATION RESULTS

In this section, we apply the proposed consensus tracking scheme to networked single-link manipulators and their dynamics satisfy

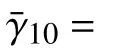
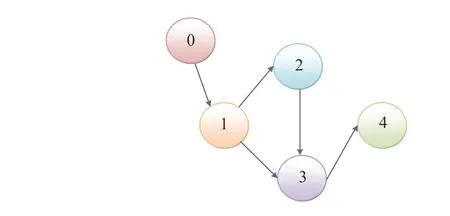
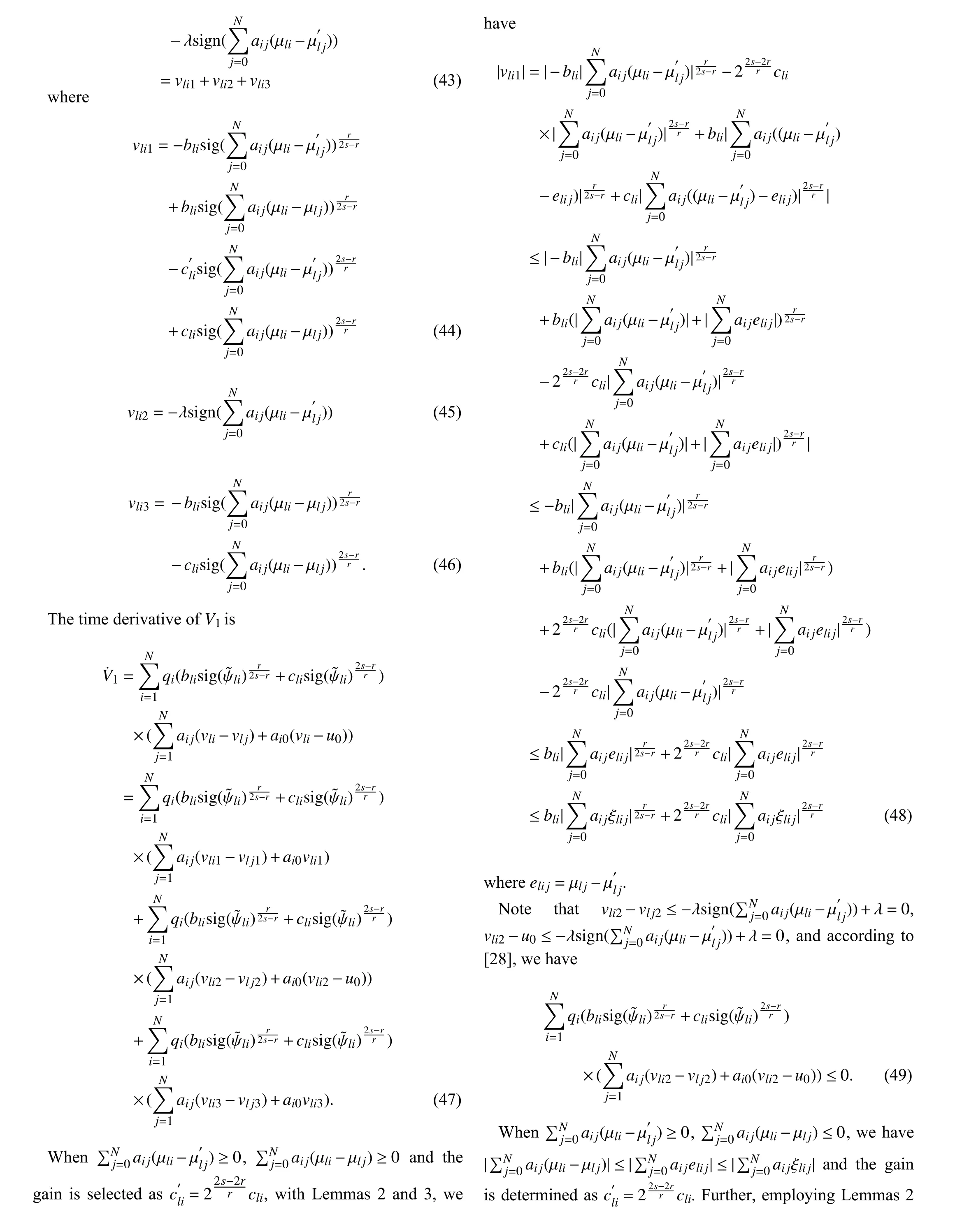
Fig.1. The interaction graph.

Finally, a comparative study is conducted to show the advantage of the proposed consensus tracking protocol. The consensus scheme developed in [16] is used to conduct a comparison. For fair comparison, the parameters that both controllers share and the simulation condition are selected to be the same. The response of the MAS states under the scheme developed in [16] is demonstrated in Fig.6, from which we can see that the scheme developed in [16] cannot force the followers’ states to track the leader’s trajectory well within 20 s and obvious tracking error can be observed. Note that the existence of packet dropout introduces mismatched disturbances in tracking error dynamics. It can be seen that the proposed consensus scheme has an advantage over the scheme developed in [16] in convergence time, convergence accuracy and robustness against disturbances.

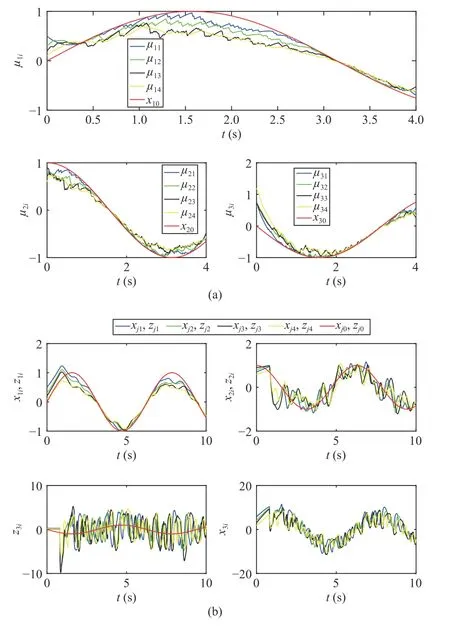
Fig.3. Results of the consensus tracking scheme using zero state to replace the lost packet (a) distributed observer states µ1i, µ2i, µ3i (b) MAS states x1i,z1i , x2i,z2i and x3i,z3i.

V. CONCLUSION

In this paper, a novel fixed-time output consensus tracking control strategy has been proposed for high-order MAS under directed graph in the presence of packet dropout. A predictive compensation based distributed observer has been proposed to deal with packet dropout and achieve fixed-time estimation of leader’s states. Mathematical proof has shown that the proposed distributed observer has the fixed-time convergence property. Then, an adaptive fixed-time dynamic surface control has been proposed to eliminate the effect of mismatched disturbance, overcome explosion of complexity and singularity problem, and achieve fixed-time stabilization of the tracking error system. Simulation results have verified the effectiveness and superiority of the proposed control strategy. Event-triggered mechanism provides a good way to deal with communication constraints and may reduce packet dropout rate. Many event-triggered control schemes have been developed, for example see [57]–[59]. In future works, we will combine the proposed consensus protocol with eventtriggered mechanism. Besides, our future work also includes human-in-loop consensus [60] and fault-tolerant consensus[61].

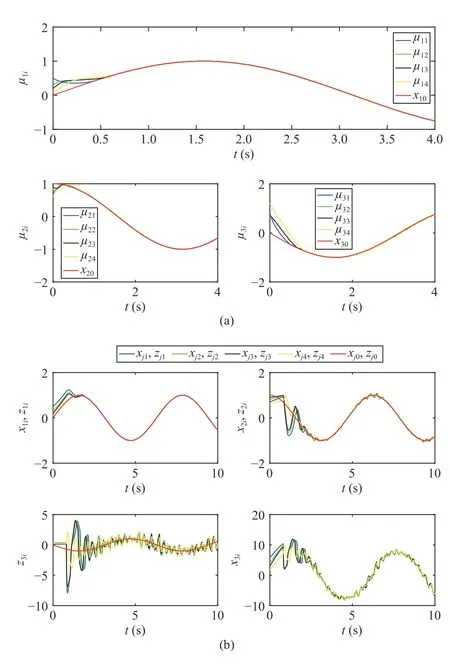
Fig.4. Results of the consensus tracking scheme using hold strategy to tackle packet dropout (a) distributed observer states µ1i, µ2i, µ3i (b) MAS states x1i,z1i , x2i,z2i and x3i,z3i.

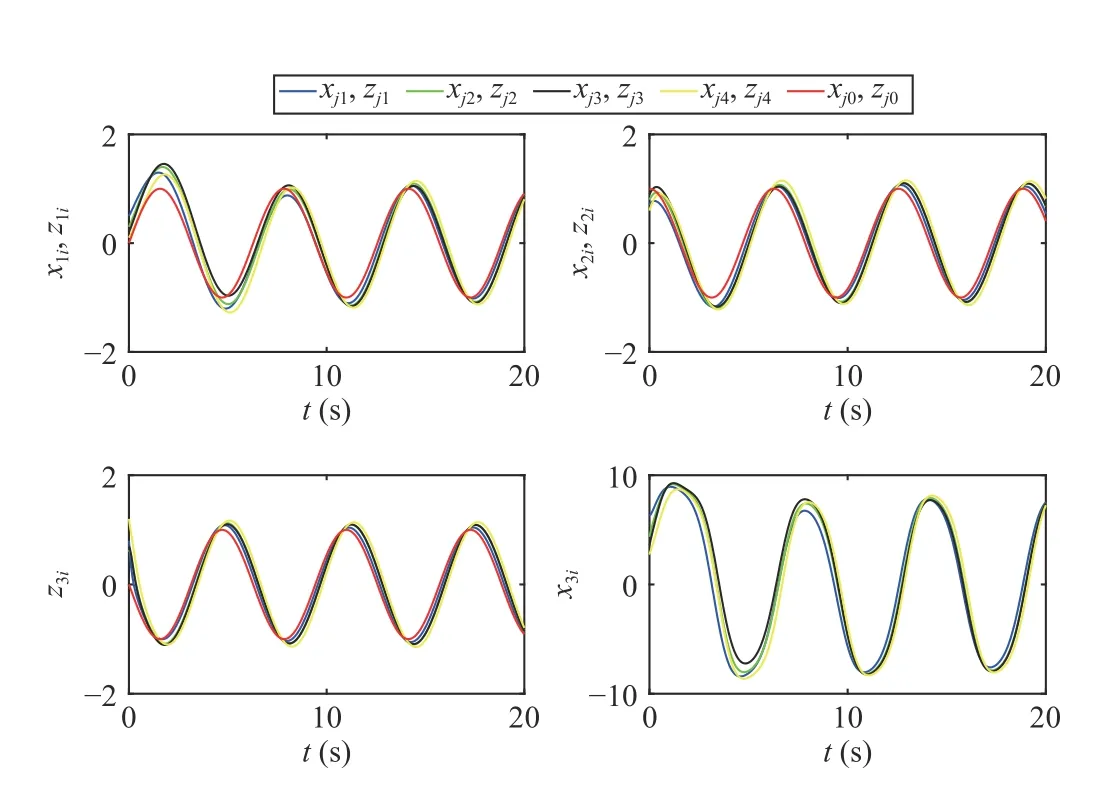
Fig.6. Time evolution of MAS states z1i, z2i, z3i, and x3i under the consensus scheme presented in [16].

APPENDIX

PROOF OF THEOREM 1

Choose a Lyapunov function shown below:

Fig.5. Results of the presented predictive compensation based consensus tracking scheme with step size 0.0001 (a) distributed observer states µ1i, µ2i,µ3i (b) MAS states x1i,z1i , x2i,z2i and x3i,z3i.

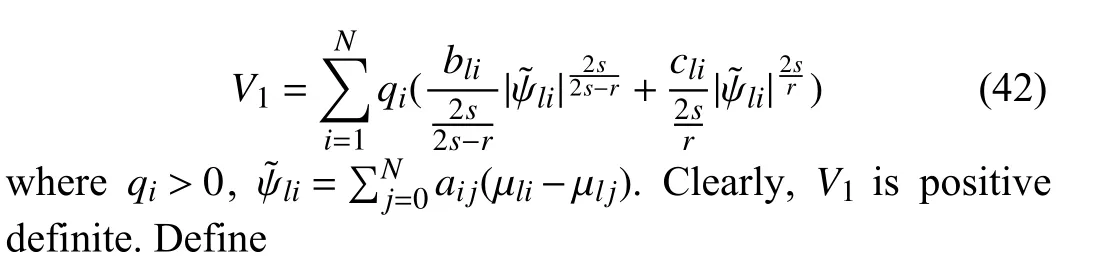
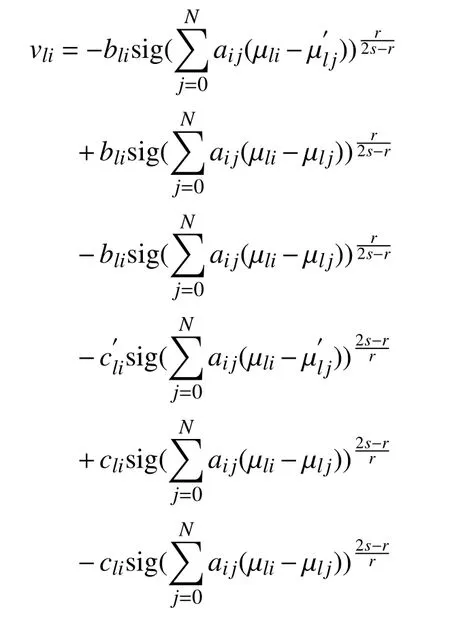
Remark 15: The Lyapunov functions (42) and (78) are designed to analyze the fixed-time stability of the proposed distributed observer. Since qi>0 , bli>0 , cli>0 , b(l−1)i>0,c(l−1)i>0, s>r>0, the Lyapunov functions (42) and (78) are guaranteed to be greater than or equal to zero.