Dynamic Evaluation Strategies for Multiple Aircrafts Formation Using Collision and Matching Probabilities
2021-04-13HongboZhaoYongmingWenSentangWuandJiaDeng
Hongbo Zhao, Yongming Wen, Sentang Wu, and Jia Deng
Abstract—Configuration evaluation is a key technology to be considered in the design of multiple aircrafts formation (MAF)configurations with high dynamic properties in engineering applications. This paper deduces the relationship between relative velocity, dynamic safety distance and dynamic adjacent distance of formation members, then divides the formation states into collision-state and matching-state. Meanwhile, probability models are constructed based on the binary normal distribution of relative distance and relative velocity. Moreover, configuration evaluation strategies are studied by quantitatively analyzing the denseness and the basic capabilities according to the MAF collision-state probability and the MAF matching-state probability, respectively. The scale of MAF is grouped into 5 levels, and previous lattice-type structures are extended into four degrees by taking the relative velocities into account to instruct the configuration design under complex task conditions. Finally,hardware-in-loop (HIL) simulation and outfield flight test results are presented to verify the feasibility of these evaluation strategies.
I. INTRODUCTION
AT present, there are many applications for multiple aircrafts formation (MAF) systems. For example, MAF can improve comprehensive combat effectiveness significantly by carrying out tasks cooperatively. The configuration evaluation of MAF plays an important role in cooperative task execution [1]–[5]. Many efforts have been devoted towards the development of control methods for MAF, such as the leader-follower method [6]–[10], the virtual leader/virtual structure method [11], [12], the behavior-based method[13]–[15], consensus control [16]–[20] and neural network control [21], [22]. Towards realizing an actual MAF system,numerous interesting results about reducing the communication burden are proposed in [23]–[26]. However, few studies have paid attention to the configuration evaluation of the MAF system.
Many studies have used qualitative descriptions, such as“large-scale”, “complex formation”, “close formation”, and“multilayer formation”, to represent the tightness and scale of the formation configuration. For example, a new formation framework of “large-scale” intelligent autonomous vehicles was developed in [27], which can realize “complex formations” while reducing data exchange. A relative positioning solution for unmanned aerial vehicle (UAV)rendezvous was proposed in [28] and the “close formation”flight had been verified in multiple flight tests. A multilayer formation control problem was defined in [29], in which the agents can receive and transmit information among the layers.Previous studies only described the configuration denseness qualitatively rather than quantitatively. In order to give efficient guidance for the tightness and scale design of MAF,we classify the denseness of MAF configuration quantitatively based on the MAF collision-state probability model.
The basic capability of the configuration, i.e., the formation forming and holding ability, is constrained by the MAF members’ maneuverability, the sensor measurement and control accuracy, the network service quality, the task environment, and the denseness and scale of configuration in engineering applications. There was almost no quantitative analysis of them. For example, the formation control problem of multiple quadrotors tasked to achieve aggressive trajectory tracking with prescribed formation patterns was of concern in[30]. In [31], the authors analyzed the formation’s stability and solved the decentralized multivehicle formation control problem. The authors in [32] used Dudek’s taxonomy to evaluate the performance of the autonomous UAV group cooperating in mission execution. A taxonomy was presented to classify the multi-agent systems according to communication, computation and other capabilities in [33]. Most studies provided the qualitative evaluation of the configuration’s basic capabilities, but it is difficult for designers to optimize the formation’s properties to maximize the efficiency-cost ratio in different conditions. Therefore, we evaluate the basic capability of MAF configuration quantitatively according to the MAF matching-state probability model.
Moreover, MAF’s lattice-type structure is an important indicator that can reflect basic capabilities. The more rigid the lattice-type structure, the stronger the basic capabilities. Two lattice-type structures called α-lattice and quasi α-lattice were presented in [34], which only require the distance between formation members to be equal to or approximately equal to the fixed pre-set distance. However, the relative distance is always fluctuating near the pre-set distance; the MAF members are not necessarily isomorphic, thus the pre-set distances between two adjacent members are not always the same. In addition, the α-lattice, quasi α-lattice, and quasi σ-adjacent configuration designed in [1] were all defined according to the relative distance between two members in the formation but the velocity maintaining capability of MAF was not taken into consideration, thereby leading to a lack of completeness. Therefore, the other two lattice-type structures (the σ-adjacent configuration and the quasi σ-adjacent configuration) are complemented in this paper by considering relative velocity to reflect the dynamic properties of the formation configuration.
Interesting results on real-time experimental evaluation of formation control methods have also been reported. Both numerical simulations and field tests with a flock of five quadcopter drones were presented in [35], showing that the proposed flocking algorithm performs well in both the convergence rate and its ability to track the desired path. A real-time experiment was implemented using a team of ground mobile robots in [36], and the experimental formation tracking error and the trajectory illustrated the effectiveness of the proposed methods. In [19], four iRobot Create robots were used in the experiment, and the results showed that the robots’linear and angular velocities are reduced to zero while achieving the desired formation and heading consensus. Most real-time experiments are based on low-speed vehicles such as ground robots and quadcopter drones, and evaluation strategies are based on static criticism. To the best of our knowledge, there are limited experimental results on the evaluation of formation design and containment of cooperative aircraft with high velocity and high dynamic. In order to ensure reliability and safety of high dynamics multiagent systems in the outfield work, the development of dynamic configuration evaluation strategy is of critical necessity.
In a recent paper [37], a formation generation method was proposed, and an actual outfield experiment was carried out with six UAVs. In addition, outfield flight experiments were carried out to verify the effectiveness of the proposed control method in [38] and [39]. In [38], the result curves of two aircrafts’ flight paths, velocity, and relative distance showed that the formation collisions and the chain effect are avoided effectively. In this paper, the results of [37]–[39] are significantly extended by considering configuration evaluation strategies for a team of cooperative fixed-wing unmanned aircraft.
Motivated by the above discussion, this study focuses on quantitative configuration evaluation strategies for MAF systems based on collision probability and matching probability. The main contributions and innovations are summarized as follows.
1) A novel evaluation method for highly dynamic MAF systems is discussed in this paper, which considers both the relative distance and relative velocity between formation members. In order to quantitatively describe the evaluation indicators, the MAF matching-state probability model and the collision-state probability model are constructed based on Reynolds three criterions [40].
2) The denseness (including the tightness and the scale) of the MAF configuration is one of the evaluation objects. It is evaluated quantitatively and explicitly according to the MAF collision-state probability for the first time in this paper. The MAF tightness and scale are classified into 3 and 5 levels,respectively.
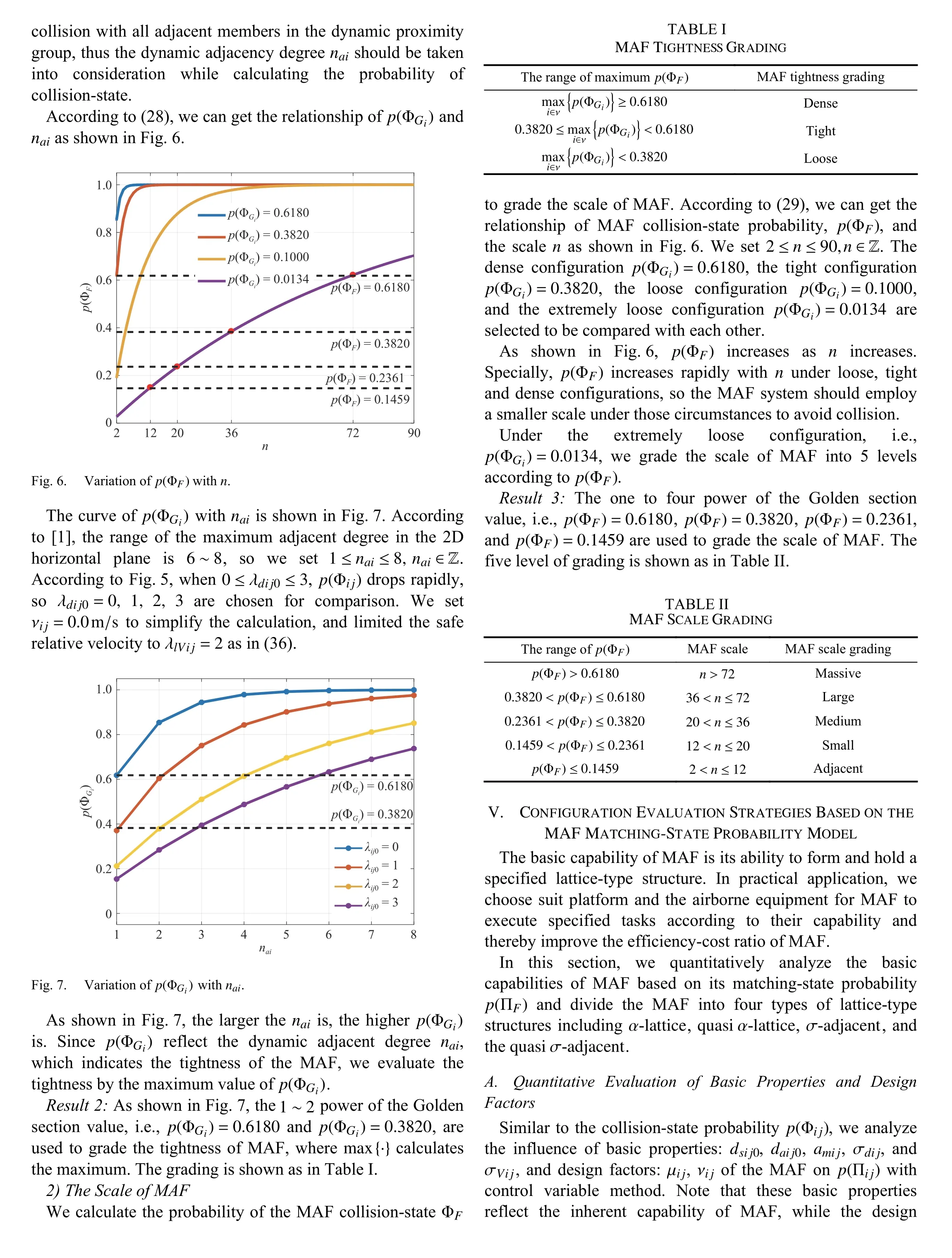
3) The basic capabilities (the ability to form and hold a specified lattice-type structure) of the MAF configuration is another evaluation subject. It is evaluated quantitatively and explicitly according to the MAF matching-state probability for the first time in this paper. A more complete lattice-type structure classification is presented in this paper. Accordingly,four levels of MAF basic capabilities are graded.
4) Most studies involving MAF focuses on the theoretical analysis of the control approaches, whereas the evaluation technology proposed in this paper is motivated by engineering applications and has been verified by both hardware-in-loop(HIL) simulations and outfield flight tests.
The rest of this paper is organized as follows. In Section II,the background, basic knowledge, symbol definitions, and assumptions of the MAF are given. In Section III, the division of MAF collision-state and matching-state are presented,along with their probability models. Configuration evaluation strategies based on the MAF collision-state probability model and MAF matching state probability model are given in Sections IV and V, respectively. In Section VI, HIL simulation and outfield experiment results are presented to verify the feasibility of these evaluation methods. Finally,concluding remarks are given in Section VII.
II. PRELIMINARIES
A. Background and Basic Knowledge

more complicated and closer to engineering applications than that of MAF in 3D space. Therefore, based on the above analysis, the configuration evaluation of the flat MAF in a 2D horizontal plane will be studied in this paper.
B. The Distribution of the Relative Vector
Lemma 1 (Wu [1]): Suppose that the distance dij(t) is an ergodic stochastic process, according to the central limit theorem, under the combined effects of various indistinctive random factors, and dij(t) approximately obeys the normal distribution


C. Assumptions [38]
1) Members of MAF can obtain information about local absolute positions and velocities through the navigation system in real-time.
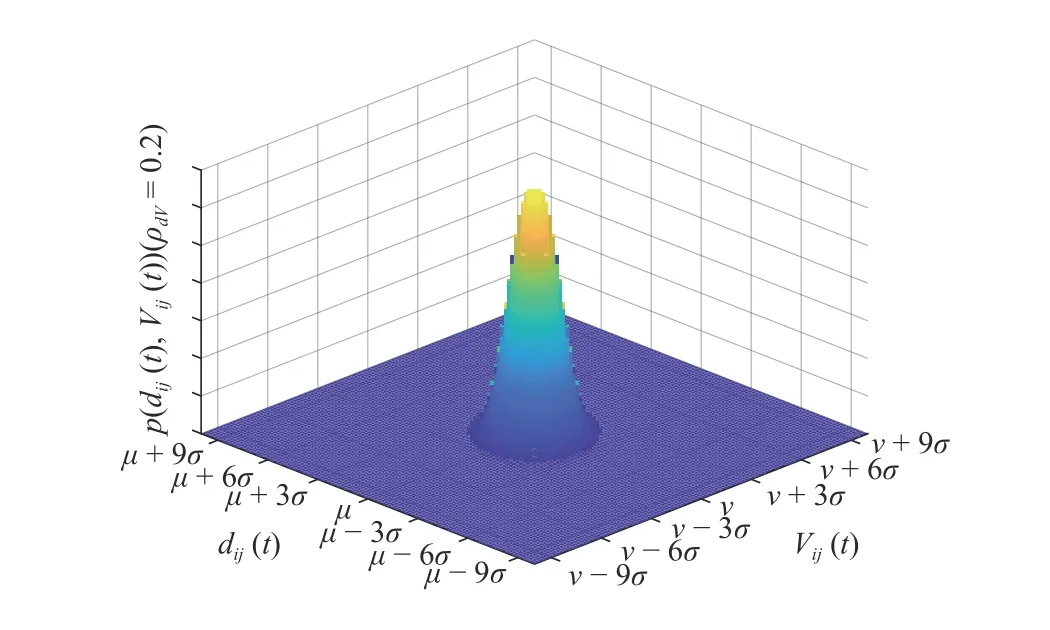
Fig.1. Probability density surface of Dij(t).
2) The communication network of MAF only needs to be connected in the proximity groups through the one-hop or multi-hop pattern.
III. DYNAMIC MAF STATES PROBABILITY MODELING
Based on the Reynolds three criterions [40] (speed matching criterion, mutual attraction criterion, and mutual exclusion criterion), the matching-state and the collision-state probability models are constructed in this section to indicate the dynamic mutual exclusion and speed matching processes,respectively. With these probability models, we can quantitatively describe the evaluation indicators in the following sections.
In this section, the dynamic safety distance and dynamic adjacent distance are first introduced to divide the state of two flight members. After that, the states of two members are extended to the states of the dynamic proximity groups and then coming to the states of MAF.
A. Dynamic Safety Distance
When the relative velocity is 0, the static safety distance is dsij0, which is the sum of the sensor error and control error,the maneuverability, the network induced noises, and the task environment disturbances. When the relative distance is less than the static safety distance, there will be a risk of collision,and the aircraft need to take maneuver immediately to avoid collision [1].
When there is a nonzero relative velocity, the static safety distance turns to be the dynamic safety distance dsij(t). If the relative velocity is greater than 0, i.e., the two formation members fly far away from each other, the safe distance is dsij0; if the relative velocity is less than 0, i.e., the two formation members fly towards each other, extra distance is required for acceleration. Therefore, the dynamic safe distance will increase correspondingly. The relationship between dsij(t)and relative velocity is as follows.
According to the static safety distance dsij0, if
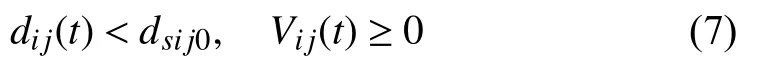
then a collision occurs between xiand xj.
When Vlsij≤Vij(t)<0, and there is a relative acceleration amij>0 between xiand xj, Vij(t) is made to accelerate to 0 as quickly as possible to avoid collision. amijis the maximum relative acceleration, which is determined by the maneuverability of the aircraft. The collision condition between xiand xjis
dij(t)−Vij2(t)/(2amij) where Vlsijis the minimum safe relative velocity, which is determined by the static safety distance, the maximum relative acceleration, and the static adjacent distance. The static adjacent distance daij0is the maximum distance required for communication between xiand xj, and satisfies daij0≥dsij0.When dij(t) Considering the situation that the two flight members fly towards each other with the adjacent distance as the relative distance, they should make full use of their maneuverability to decelerate, then by substituting dij(t)=daij0into (8), the minimum relative velocity they can tolerant is Due to the limitation of daij0, when Vij(t) According to (7), (8), and (10), we get the relationship of dsij(t) and Vij(t) In summary, the collision condition between xiand xjis The relationship curve of the dynamic safety distance is shown as in Fig.2, i.e., the dividing curve of the green region and red region. Fig.2. Relationship of relative distance and relative velocity. Allow the static adjacent distance to be daij0. Taking relative velocity into consideration, the static adjacent distance turns into the dynamic adjacent distance. If it satisfies xiand xjdo not need to communicate with each other, and they are in a state of mutual isolation. When 0 where Vlaijis the maximum adjacent relative velocity. By substituting dij(t)=dsij0into (14), we can get When Vij(t)>Vlaijand dij(t) is larger than the static safe distance dsij0, then xiand xjdo not need to communicate, i.e., According to (13), (14), and (16), we can get the relationship of the adjacent distance daij(t) and relative velocity Vij(t) In summary, when xiand xjdo not need to communicate with each other, and they are in a state of mutual isolation. Thus, the network flow pressure can be reduced, and the MAF can use the limited network resources among the members in the dynamic proximity groups to improve the network service quality,which is conducive to the safety, stability, and efficiency of MAF. The relationship of relative distance and relative velocity is illustrated in Fig.2, where Ωijdenotes the relationship plane.The dividing curve of the green region and the red region is the safety distance in (11). The dividing curve of the green region and the blue region is the adjacent distance in (17). Definition 1 (Collision-State): In the relative distance and relative velocity relationship plane shown in Fig.2, the area constrained by (12), i.e., the red region Ψij is defined as the collision-area. xiand xjare in the collisionstate when the relative vector Dij(t) is in the collision-area Φij. According to (6), (11), and (19) we can get collision probability p(Φij) of xiand xjas follows: where P{·} denotes the probability. τ and ω are the integral symbols of dij(t) and Vij(t), respectively. Definition 2 (Isolation-State): In the distance and relative velocity plane Ωijshown in Fig.2, the plane constrained by(18), i.e., the blue area Ψij Ψij={(dij(t),Vij(t)):dij(t)≥daij(t)} (21) is defined as the isolation-area. xiand xjare in the isolationstate when the relative vector Dij(t) is in the isolation-area Ψi j. Definition 3 (Matching-State [2]): In the distance and relative velocity plane Ωijshown in Fig.2, after removing the collision-area and the isolation-area, the remaining plane, i.e.,the green area Πij 在开发及利用课程资源的过程中不能够任性妄为,而坚持原则能够对人们的行为进行一定的规范,指导人们正确的行为,在开发以及利用课程资源的过程中也需要一定的原则来进行规范。在收集到的资料中大多没有形成规矩没有顺序,不能够直接简单、盲目地投放到资源库中或直接使用。所以,为了能够充分地、合理地利用收集到的资料,应该进行筛选。在筛选的过程中应该遵循以下原则:个性化原则、发展性原则、生活性原则、适应性原则、科学性原则。 is defined as the matching-area. When the relative vector Dij(t) is in the matching-area, i.e., Dij(t)∈Πij, we say that xiand xjare in the matching-state, which means that xiand xjneed to communicate with each other and there will be no collision between them. Based on (6), (11), (17), and (22), we get the matching-state probability p(Πij) between xiand xjas follows: By combining Figs. 1 and 2, we can get the probability division of the three states as shown in Fig.3. Fig.3. Probability division of states between formation members. From Fig.3, we can observe that the probabilities of collision-state, matching-state, and isolation-state of flight members are the volumes formed by collision-area, matchingarea, and isolation-area on the probability density surface of Dij(t) in Fig.1, respectively. Definition 4 (Dynamic Adjacency Degree [2]): The dynamic adjacency degree naiof xiis the number of adjacent neighbors that are in the matching-state with xi. The dynamic proximity group of xiis where the group members satisfy Fig.10. MAF initial configurations and turning configurations of different dynamic adjacent degree. (a) line; (b) diamond; (c) two-line; (d) hexagon; (e) line turning; (f) diamond turning; (g) two-line turning; (h) hexagon turning. basic capability of MAF. Moreover, the quasi σ-adjacent is the most widely used one in practical application and is more suitable to describe the lattice-type of MAF. The system overview of one HIL flight member is shown in Fig.9(a), “NET” denotes network port communication,“COM” is serial communication, the green arrows denote the data link of formation flight control, and the red arrows denote the data link of member flight control. The HIL experiment system formed by seven aircraft is shown in Fig.9(b). It should be noted that each member of MAF consists of the formation control module, the flight control module, the flight simulation module, the virtual communication module, and the flight monitoring module, but not including the formation monitoring module. With the above HIL system, we design the line configuration (Fig.10(a)), the diamond configuration (Fig.10(b)), the two-line configuration (Fig.10(c)), and the hexagon configuration (Fig.10(d)), where the red dot and the white dot represent the central member and the adjacent members in the dynamic proximity group, respectively, and the numbers before and after the colon indicate the member number and flight altitude, respectively. In order to verify the influence of different dynamic adjacent degrees on the denseness and the basic capability of MAF configuration, we observe the collision probability and the configuration holding capability of the seven aircraft at it turns as shown in Figs. 10(e)–10(h). As shown in Fig.10(a), the dynamic adjacent degree of A4(A represents aircraft) is na4=2 and its adjacent members are A3 and A5; in Fig.10(b), the dynamic adjacent degree of A4 is na4=3 and its adjacent members are A0, A3, and A5; in Fig.10(c), the dynamic adjacent degree of A6 is na6=4 and its adjacent members are A1, A3, A4, and A5; in Fig.10(d),the dynamic adjacent degree of A6 is na6=6 and its adjacent members are A0, A1, A2, A3, A4, and A5. We can observe from Figs. 10(e)–10(h) that: i) when MAF is turning, the configuration on the inner side of the corner is squeezed, and the collision risks of the dynamic proximity group increase. The greater the dynamic adjacent degree, the smaller the safe space that can be used to avoid a collision, the greater the probability of dynamic proximity group collisionstate and the denser the MAF configuration. In other words,the hexagon configuration is the densest while having higher risks of being in the collision state, while the line configuration is the loosest and has more maneuver space to avoid collision; ii) when MAF is in turning, the smaller the dynamic adjacent degree of dynamic proximity group is, the better the configuration holds and the better the basic capability of MAF is. That is to say, the hexagon configuration owns the worse configuration holding capacity while the line configuration holds the best. The dynamic adjacent group’s collision probability and matching probability are calculated based on the results in Section III, the denseness and the basic capability classification are given based on the results in Tables I and III.Specific comparison data are shown in Table IV. Fig.11. MAF initial hexagon configurations and turning configurations of different expected distances. (a) µij=50.0 m ; (b) µij=60.0 m ; (c) µi j=74.0 m;(d) µ ij=90.0 m ; (e) turning of µ ij=50.0 m ; (f) turning of µ ij=60.0 m ; (g) turning of µ ij=74.0 m ; (h) turning of µ ij=90.0 m. TABLE IV COMPARISON DATA OF DIFFERENT DYNAMIC ADJACENT DEGREE In conclusion, if the task requires a relatively complex configuration with a higher adjacent degree like the hexagon configuration, the platform should be equipped with higher maneuverability to adjust the relative distance and velocity with higher frequency to avoid a collision. Due to the frequent adjustment in this case, the commander needs to be more tolerant with the bad MAF configuration holding ability. In order to verify the influence of different expected distances on the denseness and the basic capability of MAF configuration, we designed the hexagon configuration for MAF with different expected distances under the instruction of Result 1. In this paper, we chose to present four representative distances: µij=50.0 m (Fig.11(a), λdij0=0.0),µij=60.0 m (Fig.11(b), λdij0=2.0 ), µij=74.0 m (Fig.11(c),λdij0=4.8) , and µij=90.0 m (Fig.11(d), λdij0=8.0). We observe the collision probability and the configuration holding degree of the dynamic proximity group at the turn of MAF shown in Figs. 11(e)–(h). We can observe from Fig.11 that: i) when MAF is turning,the configuration on the inner side of the corner is squeezed,and the collision risk of the dynamic proximity group increases. The smaller the expected distance (or the static distance safe factor), the smaller the safe space that can be used to avoid collision, the greater the probability of dynamic proximity group collision-state and the denser the MAF configuration; ii) when MAF is turning, the closer to the expected distance, the better the configuration holds and the basic capability of MAF configuration improves. We got the expected distance 74 m after many tests which corresponding to a good basic capability of hexagon configuration, and the matching-state probability is relatively high compared with others. The collision probabilities and matching probabilities of the hexagon configuration with different expected distances are calculated based on the results in Section III, and their denseness and basic capability are graded based on the results in Tables I and III. Specific comparison data are shown in Table V. TABLE V COMPARISON DATA OF DIFFERENT EXPECTED DISTANCE The results reach a reasonable evaluation of MAF denseness and basic capability. It also arrives at the same conclusion as Result 4 that µijshould take the intermediate value of safety distance and adjacent distance. To be more specific, when µijis less than the safety distance, the collision probability between two formation members will increase; when µijis larger than adjacent distance, the isolation probability will increase. In order to guide the engineering applications better, we carried out MAF outfield flight tests after verifying the reasonability and safety of the designed configuration and expected relative distance in the HIL experiment. The denseness was evaluated quantitatively by the proposed method. Fig.12. Outfield flight test equipment. (a) Six UAVs; (b) The loads in the cabin of the UAV. Fig.13. MAF flight. (a) MAF flocking (before turning); (b) MAF flocking (turning). The experiment is composed of six unmanned aircraft as shown in Fig.12(a). One of them serves as the aerial photographic UAV to capture the configuration. The other five of them are equipped with the power module, the autopilot module, the formation cooperative guidance module,the formation communication module, the GPS, etc.(Fig.12(b)). The expected flight height is 200.0 m, the expected velocity is 25 m/s, the static safety distance is 50 m and the adjacent distance is 100 m. We set the height of the aerial photographic UAV to be 400 meters to capture the configuration. The specific comparison data of these MAF flight experiments are shown in Table VI. TABLE VI DATA FOR MAF FLIGHT EXPERIMENTS Note that we have applied collision avoidance algorithms to the formation control in outfield flight tests to keep the distance between two flight members always larger than the dynamic safe distance to ensure the safety of aircrafts. In summary, we verify the influences of the dynamic adjacent degree naiand the expected distance µij(or the static distance safe factor λdij0) on the denseness and the basic capability of MAF configuration respectively by the HIL simulation experiment and outfield flight test, and the experiment results are the same as the conclusions in Sections IV and V. Quantitative evaluation of formation collision-state and matching-state provides quantitative evaluation indicators for engineering practices. The feasibility of these two evaluation methods of MAF configuration is thus verified. In this paper, with the aim to evaluate high dynamic MAF configuration, the dynamic safety distance and dynamic adjacent distance which are related with relative velocity are introduced to divide the MAF states. Based on the division,the collision-state and matching-state probability models are built. Then the two evaluation methods of MAF configuration are studied: a) The denseness of MAF configuration,including the tightness (dense, tight, and loose configuration)and the scale (massive, large, medium, small, and adjacent configuration), are evaluated quantitatively by the probability of MAF collision-state. The influences of the static safety distance, the maximum relative acceleration, the distance standard deviation, the relative velocity standard deviation,the correlation coefficient of distance and relative velocity, the expected distance, and the expected relative velocity on the collision-state probability are analyzed. The methods to reduce the probability of MAF collision-state to strengthen the formation safety are given according to the evaluation. The MAF tightness and scale are graded based on the collisionstate probability; b) The basic capability of MAF configuration is evaluated quantitatively by the probability of MAF matching-state. In this process, the influences of the same factors in a) on the matching-state probability are analyzed, and the methods to increase the probability of MAF matching-state to strengthen the basic capability of MAF are given. In addition, based on the relative distance and the relative velocity, two lattice-type structures ( σ-adjacent configuration and the quasi σ-adjacent configuration) are compensated for the previous studies to grade the configuration basic capability, so that the lattice-type structure of configuration becomes more complete. Finally, hardwarein-the-loop simulation and outfield flight test results are presented to verify the rationality of these evaluation methods.
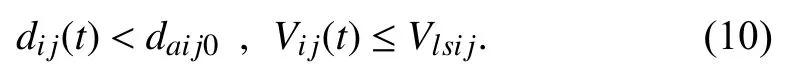



B. Dynamic Adjacent Distance


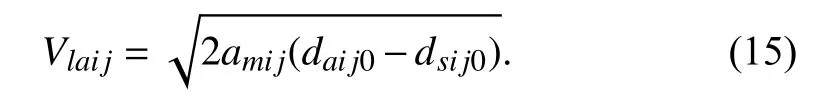

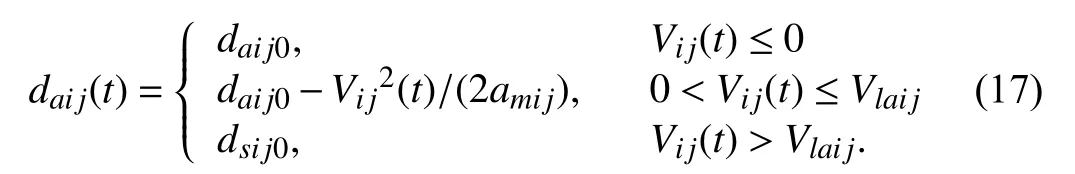

C. Two Formation Member’s States Division
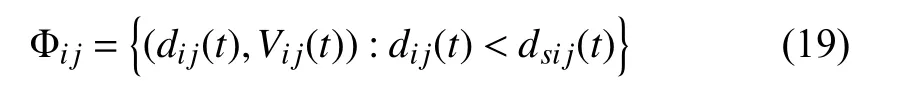




D. MAF States Division








VI. HIL EXPERIMENT AND OUTFIELD FLIGHT TESTS

A. System Composition
B. Comparative Experiment and Result Analysis of Different Dynamic Adjacent Degree


C. Comparative Experiment and Result Analysis of Different Expected Distances

D. Outfield Flight Test




E. Experiment Conclusion
VII. CONCLUSION
猜你喜欢
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Residual-driven Fuzzy C-Means Clustering for Image Segmentation
- Decoupling Adaptive Sliding Mode Observer Design for Wind Turbines Subject to Simultaneous Faults in Sensors and Actuators
- Task Scheduling for Multi-Cloud Computing Subject to Security and Reliability Constraints
- Vibration Control of a High-Rise Building Structure: Theory and Experiment
- Fixed-Time Output Consensus Tracking for High-Order Multi-Agent Systems With Directed Network Topology and Packet Dropout
- Property Preservation of Petri Synthesis Net Based Representation for Embedded Systems
