基于模糊故障树方法的脐带缆可靠性分析研究

2021-04-13刘洪磊

海洋工程 2021年2期

夏冉，刘洪磊，张洲，罗丹，张玉

(1. 中国石油大学(北京)，北京 102200； 2. 中海油信息科技有限公司天津分公司，天津 300450)

作为水下生产系统中部控制设备的重要装备之一，脐带缆是水上平台控制模块与水下生产系统以及水下生产系统各部分仪器设备之间相互连接的供能和通信管线，它主要承担着电力、液压动力等能源的供给，光纤通信和化学药剂等信号的传输(图1)，因此又被称为水下生产系统的“生命线”[1-2]。

自1961年荷兰壳牌在墨西哥湾使用第一条全液压软管脐带缆以来，随着技术的成熟和工作水深的增加，动力电缆单元和数据传输线路单元相继加入脐带缆构件的行列。直到1982年，瑞典公司Sandvik首次用钢管替代热塑性软管，并且高压输电方式开始应用，同时引入了铠装单元和光纤单元来完善脐带缆结构和功能[2]。文中所研究的脐带缆为双层钢丝铠装脐带缆，其典型结构如图2所示[3]。

图1 水下生产系统中的脐带缆Fig. 1 Umbilical in subsea production system

图2 脐带缆典型结构Fig. 2 Typical structure of umbilical

随着应用水深的增加，造成脐带缆失效的因素也更多，脐带缆的失效会引起整个水下生产系统的失效，导致严重的生产事故。脐带缆的失效模式为脐带缆在储存、安装及在位等工况下受到海洋环境荷载作用时可能发生的破坏形式[4]，主要包括以下几种形式：

1) 拉伸失效。脐带缆在位运行过程中，随着水深的增加，脐带缆顶部拉伸荷载增加。当拉伸荷载超过一定范围后，会导致钢材料等承载构件失效或电缆、光缆等构件变形过大无法正常工作从而导致拉伸失效。

2) 疲劳失效。由于海洋环境复杂多变，脐带缆运行期间承受波浪、海流及浮体运动产生的交变拉弯荷载，铠装层和钢管受到交变应力产生损伤累积达到疲劳破坏。

3) 腐蚀失效。脐带缆在位运行过程中，脐带缆外部暴露在海水中，外部海水环境会对其产生腐蚀作用导致腐蚀失效。此外，钢管内部输送的介质也会对钢管有腐蚀作用。

4) 屈曲失效。在脐带缆安装及在位运行时，脐带缆触地点由于海床反作用力会导致脐带缆铠装层受到压缩荷载，产生“鸟笼现象”及整体屈曲或过度弯曲。

5)压溃失效。随着水深的增加，海水对脐带缆的静水压力不断增加，会导致管单元压溃失效而导致压溃失效。

6) 扭转失效。脐带缆安装过程中，脐带缆端部承受扭矩载荷作用时，由于触地点的张力非常低，极易形成扭转回路，当脐带缆弯曲半径小于临界值将会发生扭转失效。

由于脐带缆结构复杂多样，缺少基础可靠性数据，同时其不同于陆地上的工程结构，脐带缆应用环境位于深海海域，外界载荷的随机性更是不可忽略的重要影响因素，因此对其进行可靠性分析仍是一个难题，目前对海洋工程结构的可靠性研究主要集中在海洋平台结构以及其他海洋管线。王茜和赵建平[5]采用故障树法对引起海底管道第三方破坏失效的各个因素进行了分析，建立了第三方破坏故障树。董玉华等[6]分析了长输管线的失效状况，根据管线失效的两种主要模式建立了管线失效的故障树。Hu等[7]基于模糊故障树完成海底采油系统的油气泄漏风险分析。张磊等[8]通过引入“安全—中介—失效”工作模式，从安全、中介、失效3个方面反映长输管线系统的可靠性，建立了具有中介状态长输管线系统失效故障树模型。许文虎等[9]基于故障树分析方法对脐带缆进行了可靠性定性、定量分析，建立了目标脐带缆的故障树模型，但此模型仅考虑了脐带缆内部构件的故障，并未考虑引起构件失效的随机性因素。

因此，基于模糊故障树分析方法，综合考虑脐带缆工作环境的随机性因素，建立了脐带缆失效故障树模型，并通过定性分析及定量分析获得底事件失效概率和顶事件失效概率。

1 脐带缆失效故障树的建立

故障树分析(FTA)是一种由上往下的演绎式失效分析法[10]，它可以利用布林逻辑组合低阶事件并分析系统中不希望出现的状态。以顶事件作为分析的目标，通过逐层向下推溯所有可能造成顶事件发生的原因，找出各种底事件与顶事件之间的逻辑关系[11-12]。

对于“双层钢丝铠装脐带缆”的失效，根据故障树建立时顶事件的确定原则，选择“脐带缆失效”作为顶事件。引起脐带缆失效的最直接原因是“钢管”、“护套/铠装”和“电缆”等构件的失效破坏。这3种原因中的任意一个均会导致脐带缆失效，因此以这3个原因作为次顶事件，各部件的主要失效模式便是脐带缆失效故障树的中间级事件，而引起这些失效模式发生的随机因素则是故障树的底事件。使用FreeFta软件绘制的深水脐带缆故障树模型如图3、4所示，故障树中的事件描述如表1所示。

图3 脐带缆失效故障树Fig. 3 Fault tree of umbilical failure

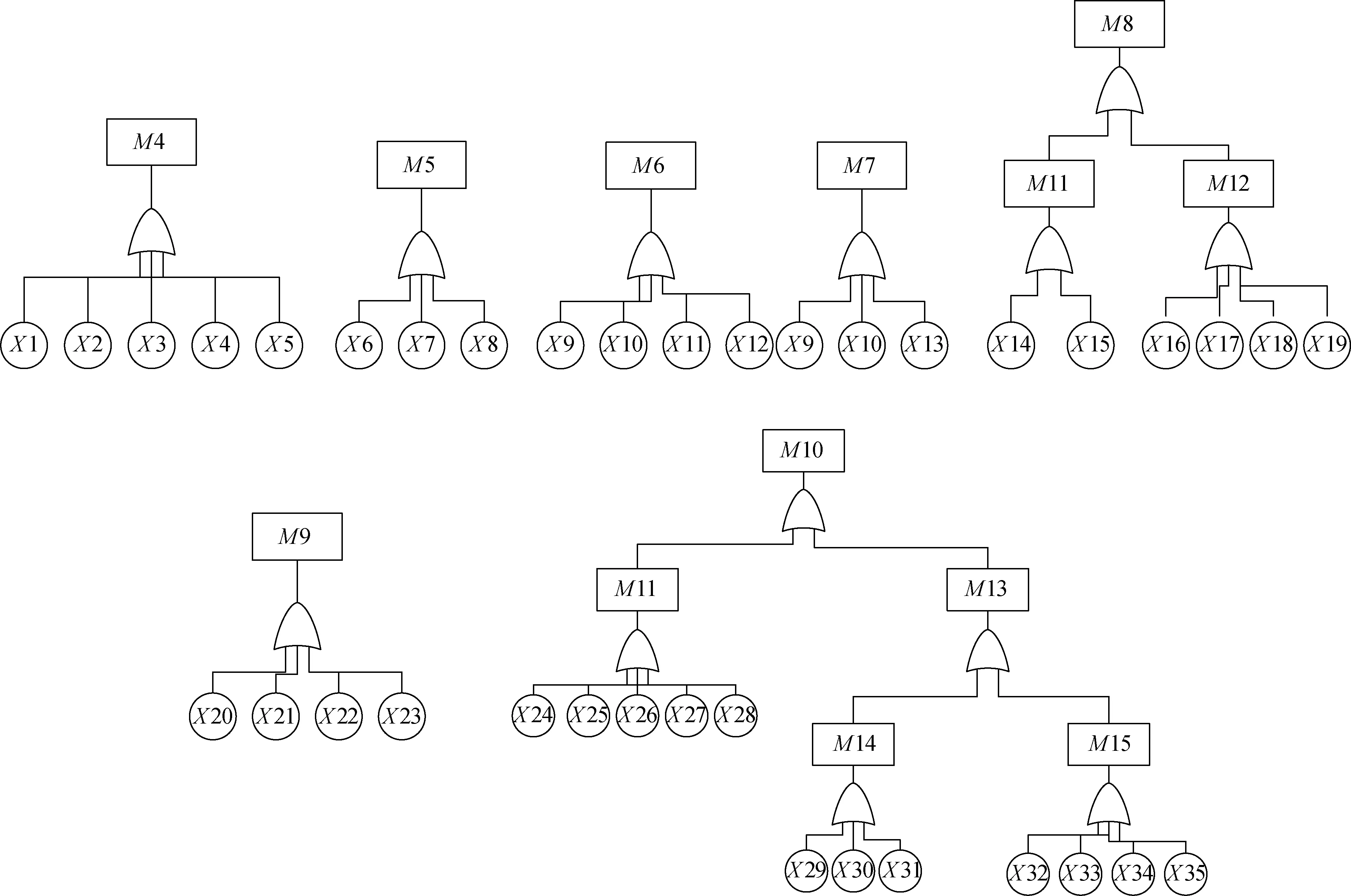
图4 脐带缆失效故障树各失效子树Fig. 4 Sub-failure trees of umbilical failure

表1 脐带缆失效故障树各符号意义Tab.1 The meaning of symbols in failure tree of umbilical

2 脐带缆失效故障树的定性分析

为了能够更为准确的找出脐带缆运行中的薄弱环节，使脐带缆的维护能够做到有的放矢，使用下行算法求解最小割集, 其基本原理是故障树中的或门增加割集数目, 与门增大割集容量 (割集中包含底事件数目), 从而将故障树转化为等效的布尔代数方程所示的标准表达式(1)[13]。

T=X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11+X12+X13+X14+X15+

X16+X17++X18+X19+X20+X21+X22+X23+X24+X25+X26+X27+X28+

X29×X32+X29×X33+X29×X34+X29×X35+X30×X32+X30×X33+X30×

X34+X30×X35+X31×X32+X31×X33+X31×X34+X31×X35

(1)

由式(1) 可见，脐带缆失效故障树一共包含40个最小割集，其中28个1阶最小割集，12个2阶最小割集。

1阶最小割集包含的底事件为X1～X28，故这28个底事件引起系统失效的概率最高，重要性记为1。2阶最小割集包含的底事件为X29～X35，其中底事件X29～X31在最小割集中出现的次数为4，故其引起系统失效的概率较高，重要性记为2;而底事件X32～X35在最小割集中出现的次数为3，故其引起系统失效的概率比底事件X29～X31更低，重要性记为3。脐带缆故障树模型中各底事件的重要性排序见表2。

为了保障脐带缆的运行安全、提高脐带缆的可靠性，在脐带缆设计、施工和运行过程中应当对引起脐带缆失效的概率最高一阶最小割集的28个底事件加以重点监控，同时提高其防护措施。

3 基于模糊理论的故障树定量分析

脐带缆失效故障树的定性分析无法计算出顶事件概率，故为了确定脐带缆的失效概率以及各构件对脐带缆失效的影响程度等还需要对其进行定量分析。由于目前缺少这些事件的概率统计，因此采用专家判断与模糊集数结合的方法计算底事件发生的概率，最终得到顶事件的可靠性[14-15]。

3.1 选取专家

首先对专家进行选取，选取的专家至少有5 a的相关工作经验，并且这些专家的工作领域要有所区别，如设计、安装、维护。每位专家根据其职称、学历、经验分别赋予分数，三者和为这位专家的总加权分数，每位专家的加权分数与所有专家的总分数的比值为每位专家的权重因子，表3列出了20位专家的权重因子。

3.2 将语言文字转化为模糊数

将专家判断过程中的“很小”、“小”、“较小”等自然语言转化为模糊数[16-17]，转化比例如图5所示。

依照图5所示，由自然语言的模糊数表现形式得出的隶属度函数表达式如下：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

式(2)～(8)分别是专家判断的自然语言所对应的隶属度函数。对某一基本事件Xi来说，其20位专家的语言评论可以通过方程(9)转换为模糊数[18]。

(9)

其中，wj是专家j的权重因子(表3)，Ai j是由专家j给出的自然语言表达式转换的模糊数，Mi是基本事件Xi的失效概率。因此，每个基本事件的失效概率都可以通过这种方法评估计算出来。

使用模糊集的截集和平均算法对20位专家的评估意见进行综合处理，设式(2)～(8)的α截集分别为：VLα=[g1,g2],Lα=[l1,l2],FLα=[f1,f2],Mα=[m1,m2],FHα=[k1,k2],Hα=[h1,h2],VHα=[s1,s2]。以fFL(x)为例，令α=(x-0.2)/0.1，则f1=0.1α+0.2,f2=0.5-0.1α；同理可得，g1=0，g2=0.2-0.1α，l1=0.1α+0.1，l2=0.3-0.1α，m1=0.1α+0.4，m2=0.6-0.1α，k1=0.1α+0.5，k2=0.8-0.1α,h1=0.1α+0.7,h2=0.9-0.1α,s1=0.1α+0.8,s2=1。

以底事件X5“工作平台移位或倾斜”为例进行计算，在α截集下20位专家评价的模糊数为:

W=max|fVL(x)∧fL(x)∧fFL(x)∧fM(x)∧fFH(x)∧fFL(x)∧fH(x)∧fM(x)∧

fM(x)∧fFH(x)∧fH(x)∧fVH(x)|=|(0.1α+0.248 4),(0.469 4-0.1α)|

(10)

令Wα=|(z1,z2)|=|(0.1α+0.248 4),(0.469 4-0.1α)|，则有:

(11)

所以，可得模糊数W的关系函数为：

(12)

3.3 将模糊数转化为失效概率

专家判断的自然语言转换的模糊数是个模糊集合，在故障树分析中很难直接带入计算。因此，需要把模糊数转化为一个清晰值，即模糊可能性值FPS[19]。依据Chen和Hwang[14]提出的左右模糊排序法可把模糊数转化为FPS，该方法定义的最大模糊集fmax(x)和最小模糊集fmin(x)分别为：

(13)

(14)

则平均模糊数的左模糊数可能性值FPSL和右模糊可能性值FPSR分别为：

FPSL(W)=supx[fW(x)∧fmin(x)]=0.426 7
FPSR(W)=supx[fW(x)∧fmax(x)]=0.683 3

(15)

则平均模糊数W的模糊可能性值FPST(W)为：

(16)

为了保证失效率和模糊失效率之间的一致性，需要通过式(17)～(18)把模糊可能性值FPS转化为模糊失效率FFR，如下：

(17)

(18)

将式(16)计算得到的FPST=0.440 2代入式(17)，可得FFR=3.214×10-3，这就是基于专家判断和模糊数方法计算的底事件X5“工作平台移位或倾斜”发生的概率。采用同样的方法可求得脐带缆失效故障树其它基本事件发生的概率。

用E1，E2，……，E40来表示目标脐带缆的最小割集，则目标脐带缆顶事件T的失效概率Q为:

Q=P(T)=P(E1∪E2∪……∪E40)=P(E1+E′1E2+E′1E′2E3+……+E′1E′2……E′39E40)

(19)

根据公式(19)计算得出脐带缆的失效概率为0.019 12，可靠度为0.980 88，即可靠度指标为2.39，符合水下生产系统深水项目的一般要求[20]。

其中护套/铠装失效(M2)的概率为0.007 45，钢管失效(M1)的概率为0.007 21，电缆失效(M3)的概率为0.005 14，则可以得出护套/铠装比其他单元失效概率大的结论，说明护套/铠装对脐带缆系统的可靠性影响最大，钢管的失效概率次之。

护套/铠装的主要失效模式是拉伸断裂失效、径向失效及侧向失效，而钢管的主要失效模式为拉断失效。对脐带缆截面以及护套/铠装和钢管的几何尺寸进行合理的设计，能有效的降低护套/铠装和钢管的拉伸断裂失效概率；对脐带缆铠装钢丝的螺旋角进行合理的设计，使其有更小的曲率半径，降低其发生侧向(弯曲)失效的概率；此外，在铠装层外布置防鸟笼失效层也能有效的预防护套/铠装的径向失效。