一种基于状态空间模型的浮式海上升压站平台动力响应计算方法研究

汤群益，孙震洲，陈杰峰，金 磊

(1. 浙江省深远海风电技术研究重点实验室，浙江 杭州 311122； 2. 中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122； 3. 三峡新能源山东昌邑发电有限公司，山东 潍坊 261300)

随着海上风电建设的推进，海上风电逐渐由近海走向深海，为了适应海上风电的发展趋势，海上风电场中的海工结构物结构型式也由固定式转变为浮式。作为电力输送、汇集的枢纽，浮式海上升压站的安全性对海上风电场的健康运营至关重要。相比于固定式升压站，浮式海上升压站在6自由度上的响应更为明显，这也给升压站中的电气设备带来较大的安全隐患[1]。因此，需要在设计阶段对浮式海上升压站结构进行动力响应分析，进而优化其水动力性能，保障浮式海上升压站的平稳运行。

基于势流理论，同船体等浮式结构相同，浮式海上升压站的运动常采用Cummins方程进行描述[2]。为了求解Cummins方程得到浮式结构的动力响应，常用的方法包括时域法和频域法。频域法通过傅里叶变换，在频域内求解Cummins方程，避免卷积项积分。但在运算时应用傅里叶变换，会导致傅里叶变换漏频、能量泄露等局限性突显[3]，并且无法计算浮式结构瞬态响应。时域法又可分为直接时域法和间接时域法。直接时域法直接在时域内构建求解速度势的初边值偏微分方程，通过求解时域格林函数来分析浮式结构物的动力响应。直接时域提出时间较早，但在求解浮式结构的水动力过程中，面临计算量大、分析效率低等问题。相比直接时域法，间接时域法采用频域势流理论计算浮式平台的水动力参数及波浪力，通过傅里叶变换将上述频域水动力参数和波浪力转化到时域，从而在时域内求解浮式结构的动力响应。间接时域法能够分析浮式结构的瞬时动力响应，并且比直接时域法的计算效率高。然而，间接时域法求解浮式结构的动力响应时，依赖于卷积运算，从而消耗大量计算资源[4]。同时，间接时域法由于高频位置的水动力系数难以精确求得，对最终的动力响应求解造成难以控制的误差[5]。针对这些问题，一种思路是通过状态空间模型来代替线性卷积项，从而提高浮式结构动力响应分析的计算速度和精度。对于此，学者们展开了大量研究。Schmiechen[6]将状态空间模型和船体的瞬态响应建立起联系。Xia等[7]也在相关海洋结构物的水动力分析中使用了状态空间模型并进行了深入研究。Sutulo和Guedes[8]进一步提出可以用状态空间形式来表达辐射力，进而代替传统时域方程中的卷积项。Taghipour等[9]应用时域方程直接计算卷积方法和状态空间方法做了相应的算例分析，并给出了方法的详细介绍。然而，这些方法大多通过对兴波阻尼进行余弦变换得到延迟函数，进而求解对应的状态空间模型。此过程采用梯形积分法计算延迟函数，额外引入计算误差。

为了解决卷积项导致浮式海上升压站动力响应分析效率低及采用梯形积分法引起计算误差的问题，提出了一种基于状态空间模型的浮式海上升压站动力响应分析方法，同时运用附加质量和兴波阻尼在频域内计算延迟函数对应的状态空间，从而提高浮式海上升压站动力响应的分析效率和精度。通过将文中方法应用于日本福岛浮式海上风电示范项目中的浮式升压站模型[10]，并与商业软件SESAM[11]计算结果进行对比，检验文中方法的正确性和有效性。

1 基础理论

1.1 浮式平台运动方程

在势流理论的假设条件下，只考虑一阶水动力作用，无航速海上浮式结构的运动方程可以用Cummins方程表示：

(1)

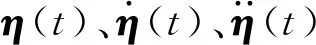
1.2 Oglivie关系式

Cuminns方程中附加质量A和延迟函数K(t)是与海上浮式结构水动力参数相关的量，为探讨它们之间的数学关系，对式(1)进行傅里叶变换[12]：

(2)

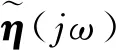
Ogilvie通过对船体运动预测的研究，建立了随频率变化的附加质量A(ω)及兴波阻尼B(ω)与延迟函数K(t)的关系式，即[10]：

(3)

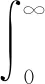
(4)

延迟函数K(t)的傅里叶变换通过A(ω)和B(ω)可表示为：

(5)

由式(3)可知，式(1)中附加质量为：

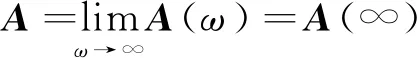
(6)

从而，式(1)可表示为：

(7)

2 状态空间模型频域算法

2.1 频域线性回归拟合

(8)

对式(8)进行Laplace变换，即可得到该系统的传递函数。传递函数与脉冲响应函数为一对Laplace变换对，从而得到：

(9)

式(5)中的水动力参数A(ω)和B(ω)能够通过SESAM软件提取，由于海上浮式结构的水动力参数无法通过解析的方式得到解析解，只能通过数值方法计算其离散值。式(5)和式(9)可以通过关系式s=jω建立联系，根据离散值在频域内估算浮式结构的传递函数表达式，即：

(10)

式中：

(11)

由式(10)可知传递函数的有理分式形式是关于θ的函数，求解式(10)中θ的常用方法包括非线性最小二乘拟合法[14]、拟线性频域回归法[15]及权重迭代频域拟合法[16]。这几种方法在实际应用中有各自的优缺点，文中采用权重迭代法对延迟函数的Laplace变换进行频域线性回归拟合，其计算公式为：

(12)

其中，

(13)

通过几次迭代后，式(12)会很快收敛，即θk≈θk-1，从而估算出式(10)中有理分式的分子和分母系数，即得到系统传递函数表达式。

2.2 状态空间模型构建

传递函数的有理分式可以等价地转化为极值—留数的和式形式，即：

(14)

式中：λik,l为该输入输出系统的极值，γik,l为对应的留数。

式(14)中的极值为分母Q(s)=0的根，可以通过求解下式获得。

sn+qn-1sn-1+……+q1s+q0=0

(15)

将式(15)的根s=λik,l代入下列极限公式中，对应的留数为：

(16)

由式(15)～(16)得到的卷积项对应系统的极值和留数，从而可以构建该系统的状态空间模型，即:

(17)

其中，

(18)

2.3 动力响应计算

通过上述方法得到各延迟函数对应的状态空间模型，将各自由度的状态空间模型进行组装，得到浮式结构的运动方程卷积项整体状态空间模型，并代入式(7)中，得到：

(19)

其中，Z(t)为组装后的状态向量，并且有：

(20)

其中，A′、B′、C′为Aik、Bik、Cik组装后的状态空间矩阵。

为求解式(19)和(20)，计算浮式结构的动力响应，对式(19)和(20)进行变形，并联立得到新的状态空间方程，即：

(21)

式中：v(t)为浮式结构的速度向量。

采用四阶龙格—库塔法对式(21)进行积分，进而得到浮式结构在外荷载作用的动力响应。

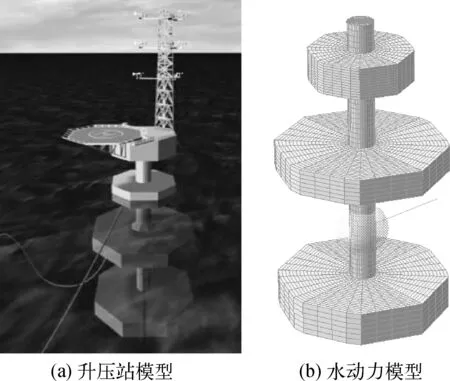
图1 浮式海上升压站Fig. 1 Floating offshore substation

3 数值算例

采用的数值模型为日本福岛浮式风电示范项目的改进Spar浮式海上升压站模型，如图1所示。该浮式升压站总高110 m，上部为甲板和塔台结构，下部浮式基础为立柱式平台，由中央立柱和三层舱体组成。三层舱体为八边形柱体，由中部和上部舱体提供浮力，下部舱体压载。浮式海上升压站工作水域水深120 m，吃水为50 m。根据浮式海上升压站的物理尺寸，采用SESAM软件建立水动力模型，计算结构的水动力参数，进而通过提出的基于状态空间模型动力响应分析方法计算浮式结构的动力响应。

3.1 水动力参数

浮式海上升压站的附加质量A(ω)和兴波阻尼B(ω)由SESAM软件提取。根据浮式海上升压站的尺寸可知，该浮式结构的几何模型同时关于xoz平面和yoz平面对称，从而使其水动力参数具有特殊的对称性质。根据势流理论，A(ω)和B(ω)分别对应辐射力的实部和虚部，从而具有相同的对称性质，以A(ω)为例，有如下关系式：

A11(ω)=A22(ω)，A15(ω)=A51(ω)，A24(ω)=A42(ω)，A44(ω)=A55(ω)

(22)

因此，在计算浮式升压站的动力响应时，只有A11(ω)、A15(ω)、A24(ω)、A33(ω)、A44(ω)和A66(ω)等6个位置的水动力参数参与计算。这6个位置的水动力参数随入射波频率变化如图2所示。

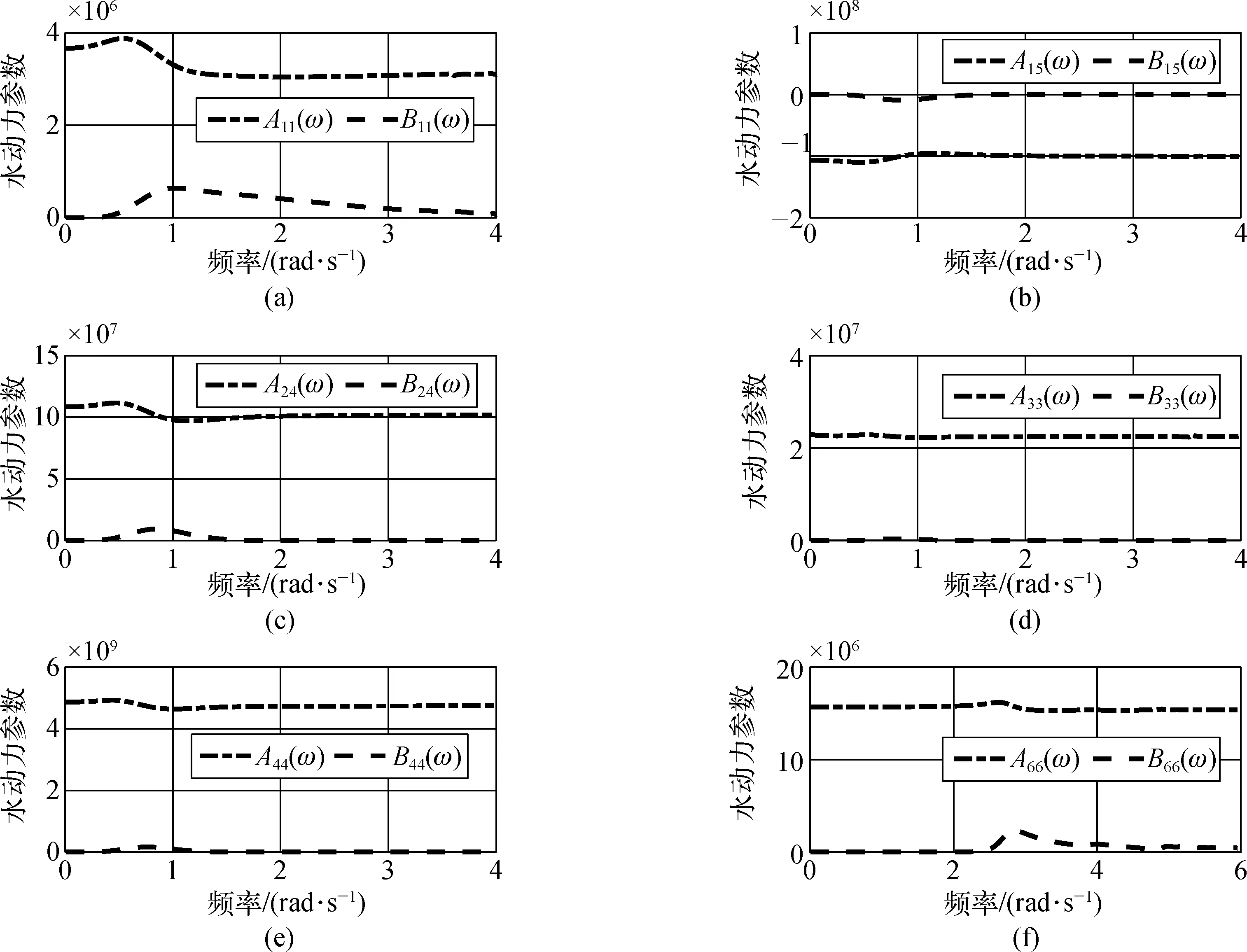
图2 附加质量A(ω)和B(ω)随频率变化Fig. 2 Curve of added mass A(ω) and B(ω) with frequency

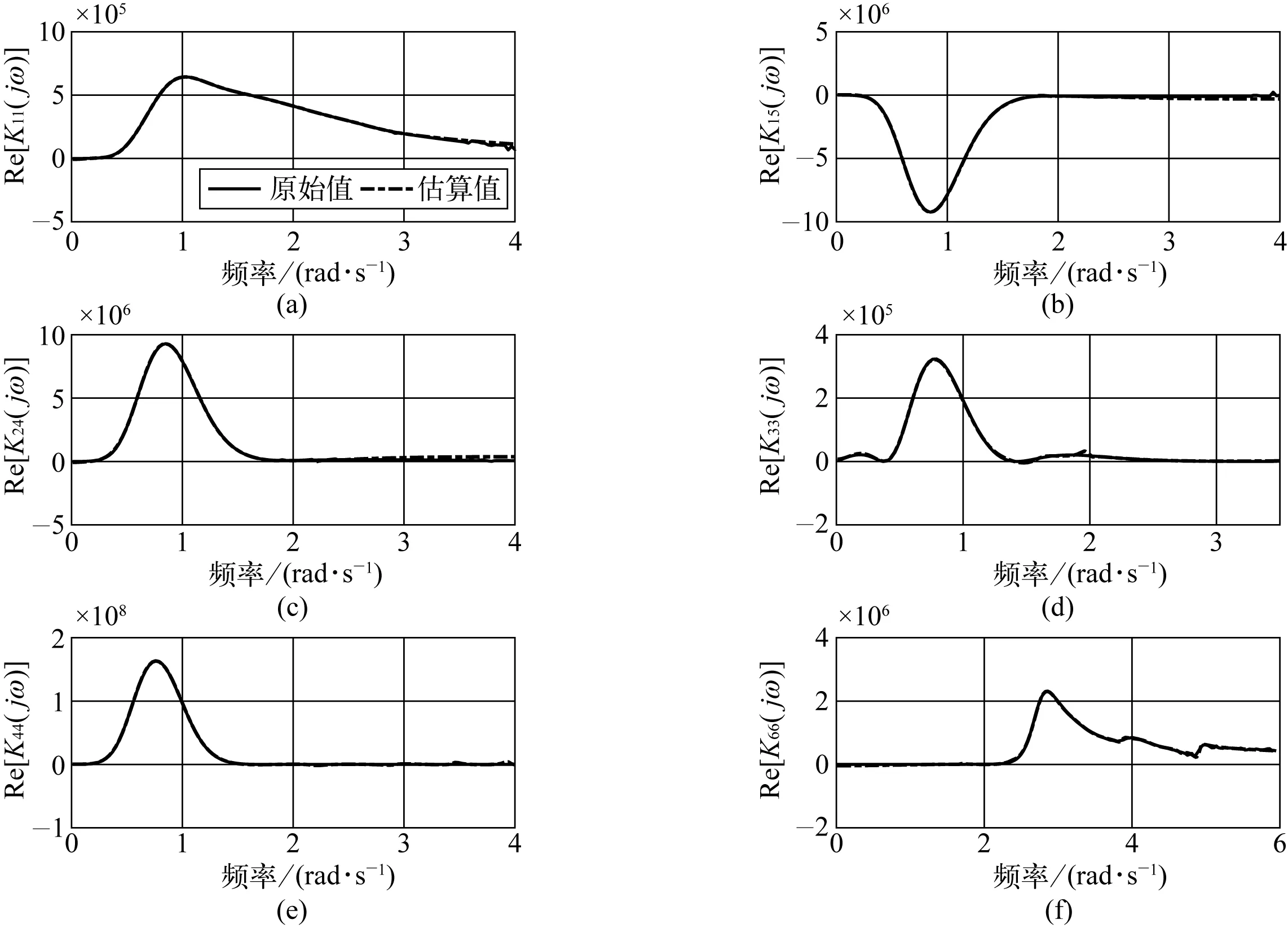
图3 估算延迟函数傅里叶变换与原始值的实部对比Fig. 3 Real part comparison between estimated delay function Fourier transform and original value

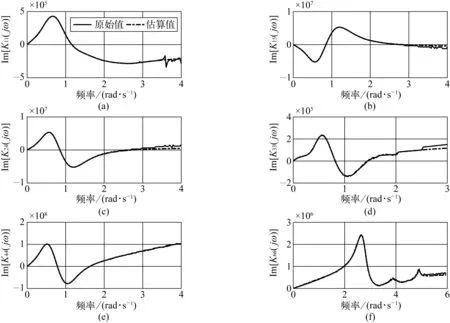
图4 估算延迟函数傅里叶变换与原始值的虚部对比Fig. 4 Imaginary part comparison between estimated delay function Fourier transform and original value

3.2 浮式升压站动力响应分析

图5 浮式海上升压站RAOFig. 5 RAO of the floating offshore substation

为了验证方法的正确性，通过商业软件SESAM的Wasim模块计算浮式海上升压站在波浪荷载作用下的动力响应，将其作为参考值评估文中方法计算结果的正确性与有效性。分析浮式海上升压站的动力响应之前，先通过SESAM计算浮式结构的RAO。当入射波的方向为0°时，浮式海上升压站平台的RAO如图5所示，即纵荡、垂荡和横摇自由度上有响应，横荡、纵摇和艏摇自由度上的响应为零。因此，只对比浮式海上升压站的纵荡、垂荡和横摇3个自由度的动力响应。

实际海域中的波浪多为不规则波，采用Jonswap谱模拟浮式海上升压站所在海域的不规则波，其参数如表1所示。入射波的方向为0°，从工况1到工况2，海况条件由温和变恶劣，两种工况下作用于浮式海上升压站的波浪力如图6和7所示，波浪力在横荡、纵摇和艏摇自由度上为零。

表1 各工况入射波浪参数Tab. 1 Incident wave parameters under various working conditions

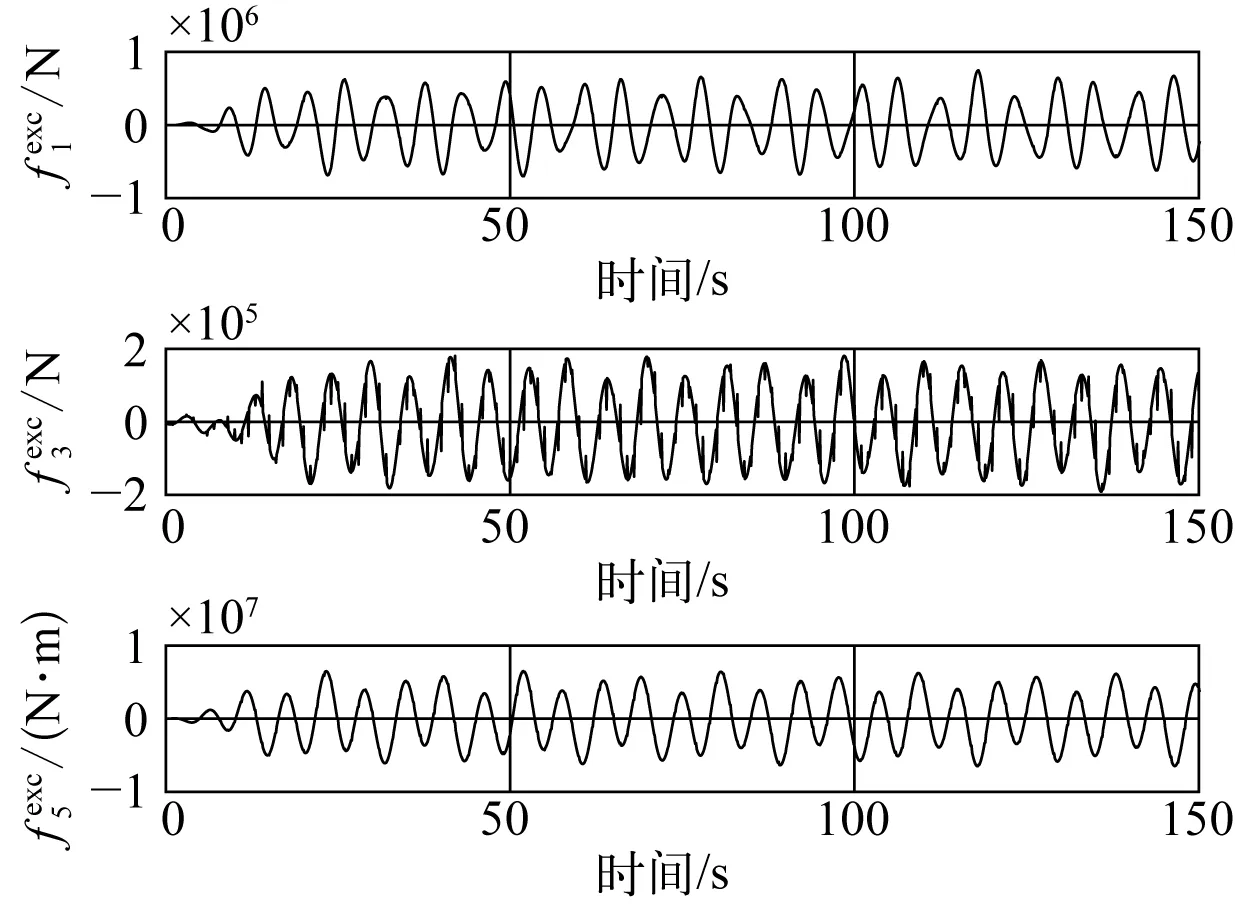
图6 工况1波浪力Fig. 6 Wave force of working condition 1

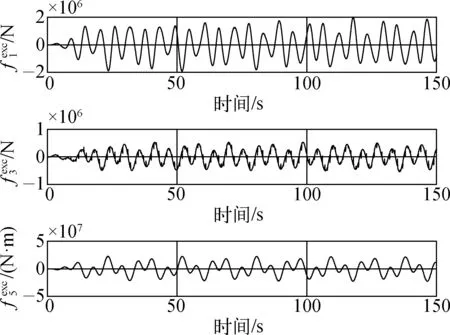
图7 工况2波浪力Fig. 7 Wave force of working condition 2

通过SESAM中的Wasim模块提取浮式海上升压站的质量矩阵M、附加质量矩阵A(∞)和静水恢复力系数矩阵C，其结果如下：

(23)

(24)

(25)

将上式及上节估算的状态空间模型代入式(21)中，并运用四阶龙格—库塔法求解该状态空间方程，从而得到浮式海上升压站在波浪荷载作用下的动力响应。在工况1和工况2条件下，采用文中方法计算得到浮式海上升压站纵荡、垂荡和横摇自由度的响应与Wasim计算结果对比如图8和10所示。从对比结果可知，在上述两种工况下，文中基于状态空间模型的浮式海上升压站动力响应计算方法得到的结果与商业软件SESAM计算结果吻合较好，二者计算结果的差异如图9和11所示，证明文中方法的正确性。

图8 工况1动力响应对比Fig. 8 Dynamic response comparison of working condition 1

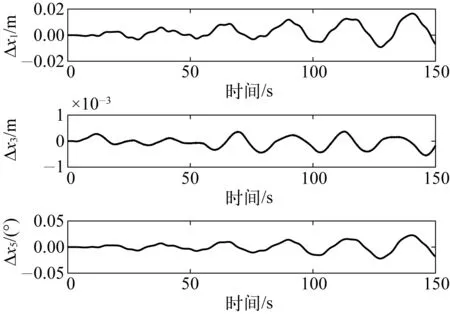
图9 工况1文中方法与WASIM计算结果差异Fig. 9 Difference between the method in this paper and Wasim calculation results of working condition 1

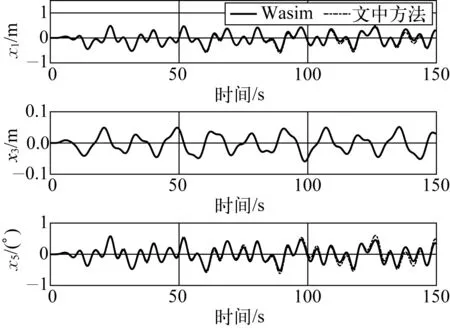
图10 工况2动力响应对比Fig. 10 Dynamic response comparison of working condition 2

图11 工况2文中方法与WASIM计算结果差异Fig. 11 Difference between the method in this paper and Wasim calculation results of working condition 2

同时，采用状态空间模型代替Cummins方程中的卷积项，避免时域积分时卷积项运算消耗大量计算资源的情况，从而提高了浮式海上升压站动力响应分析的效率。

4 结 语

提出了一种新的浮式海上升压站动力响应分析方法，该方法根据频域内线性回归拟合，通过附加质量和兴波阻尼，估算延迟函数对应传递函数的有理分式形式，进而计算延迟函数的极值和留数，再由极值和留数构建延迟函数对应的状态空间模型，从而使用状态空间模型代替Cummins方程中的卷积项，最后通过四阶龙格—库塔法计算浮式海上升压站的动力响应。与传统的时域积分方法相比，文中方法通过状态空间模型代替Cummins方程卷积项，不同于SESAM中的频域方程和直接时域方法，为间接时域方法的延伸，避免了卷积项计算导致的误差积累，同时提高了动力响应分析效率。

文中以日本福岛浮式海上风电示范项目的浮式升压站为研究对象，提取其附加质量和兴波阻尼，估算延迟函数的状态空间模型，从而计算浮式升压站在两种不规则波作用下的动力响应，并与SESAM软件计算结果对比，二者结果吻合较好，说明文中方法的正确性。