基于EGARCH和Cornish-Fisher展开的VaR度量方法*

魏正元，王 雪，杨 丹，杨书悦

(重庆理工大学 理学院，重庆 400054)

0 引 言

VaR(Value at Risk，风险价值)方法已成为目前金融界测量市场风险的主流方法，它衡量了一个金融头寸在给定的持有期l和置信水平α(0<α<1)下由于市场变动可能发生的最大损失量。令X表示在持有期l内金融头寸价值的改变，一个多头头寸在持有期的VaR定义为X的α分位数[1]：VaRα=inf{x:P(X≤x)≥α}。GARCH类模型能较好地描述收益波动率的演变，曹志鹏等[2]在对比经典套期保值比率优劣的基础上,构建了以GARCH(1,1)为基础的VaR最优动态套期保值模型；于孝建等[3]提出了对股票收益VaR值进行度量的M-Realized GARCH模型；黄崇珍等[4]基于GARCH模型计算了华夏沪深300ETF联接在厚尾性的t分布和GED分布下的风险值；Lu等[5]将Copula函数与GARCH模型相结合，构造了条件联合分布，用于估计能源市场中原油期货和天然气期货等权重投资组合的风险价值VaR。

Cornish-Fisher展开方法能对收益率分位数进行有效展开。魏正元等[6]针对小样本情形下的收益率序列，运用Cornish-Fisher展开方法计算VaR值;极值理论(EVT)在风险度量中的应用越来越广泛，梁媛等[7]借用EVT能够刻画极端损失的优势建立了EVT-ARMA-EGARCH-M和EVT-ARMATGARCH-M两种模型捕捉收益分布的粗尾评估金融市场的极端风险；基于Bootstrap的VaR度量方法备受关注，Swensen等[8]研究了包含平稳回归的降秩向量自回归VaR模型的Bootstrap算法。

EVT能够较好地捕捉收益率出现极值的情况，Bootstrap方法度量VaR时不需要对收益率的分布做任何假设，但EVT和Bootstrap不能刻画收益率的波动聚集性，GARCH族模型克服了这一弱点。以往的研究中选用的GARCH模型不能体现资产收益率序列的非对称效应，本文将EGARCH模型与Cornish-Fisher展开相结合，通过迭代EGARCH模型的波动率方程计算出收益率序列的偏度和峰度，把计算所得的偏度和峰度代入Cornish-Fisher展开式，再用Cornish-Fisher展开对收益率VaR进行度量，称这种VaR度量方法为VaRGARCH-CF方法。为了方便比较，将经典的基于极值理论的VaR方法称为VaREVT方法，基于Bootstrap度量VaR的方法称为VaRBS方法。最后, 取样标普500指数1990-01-01—2020-03-31收益率数据，将研究的方法与其他两种方法进行了对比测试, 评述了3种方法的优劣。

1 模型与预备知识

1.1 EGARCH模型

Nelson(1991)提出了EGARCH模型:

1.2 Cornish-Fisher展开

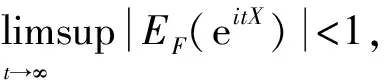
(1)

其中：zα为标准正态分布的α分位数，κ3和κ4分别表示总体分布X的偏度和峰度。

1.3 Bootstrap 方法

当X1,X2,…,Xn是来自总体X～F(x)的iid样本,样本次序统计量为X(1),X(2),…,X(n)，可用Bootstrap方法估计其样本p分位数：

其中：l=np，l1和l2表示与l相邻的两个数，li=pin。

从样本X1,X2,…,Xn中随机抽取B个Bootstrap子样本；计算每个Bootstrap 子样本的样本p分位ξp,i(i=1,…,n)，VaRBS为B个Bootstrap 子样本分位数的均值：

1.4 EVT方法

设X1,X2,…,Xn是来自总体分布X～F(x)的iid样本，给定一个阈值u，当X>u时，X为极值，Y=X-u为超额。超额分布函数为

Fu(y)=P{X-u≤y|X>u}=

F(x)=(1-F(u))Gξ,β(x-u)+F(u)

其中：Gξ,β(·)为GPD值，ξ为GPD的形状参数，β为GPD的尺度参数。

给定概率p>F(u)，得到

2 VaREGARCH-CF方法

定理1 若收益率Xt的扰动at满足EGARCH(1,1)模型，Xt的分布函数为F，则分位数的Cornish-Fisher展开为

证明EGARCH(1,1)表示为

Xt=ut+at,at=htεt,εt～N(0,1)

迭代运算得到：

α0+α1(|εt-1|-rεt-1)+

β1[α0+α1(|εt-2|-rεt-2)+β1ln(ht-22)]

…=

E[αt]=E[htεt]=E[ht]E[εt]=0

由中心化不改变偏度和峰度，Xt的偏度和峰度为

将偏度S和峰度K代入式(1)得到：

ut和σt分别为基于EGARCH(1,1)的条件均值和条件标准差，基于定理1得到VaREGARCH-CF对VaR的度量为

3 实证分析

选取标普500指数1990-01-01—2020-03-31共7 620个收盘价Pt进行实证分析。从多头的角度考虑t时刻的收益率rt=-(log(Pt)-log(Pt-1))。

图1是标普500收益率时序图，该图显示收益率异常值出现的频率比较高并显示出波动聚类的现象。表1是标普500指数的描述性统计表，其中收益率的峰度大于3，表明收益率序列存在明显的尖峰特征，收益率的偏度为正，说明收益率序列是非对称的，这和金融序列大多存在偏态是相符合的[12]。收益率JB统计量显示出收益率具有非正态性，ADF检验统计量和LM检验统计量表明收益率平稳且具有ARCH效应，将选用EGARCH模来对标普500收益率序列进行建模。

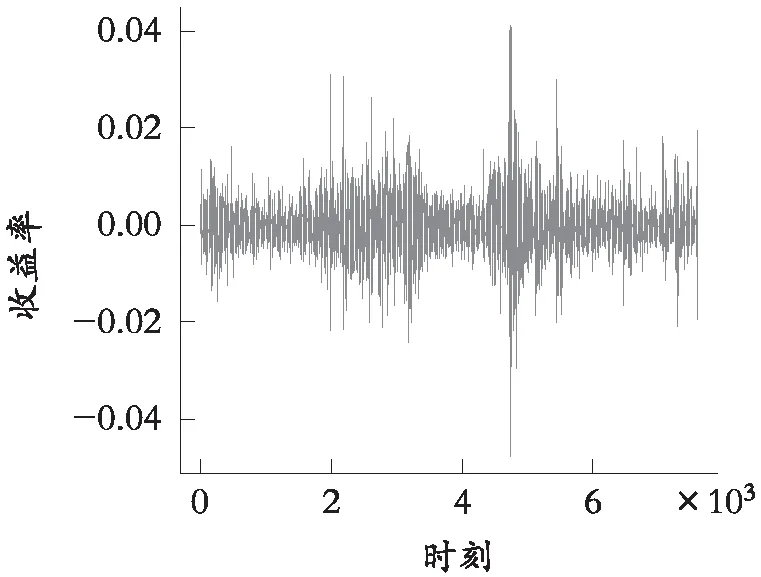
图1 标普500收益率时序图

表1 收益率的描述性统计量表

表2是EGARCH模型拟合收益率的AIC值和BIC值汇总表，根据AIC 值和BIC值越小拟合模型越优的原则，应选用EGARCH(1,1)模型对收益率进行拟合，收益率的EGARCH(1,1)模型为

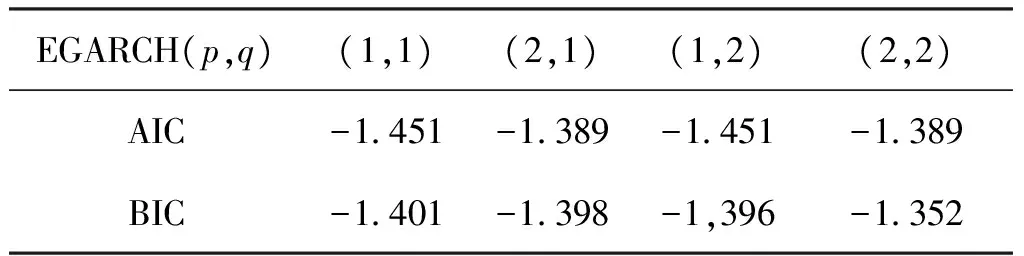
表2 EGARCH模型AIC值和BIC值汇总表

Xt=0.003 3+at,at=htεt,εt～N(0,1)

表3是EGARCH(1,1)模型检验结果表，其中Ljung-Box统计量显示EGARCH(1,1)模型拟合收益率后的标准化残差和标准化残差的平方没有显著的自相关，所以收益率拟合的EGARCH(1,1)模型是充分的。

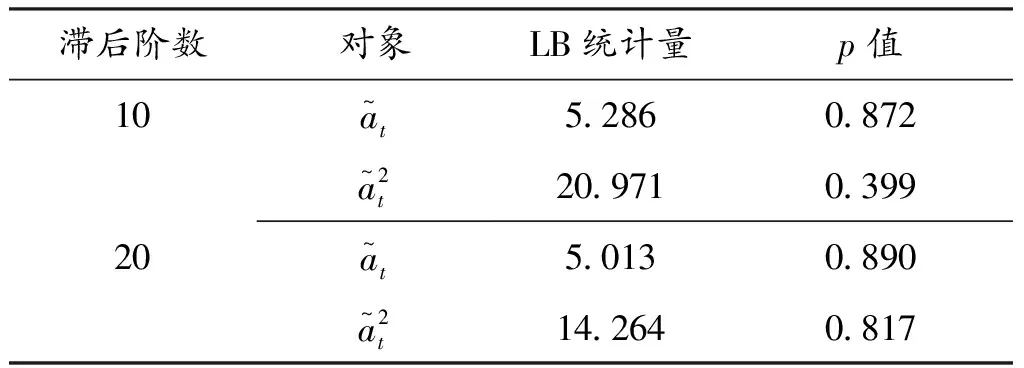
表3 EGARCH(1,1)模型检验结果表

基于3种方法(即VaRGARCH-CF方法、VaRBS方法、VaREVT方法)对VaR进行度量,选取临近2020年3月31日的255个收益率数据作为测试集，应用失败率法对3种VaR度量方法进行比较。失败率检验法是评估风险模型常用的统计检验法。该方法把实际损失超过VaR的情况记为失败，假定样本观察周期为T，p为失败率(p=T/N)，期望失败率为c(c=1-α,α为置信水平)，p与c越接近表示VaR度量效果越优[13]。表4是不同置信水平下VaR度量结果，该表给出了收益率序列在3种VaR度量方法和3个置信水平下的VaR值。由表4可知：VaR值随着置信水平α的增加而增加，因此风险厌恶者可选择较高的置信水平从而有效地度量VaR值。从失败率来看：当置信水平α=0.99时VaRBS方法对收益率序列的VaR度量效果最优，当置信水平α为0.9和0.95时，VaRGARCH-CF方法对收益率序列的VaR度量效果要优于其他两种方法。

表4 不同置信水平下VaR度量结果

4 总 结

选取的标普500指数收益率具有非对称效应和波动聚集的特征。VaRGARCH-CF方法能够较好地描述这些特征从而更好地度量VaR。研究结果表明：置信水平为0.95和0.90时，VaRGARCH-CF方法对标普500指数收益率的VaR度量效果要优于VaRBS方法和VaREVT方法。对于具有非对称效应的收益率，可考虑VaRGARCH-CF方法对其VaR值进行度量。

参考文献(References):

[1] 黎子良, 邢海鹏, 姚佩佩.金融市场中的统计模型和方法[M].北京：高等教育出版社, 2009

LI Z L, XING H P, YAO P P.Statistical Models and Methods in Financial Markets[M].Beijing: Higher Education Publisher, 2009(in Chinese)

[2] 曹志鹏, 路华.基于GARCH-VaR方法的套期保值比率与效率的实证[J].统计与决策, 2018,34(16):157—160

CAO Z P, LU H.Empirical Study on Hedging Ratio and Efficiency Based on GARCH-VaR Method[J].Statistics and Decision, 2018,34(16): 157—160(in Chinese)

[3] 于孝建, 王秀花.基于混频已实现GARCH模型的波动预测与VaR度量[J].统计研究, 2018, 35(1):104—116

YU X J, WANG X H.Volatility Prediction and VaR Measurement Based on Hybrid Realized GARCH Model[J].Statistical Research, 2018, 35(1): 104—116(in Chinese)

[4] 黄崇珍, 曹奇.基于GARCH-VaR模型的开放式基金风险度量[J].统计与决策, 2017(1):152—155

HUANG C Z, CAO Q.Risk Measurement of Open End Funds Based on GARCH-VaR Model[J].Statistics and Decision, 2017(1): 152—155(in Chinese)

[5] LU X F, LAI K K, LIANG L.Portfolio Value-at-Risk Estimation in Energy Futures Markets with Time-Varying Copula-GARCH Model[J].Annals of Operations Research, 2014(1): 333—357

[6] 魏正元,李素平, 李乔, 等.Cornish-Fisher展开在VaR中的应用[J].重庆理工大学学报(自然科学版), 2019, 33(8):232—236

WEI Z Y, LI S P, LI Q, et al.The Application of Cornish Fisher Expansion in VaR[J].Journal of Chongqing University of Technology(Natural Science Edction), 2019, 33(8): 232—236(in Chinese)

[7] 梁媛, 高彩霞.基于极值理论的ARMA-GARCH-M类模型及实证分析[J].内蒙古大学学报(自然版), 2018, 49(3):240—245

LIANG Y, GAO C X.Arma-Garch-M Model and Empirical Analysis Based on Extreme Value Theory[J].Journal of Inner Mongolia University(Natural Science Edction), 2018, 49(3): 240—245(in Chinese)

[8] SWENSEN A R.A Bootstrap Algorithm for Testing Cointegration Rank in VaR Models in The Presence of Stationary Variables[J].Journal of Econometrics, 2011, 165(2):152—162

[9] CHRISTIAN F, JEAN M Z.GARCH Models: Structure, Statistical Inference and Financial Applications[M].New York: Wiley, 2010:246—248

[10] CRAMER H.On The History of Certain Expansions Used in Mathematical Statistics[J].Biomerika, 1972,59(1):205—207

[11] VIVIANA F.Extreme Value Theory and Value at Risk[J].Revista de Analisis Economico, 2003, 18(1):57—85

[12] TURAN G B, PANAYIOTIS T.Risk Measurement Performance of Alternative Distribution Functions[J].Journal of Risk & Insurance, 2008, 75(2):411—437

[13] KUPIEC P H.Techniques for Verifying the Accuracy of Risk Measurement Models[J].Finance & Economics Discussion, 1995, 3(2):73—84