基于晶体塑性不均匀变形分析的Q235钢疲劳寿命规律预测
2021-04-13覃达威朱建文岑成贤陆大敏李泽深张克实
覃达威, 朱建文,岑成贤,陆大敏,李泽深,张克实*,4
(1.广西大学 土木建筑工程学院, 广西 南宁 530004;2.加利福尼亚大学 土木与环境工程学院, 加州 洛杉矶 90095-1593;3.绍兴文理学院 土木工程学院, 浙江 绍兴 312000;4.南宁学院 土木与建筑工程学院, 广西 南宁 530200)
0 引言
很多情形下工程结构的失效是因为其中金属承力构件的疲劳破坏所致,而金属疲劳与其服役条件下微结构演化紧密相关。PAYNE等[1]在铝合金7075的循环试验中发现疲劳裂纹的萌生与局部应变不均匀性有关,而局部应变不均匀性又与材料的细观不均匀性有关。CHAN等[2-3]通过大量试验和数值模拟发现,材料微结构在疲劳裂纹的萌生和发展上起着重要的作用,晶粒尺度的不均匀性会强烈地影响材料的疲劳寿命。SANGID[4]从试验观测和数值模拟研究了材料结构及其演化与疲劳破坏的关联,并提出应变局部集中是疲劳裂纹源的结论。
对于探讨金属或合金往复变形和疲劳的数值模拟,可在材料本构模型描述中引入晶粒取向、滑移系等细观结构信息,例如采用晶体塑性理论。BENNETT[4]用晶体塑性二维模型来模拟晶体中的循环塑性变形,在此基础上研究裂纹扩展与内部结构不均匀的关系。SWEENEY等[5]在对铁素体钢的研究中,根据试验观测的结果取有效塑性应变的循环增长率作为预测裂纹萌生的指标,然后结合晶体塑性有限元方法加以验证。ZHANG等[6-7]用晶体塑性模型结合VORONOI集合体建立材料的三维统计代表性单元,通过数值模拟低周循环试验过程材料细观变形的演变,揭示了金属材料内部不均匀变形与疲劳寿命之间的关系。郑战光等[8]则对多晶体有限元的建模作了进一步探讨。
为在文献[6-7]基础上开展更深入的研究,本文用Q235钢材料试样进行系列轴向拉压对称应变疲劳试验,得到材料在不同应变幅循环下试验的滞回曲线及疲劳寿命数据。利用多晶代表性单元(RVE)材料模型,描述不同晶粒因取向不同而呈现的细观尺度力学性质差异。然后用晶体塑性模型描述晶粒的材料循环塑性性质,与有限元方法结合,对RVE进行与试验相同的低周循环模拟。通过对RVE不均匀应变场的统计分析,探讨材料变形不均匀性演变与疲劳寿命的关系。在此基础上,以Q235钢为例,对目前只能通过系列试验才能确定的材料疲劳特性曲线能否预测的问题,进行了详细的分析和验证。
1 Q235结构钢单轴等应变幅低周疲劳试验
试验所用材料牌号是Q235B(产品标准:GB/T 3274—2007)。材料抗拉强度为412 MPa,延伸率为28.5 %,其主要化学成分见表1。

表1 Q235钢的化学成分表
将Q235钢板材加工成如图1所示的薄壁圆筒试样。为保证加载试样时端头能被试验机有效夹持,试样两端塞入了金属堵头(过盈配合)。为使试验中疲劳破坏尽可能发生在工作段,试样圆弧过渡段应尽量光滑,并且保证加工精度(IT8~IT7)和表面光洁度(Ra.5~Ra1.6)。

(a) 试样外观
试验采用引伸计控制应变幅加载方式,在MTS809拉扭电液伺服疲劳试验机上进行。疲劳试验的应变幅分别为0.003、0.004、0.005、0.006、0.008,加载波形为正弦波,频率为1Hz。试验测得疲劳寿命结果见表2。同时,记录下材料在不同应变幅下的滞回曲线,如图2所示。
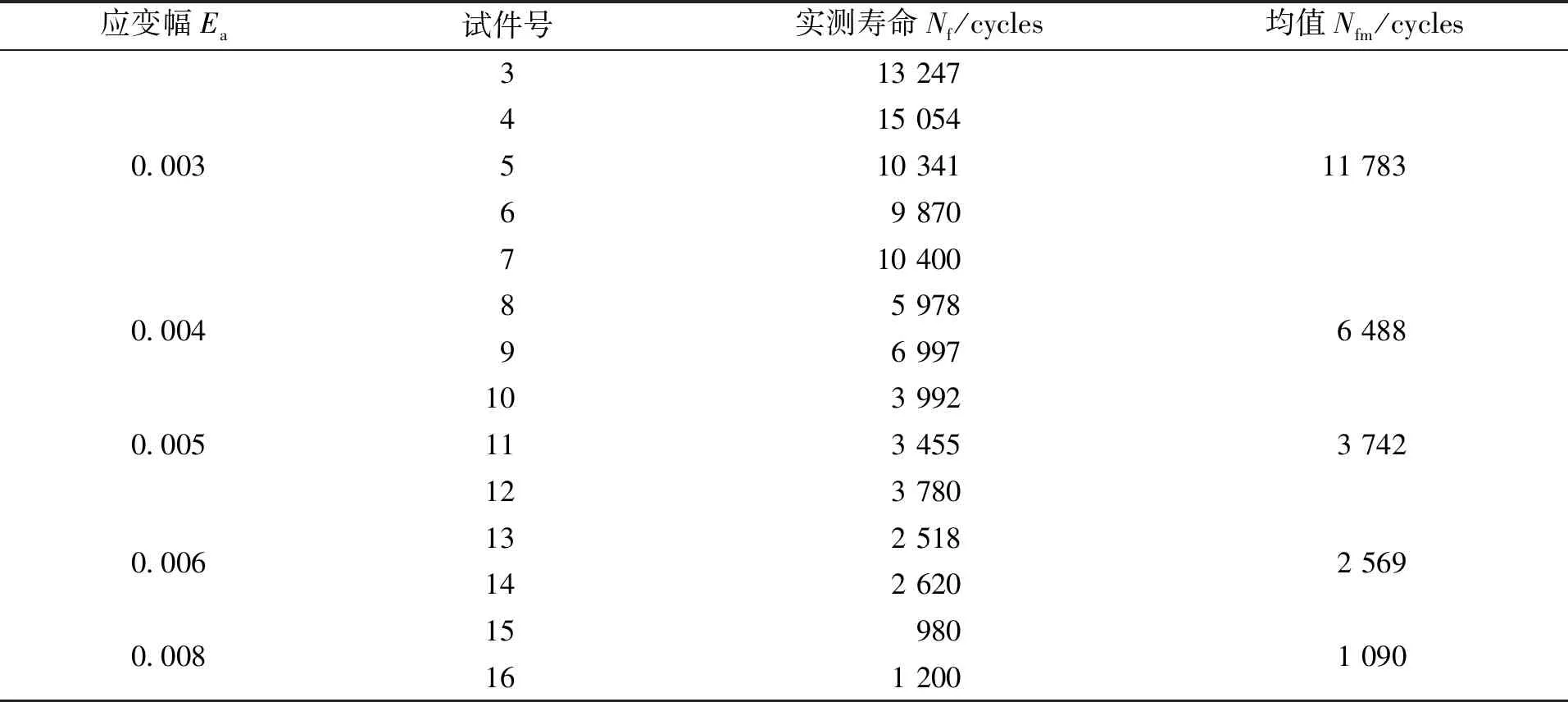
表2 Q235钢的单轴低周疲劳寿命(循环数)
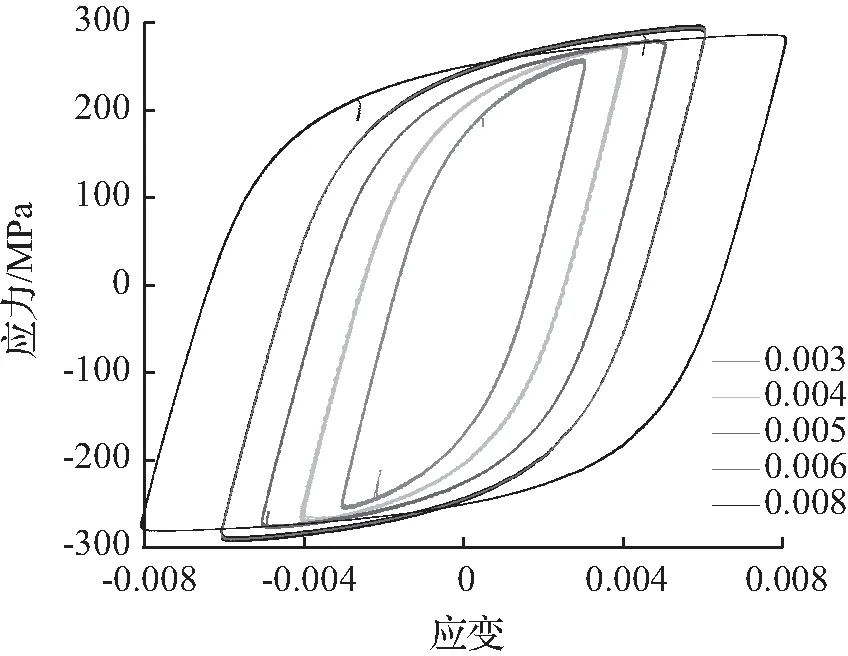
图2 试验中不同应变幅下的滞回曲线
2 晶体塑性本构模型
晶体塑性模型中,塑性变形由特定的结晶学平面的滑移确定。且滑移与晶体塑性变形梯度FP的关系为
(1)

(2)
式中:P(α)=(m(α)n(α)+n(α)m(α))/2是当前构型下的Schmid指向张量,Δγ(α)为第α滑移系的增量分解剪应变。
晶体各滑移系的分解剪应变率采用HUTCHINSON[9]建议的晶体滑移变形黏塑性滑移模型的描述,并加入了背应力[6],其表达式如下
(3)
式中:τ(α)是第α滑移系的分解剪应力,g(α)表征了该滑移系上τ(α)作用的弹性范围;X(α)是作用于该滑移系的背应力。g(α)的演化由下式表达:
(4)
式中
hαβ(γ)=h(γ)[q+(1-q)δαβ],
(5)
式中q为常数,且
(6)
式中τ0、τs和h0为待定的模型参数。而X(α)的演化规律采用文献[7]的建议:
(7)
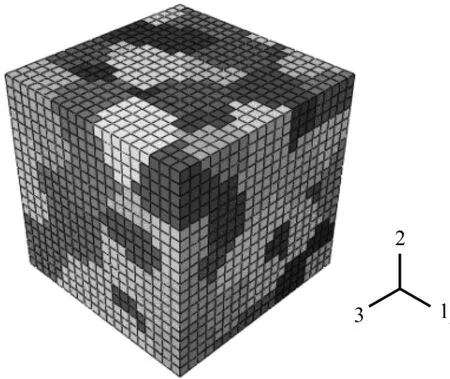
图3 Voronoi方法生成的多晶代表性单元
式中:a是描述材料应变硬化的参数;c是表征非线性硬化动态回复项的参数;e1,e2是控制背应力硬化饱和速率的材料参数。这些材料参数可通过试验拉压循环滞回曲线结合数值模拟来确定,计算采用文献[6]介绍的用于ABAQUS软件的晶体塑性材料子程序。
3 多晶代表性单元模型
用考虑材料细观结构的代表性单元(representative volume element, RVE)来描述材料的力学行为。各晶粒的空间形状按VORONOI算法生成,RVE边长为1mm,每边20等分,划分出8 000个有限元单元,组合生成126个晶粒,见图3。
RVE的边界条件:为保证连续性,模拟材料变形过程的计算对RVE施加了周期性边界条件[10-13]。该边界条件在ABAQUS软件中可通过约束方程来实施。
Q235钢的属体心立方(BCC)材料。材料晶格中有24个滑移系。为简化计算,只考虑其中的12个主滑移系,并假设每个滑移系的滑移参数都相等。该RVE模型反映了材料晶粒尺度下的非均质性,和局部变形和应力的不均匀性。当晶粒数目足够多,RVE的宏观响应近似于各向同性。在RVE上施加与实测相同的应变,参照试验以RVE整体应力应变滞回曲线与试验结果一致为目标,可标定晶体塑性材料参数,如图4所示。按此方法,并参考文献[7]中相关的晶体塑性本构方程的具体形式,最终标定的晶体塑性模型参数见表 3。

图4 试验中滞回曲线与体心立方代表性单元模拟结果的比较

表3 Q235结构钢晶体塑性模型材料参数
表3中,C11、C12、C44为弹性材料参数,其余参数为晶体塑性材料参数,见式(1)~(4)。
4 RVE循环数值模拟与材料不均匀变形的统计
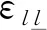
(8)

4.1 由RVE模拟分析得到应变统计标准差与疲劳寿命的关系

图5 在BCC RVE中和随循环数的变化

上述结果表明,与需要在不同应变幅值下进行大量试验,并通过拟合获得疲劳寿命曲线的传统方法比较,本文所用方法根据已知滞回行为和一个应变幅循环下的疲劳试验,就能给出该疲劳寿命曲线的近似预测。说明该方法更能合理反映材料的疲劳成因。

图6 在BCC RVE使用和的最大值、最小值和中位值所得到的预测寿命值
表4 在BCC RVE使用不同的和所得到的预测寿命值

图7 使用BCC RVE得到的预测疲劳寿命与试验疲劳寿命的对比
4.2 用FCC滑移系的RVE模型分析比较
比较晶格为面心立方(FCC)结构时的RVE分析结果。让RVE中晶粒形状、晶向及晶体塑性滑移参数不变,不同的只是各晶粒的晶体具有面心立方结构(FCC)。采用相同的方法和过程来预测Q235结构钢不同应变幅循环下的疲劳寿命,得到的结果如图8~图10和表5所示。
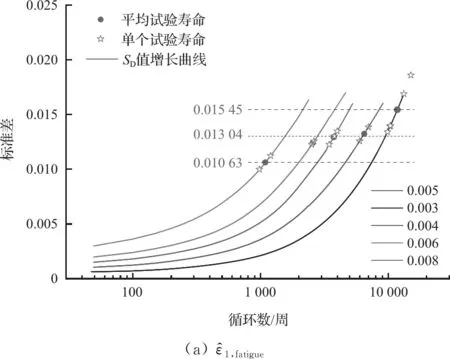
图8 在FCC RVE中和随循环数的变化。水平虚线表示和的最大值,最小值和中位值
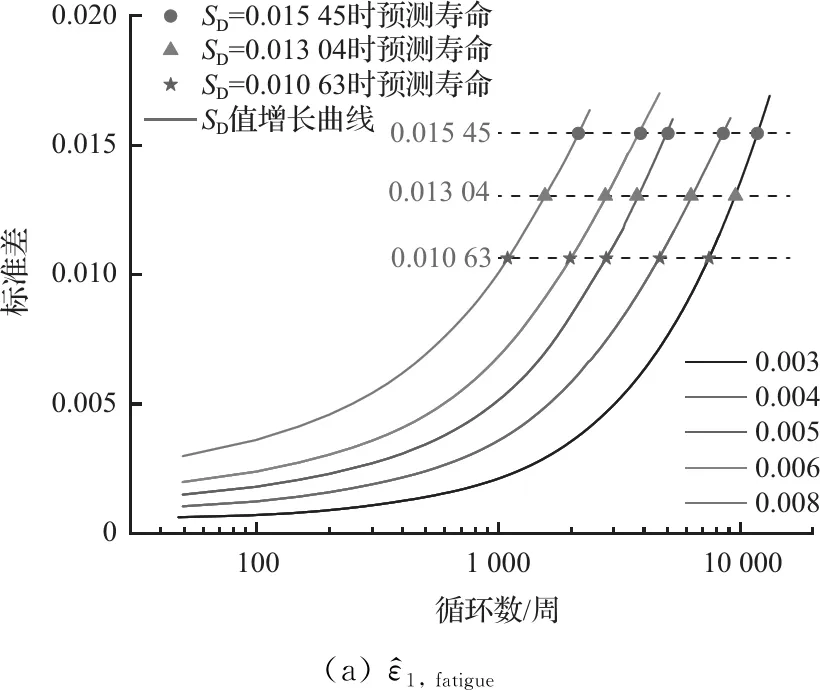
图9 在FCC RVE使用和的最大值、最小值和中位值所得到的预测寿命值

图10 使用FCC RVE得到的预测疲劳寿命与试验疲劳寿命的对比
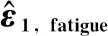
表5 在FCC RVE中使用不同的和所得到的预测寿命值
5 结论
本文研究得到以下结论:
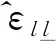
④ 本文所用方法,只利用试验取得材料循环回线及一种应变幅循环下的材料疲劳寿命,就可预测其他幅值下循环的材料疲劳寿命,从而大大减少了对经验的依赖。
