基于学情调研 重构课堂教学

王优琴

摘 要：分数是小学数学概念体系中非常重要的一个概念，分数内涵丰富，具有双重含义：“量”与“率”的含义。文章通过有针对性的学情调研，探寻第二学段分数概念学习的难点、易错点，重视分数教学中“量”的含义与分数商定义，通过别具匠心的环节设计，丰富分数的认识，扩展分数的意义，有效突破学习难点，使学习过程能够更加贴合学生的学习路径。

关键词：小学数学;学情调研;教学重构

一、现状分析与思考

（一）教学难点

人教版分数的认识教学分为两阶段：第一阶段三年级《分数的初步认识》和第二阶段五年级《分数的意义》。第一学段初步认识阶段教师们往往通过设计分一个物体、一个图形引入分数，体现分数表示部分与整体之间的关系。第二学段教师们设计《分数的意义》一课时更关注对单位“1”的理解，通过对单位“1”的等分概括分数的意义。相比三年级的《分数初步认识》，五年级《分数的意义》对分数的理解从单个物体的等分拓展到了多个物体——整体，因此教师更多地关注从一个物体到一个整体的扩张，把大量的时间投放到对单位“1”的认识与研究上，认为《分数的意义》这节课始终要落实分数的份数定义，重视分数“率”的含义，不关注分数“量”的含义，不涉及分数“商”的定义。

（二）学习难点

1. 混淆分数“率”与“量”的含义

如果给学生一条线，让学生找到1/4米有多长，很多学生想也不想直接把绳子平均分成4份，其中一份就是1/4米，将1/4米这个分数当成“率”来理解，用来刻画“部分与整体”之间的关系。

2. 学生比较难接受分数可以表示两个数相除的结果

在教学《分数与除法》这一课的前后，笔者进行了测试。前测题目：1千克的糖平均分给5位同学，每位同学分得多少千克？后测题目：3米长的绳子平均分成2段，每段长几米？不管是前测还是后测，学生遇到两数相除当结果为“分数”时，还是习惯用小数表示两数相除的结果，他们不太接受分数是个“数”，是个“结果”。

基于以上分析，发现教师预设的难点并不是学生真正的学习难点，对于真正的难点，我们关注太迟、太少。三年级《分数初步认识》所涉及的分数都是表示“率”的分数，这些知识经验给学生们积累了很强烈的信号，分数表示关系，五年级《分数的意义》教学在原有比较强的基础上再次巩固和加强，而对分数量层面的含义一直没有很好地关注，仅仅在《分数与除法》这一节课时才提及，相比较于分数“率”这部分知识的容量来说，分数“量”的教学就显得势单力薄了一点。张奠宙教授指出，小学阶段的分数定义包括份数定义、商定义和比定义，由“份数”定义到“商”的定义，是数系的扩充。这是一次跨越、一次升华，每个学生都必须面对，教师更应该重视。

二、课的实施与评价

（一）“量”“率”并进，多元多维认识分数

对于自然数的认识，首先强调自然数是一个数，然后帮助学生建立自然数也可以用来表示两个数之间的“倍数关系”。对于《分数的意义》教学，我们不仅仅关注分数“率”的含义，更应该重视分数“量”的教学，强调分数的数学本质“分数是一个数，与自然数、小数一样，是一种新的数”，并借助多种直观模型结合除法理解分数的多种含义。

【《分数的意义》教学片断一】

题目：1米长的绳子，平均分成4段，每段长多少米？

生：1÷4=0.25（米）。

师：除了用0.25表示，想一想还能用哪个数来表示呢？

师：两个数相除得到的商可以用小数表示，还可以用分数来表示。教师带来了两条绳子（0.6米与1米），你能找到1/4米吗？（出示学生不同表示方法，辨别后明确对折再对折是整条绳子的1/4，但并不都是1/4米）

设计说明：课的一开始就安排从两条不同长度的绳子里找1/4米这一活动，通过交流辩论等感知分数和小数、整数一样能表示具体的长度。

（二）重视分数商定义，丰富分数概念

著名特级教师朱乐平教师在执教《分数的初步认识》一课时，打破传统，对1/2的认识就从除法算式1÷2引入，分数的产生联系分数与除法，结合具体情境从除法的意义理解分数：1个苹果平均分给2个人，除法算式的商无法用整数表征时，学生产生了一种新的数的需求，从而自然地引出了分数，三年级的学生都能很好地接受理解，何况五年级的学生呢？他们更能深刻感悟分数因“除”而“生”，体会数系扩张，掌握分数的商定义。在执教《分数的意义》与《分数与除法的关系》对分数的认识始终应该紧密联系除法。

【《分数的意义》教学片断二】

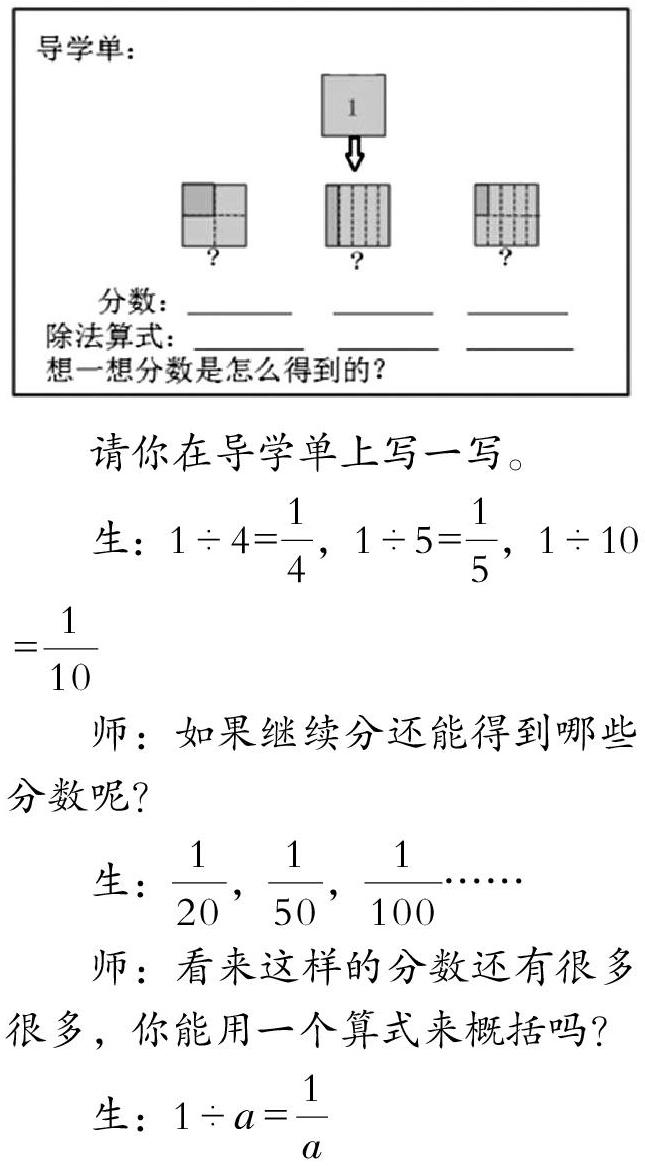
师：如果一个正方形表示1，想一想下面的阴影部分可以用哪个数来表示呢？

请你在导学单上写一写。

师：如果继续分还能得到哪些分数呢？

师：看来这样的分数还有很多很多，你能用一个算式来概括吗？

设计说明：整数有单位，分数也有单位，对于分数单位的理解，以往教师们往往都是直接告知：分子是1的分数叫做分数单位。而文中的教师通过对单位“1”的等分，结合除法引出分数单位，感悟分数单位产生的同时，感知分数与除法联系。

（三）评价结果与存在的问题

课后我们对实验班进行了后测，并选择一个班级作为对比班，题目1：把一条3dm长的绳子分成同样长的4段，每段长（ ）dm，每段是这根绳子的（ ）。题目2：一个3m2的花坛，种4种花，每种花平均占地多少平方米？

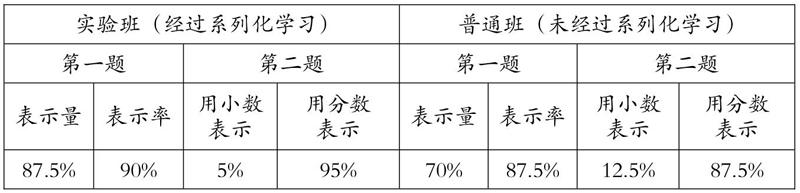
下表为检测具体结果。

检测结果发现实验班的学生，他们对分数的双重含义区分能力比普通班的学生高，尤其是对于分数表示“量”的含义，正确率明显高于普通班，对于分数表示两数相除的结果从检测的数据来看虽然实验班和普通班没有特别大的提升，但是实验班的学生对于分数与除法的关系理解更到位。然而，学生在学习《分数与除法》这一课時，也出现了一些困难，教材通过1÷3=1/3和3÷4=3/4得出分数与除法的关系，因为考虑到两数相除不仅仅指被除数小于除数，所以在课中将3÷3、4÷3的结果也作为本节课的研究内容，但仅仅是一带而过，但很多学生表示出了很大的疑惑：怎么还有这样的分数？他们心中的分数就是比1小，这对分数与除法关系的理解存在一定的影响，笔者思考是不是可以将《真假分数》的教学安排在《分数与除法》之前？有了真假分数的基础，这节课的重点探讨分数与除法的关系，引出分数值的两个意义。

三、结语

实践表明，小学生核心素养的发展离不开数学概念的支撑。分数教学中，分数概念是分数的细胞，也是构成分数体系的基石。而深度学习是提升学生概念理解的重要途径，教师着眼于从“量”和“率”两个方面，进行分数教学课堂的深度编排与思考，以实现概念教学的科学构建，以期在探讨中能够突破学生学习分数这一大知识的难点，更好地提高学生的数学学习能力。

（浙江省宁波市奉化区莼湖街道中心小学，宁波315000）