中国城市网络结构及空间关联性
2021-04-12王耀中黄选爱
王耀中 黄选爱

摘 要:基于中国城市之间的关联特征和溢出效应,将人力资本变量纳入引力模型,运用社会网络分析和机器学习方法并依据主要节点城市的有向数据,考量城市网络结构及其关联性。结果显示:新引力模型可有效衡量样本城市的网络关联效应,金融状况、港口距离和高等教育资源丰裕度是决定城市引力流量重要原因,政府干预对城市引力流作用不明显;城市空间分布呈现明显的四级分层特征,但从人力资本对城市引力流影响看,作为中心城市的广州和深圳在网络拓扑中心的稳定性相对较弱。
关键词: 社会网络分析;网络流;引力模型;城市结构
一、引 言
目前我国城市空间联系变得非常普遍,已经超越了单纯地理学意义上的“近邻”关系,并逐步呈现出多方向的网络结构形态[1,2],究其原因,除了要素自由流动形成的关联效应外,还源于协调资源配置的区域政策[3]。这种独特的城市网络发展态势不仅降低经典的空间均衡模型的解释力,而且加大了统计实证的困难。这主要体现在以下两个方面:一方面,为扭转沿海优先发展策略引发的空间发展格局扭曲,大西部开发、东北振兴、中部崛起等一系列区域协调发展政策相继出台;另一方面,随着市场化和城市化深入推进,地区之间资本和人口流动变得更加频繁,统计某时期流动人口在不同城市就业、收入和社保等相关数据变得异常困难。2017年我国农村到城市务工的流动人口数量接近2.45亿人,他们来自全国不同地区,工作地点却主要集中在发达的沿海城市及一些中西部省会城市等[4]。近些年来,不同地方政府制定了更为严格的区域发展政策,例如北京和上海等超大城市减少住宅土地供应以限制人口规模,而其他的城市却大力吸引人口流入,上述现象让传统的计量模型解决内生性变得更加棘手。
本研究认为城市“网络流”是分析城市空间网络出发点,而城市引力则是城市网络流的核心,因此,本文一项重要工作就是验证城市引力模型分析中国城市空间网络的合理性,这里讨论城市网络结构所使用的引力模型涉及城市人均产出、人力资本、人口规模和两地高速公路距离等核心变量。传统空间计量方法分析地区经济活动的空间网络关系时,往往局限于经济地理学上的“相邻”地区,很少考虑城市“网络流”的大小和方向。事实上,中国东、中、西区域发展“相互关联”关系非常强,它们地理上并不相邻,但在经济活动互动性很强,除了落后地区企业向发达地区学习先进的公司治理结构外,还有很多来源于政府因素[3,5,6],例如官员异地交换任职。这些地区关联性使得传统空间计量方法得到的结论可能有偏误。
空间网络中有方向的关联数据也称为“网络流(network flow)”数据,Taylorp J(2010)也认为“关联数据”另一说法就是“网络流”[7]。“网络流”体现了城市关联网络的有向性,例如,长沙与湘西之间人口流动是双向的,但是从湘西流入到长沙的人口远远大于其相反方向;即便资本流动,两城市之间的流动状况也不是完全对称的。“网络流”体现了城市之间实际发生的有方向的直接关联。地区交通联系支撑了物流变动,国家間贸易关系反映了资本流的存在。当然,人口流、资本流和物流等经济活动的空间变动可以使用引力模型构建关联矩阵。新引力模型是根据城市规模、人力资本与空间距离来体现的。城市规模越大,人力资本越高,引力就越大;而两地距离越大,引力就越小。引力模型主要以“网络流”作为基本分析元素,描述不同城市间互动程度和网络关系,并在统计过程中采用图论思想描述这种“关联”[8]。之前运用网络分析方法研究了国际贸易、金融一体化的网络关系及其特征[7,9]。但是这些网络流研究很少讨论城市结构,更没有验证中国城市网络引力现象。
迄今,也有一些文献使用引力模型和社会网络方法分析区域发展和能源问题。例如,刘华军等(2015)利用中国省际能源消费数据,并采用社会网络分析原理分析能源消费空间网络结构特征时发现,由于政府与市场的双重作用,中国各地区的空间关联关系呈现复杂的网络结构,且其网络稳定性逐步增强[10,11]。目前使用“网络流”分析中国城市发展问题的研究也逐渐活跃起来,李敬等(2014)用网络方法讨论中国区域经济增长空间关联问题[2],姚永玲(2020)利用社会网络分析法和关联矩阵讨论了我国的“大城市病”和 “收缩城市”问题[12],但是他们使用VAR Granger causality衡量空间溢出效应,这个方法与已有研究的思想很相似[13,14]。
为解决当前研究的相对不足,本文将从以下几个方面进行研究。一是采用社会网络分析(SNA)方法和机器学习的方法讨论了城市空间网络引力流结构及其决定因素。二是在原引力模型中加入了人力资本权重以扩展成新引力模型(gravity models),利用产生的有向关联数据(Relation Data),经由泊松似然估计建模,讨论39个样本城市的网络引力流规律和区域经济发展趋势。三是在甄别影响城市引力流量的多种因素中,使用了机器学习的两种经典模型——岭回归和lasso估计,以数据驱动的算法来解决多重共线性和内生问题。
二、引力流数据与建模过程
(一)方法与数据
城市网络流来源于中国39个不同区位层级的典型城市①,通过这39个网络节点就会产生39×38维有向数据,可大概代表整个城市空间网络变动基本态势。传统引力模型有关理论认为,城市引力由各城市经济发展水平(人均GDP)、人口规模数和城市距离确定。考虑到我国存在特殊的区域协调政策、土地制度和人口流动现象,在原传统引力模型中加入了人力资本变量,因为人力资本越高的地区,创业创新越活跃,吸引大量人流、物流和资本流,形成集聚经济,提高地区生产效率,并依此累积循环。所以城市i到城市j引力流表示为:
不同地区经济发展速度和城市生产效率提升,与投资水平、金融发展、地理区位以及政府干预均存在很强的关联性,这里将影响地区引力流的具体指标和选取方法列在表1中。
通过复杂的技术计算,将重要指标测算和统计结果如表2所示。
(二)城市网络流及其网络结构特征
在很多网络流的建模和预测中,使用了流(flow)数据定量分析网络的结构和相关优化算法。这里记G=(V,E)表示一个网络图,由于流(flow)从起始点到终点具有方向性,所以G是一个有向图[16],图的G边称为链路(link),网络流类似origin-destination矩阵。本文所关注的是某城市作为节点i到另一城市节点j的城市网络引力流fij,此时F=[fij]称为引力流量矩阵(traffic matrix)。本文利用引力模型的式(1)的计算方式和相关观测数据,建立F=[fij]矩阵,进而建立模型,共有39个城市节点,即有39×38=1482个城市网络流量数据。
由于城市网络引力流fij是由式(1)求出的,而引力模型的验证过程中,需要将引力流数据做如下处理,即将每个fij乘以5后除以F=[fij]中的最小值,将数据转化为伪计数,记做Flowcnt,其目的是将引力流变为计数形式,产生泊松分布,以方便建立均值函数和引力模型统计推断。当节点表示城市时,这些Flowcnt计数视为城市网络图有向边的权重,利用R软件igraph函数生成可视化图2。
图2展示了利用引力模型和引力流数据得到的网络图,中国城市呈现明显的四级结构,全国性中心城市、区域性中心城市、区域性地理“中介”城市及边缘城市。北京、上海、深圳、广州无疑是中国城市网络引力最大的城市,而且处于网络最中心位置;杭州、武汉、长沙、郑州、西安是区域性网络中心位置;开封、菏泽、渭南、萍乡、衡阳、黄石是区域性地理“中介”城市;四平、阜新、齐齐哈尔、海东,昭通、钦州是边缘城市。
将人力资本差距作为权重的引力流网络图如图3所示,结果显示,产生超强网络超级中心城市为北京、上海,而其他城市网络地位不明显。尽管关于城市人力资本统计和度量不完备,但上述结果仍部分地显示人力资本对城市網络引力的重要作用。
综上,构建的城市网络引力模型fij是可行的,接下来需要进一步讨论城市区位、投融资状况以及政府干预等具体解释变量与城市网络引力流的关系。
(三)对城市引力流影响因素的估计
为了提高模型的准确度,需要尽可能全面地考虑解释变量,比如将区位因素、金融投资状况、人力资本水平和政府干预等因素都囊括进来,但严重共性问题随之而来,对此使用了机器学习的两种经典模型——岭回归和lasso估计进行处理。首先,将信贷增速、人力资本、货运量、固定资产投资和财政收支比等13个解释变量纳入回归式(2)进行拟合。
通过将式(3)(4)最小化得到回归系数估计值,使用十折交叉验证法来获得调节参数λ值(fold参数设置交叉验证为10)。对λ值进行岭回归模型拟合和lasso估计,结果如表3所示。
表3结果显示,变量中人均GDP增长速度、港口距离和信贷平均增速在不同的估计情形下,其系数较大且趋势一致。这意味着地区生产效率、地理区位和金融情况影响了城市引力流量动向,高等教育资源和交通的便捷度(用交通货运量表示)也会部分地增加城市引力流。此外,财政收支比的负系数表明长期依靠政策支持或者财政转移的地区,并不能产生更强的经济活力,同时建设用地面积增速系数也为负,说明中央政府对落后地区土地政策的照顾,并没有产生很强的实际性经济效果。
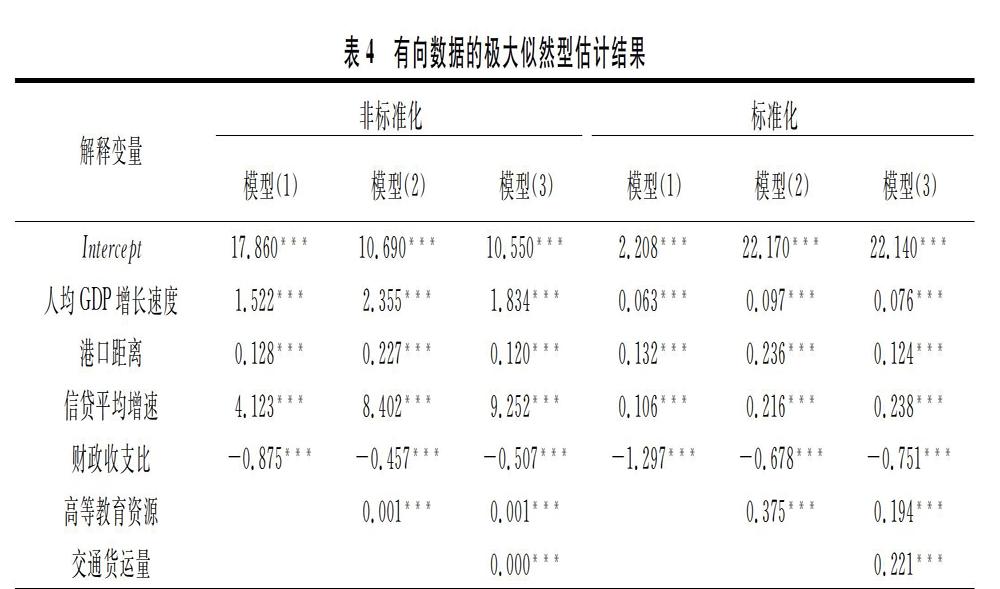
极大似然估计使用了牛顿迭代算法以获得参数渐进性正态性,将模型结果展示见表4。
模型2、模型2和模型3结果显示,独立泊松分布似然估计讨论引力流量与机器学习算法的回归结果系数正负方向基本一致,说明这39个城市样本数据中使用引力fij测算城市网络流量是合理的,唯一的差别是交通运输条件(以交通货运量衡量)系数结果显示为0,但经过数据标准化处理后,系数变为0.221。另一项重要发现是,经过标准处理后,高等教育资源(高校学生在城市人口中占比)系数变得很大,对城市引力产生巨大推动作用,这间接说明了人力资本存量相对较大的地区会增加其城市引力流。金融投资状况(信贷平均增速)和城市区位(港口距离)是影响城市引力流向的指向标,长期依赖财政转移支付的落后地区城市引力流入量并不高。
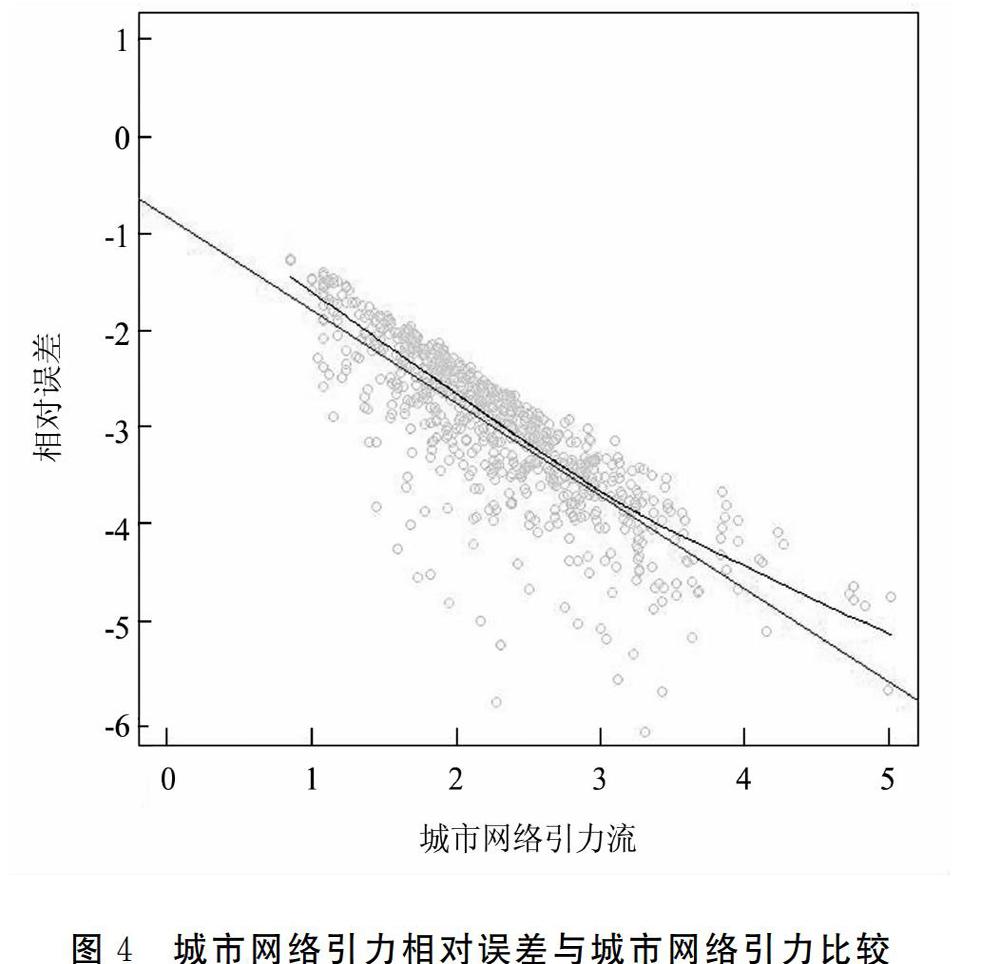
为进一步地讨论泊松似然估计模型与原引力模型的差距,本文使用R语言基本扩展包中glm函数拟合E(fij)估计值,记为,将相对误差(fij-ij)/fij与原城市引力流fij进行比较,结果如图4所示。
比较结果显示,相对误差随着城市网络引力增加而减少。两城市人流、物流和资金流互动越频繁,市场开放度越高,引力模型测算越准确。
三、结 论
本文基于城市引力流视角重新审视我国空间网络关联性及城市结构特征,尤其采用修正的引力模型和社会网络方法(SNA)检验不同层级城市引力流特征,经由机器学习方法克服内生性和多重共线性难题后,得到良好的实证效果,其主要研究发现如下:
(1)构建的城市引力模型能有效适用于39个样本城市的网络引力流分析,随着两地区人流、物流和资金流活跃程度提高,引力模型测算越准确。这个修正的城市引力模型包含三个主要变量,即城市人均产出、高速公路距离和城市人力资本状况。
(2)中国城市呈现明显的四级结构,即全国中心城市、区域中心城市、区域性地理“中介”城市及边缘城市。北京、上海、深圳、广州无疑是中国城市网络引力最大的城市,而且处于网络最中心位置,从人力资本流视角看,北京和上海在全国性区域中心位置更突出;杭州、武汉、长沙、郑州、西安是区域性网络中心位置;开封、菏泽、渭南、萍乡、衡阳、黄石等是区域性地理“中介”城市;四平、阜新、齐齐哈尔、海东,昭通、钦州等是边缘城市。
(3)金融状况和地理区位(港口距离)是引起样本城市流量变动的两个主要因素,而过度转移支付或者强政府干预对城市引力流并没有太大效果。以高等教育资源(高校学生在城市人口占比)对城市引力产生巨大推动作用来看,人力资本存量较高的地方会增加决定城市引力流。
通过样本数据分析整体网络特征看,尽管空间关联网络的连通效果比较好,但是并没有发现网络效率与城市引力流关联证据。此外,网络中心性指标(点中心度,中介中心度和接近中心度)也是值得进一步讨论的问题。
注释:
① 由于有向数据的图论分析及计量过程十分繁琐,且并不能产生更多的经济学含义,所以本文按照四大区域板块和人均GDP数量级别选取。这39座不同类型的城市为:北京、邢台、长治、赤峰、阜新、四平、齐齐哈尔、上海、盐城、宿迁、杭州、丽水、淮南、莆田、萍乡、菏泽、郑州、开封、武汉、黄石、长沙、衡阳、永州、广州、韶关、深圳、汕头、南宁、钦州、成都、泸州、遵义、昆明、昭通、西安、渭南、兰州、天水、海东。
参考文献:
[1] 胡尊国,王耀中,尹国君. 选择、集聚与城市生产率差异[J].经济评论,2017(2):3-15.
[2] 李敬, 陈澍.中国区域经济增长的空间关联及其解释——基于网络分析方法 [J].经济研究,2014(11):4-16.
[3] 刘华军,刘传明, 孙亚男.中国能源消费的空间关联网络结构特征及其效应研究[J].中国工业经济,2015(5):83-94.
[4] 潘文卿.中国的区域关联与经济增长的空间溢出效應[J].经济研究,2012(1): 54-65.
[5] 魏后凯.中国城镇化进程中两极化倾向与规模格局重构[J], 中国工业经济, 2014a(3):18-30.
[6] 魏后凯.中国城市行政等级与规模增长[J],城市与环境研究,2014b(1): 4-17.
[7] 魏守华, 杨阳, 陈珑隆. 城市等级、人口增长差异与城镇体系演变[J],中国工业经济,2020(7): 5-23.
[8] Borgatti S P,Mehra A, Brass D J. Network analysis in the social science [J]. Science, 2009,5916 (323):892-895.
[9] Eric D.Kolaczy,Gábor Csárdi. Statistical analysis of network data with R[M]. Springer,2014.
[10]Fagiolog. The international-trade network: Gravity equations and topological properties [J]. Journal of Economic Interaction and Coordination, 2010,5(1): 1-25.
[11]Milo R, Shen-Orr S, Itzkovitz S. Network motifs: Simple building blocks of complex networks[J], Science,2002,298(5594): 824-827.
[12]Oliveiram, Gamaj. An overview of social network analysis [J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery,2012,2(2): 99-115.
[13]Scott J. Social network analysis:A handbook[M]. California: Sage,2017.
[14] Taylorp J.External urban relational process: Introducing central flow theory to complement central place theory [J]. Urban Studies,2010,47(13): 2803-2818.
[15]Wasserman S, Faust K. Social network analysis: Methods and applications [M]. Cambridge:Cambridge University Press,1994.
(责任编辑:钟 瑶)
