一类高阶欧拉方程的通解

邓瑞娟，陈倩倩

（芜湖职业技术学院基础部，安徽芜湖 241003）

变系数微分方程在生物学、电学、动力学等领域都有着广泛的应用，其中形如

的微分方程被称为欧拉方程，是变系数微分方程中应用最为广泛的类型之一，受到了很多学者的关注[1-5]。如王慧等[1]就研究了二阶变系数线性微分方程何时可以转变为欧拉方程，常秀芳[2]研究了齐次欧拉方程的通解。

但因为欧拉方程的系数不是常数，非齐次欧拉方程的求解较为困难，获得的成果也较少。本文用变量代换的方法研究一类特殊的高阶欧拉方程。若记，该类方程表达式为

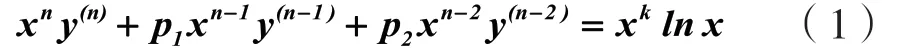
1 二阶方程

表1 齐次方程（4）的通解

2 三阶欧拉方程

表2 齐次方程（8）的通解

3 n阶方程（n≥3）