扭曲向列相液晶太赫兹相位调制器特性研究
2021-04-10乌日娜宋云鹤卢佳琦
高 芮, 乌日娜, 宋云鹤, 卢佳琦, 岱 钦
(沈阳理工大学 理学院,辽宁 沈阳 110159)
1 引 言
太赫兹波(THz)是振荡频率范围为0.1~10 THz的电磁波,在电磁频谱的微波和红外区域之间架起了桥梁,在过去20年里引起了越来越多的关注[1-4]。近年来,随着固体飞秒激光以及有效的光谱表征技术(如太赫兹时域光谱技术,THz-TDS)的发展,THz技术在传感、成像、光谱、安全检查和通信方面展现出巨大的优势和应用前景[5-7]。然而,这样成熟的THz技术不仅需要高效、廉价、紧凑的THz源和探测器,而且需要各种调制器件来引导和操纵THz波[8-9]。为了满足THz应用系统的需求,需要研发出高性能、可调控的THz相位调制器。
可调谐THz调制器可以通过不同的工艺和材料实现[10]。液晶是优异的可调控光电功能材料[11],它的介电各向异性覆盖从紫外到微波的广阔频段,具有双折射效应,在外加电场或磁场的作用下,液晶分子可以重新定向,双折射随之改变,可实现动态可调控性[12-13]。与可见光区域相比,THz波长较长,因此需要更大的器件厚度,但液晶层厚度的增加使液晶分子排列困难,这意味着响应时间较慢,损耗更高。如果液晶的双折射率较高,则可以使用较薄的液晶层来获得相同的相移,从而降低损耗。目前有一些在可见光波段不常见的液晶材料在THz波段表现出较好的双折射特性[7,14-15],如LCMS107 (ne:1.80~1.85,no:1.50~1.62)、BNHR (ne:1.860~1.883,no:1.581~1.602)和 LC1825 (ne:1.91~1.95,no:1.54~ 1.57)。
目前THz液晶移相器有多种调控方式,如温控、磁控、电控等,其中电控方式比较方便,降低器件成本,具有较好的应用前景。2004年,Cho[16]等人在实验中利用177 V的电压驱动厚度为38.6 μm的液晶在1.07 THz处获得4.07°的相移。两年后他们进一步用厚度为570 μm的E7液晶在1THz处实现了93.7°的最大相移,驱动电压为125 V[17]。2013年,Wu[18]等人提出了一种以石墨烯薄膜作为透明电极的液晶THz移相器。在50 μm厚的液晶盒中,最大相移为10.8°,饱和电压为5 V。2017年Chodorow[19]等人提出了基于胆甾相液晶(ChLC)的THz移相器,液晶层厚度为454 μm,在2.5 THz处相移约为π。
液晶分子扭曲取向相比于平行取向具有响应时间较快、透光性能对波长和入射角的依赖性小等优点,因此本文分别设计了透射型和反射型扭曲向列相液晶相位调制器,采用传输矩阵理论数值模拟了0.2~1.2 THz范围内的相位调制特性,分析了器件不同的扭曲角对相位调制特性的影响。
2 液晶的相位调制理论
液晶是介于固态与液态之间的一种中间状态,由于液晶分子的排列类似于晶体,有一定的规律,所以表现出很强的光学各向异性和介电各向异性。将液晶层的上下两个基板做适当的取向处理,使液晶分子在两基板处都是沿基板表面平行排列,但它们的长轴方向相差90°,即上下两基板表面的液晶分子指向矢相互垂直,从而形成90°扭曲排列方式[20]。将基板间的液晶层进一步分成许多薄层,每一层内分子的取向基本一致,且平行于层面,相邻层分子的取向逐渐转过一个角度,这样可以将每个薄层的液晶看作是一个单轴晶体[21]。图1(a)是90°扭曲排列液晶示意图,z轴方向为液晶层的方向,此时是不加电场的状态。当沿着z轴方向加电场时,在不考虑液晶基板表面的锚定作用下,所有的液晶分子都朝着电场方向转动产生一个倾角θ(液晶分子长轴与x轴的夹角),倾角θ随着所加电压增大而增大,且是电压的均方根函数[22],电压足够大时,液晶分子的长轴会沿着电场方向(z轴)排列,如图1(b)所示。

(a) 外加电压为零(a)Applied voltage is zero

(b) 外加电压大于阈值电压(b) Applied voltage is greater than the threshold voltage图1 扭曲排列液晶示意图Fig.1 Schematic diagram of twisted liquid crystal
检验偏振光沿扭曲向列相液晶器件的扭曲轴(z轴)传播后输出光状态的最简单方法是用琼斯矩阵[23-27]进行分析。如前文所述,把厚度为d的整个液晶层沿z轴分成均匀的N个薄层,液晶分子长轴在z=0处与x轴对齐,每一层的液晶分子相对于前一层转过同一角度,则每一层中液晶分子的扭曲角可用下式表示:
Δχ=α/N
(1)
其中:α为液晶盒的总扭曲角。考虑到各液晶层的连续性,推得第n层的扭曲角为:
χn=nΔχ=nα/N
(2)

(3)
其中:
(4)
每一层液晶对光的作用相当于一个相位延迟片,光波经过第n层液晶的琼斯矩阵变为:

(5)

其中:
(6)
并且β=πd[ne(θ)-no]/λ是液晶材料的双折射,φ=πd[ne(θ)+no]/λ=φ0+β,λ为入射光的波长,ne(θ)为液晶的有效折射率,根据各向异性介质的折射率椭球公式:
(7)
将式(5)旋转回原坐标系得到:

(8)
其中:Jn为第n层液晶的琼斯矩阵,液晶总的琼斯矩阵是单个矩阵的乘积。经过处理得到液晶的琼斯矩阵为:

(9)


3 透射型相位调制器
液晶盒通常放在起偏器和检偏器之间,在图2所示的结构中,设它们的偏振方向与x轴的夹角分别为φ1和φ2,液晶层前表面分子取向与x轴平行,液晶盒扭曲角为α。那么经过起偏器、液晶盒、检偏器的输出光的琼斯矩阵可表示为:
Eout=P2×J×E0
(10)


图2 透射型相位调制器结构图Fig.2 Structure diagram of transmissive phase modulator


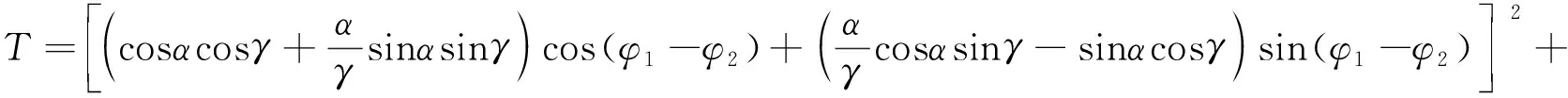
(11)
(12)
根据图2装置模拟THz波段电控可调谐透射型液晶相位调制器。选用正性液晶混合物LC1825,其各向异性参数为:ne=1.93,no=1.56,Δn=0.37,ε‖=3.72,ε⊥=2.43。拟定液晶盒的厚度是250 μm。图3是依据公式(11)和(12)得出的输出光透过率和相位延迟随液晶双折射β的变化关系曲线。需要注意的是,根据公式(12)所得到的相位延迟是正切的反函数,计算时会出现π相位的跳变,在模拟时要注意π补偿的问题。另外,90°扭曲(0,0)相位延迟曲线在透过率T=0的地方仍存在跳变。
图中(0,0)和(0,90)表示起偏器、检偏器的偏振角φ1和φ2分别为0°、0°和0°、90°。根据模拟所选的器件参数和频率范围(0.2~1.2 THz)计算得到液晶双折射β对应的取值为0°~66.7°,在此范围内透过率的变化情况为:(0,0)情况下扭曲角为30°、45°和90°所对应的透过率变化为1~0.77,1~0.59,1~0.56;(0,90)情况下扭曲角为30°、45°和90°所对应的透过率变化为0~0.44,0~0.41,0~0.23。图3(b)可以看出(0,0)情况下90°扭曲相位延迟曲线的斜率为1,而30°和45°扭曲相位延迟曲线是斜率为2的直线,相对来说30°和45°扭曲比90°扭曲能获得更大的相位调制。
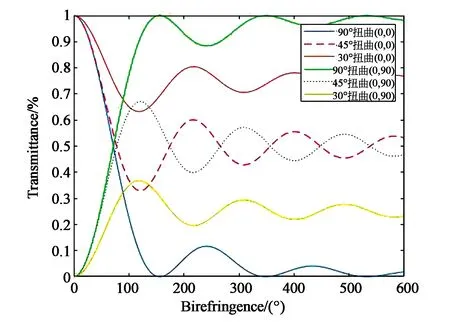
(a)透过率T与双折射β的关系(a)Relationship between transmittance T and birefringence β

(b) 相位延迟δ与双折射β的关系(b)Relationship between phase retardation δ and birefringence β图3 透过率和相位延迟随双折射的变化关系Fig.3 Transmittance and phase retardation change with birefringence
将起偏器与检偏器平行放置,且与液晶层前表面的液晶分子平行。将液晶盒上下两个基板的取向方向设置为30°、45°、90°,获得不同的扭曲角,得到透过率和相位延迟随频率变化的曲线,如图4所示。

(a)透过率曲线(a)Transmittance curves

(b)相位延迟曲线(b)Phase retardation curves图4 不同扭曲角的调制曲线Fig.4 Modulation curves of different twist angles
图4(a)中,随着频率增大,30°、45°和90°扭曲的透过率从0.99左右分别下降到0.77、0.59和0.56。由于液晶的双折射效应和偏振片的共同作用造成透过率T变化,根据公式(11),当扭曲角α、偏振器的偏振角φ1和φ2确定后,T只与β有关(γ是β的函数),又因β=πd[ne(θ)-no]/λ,THz范围内随着频率增大,波长变小,使双折射β增大,结合图3(a)可知导致透过率下降。相同频率下45°和90°扭曲所得的透过率变化大致相同,30°扭曲得到的透过率高且变化范围较小。图4(b)中,随着频率增大,液晶双折射β变大,进而相位延迟增大,频率为1.2 THz时分别可达到126°、115°和67°,即30°和45°扭曲的相位延迟相近,且远大于90°扭曲的相位延迟。由此可以看出,当相位延迟量相同的情况下,30°扭曲会比45°扭曲对光的利用率更大一些,减少了损耗。因此选择扭曲角为30°进一步分析电压效应。由于液晶分子的倾角θ是电压的函数,在图1原理图中,加电压液晶分子倾角变大,因此可以通过倾角的变化看出电压效应。将θ值分别取值为0°、30°、45°、60°和80°,得到不同倾角下透过率曲线和相位延迟曲线如图5所示。

(a) 透过率随频率的变化关系(a)Relationship between transmittance and frequency
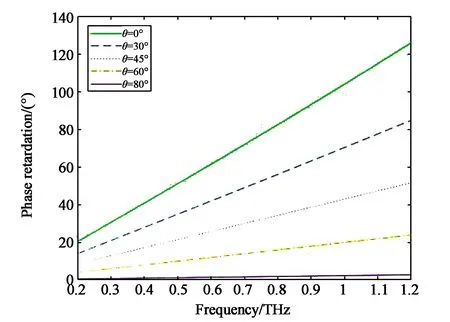
(b)相位延迟随频率的变化关系(b)Relationship between phase retardation and frequency图5 不同倾角的调制曲线Fig.5 Modulation curves of different tilt angles
由图5(a)可知,相同频率下随着倾角增大透过率逐渐增大,当倾角达到80°时,透过率近似为1,这是因为倾角增大导致液晶分子不再扭曲,而是垂直于基板排列,液晶分子的旋光性消失,使得从起偏器入射的偏振光在输出时与检偏器偏振方向一致。图5(b)为不同倾角下相位延迟的变化曲线,可以看出,频率相同时,相位延迟随倾角的增大而减小,因为倾角增大有效折射率减小,导致双折射β减小。1.2 THz时,倾角为0°、30°、45°、60°和80°时的位相延迟分别为126°、85°、52°、24°和3°,可以实现相位延迟电压调谐。
4 反射型相位调制器
根据上文透射型器件的研究方法对反射型器件进行相应的分析。反射型相位调制器主要由起偏器、液晶层、基板反射镜、检偏器构成。入射光由起偏器和半透半反镜进入液晶层后,经过反射镜反射再次进入液晶层,最后在检偏器方向输出光。在THz波段金属材料相比于其他材料表现出极高的反射率,可用来做反射镜,目前THz反射镜大多都是金材料。
在图6所示的结构中,设起偏器和检偏器的偏振方向与x轴的夹角分别为φ1和φ2。那么输出光的琼斯矩阵[28-29]可表示为:
Eout=P2×R(α)×J×
R(-α)×Mi×J×E0
(13)
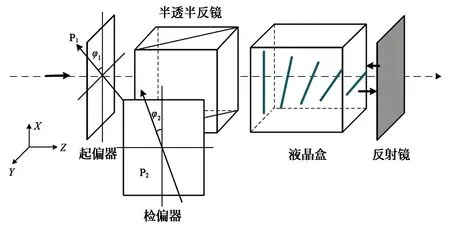
图6 反射型相位调制器结构图Fig.6 Structure diagram of reflective phase modulator


(14)
(15)

根据图6装置模拟THz波段电控可调谐反射型液晶相位调制器,液晶盒参数与透射型相同。依据公式(14)和(15)得出输出光反射率和相位延迟随液晶双折射β的变化关系曲线,如图7所示。与透射型类似,相位延迟要注意π跳变的问题。
图中(0,0)和(0,90)表示起偏器、检偏器的偏振角φ1和φ2分别为0°、0°和0°、90°。由图7(a)可知,在双折射β为0~66.7°范围内,(0,0)情况下30°、45°和90°扭曲的反射率变化为1~0.53、1~0.19和1~0.31;(0,90)情况下30°、45°和90°扭曲所对应的反射率变化为0~0.47,0~0.81,0~0.69。图7(b)可以看出(0,0)情况30°和45°扭曲的相位延迟量较大,更适合做相位调制器。因此偏振器摆放与透射型相同,模拟THz波段不同扭曲角的反射率和相位延迟随频率变化的曲线,如图8所示。

(a)反射率R与双折射β的关系(a)Relationship between reflectivity R and birefringence β

(b)相位延迟δ与双折射β的关系(b)Relationship between phase retardation δ and birefringence β图7 反射率和相位延迟随双折射的变化关系Fig.7 Transmittance and phase retardation change with birefringence

(a)反射率曲线(a)Reflectivity curves
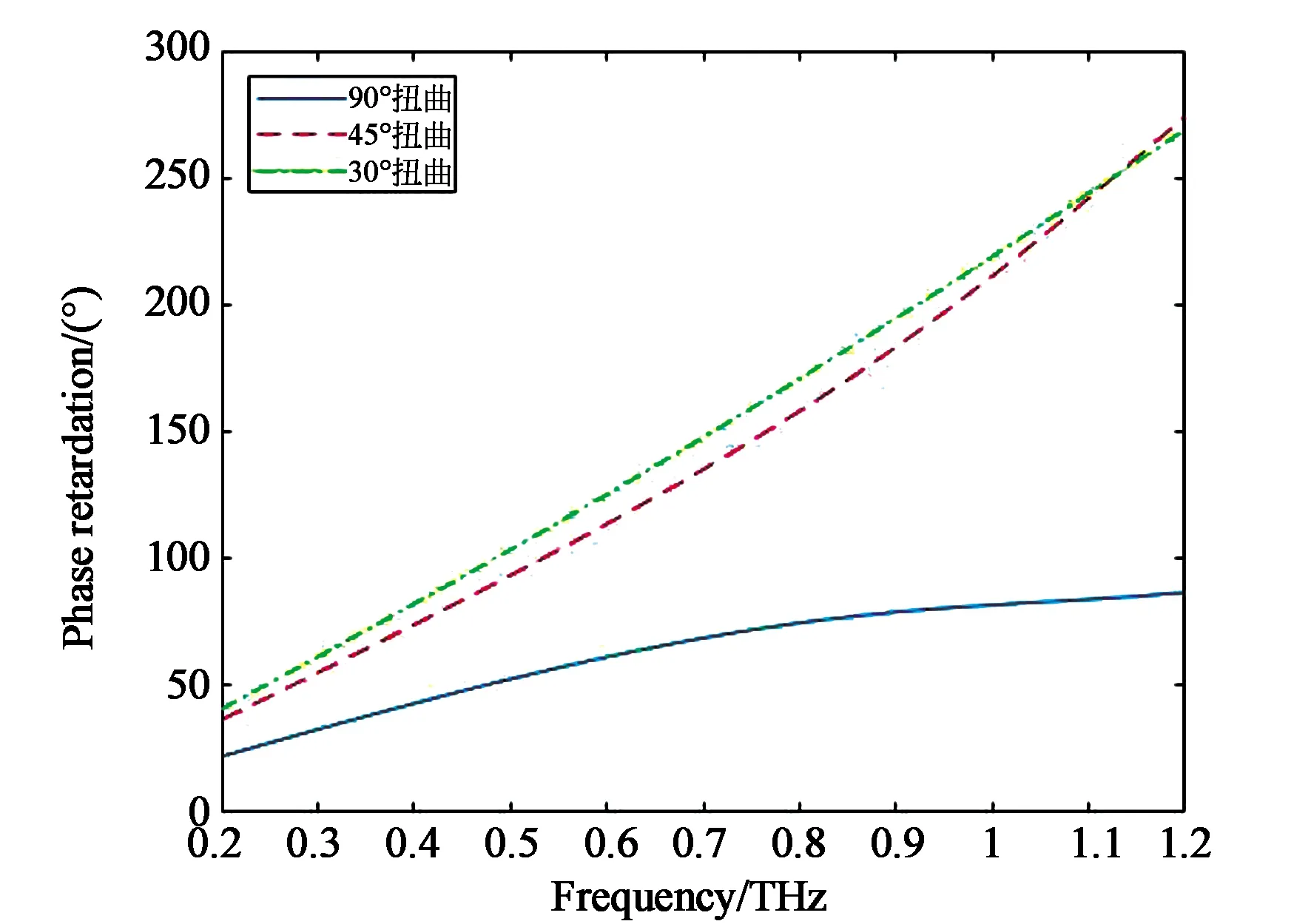
(b)相位延迟曲线(b)Phase retardation curves图8 不同扭曲角的调制曲线Fig.8 Modulation curves of different twist angles
曲线的变化趋势与透射型相似,图8(a)中45°和90°扭曲的反射率变化幅度剧烈,从0.97分别下降到0.19和0.31,对光的损耗较大,30°扭曲得到的反射率高且变化范围较小,从0.97降到0.53。图8(b)中30°和45°扭曲的相位延迟曲线相近,最大的相位延迟量达到270°,而 90°扭曲的最大相位延迟量为87°。由此可以看出,在相位延迟量相同的情况下,30°扭曲是更优的选择,这与透射型器件具有相同的结论。
图9为30°扭曲器件不同倾角的反射率和相位延迟变化曲线,倾角θ的取值与透射型器件相同。倾角为0°时在1.2 THz处的反射率为0.53,曲线的变化趋势与透射型相同,在此不做赘述。

(a)反射率随频率的变化关系(a)Relationship between reflectivity and frequency

(b)相位延迟随频率的变化关系(b)Relationship between phase retardation and frequency图9 不同倾角的调制曲线Fig.9 Modulation curves of different tilt angles
反射镜的作用使光在传输过程中经历了两次液晶层,相当于增加了一倍的有效光程,使相位延迟增大到270°。综合看来,反射型器件对光的损耗虽比透射型大,但是相位调制量大幅提高,约为透射型的2倍,验证了模拟结果的准确性。
5 结 论
本文利用琼斯矩阵理论分析THz波段偏振光在扭曲向列相液晶盒中的传播状态,探究不同扭曲角对相位调制特性的影响,综合透过率和相位延迟量两个因素来看,扭曲角越小达到的效果越好。设计透射型和反射型30°扭曲液晶相位调制器并数值分析其在0.2~1.2 THz波段的相位调制特性,通过液晶分子倾角和电压的关系分析了器件的电压效应,在1.2 THz倾角为0°、30°、45°、60°和80°时,透射型器件的位相延迟分别为126°、85°、52°、24°和3°,反射型器件的位相延迟分别为270°、176°、105°、48°和6°,即与透射型相同的厚度下,反射型获得的相位延迟约为透射型的2倍。这些分析结果对于THz波段液晶相位调制器的设计与应用具有重要的借鉴作用。
