亚微米级向列相球形液滴中分裂核结构稳定性的探究

刘宏恩， 吴金兵， 刘猛飞， 周 璇， 张志东

(河北工业大学 应用物理系，天津 300401)

1 引 言

很多技术都依赖于液晶微滴内部的分子取向[1-2]。例如在聚合物分散液晶(PDLC)系统中，液晶微滴均匀分布在聚合物网络中，无外场作用时，系统存在很高的灰度[3]；当施加外场作用时，液晶微滴的对称轴和内部液晶分子会沿着外加场作用的方向排列，此时系统呈现透明状态，由此可以制作性能良好的光控膜等光学器件。一般来说，液晶微滴内部的分子排列方式是由微滴的表面能与本体能相互作用导致的。对于向列相液晶微滴，早期大量的实验和理论研究主要针对于微米级大尺寸情况[4-7]，而近年来对于更小尺寸的研究已经逐渐成为热点问题。对于亚微米级尺寸的研究，一些团队也给出了相关介绍[8-11]。研究发现，双极结构(bipolar structure)、径向结构(radial structure)是液晶微滴中最为常见的两种结构，其中，双极结构在几微米甚至几十微米情况下都可以稳定存在。对于径向结构， 早期Schopohl和Sluckin等人[12]解释为在球中心处有一个各向同性点；Penzenstadler等人[13]通过研究提出各向同性点实质上应该是分裂后的小的+1/2缺陷环(ring)；随后Sonnet等人[14]通过模拟计算验证了Penzenstadler等人的猜想。近年来，随着科学技术不断发展，人们的研究重点逐渐趋于更小尺寸。Gupta等人在实验上能够制备出直径从700 nm到8 μm的液晶微滴[15-16]；Bacchiocchi等人进一步在一系列不同的实验中制备出直径从50 nm到300 nm的液晶微滴[17]。

Prishchepa等人通过改变边界条件(由沿面锚定条件转变为垂面锚定条件)，发现液滴中的双极结构会变为径向结构[18]。Gupta等人发现当液晶微滴直径由3 μm减小到1 μm时，双极结构会转变为预径向结构(pre-radial structure)，继续减小直径，当其约为700 nm时，变为径向结构。该现象的出现是由于随着直径减小，表面能作用相对增强，鞍形弹性常数k24(saddle-splay)项在与表面能、本体能和弹性能的相互竞争中逐渐发挥着不可或缺的作用。研究还发现，当不考虑k24项作用时，随着尺寸的逐渐减小，双极结构会转变为均匀结构[15]。对于圆柱中双扭曲结构(double-twist structure)，Davidson等人发现由于k24弹性项作用，使得边界附近指向矢更易沿曲率最大的方向排列[19]。Zumer等人[20]的研究结果表明，在球形液滴中，由于k24弹性项作用于表面上，因此很难区分k24作用和边界锚定作用，在此情况下，即使无边界锚定作用，k24也可以稳定球形液滴内部的指向矢结构，因此，此时k24作用可以部分代替边界锚定作用。

Mkaddem等人[21]在垂面强锚定条件下发现3种结构：径向结构、环结构和分裂核结构，而对于分裂核结构(split-core structure)，其总是以亚稳态的方式存在。An等人[8]分别在垂面强锚定边界条件和镜像-垂面(mirror-homeotropic)边界条件下研究了分裂核结构和-1分裂核结构。对于上述有关分裂核结构的研究结果，发现其总是以亚稳态形式存在，而这也是本文的重点研究问题。基于Landau-de Gennes理论，本文主要从弱锚定边界条件出发，通过考虑k24弹性项的作用，研究亚微米级尺寸下分裂核结构成为稳态的存在范围。

2 几何模型

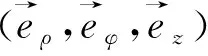
图1 球状结构示意图Fig.1 Schematic diagram of spherical structure

3 理论方法

3.1 序参数张量Q与双轴性参数β2

液晶的研究理论方法一般为Frank理论与Landau-de Gennes理论。Frank弹性理论对于描述液晶连续体更有优势；而对于存在缺陷的液晶系统，Landau-de Gennes理论既保持了棒状液晶分子的首尾不变性又能够利用双轴性来具体描述缺陷的状态，所以本文选取Landau-de Gennes理论进行研究。在主轴系中，序参数张量Q可以表示为[22]：

(1)

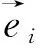
序参数张量Q为对称无迹张量，它满足Qij=Qji，trQ=0。液晶系统处于各向同性相时，Q=0，此时3个本征值都为0，液晶分子处于完全无序状态。当液晶系统中有两个本征值相等且不等于0时，此时系统为单轴态。单轴序参数张量Q表示为：

(2)

(3)

由于序参数张量Q为对称无迹张量，所以存在关系Qρφ=Qφρ，Qρz=Qzρ，Qφz=Qzφ，Qρρ+Qφφ+Qzz=0。当序参数张量Q的3个本征值互不相等时，此时液晶系统处于双轴态。利用双轴性参数β2定义双轴性：

(4)

双轴性参数β2的取值范围为[0,1]。当β2=0时，系统处于单轴态，当β2=1时，系统具有最大的双轴性。由于存在tr(Q3)=3detQ，当β2=1时，对应的detQ=0，这表明液晶系统拥有最大双轴性时，序参数张量Q的3个本征值至少有一个为0。

3.2 柱坐标系下的Landau-de Gennes理论

无外加场作用下，液晶系统中Landau-de Gennes理论的总自由能密度表示为：

F(Q)=Fbulk+Felastic

(5)

其中：Fbulk为本体自由能密度，Felastic为弹性自由能密度。对于本体自由能密度Fbulk，其只依赖序参数张量Q并不依赖坐标系的位置选取，具体形式表示为：

(6)

Felastic为液晶取向序的不均匀引起的弹性自由能密度，依赖于序参数张量Q的空间变化率，只考虑Q及其导数的二次项，Felastic具体表示为：

(7)

Li与Frank理论中的展曲弹性常数k11、扭曲弹性常数k22、弯曲弹性常数k33之间存在关系为[23]:

(8)

其中：k24是鞍形弹性常数,根据Ericksen[24]、Beris和Edwards[25]等人得出的关于Frank理论的弹性常数k11，k22，k33，k24满足的不等式：

k11≥ 0，k22≥ 0，k33≥ 0

(9)

-k22≤k24≤ min(2k11-k22,k22)

(10)

(11)

(12)

利用张量Q无迹处理和泛函的约束变分得到平衡态的欧拉方程[20]。在柱坐标系下为：

(13)

本文使用松弛迭代方法对液晶系统进行数值模拟，在此动力学方程中，序参数张量Q是时间t的函数，给定初始条件后将得到其随时间演化的平衡态结果。动力学方程如下：

(14)

其中：Γ=6D*/[1-3tr(Q2)]2，D*为系统的转动扩散系数。约化后的动力学方程为：

(15)

3.3 边界条件及参数选取

当系统不存在外场的作用下，液晶系统的边界条件会对内部液晶分子的排列方式产生重要影响。本文需要考虑液晶微滴的弱锚定边界情况，所以给出表面能密度的具体表达形式：

(16)

其中Qs为表面易取向的序参数张量，仅描述边界指向矢的空间变化，具体可表示为：

(17)

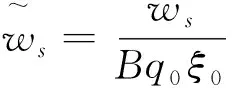
(18)

弱锚泊的边界条件方程为：

(19)

上式约化得到的方程为：

(20)

对于球形液滴可以表示为：

(21)

其中：式(21)是在柱坐标系下写出的表达形式，νρ和νz分别是沿外法线的ρ分量和z分量。

本文模拟过程中选取了液晶材料5CB[22]的各项系数：A0=0.195×106J/m3K，B=7.155×106J/m3，C=8.82×106J/m3，D*= 0.35 m2N-1s-1，引入的相干长度ξ为2.64 nm，约化温度设定为则序参数约化后为：

4 结果与讨论

4.1 强锚定下径向、环和分裂核结构

锚定条件的变化、弹性各向异性、尺寸效应、温度都会对液晶微滴内部指向矢结构的稳定性产生影响。首先我们研究当边界条件强锚定时，单一常数近似与弹性各向异性两种情况下尺寸效应对径向、环和分裂核结构的影响。根据Mkaddem等人对于径向结构内部缺陷的精细研究[21]，在强锚定、单一常数近似且温度相对较高时，存在两种结构：径向结构和环结构，并给出在尺寸很小时，只存在径向结构的相图。分别选取r=50ξ、r=150ξ的液滴进行研究。在强锚定、单一常数近似下，发现液滴内部存在两种结构：径向结构和环结构。如图2和表1所示，当半径r=50ξ时，对比能量，发现径向结构为能量最低态。

(a) 径向结构指向矢图(a)Profiles of the director of the radial configuration

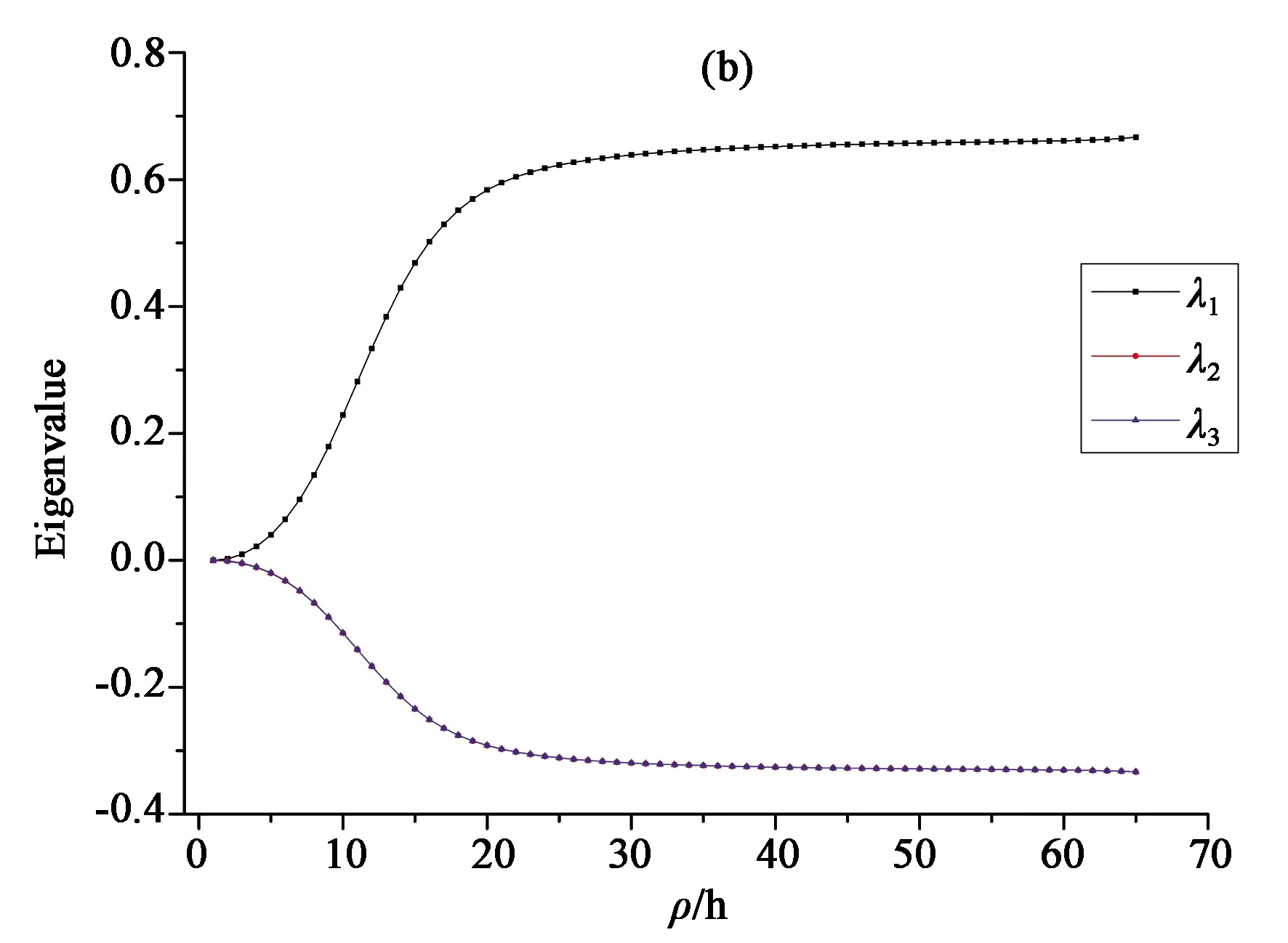
(b) 中间部分沿ρ轴的本征值，其中λ2 = λ3。(b)Eigenvalues at the center along ρ axis, λ2 = λ3.

(c) 环结构指向矢图(c) Profiles of the director of the ring configuration

(d) 中间部分沿ρ轴的本征值(d)Eigenvalues at the center along ρ axis图2 半径为50ξ时径向结构与环结构指向矢图Fig.2 Profiles of the director of the radial configuration and the ring configuration when the radius is equal to 50ξ

表1 强锚定下径向结构与环结构的能量对比Tab.1 Difference of energy between the radial structure and the ring structure under strong anchoring

图2(a)、(c)为球半截面的指向矢示意图，蓝色圆圈代表缺陷的位置分布，可以看出径向结构的缺陷位于球中心处。图2(b)是中间部分沿ρ轴的本征值图，中心处为各向同性点，此时3个本征值相同且为0。环结构最先被Penzenstadler和Trebin等人预测[4]，图2(d)是中间部分沿ρ轴的本征值图，此时环缺陷位置距中心约为16ξ。当半径r=150ξ时，对比能量，环结构为能量最低态。通过模拟发现，当r≤100ξ时，径向结构为稳态，r≥100ξ时，环结构为稳态。当半径足够小时，只存在径向结构，而环结构不再稳定，此结论与 Mkaddem等人的结论一致。

接着，我们探究了在强锚定、弹性各向异性下径向结构和环结构的结构变化。选取小半径的尺寸r=50ξ(132 nm)、r=60ξ(158 nm)、r=70ξ(185 nm)进行研究。当半径为r=50ξ、L2/L1=1.7，对应k11/k22=1.85时，径向结构不再稳定存在，而是转变为分裂核结构，因此随着k11的增大，液晶系统更难发生展曲形变，而在径向结构中展曲形变占主导作用，所以此时径向结构不再稳定存在。在弹性各向异性下会出现分裂核结构，下文将不再详细论述。根据An等人以及Mkaddem等人的研究：在强锚定、单一常数近似且温度较低的情况下，分裂核结构可以存在，但总为亚稳态[8,21]。通过计算我们发现在强锚定、弹性各向异性时分裂核结构可以存在，并在相同条件下也发现了环结构，对比能量环结构为能量最低态。图3(a)、(b)为半径r=50ξ、L2/L1=1.7的分裂核结构指向矢图和沿z轴的本征值图。根据Mkaddem等人对分裂核结构的特征描述，其内部存在一条较短的沿对称轴分布的向错线且两端端点为各向同性点，而中间部分为负序参数单轴态。如图3(b)所示，在z=64ξ和z=66ξ处，3个本征值相同且为0，因此在我们模拟得到的分裂核结构中，其内部的向错线长度为2ξ。

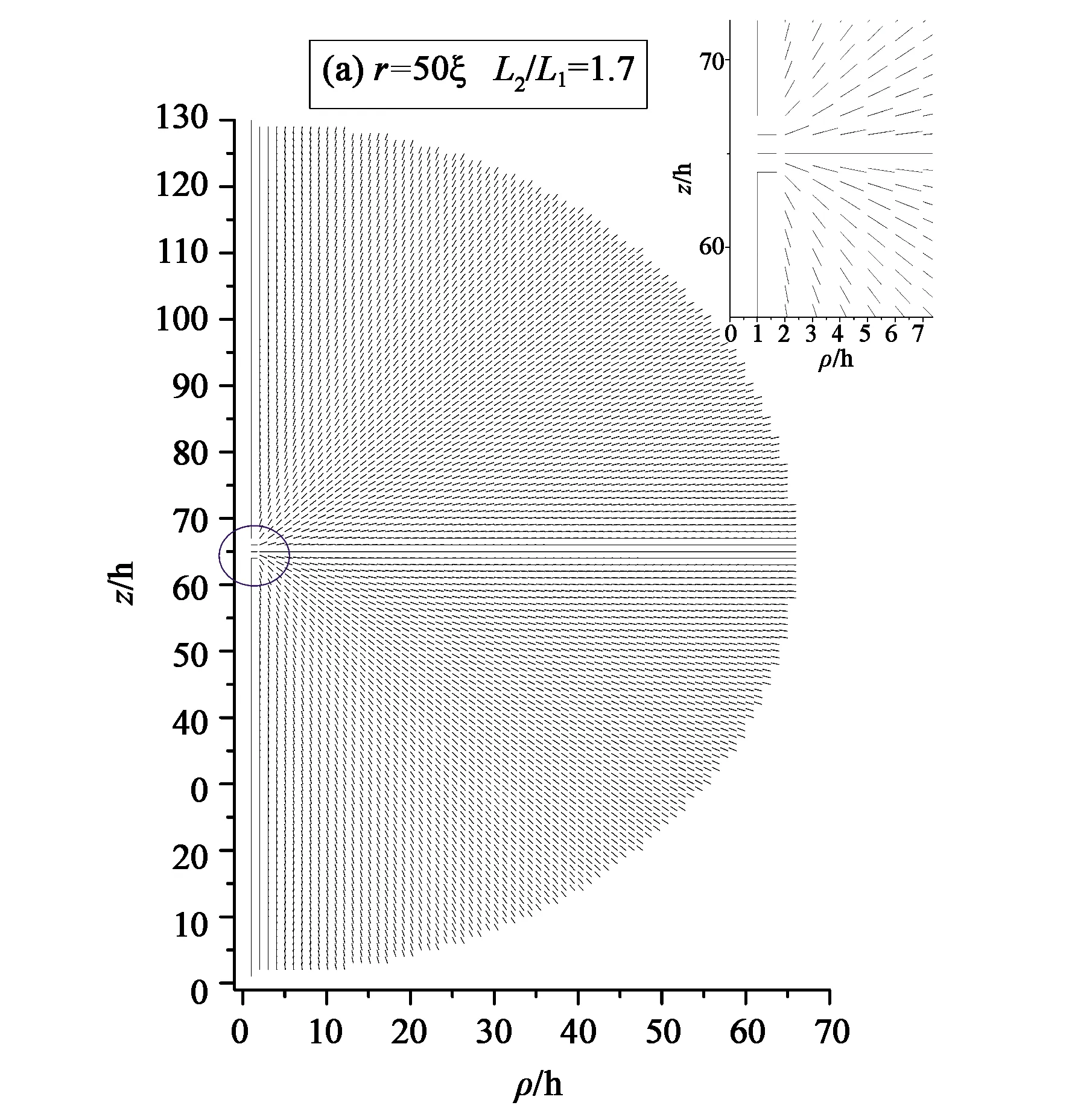
(a) 分裂核结构指向矢图(a)Profiles of the director of the split-core configuration

(b)中心轴的本征值，其中λ2=λ3。(b)Eigenvalues at the center axis, λ2=λ3.图3 半径为50ξ时分裂核结构图Fig.3 Profiles of the director of the split-core configuration when the radius is equal to 50ξ

当半径r=60ξ、L2/L1=2.2时，出现分裂核和环结构。对比能量发现环结构为稳态；而当半径r=70ξ，L2/L1=2.9时，出现分裂核和环结构，且分裂核结构始终为亚稳态。表2给出了分裂核和环结构的能量对比。

表2 强锚定不同半径下分裂核结构与环结构的能量对比Tab.2 Difference of energy between the split-core structure and the ring structure at different radius under strong anchoring

对于选取的小尺寸情况下的球形液滴，在强锚定边界条件下，当弹性常数L2/L1达到某个临界值时，径向结构不再稳定，而是转变为分裂核结构，但分裂核结构始终为亚稳态。

4.2 弱锚定下分裂核的稳定性——不考虑K24作用

上文研究了在强锚定边界条件下的径向结构、环结构与分裂核结构，下面从弱锚定边界条件的角度出发，固定边界锚定强度为w=10-4J/m2进行分析。

首先选取液晶微滴的半径为r=50ξ，在单一常数近似下，出现3种结构：径向结构、环结构和均匀结构。图4为均匀结构的指向矢图。如表3所示，径向结构仍然为能量最低态，根据Tomar等人的研究[9]，我们对此现象解释为此时的锚定强度较大，边界的指向矢仍然沿法线排列，更易形成径向结构，这里不再给出径向结构和环结构的指向矢图，只给出均匀结构的指向矢图。

图4 半径为50ξ时均匀结构指向矢图Fig.4 Profiles of the director of the uniform configuration when the radius is equal to 50ξ

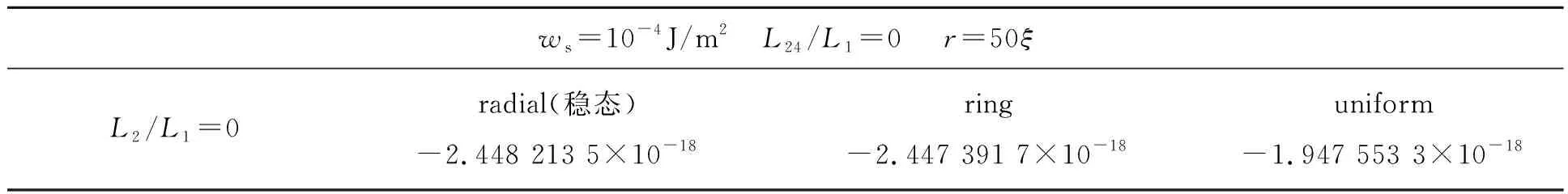
表3 弱锚定且弹性各向同性下3种结构的能量对比Tab.3 Difference of energy among three configurations under the isotropic elastic and weak anchoring mechanism

在弹性各向同性条件下，弱锚定边界条件机制使得小半径的球形液滴出现均匀结构，对于弹性各向异性，我们也做出了相应的模拟计算。

对于相同半径r=50ξ，当L2/L1增加时，会发现一些有趣的现象。如表4所示，当L2/L1的值等于0.5时，我们发现4种结构同时存在：径向结构、环结构、均匀结构和-1分裂核结构[8]。通过对比能量，发现均匀结构的能量最低，为稳态，其他3种结构均为亚稳态。当L2/L1的值等于0.7时，发现缺陷环的半径逐渐变大，径向结构不再稳定，而是转变为分裂核结构。当L2/L1=0.9时，环结构不再稳定存在而是转变为均匀结构。当L2/L1>2时，分裂核结构不再稳定存在，所以在0.7≤L2/L1≤2范围内，分裂核结构可以稳定存在，但总是为亚稳态，均匀结构能量最低，为稳态。

表4 弱锚定且弹性各向异性下不同结构的能量对比,其中L24/L1=0Tab.4 Difference of energy among different configurations under the elastic anisotropy and weak anchoring mechanism, L24/L1=0

固定锚定强度为w=10-4J/m2，选取弹性常数L2/L1=1.5、L24/L1=0，改变半径，发现分裂核结构在r=40ξ～100ξ范围内存在分裂核结构且为亚稳态，均匀结构为稳态。

4.3 弱锚定下分裂核的稳定性——考虑K24作用

首先选取半径r=50ξ进行研究，在单一常数近似下且不考虑k24作用即k24=0时，发现径向结构为稳态。根据前文研究，发现k24项可以作为表面项起作用[20]。如表5所示，当L24/L1达到Ericksen不等式最大值即L24/L1=2时，径向结构仍然为稳态。

在弹性各向异性下，我们对半径r=50ξ的液晶微滴做出了一系列模拟计算。对于分裂核结构，当 0.7≤L2/L1≤2时(此时L24/L1的取值限制在Ericksen不等式理论最大值范围内，即L24/L1≤2)，发现当0.7≤L2/L1<0.9，无论L24/L1取何值，环结构能量总是低于分裂核结构能量，即分裂核结构始终为亚稳态；当0.9≤L2/L1≤2时，环结构将不再稳定，而是转变为均匀结构；当L24/L1达到某个临界值时，分裂核结构成为能量最低态，而均匀结构成为亚稳态，这是在之前的研究中都未曾发现的。另外，对于-1分裂核结构，无论是否考虑k24作用，其始终为能量最高的态，因此不再详细论述。

表5 弱锚定且弹性各向异性下3种结构的能量对比，其中L24/L1=2Tab.5 Difference of energy among three configurations under the elastic anisotropy and weak anchoring mechanism, L24/L1=2

图5给出在Frank弹性常数中k22/k11与k24/k11之间的关系。蓝色区域内是分裂核结构可以存在的范围，而红色区域内是分裂核结构成为稳态的范围。黑色线为Ericksen不等式最大值时k22/k11与k24/k11之间的关系。

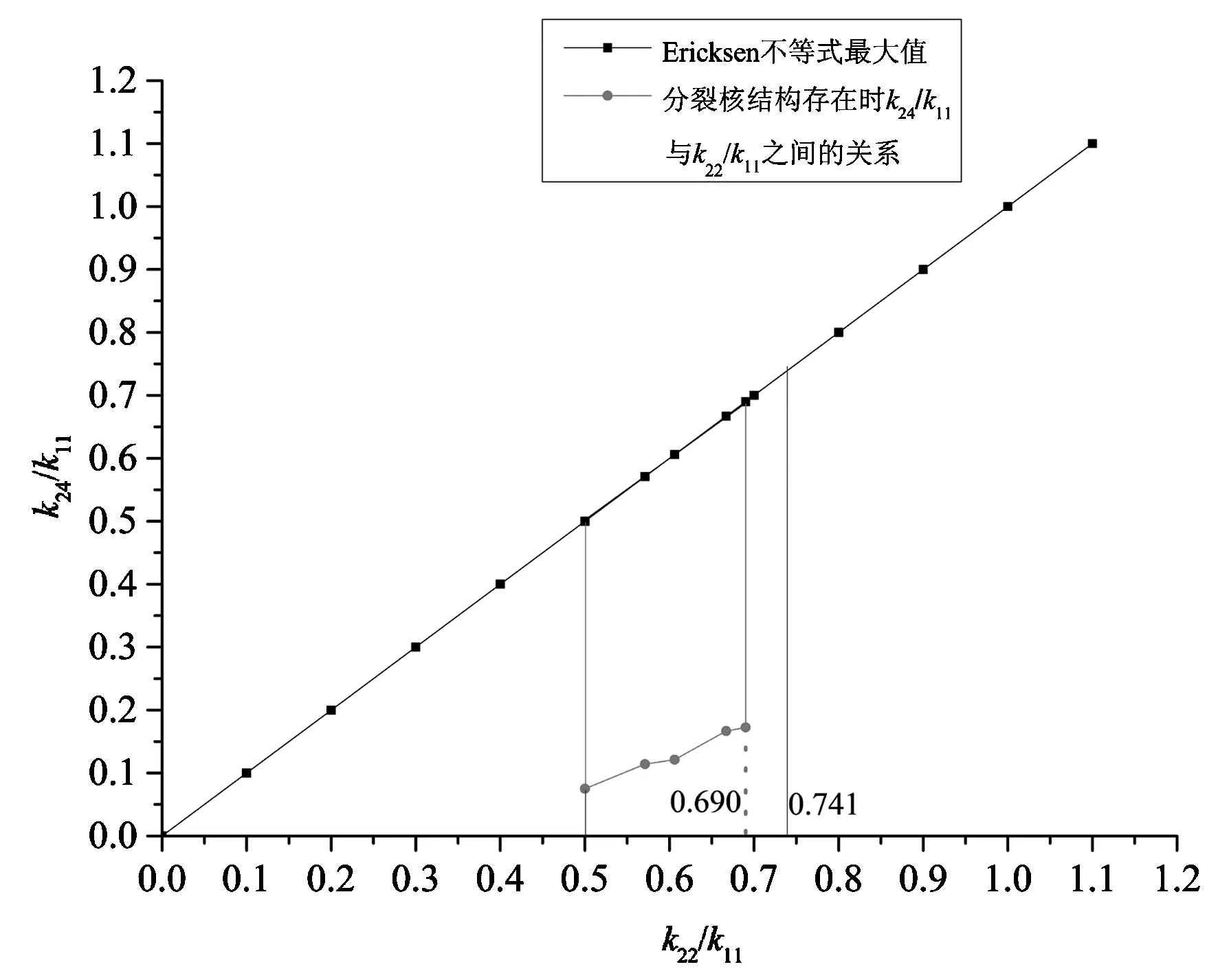
图5 分裂核结构存在时k22/k11与k24/k11的关系Fig.5 Relationship between k22/k11 and k24/k11 when the split-core configuration exists

其次，固定锚定强度w=10-4J/m2，选取弹性常数L2/L1=1.5、L24/L1=2(Ericksen不等式最大值)，改变半径，发现在r=40ξ～65ξ范围内分裂核结构成为能量最低态，均匀结构为亚稳态。此基础上又模拟计算了在w=10-4J/m2，r=40ξ～65ξ条件下，改变L24/L1，得到了分裂核结构和均匀结构的半径与能量相图，如图6所示。通过相图可以发现对于L24/L1=0，当r=40ξ～65ξ时，分裂核结构为亚稳态，均匀结构为稳态。对于L24/L1=0.5，当40ξ≤r≤46ξ时，均匀结构为能量最低态；当46ξ≤r≤65ξ时，分裂核结构为稳态。而对于L24/L1=1、L24/L1=2这两种情况，当r=40ξ～65ξ时，分裂核结构为稳态，均匀结构为亚稳态。

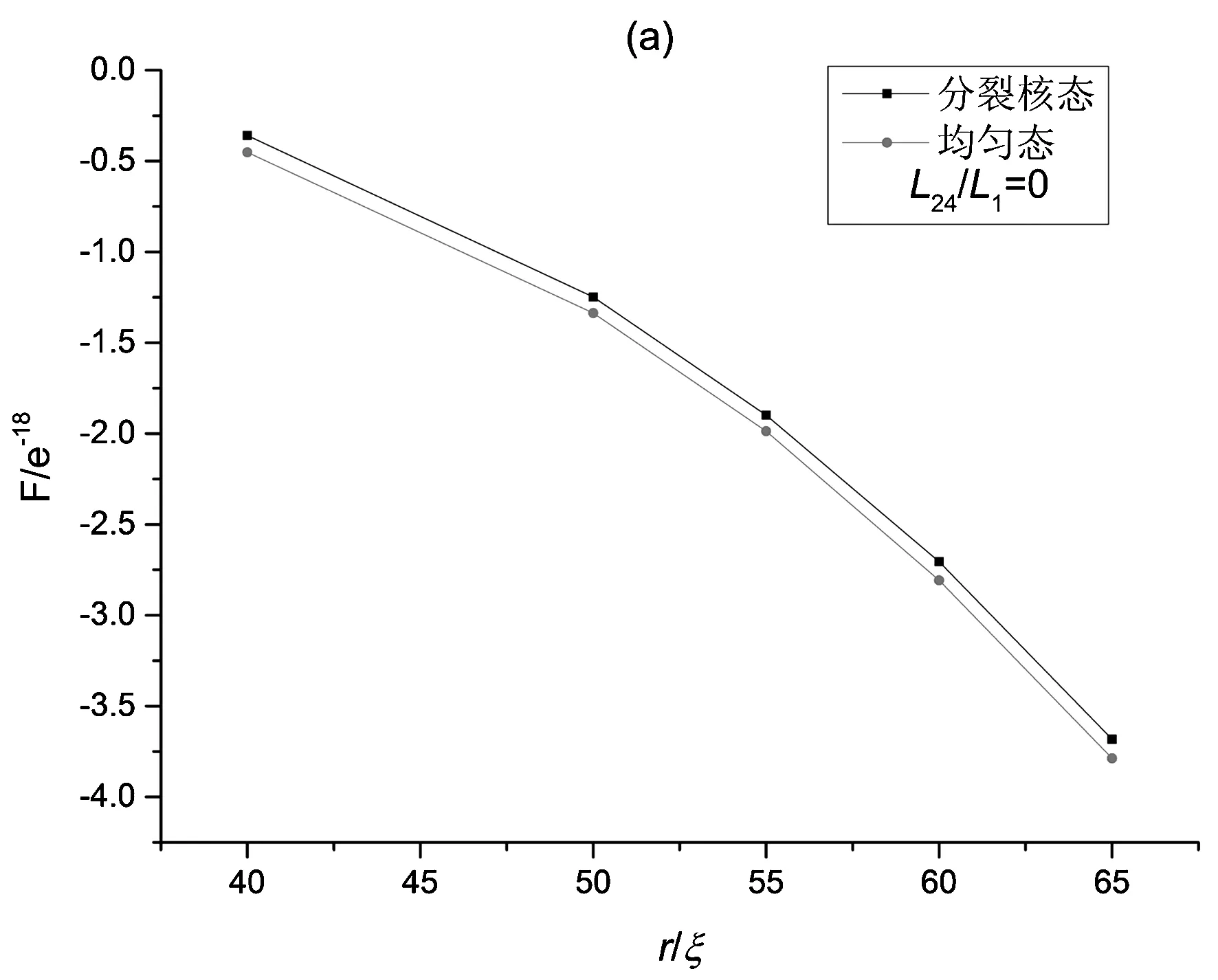
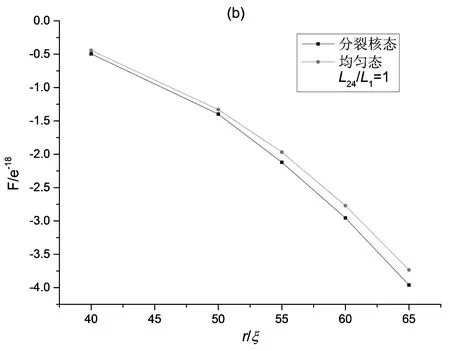
图6 分裂核结构与均匀结构的能量对比。(a) L24/L1=0；(b) L24/L1=1；(c) L24/L1=2。Fig.6 Difference of energy between the split-core structure and the ring structure； (a) L24/L1=0；(b) L24/L1=1；(c) L24/L1=2.

5 结 论

基于Landau-de Gennes理论，本文分别在强锚定和弱锚定边界条件下研究了径向、环、分裂核以及均匀结构的稳定性。首先在强锚定、温度一定且单一常数近似下，对于半径r=50ξ(132 nm)，同时存在径向和环结构，径向结构为稳态；对于半径r=150ξ(396 nm)，环结构为稳态，径向结构为亚稳态；并发现在r≥100ξ时，环结构为稳态，且当半径足够小时，只存在径向结构。其次在强锚定下，弹性各向异性使得径向结构内部结构发生了改变。选取r=50ξ、r=60ξ、r=70ξ的小尺寸液晶微滴进行研究，发现当L2/L1的值分别为1.7、2.2、2.9时，径向结构转变为分裂核结构，但分裂核结构总是为亚稳态，环结构为稳态。

对于弱锚定边界条件下，固定边界锚定强度为w=10-4J/m2，首先选取半径为r=50ξ进行研究，在不考虑k24作用即本文中Landau-de Gennes理论弹性常数取值为L24/L1=0时，单一常数近似下出现径向、环和均匀结构，此时径向结构仍为稳态；在弹性各向异性下，当L2/L1=0.5时，径向结构、环结构、均匀结构和-1分裂核结构同时存在，此时均匀结构为稳态；随着L2/L1的取值增大，环结构中的缺陷逐渐向赤道表面靠近，当L2/L1=0.7时，径向结构转变为分裂核结构，此时Frank理论的弹性常数k11/k22的比值大于1，即展曲弹性常数k11的值变大，使得系统中更难形成展曲形变，由于径向结构具有良好的展曲形变，所以此时径向结构不再稳定存在。当L2/L1=0.9时，环结构不在稳定存在，而是转变为均匀结构。当L2/L1=2时，继续增加取值分裂核结构不再稳定，因此分裂核结构稳定存在的范围为0.7≤L2/L1≤2，此条件下对比能量发现分裂核结构始终为亚稳态，均匀结构为稳态，对于出现的-1分裂核结构，由于其能量始终最高并伴随其他态共存，这里不再详细介绍。对于固定L2/L1=1.5，改变不同半径，发现当r=40ξ～100ξ时分裂核结构可以存在且为亚稳态。

本文首次探究并给出了在弱锚定边界条件且考虑k24项作用(即L24/L1≠0)时，分裂核结构可以成为能量最低态。首先选取半径r=50ξ进行研究，对于单一常数近似，L24/L1的取值达到Ericksen不等式理论最大值时(L24/L1=2)，径向结构为稳态；对于弹性各向异性，当0.7≤L2/L1<0.9时，无论L24/L1取何值，分裂核结构始终为亚稳态，均匀结构成为稳态；对于0.9≤L2/L1≤2，当L24/L1达到某个临界值时，分裂核结构成为能量最低态，均匀结构成为亚稳态。固定L2/L1=1.5、L24/L1=2，改变不同半径，发现当r=40ξ～65ξ时，分裂核结构成为能量最低态，均匀结构为亚稳态，并通过改变L24/L1，得到了分裂核结构成为能量最低态的范围。