基于GAM方法的组合预测模型及其应用
2021-04-10卢整智高小燕施晓燕
卢整智,高小燕,施晓燕
(1.兰州城市学院 数学学院,甘肃 兰州 730070;2.甘肃农业大学 理学院,甘肃 兰州 730070;3.西南财经大学 统计学院,四川 成都 611130)
0 引言
近年来,我国许多城市空气质量恶化,不断遭到灰霾天气的侵袭,尤其是2013年春冬两季我国出现大范围、持续性霾污染,致使PM2.5成为热议.PM2.5指环境空气中空气动力学当量直径小于等于 2.5 微米的颗粒物,它能较长时间悬浮于空气中,其在空气中含量浓度越高,就代表空气污染越严重,与较粗的大气颗粒物相比,PM2.5粒径小,面积大,活性强,易附带有毒、有害物质,且在大气中的停留时间长、输送距离远,对人体健康和大气环境质量产生了非常严重的影响.因此,对PM2.5浓度做出科学的预测已成为城市环境质量监控的重要指标.纵观国内外对PM2.5浓度的预测研究,大多采用的是单项预测模型,比如张玉丽等[1]和刘文军等[2]运用了多元回归模型;许晟昊[3]和谢心庆等[4]采用了时间序列模型;韩婧等[5]采用了灰色预测模型;刘宇轩等[6]和李燚航等[7]采用了机器学习等预测方法,这些方法各有偏重,各有优势,但预测精度普遍不高.陈华友等[8]和程春英等[9]的研究表明,预测精度低是因为PM2.5不是一种单一成分的空气污染物,而是由许多不同的化学成分一起组成的复杂可变的大气污染物,单一模型很难全面、准确地反映PM2.5浓度的变化规律,所以预测精度较差.针对这一问题,本文尝试采用灵活稳健的非参方法GAM模型从非线性的角度将单个预测模型组合之后预测兰州市空气中PM2.5的浓度,以期提高模型预测精度.首先分别使用自回归移动平均模型(ARMA)、条件异方差模型(ARCH)、非参数自回归模型(NAR)对兰州市PM2.5浓度进行预测,再利用基于等权组合法、误差平方和倒数法、最优权数法的组合预测模型预测兰州市PM2.5浓度,最后利用基于GAM模型的组合预测模型对兰州市PM2.5浓度做出预测,并比较了所有预测模型的有效性.
1 研究思路与研究方法
建立组合预测模型包括以下步骤:①单项预测模型的选择.能否正确选择单项预测模型直接影响预测结果的准确性,因此,在实际应用中应将研究对象的特点与单项预测模型的原理及条件结合起来,选择合适的单项预测模型.②单项预测模型的组合方式.按照何种方式将不同的单项预测结果有效组合起来是提高组合预测模型的关键.③组合预测模型评价.构建好组合预测模型之后,还需选取评价模型优劣的指标反映组合预测模型的有效性.
1.1 单项预测模型的选择
1.1.1 线性时间序列模型
最普通的线性时间序列模型为自回归移动平均模型(ARMA(p,q)),该模型常被用来描述响应变量与其延迟变量间的线性关系,结构为
(1)
其中:φ(B)=1-φ1B-…-φpBp为平稳可逆ARMA(p,q)模型的自回归系数多项式;θ(B)=1-ϑ1B-…-ϑqBq为平稳可逆ARMA(p,q)模型的移动平均系数多项式.
假定某个观察值序列若通过预处理可以判定为平稳非白噪声序列,就可以利用ARMA模型拟合它.然而,在实际数据分析中,序列可能会呈现出时间趋势或循环特征,并非平稳序列,这就需要先对数据作差分消除趋势性或季节性使之变平稳后再用ARMA模型进行拟合.
从Yule(1972)关于太阳黑子数ARMA建模的开拓性工作至今,线性时间序列模型研究取得了极大的进展,许立平等[10]认为由于线性时间序列模型简单、灵活,所以在应用时间序列分析中发挥着积极的作用.
1.1.2 非线性时间序列模型
19世纪50年代,P A P Moran在对加拿大山猫数据建模的文章中提到了数据的“怪异”特征,即后来被解释为在种群波动的不同阶段有“控制效应”,这种特征超出了线性时间序列模型研究的范围,如若再用线性时间序列分析的方法拟合这种序列,会丢失大量的信息,拟合效果不佳,因此,张延利等[11]开始了对非线性时间序列模型的研究.
非线性时间序列模型早期的发展主要是参数非线性模型,有自回归条件异方差模型(ARCH)、门限自回归模型(TAR)、平滑转移模型(STR)、指数自回归模型(EXPAR)及双线性模型(BL)等.近年来,随着计算机的发展,非线性、非参数模型作为一种新方法,以更高的估计精度在时间序列分析中越来越广泛地被应用,主要有非参数自回归模型(NAR)、非参数VAR模型族、非参数面板模型等,非线性、非参数时间序列模型的优点在于让数据说话,克服了特定参数模型的主观性.
根据兰州市PM2.5浓度的数据特征,本文选取条件异方差模型(ARCH)和非参数自回归模型(NAR)对序列进行预测,以下是对这两个模型的介绍.
(1)ARCH模型
假设时间序列{Yt}服从如下回归模型:
Yt=Xt′ξ+εt,
(2)
其中:Xt′是解释变量向量,它可以包含解释变量的滞后项;ξ是回归参数向量;{εt}是扰动序列,如果扰动序列{εt}满足:
εt|Ωt-1~N(0,σ2),ht=h(εt-1,…,εt-q) ,
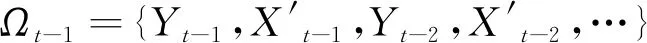
(2)NAR模型
假设{Yt}为一时间序列,Xt∈Rp是由Yt∈R的滞后项组成,即Xt=(Yt-1,Yt-2,…,Yt-p)′,则NAR模型可以描述为
Yt=m(Xt)+εt,
(3)
扰动序列{εt}独立同分布且满足:
E(εtεs)=0,s≠t,E(Xsεt)=0,∀s 在NAR模型中,采用Chen和Tang提出的Cross-Validation方法来确定滞后阶数p,其原理是:令Xt(p)=(Yt-1,Yt-2,…,Yt-p)′,定义 目前,国内外很多领域的预测大多采用单项模型,但是单项模型都有各自的特点和应用的局限性,且使用数据的信息有限,因此,近年来,一些学者创新性地建立了组合预测模型.比如莫东序[12]和王学梅等[13]分别运用组合预测模型对中国GDP和PM2.5进行了预测,结果表明组合预测模型的预测精度高于单一预测模型.理论和实践研究都表明,在诸种单个预测模型各异且数据来源不同的情况下,组合预测模型比任何一个独立预测模型的预测结果都好,且组合预测模型能够减少预测的系统误差,显著改进预测效果. 组合预测模型的普遍形式是采用不同的单项预测模型对同一问题进行预测,再将单项预测模型进行加权平均得到组合模型,如果加权系数赋值合理,组合预测模型的预测精度会相应提高.目前,学者们常用的赋权方法有等权平均法、误差平方和倒数法和最优权数法,下面分别介绍这三种方法. 1.2.1 等权平均法 (4) 1.2.2 误差平方和倒数法 (5) 1.2.3 最优权数法 最优权数法的基本原理是:首先依据某种最优准则构造目标函数Q,再在约束条件下极小化Q,求得组合模型的权系数.其中目标函数依据误差而定,如绝对误差、误差平方和等.目标函数的极小化准则有最小二乘准则、极小极大化准则等.最优权数组合预测模型的定义为: 的解,其中: 于是,该组合预测模型为 (6) 论文1.2节介绍的三种组合预测模型中,基于等权平均法和误差平方和倒数法的组合预测模型虽然在给单项预测模型赋权时原理简单、便于计算,但是事先已经设定了组合模型的形式,预测效果不是很理想.最优权数法组合预测模型的建立严格依赖于最优准则,另外对于最优权重问题到现在也没有定论,鉴于此,本文尝试采用基于广义可加模型(GAM)将单个预测模型进行组合,以期克服以上组合预测模型的缺点. GAM模型一般用来探测非线性回归,形式为 (7) 其中:α为截距项;fi(·)是平滑函数,是针对于每个解释变量的任意单变量函数,是非指定类别的非参数函数,其估计方法可以是局部多项式回归函数、光滑样条函数,平滑参数的选择可以是交叉验证法和广义交叉验证法,Y的分布可以是正态分布、卡方分布和二项分布等.广义可加模型是由多元线性回归模型变换而来,无需再去设定变量之间是线性关系,模型应用更为广泛,可以探寻到变量间的真实的关系.其关键就在于对于线性回归模型的因变量做了函数处理,这就需要用非参数回归方法估计函数的形式. 非参数回归方法是近年统计学发展的重要方向,在实际应用中因其具有不需要先验知识、不需要预先设定回归函数的具体形式、适应能力强、稳健性高及回归模型完全由数据驱动等优点被广泛关注.非参数回归模型的基本形式: Y=m(X1,X2,…,Xp)+ε. (8) 对式中的m(X)只作连续性或光滑性的要求,ε~NID(0,σ2).目前已有多种估计m(X)的方法,最基本的有核估计、局部多项式回归和光滑样条回归等.但是当模型中的自变量个数较多时,以上方法的估计方差会加大,此外,基于核与光滑样条估计的非参数回归中自变量与因变量之间关系解释起来非常困难.于是1985年Stone 提出加性模型AM (Additive Models),模型中每一个加性项使用单个光滑函数来估计,每一加性项中可以解释因变量如何随自变量变化而变化,很好地解决了上述问题. 不同模型对同一现象的预测效果不尽相同,如何从这些模型中选出一个预测精度较高的模型是预测建模过程中的一个重要问题. 目前各类预测方法所使用的误差评价指标大多直接采用统计学指标评价模型预测结果,主要有误差均值(ME)、绝对值平均误差(MAE)、均方根误差(RMSE)、平均相对误差(MRE)、误差平方和(SSE)和平均绝对百分比误差(MAPE)等,在PM2.5预测中,常用的指标有SSE和MAPE,以下是这些指标的定义. (9) MAPE指标定义为 (10) 其中,ME指标没有考虑到预测时出现正负误差相抵导致ME是一个较小的值,可能对结果造成误判; SSE和MAPE不存在正负抵消,都是基于先逐点求和再平均的思想,易于计算,可以对预测模型的优劣做评价. 以中国空气质量在线监测平台(https://www.aqistudy.cn/) 的数据为来源,选取兰州市PM2.5浓度自2019年5月1日至2020年12月21日每天收集的数据600条,缺失数据8个,采用K近邻方法进行插补.本文所有的统计分析均使用R 3.3.1软件. 2.2.1ARMA模型预测结果 在建立ARMA模型之前,需要检验序列的平稳性和纯随机性.采用ADF检验兰州市PM2.5序列的平稳性,得到的P值为0.0278,故拒绝存在单位根的原假设.用LM-Q统计量检验序列的纯随机性,得到的P值为0.0435,故拒绝序列为纯随机序列的原假设.由以上检验结果可知:兰州市PM2.5序列为平稳非纯随机序列,故可用ARMA模型进行拟合.下面做出序列的自相关系数(ACF)图(如图1所示)和偏自相关系数(PACF)图(如图2所示),来确定模型的滞后阶数. 图1 兰州市PM2.5的自相关系数图 图2 兰州市PM2.5的偏自相关系数图 由图1的自相关系数图可以看出,序列的ACF 6阶截尾;由图2的偏自相关系数图可以看出,序列的PACF 2阶截尾,因此很难用传统的B-J方法确定模型的阶数,只能通过反复对模型进行估计比较不同模型的参数及总体显著性确定模型的阶数.首先用MA(6)、AR(2)和ARMA(1,6)拟合原序列,剔除不显著变量后依据AIC准则选出最优模型为疏系数模型ARMA(1,(1,6)),拟合结果如表1所列. 表1 兰州市PM2.5浓度的ARMA(1,(1,6))模型预测结果 2.2.2 ARCH模型预测结果 先做出兰州市PM2.5的时序图(如图3所示),直观上判断序列是否存在波动性和及集聚性.从图3可以看出,兰州市PM2.5呈现出一段时间内波动性较高,另一段时间内又出现较小波动的现象,表明兰州市PM2.5浓度具有集群效应,该序列存在异方差性.因此,需要先用ARMA模型提取序列的线性相关性,再对残差序列用ARCH-LM方法进行异方差检验,看是否适合建立ARCH模型拟合存在异方差性的残差序列. 图3 兰州市PM2.5的时序图 由2.2.1的分析可知,可先对兰州市PM2.5浓度用ARMA(1,(1,6))进行预测提取线性成分,再对残差序列进行ARCH效应检验,结果如表2所列. 表2 残差序列的异方差ARCH-LM检验 由表2结果可知,F统计量显著,表明残差序列存在ARCH效应,因此,可以对残差序列采用ARCH(1)模型进行拟合,消除异方差,模型估计结果如下: 2.2.3NAR模型预测结果 对兰州市PM2.5建立非参数自回归模型: PMt=m(PMt-1,PMt-2,…,PMt-p)+εt, (11) 其中:{εt}独立同分布,且满足: E(εtεs)=0,s≠t,E(Xsεt)=0,∀s 2.2.4 基于GAM模型的组合预测 (12) 其中,fi(·)(i=1,2,3)为自然立方样条,通过最小化惩罚残差平方和得到. 其中,λj为调节参数,其可以平衡数据的拟合优度和待估参数的光滑度.本文通过R 3.3.1中的MGCV程序包拟合GAM模型得到,通过最小化GCV(Generalized Cross Validation)来适当选择调节参数,GCV的定义为: 为了验证本文提出的基于GAM的组合预测模型的有效性,参考已有研究,选用1.4节式(9)表示的误差平方和(SSE)和式(10)表示的平均绝对百分比误差(MAPE)两个指标评价模型的预测效果.预测模型的SSE和MAPE的值越小,表明预测值偏离真实值的程度越小,模型的预测效果越好.分别计算ARMA模型、ARCH模型、NAR模型、基于等权平均的组合预测模型、基于误差平方和倒数法的组合预测模型、基于最优权数法的组合预测模型、基于GAM的组合预测模型预测的兰州市PM2.5浓度的SSE和MAPE,结果如表3所列. 表3 各预测模型的SSE和MAPE 从表3的结果可以看出,3个单项预测模型的SSE和MAPE均大于4种组合预测,验证了组合预测模型的预测效果优于单项预测模型.本文提出的基于GAM方法的组合模型的SSE和MAPE均小于其他三种组合预测模型,其预测效果最好. 由于单项模型各自的缺陷及利用的信息有限,用单项模型进行预测时一般误差较大,而通过一定的方式将单项预测模型进行组合可以提高预测精度.但是现有的组合预测模型大都是利用不同的准则确定了单项模型的权重,而在现实中,单项模型预测值与原序列值的关系通常是很复杂的,而GAM模型恰好可以刻画被解释变量与解释变量之间的复杂关系,因此,本文提出基于GAM方法的组合预测模型,且通过实证分析了该模型的有效性. 实证结果表明:基于GAM方法将ARMA、ARCH和NAR组合起来的预测模型不光优于这三个单项预测模型,还优于利用等权平均法、误差平方和倒数法和最优权数法等组合的预测模型,具有很好的应用前景.
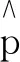
1.2 单项预测模型的组合方式
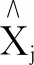

1.3 基于GAM方法的组合预测模型
1.4 模型评价

2 基于GAM方法的组合预测模型的应用
2.1 数据来源及说明
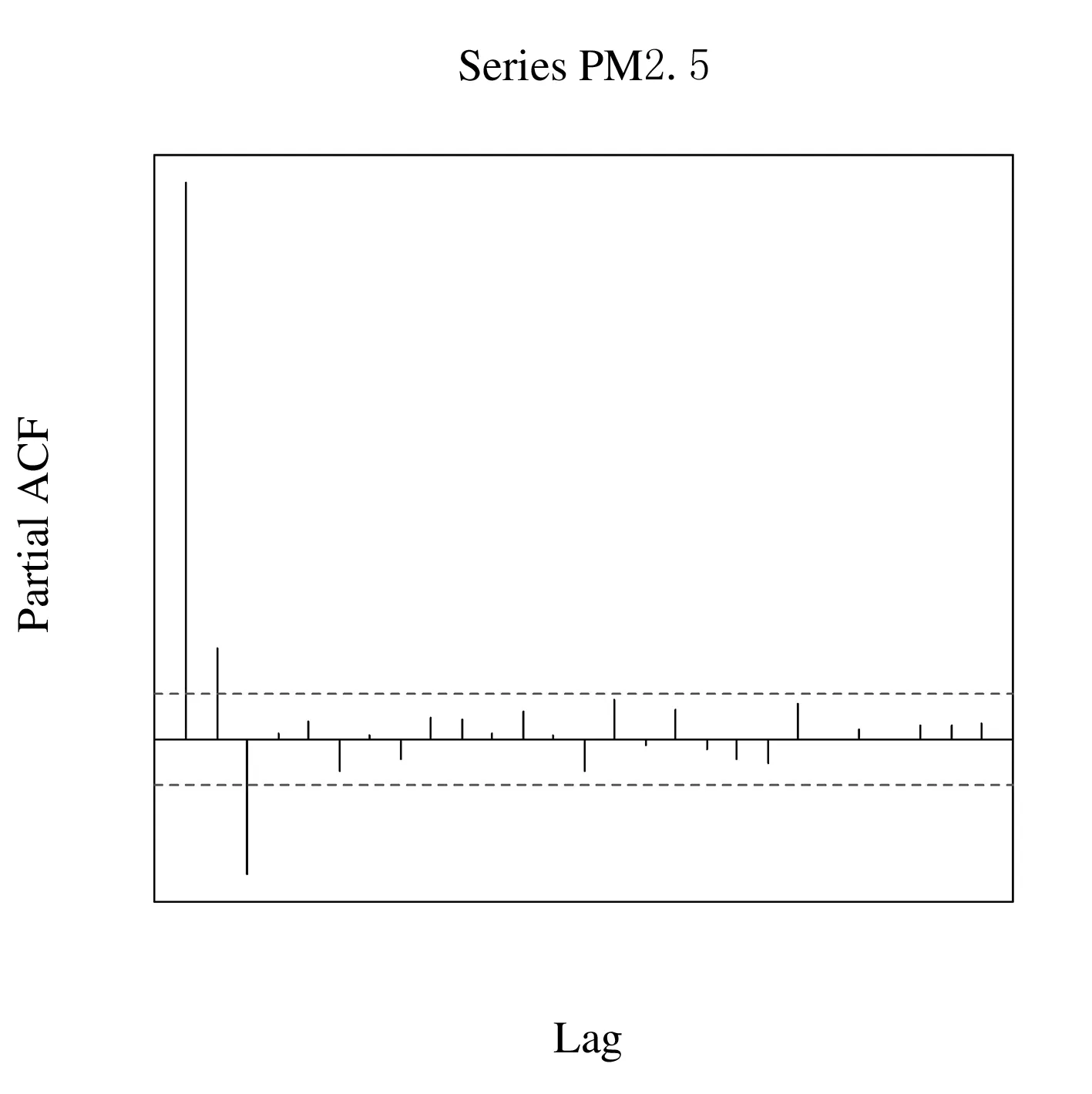
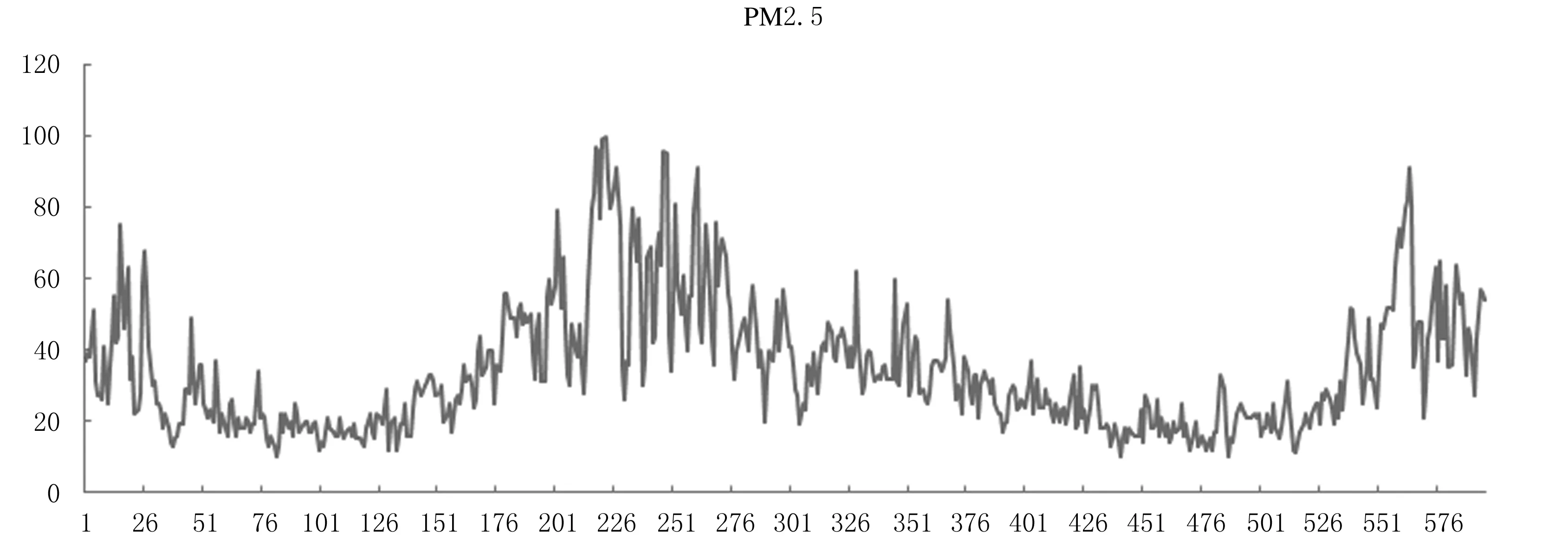
2.2 PM2.5浓度预测






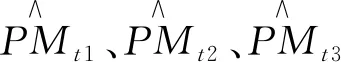
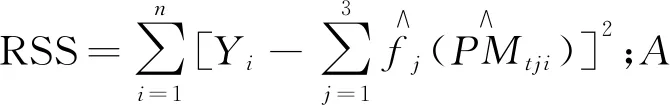
2.3 不同模型的预测效果评价

3 结束语
