多源数据对林分动态预测的影响及不确定性分析*

田相林 廖梓延 孙帅超 薛海连 王 彬 曹田健

1.西北农林科技大学林学院 生态仿真优化实验室 杨凌 712100； 2.赫尔辛基大学林学系 赫尔辛基 FI-00014； 3.中国科学院成都生物研究所 成都 610041； 4.中国科学院大学 北京 100039； 5.福建农林大学 福州 350002； 6.西北农林科技大学理学院 杨凌 712100； 7.青海大学农林科学院 西宁 810016)

在森林立地、密度效应、林分生长以及经营措施等方面的理论研究中，森林建模往往要求林分观测数据是一种控制试验的产物，并假定试验是被设计在严格可控的环境中以检验特定变量对林分生长动态的影响。然而，受限于控制森林生态系统环境的能力、调查所能承担的时间和空间范围以及观测到特定变量的能力等，森林动态预测研究通常依赖于有限数量并伴随复杂误差结构的数据，使得经典统计模型的假设情境往往难以被满足(Clark， 2007)。在森林生态系统研究中，林分生长收获分析需要综合多种数据类型，如临时样地、固定样地、解析木和生长锥木芯等，这些信息由于采用不同抽样设计或观测方法等原因常常具有极其复杂的误差结构特征，且其复杂程度会随不同时期或类型的新数据加入而不断累积。同时，在林分动态预测与生长收获模型应用研究中，来自非控制条件下部分观测过程的信息往往需要作为统计推断的基础(Dietze， 2017)，诸多不可控的环境或机制因素都会导致森林调查数据与林分动态预测之间形成复杂的信息交互体系，最终使得模拟与预测的可靠性无法被量化评价。

随着生态系统探讨问题的复杂性不断升高，现代模拟和计算技术被广泛应用于相关领域研究中，其中，贝叶斯框架的潜在假设使得贝叶斯方法不再受模型数据量和控制条件等因素制约，且具备综合多源数据信息的能力(Clarketal.， 2007)，其应用在20世纪90年代后飞速发展(Gelfandetal.， 1990； Berger， 2000)，并逐渐被林业研究者所关注(Greenetal.， 1996； Bullocketal.， 2007； Clarketal.， 2007； Metcalfetal.， 2009)。贝叶斯估计值同时依赖于先验和后验分布，复杂问题的后验信息往往由迭代数据随机取样来确定，即产生参数的完整后验分布，这意味着许多统计值可从生成的样本中获得。尽管经典的最大似然方法和贝叶斯方法会产生相似的参数估计(Lietal.， 2011)，但贝叶斯方法不需要像最大似然方法那样的附加条件和特定的分布假设，贝叶斯框架下林分模型的构建，可极大限度减小统计学假设对数据的限制，并能对模型本身和林分生长的不确定性进行合理量化分析(Hartigetal.， 2012)。基于Tylor展开式或Monte Carlo抽样方法推断或预测的不确定性可以解析为不同的来源，包括数据的不确定性、模型结构的不确定性和模型参数的不确定性，进而对不确定的传递过程进行量化(Lebaueretal.， 2013； Dietze， 2017)，其中多维相关性基础上的参数不确定性是生态系统模型开发与应用中难以回避的内容(Van Oijen, 2017)。

在森林动态预测研究中，贝叶斯方法也逐步得以应用，如地上生物量模型(Zapata-Cuartasetal.， 2012； Zhangetal.， 2013)、直径分布模型(Bullocketal.， 2007)和直径生长模型(Clarketal.， 2007)等。贝叶斯方法的核心优势在于其对数据与模型关系的描述，如估计多层次/体系模型(Gelmanetal.， 2007； Dietzeetal.， 2008)、利用有限数据信息校正复杂模型(Van Oijenetal.， 2005)、从不同模型中合并预测值(Radtkeetal.， 2006)以及克服数据稀疏问题(Metcalfetal.， 2009)等，而目前森林建模研究中，贝叶斯框架下数据与模型间信息融合与复杂误差结构的讨论往往集中于过程机制模型而非经验模型(Hartigetal.， 2012； Dietze, 2017； Van Oijen， 2017)。森林生长收获经验模型的主流仍然是基于系统性设计的长期观测(Pretzsch， 2010)，并对数据的误差体系有着详尽考量(Kangasetal.， 2006)； 然而这种大量建模数据的需求，在国内多数林区难以满足。由于缺少系统性的长期观测，且数据误差随不同抽样策略或数据源而剧烈波动，使得经典回归分析理论中的许多假设并不成立，因此将误差结构纳入模型体系尤为重要(唐守正等， 1995； 1998； 符利勇等， 2014)。

从森林生长收获模型的尺度上来说，全林模型只需要相对较少的信息来模拟林分生长。相比径阶和单木模型，全林模型所模拟的基本单元是林分和立地参数，包括年龄、林分断面积、立地指数和蓄积量等，虽然无法像径阶或单木模型一样分析林分结构的动态变化，但全林模型可以保证较为准确的未来林分蓄积生长状况信息，这在森林经营实践中非常重要(Weiskitteletal.， 2011)。可变密度全林模型将林分密度作为继林分年龄、立地质量的第3个变量，可以描述特定树种和立地条件下任意林分的生长，在密度控制和森林经营规划中有着广泛应用(张少昂， 1986； 李希菲等， 1988； 唐守正， 1991； 1993； 1999； 洪玲霞， 1993； 洪玲霞等， 2012； Weiskitteletal.， 2011)。

本研究以数据信息要求较低、应用广泛的可变密度全林模型为例，采用贝叶斯数据-模型框架，构建森林资源连续调查中数据信息融合与模型学习的关系，探究随着新一期数据不断加入，模型参数概率分布和模型预测结果的变化规律； 在考虑误差分布和异方差等特征的基础上，比较角规临时样地、矩形固定样地、树干解析3种数据类型对模型构建和林分动态模拟的影响，以提高模型预测的准确性和可靠性； 同时，基于不确定性的量化评估，为森林调查中的数据收集策略提供建议。

1 数据与方法

1.1 数据

模型开发数据源自陕西省宁陕县火地塘林区(108°21′—108°39′E，33°18′—33°28′N)和旬阳坝林区(103°58′—109°48′E，32°29′—33°13′N)。数据采集海拔范围为1 200～1 800 m，坡度范围为15°～42°。土壤为森林棕壤，平均厚度50 cm。该区域属亚热带湿润山地气候，年均气温8～12 ℃，年均降雨量1 100 mm。这2个林区原始天然林于20世纪60—70年代进行过采伐，目前多为天然次生林或人工林。研究区样地位置分布见图1。

研究共使用215块角规绕测临时样地、22块20 m×20 m矩形固定样地和11株中等木解析木，所有样地均为油松(Pinustabulaeformis)纯林(油松断面积占比高于90%)或相对纯林(油松断面积占比65%～90%)。角规断面积系数为1 m2·hm-2。角规绕测临时样地调查数据包括1990年森林经理调查(李悦黎等， 1993)获得的58块油松相对纯林样地和2005年森林经理调查获得的68块油松相对纯林样地。为减少抽样设计带来的误差，采用完全相同的方法于2012年补充调查45块油松样地，最终获得3期角规样地调查数据(表1)。除了角规绕测临时样地以外的 22块矩形固定样地和11株油松中等木树干解析数据，被用于比较不同数据类型对模型表现的影响，全部数据对比见表2。

本研究多源数据包括森林生长收获建模中2种常见的数据状况： 一为相同抽样设计下不同时期的调查数据(表1)，数据误差结构不同多为设备、人员和质量控制差异造成； 二为不同抽样设计本身导致误差的系统性差异，即本研究中点抽样的临时样地、每木检尺的矩形固定样地、解析木(表2)在抽样和林分调查因子测算原理上存在系统性区别。

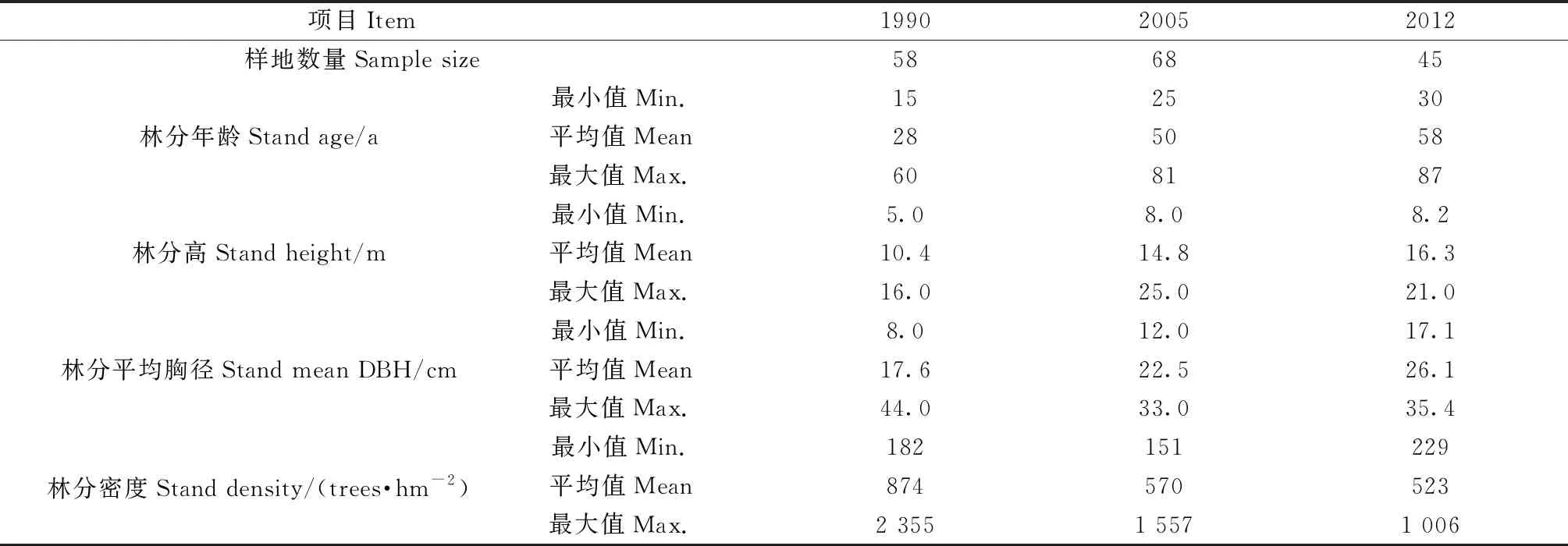
表1 用于模型循环更新测试的3期角规样地调查数据

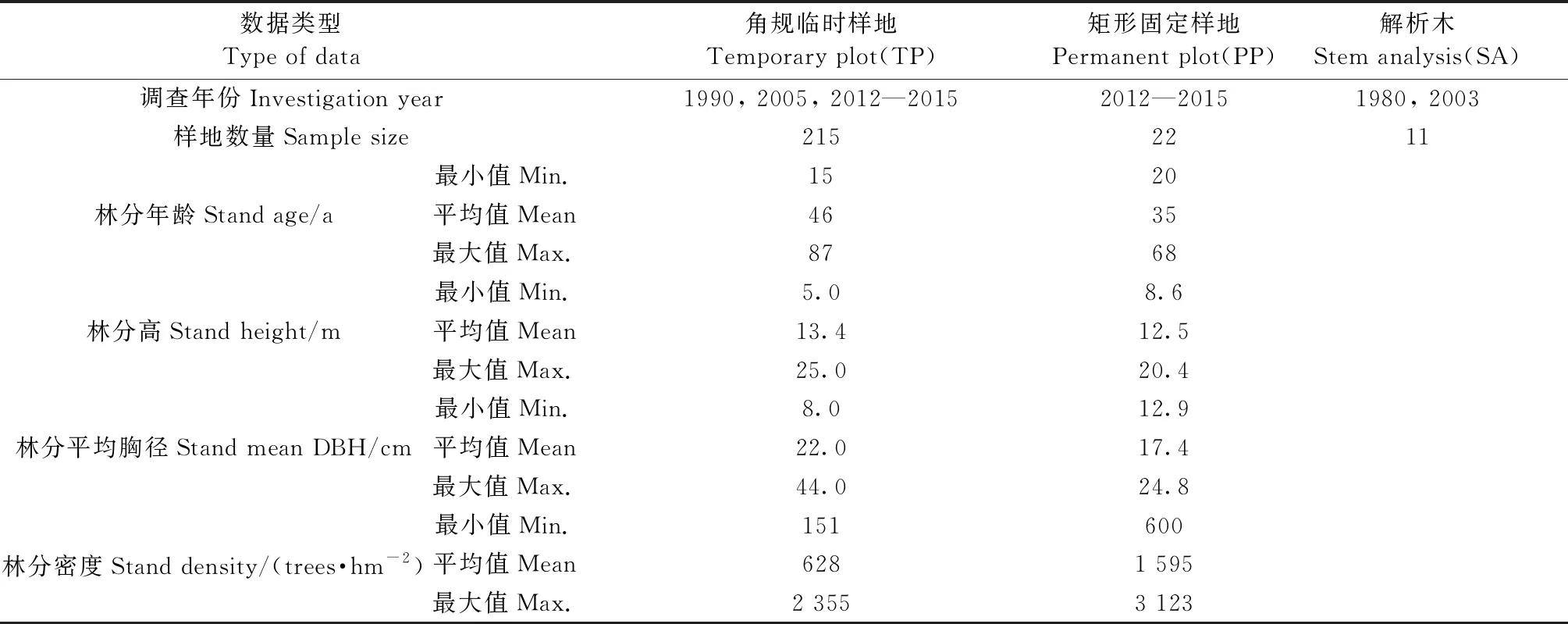
表2 模型构建中比较的3种数据类型

1.2 可变密度全林模型

可变密度全林模型仅需对基础林分调查信息进行参数化，可用于模拟给定林分的平均高H(m)、断面积G(m2·hm-2)、平均胸径D(cm)等。模型体系如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

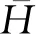
根据油松生长曲线和数据中的树高变动系数，设置A0=30 年(吴恒等， 2015)。通过调整SDI和SCI，可模拟不同林分密度和立地质量的林分生长过程。整个模型体系不依赖于固定样地的连续复测，林分密度变化由断面积与平均胸径的关系获得。

关于本林区不同数据集和指标对立地评价的具体影响以往研究已进行了详尽探讨(吴恒等， 2015； 郭小阳等， 2017)，本研究之所以采用给定年龄下的林分平均高期望值，即地位级指数用于林分立地质量评估，是因为1990和2005年的调查数据中许多样地缺少优势木记录，无法构建常规立地指数曲线。林分平均高导向曲线、林分总断面积模型和平均胸径模型均采用Schumacher模型(Schumacher， 1939)的基本结构。树高模型拟合同时测试临时样地、固定样地、解析木3种数据类型，胸径和断面积模型仅比较临时样地和固定样地2种数据类型。林分密度指数推算基于完满立木度林分密度(N)与平均胸径(D)的关系，即需要完满立木度林分数据，采用逐步剔除(李希菲等， 1988)对样地进行筛选： 1) 利用全部数据拟合Reineke(1933)方程lnN= α-βlnD； 2) 舍弃所有低于该方程回归线的低密度林分，并用剩余数据继续拟合该方程； 3) 舍弃低于新回归线的所有样地。剩余样地假定其为完满立木度并重新拟合该方程，最终获得式(1)中的参数β。分别完成地位级指数和林分密度指数模型拟合后，各样地SCI和SDI通过计算得到，进而依次完成林分断面积和胸径模型拟合。方程组联立求解参数依1.4节操作。

1.3 贝叶斯数据-模型框架

贝叶斯方法提供数据信息融合与模型学习框架，新的数据信息可不断加入模型中，该过程可以简单地表述为：

p(θ|D)∝p(D|θ)×p(θ)。

(8)

式中：p(θ|D)和p(θ)分别为模型参数θ的后验和先验分布；p(D|θ)为似然函数，即给定参数θ时数据D被观测到的概率。

对于过程机制模型，先验分布通常基于生理学观测数据或理论推测的范围(Van Oijenetal.， 2005)。对于参数数量较少且没有生理学含义的经验模型，在首次校正(参数拟合)时，采取无信息先验方式，参数联合后验分布取决于似然函数，而之后的数据融合与模型更新过程中，将前一次拟合得到的参数联合后验分布作为新数据加入时的先验。本研究中参数联合后验分布不可解析，采用多维核密度估计方法得到近似分布，作为重新校正过程中的先验。

由于多种数据类型被应用于贝叶斯校正过程，不同数据类型观测误差不同，因此需要对似然函数进行分解。如对于树高导向曲线[式(2)]，似然函数被分解为：

p(θ|D)∝p(DTP|θ)×p(DPP|θ)×

p(DSA|θ)×p(θ)。

(9)

式中：DTP、DPP和DSA分别表示角规临时样地(temporary plot，TP)、矩形固定样地(permanent plot，PP)和解析木(stem analysis，SA)中的观测数据，此时的p(θ|D)表示综合考虑多种数据类型(multi-type/multi-source data)的参数后验概率。

考虑到林分调查中观测误差的不稳定性，同时异常值很难有明确的判别标准，本研究采用重尾正态分布概率密度函数描述误差容易受异常值影响而导致有偏的估计(Siviaetal.， 2006)：

(10)

式中：σi为噪声尺度因子，用于描述第i次观测随机误差的不确定性；Ri为第i次观测值与对应模型预测值的离差除以σi。

林业调查数据的另外一个重要特征就是异方差，即观测值偏离均值的程度会受其他因素影响而非恒定。这种异方差特征一方面违反大部分经典统计学假设，另一方面也导致模型预测中错误的置信域估计。角规临时样地、矩形样地和树干解析信息需要依据噪声尺度因子σi进行融合，对于每种数据类型的每个响应变量，均需要分别拟合其误差分布。本研究假定观测误差的异方差性质为：

(11)

1.4 联立方程组估计下的参数联合后验概率密度

可变密度全林模型理论上应按1.2节介绍以特定顺序单独拟合，然而，由于全林模型内各预估模型经常会同时作为一个整体被使用，故本研究采用联立方程组形式构建模型，这就需要对似然函数进行调整。以1990年采集的角规临时样地数据拟合式(5)断面积预测模型为例，在方程式单独拟合时，其参数后验概率密度为：

p(c1,c2,c3,c4,gG,hG)。

(12)

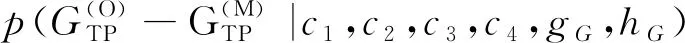
p(α,β,b1,b2,c1,c2,c3,c4,d1,d2,d3,d4,glnN,hlnN,gH,

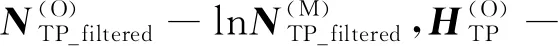
(13)

1.5 参数估计方法、收敛诊断与不确定性评估

由于参数联合后验概率分布不可解析，故本研究采用集成Metropolis-Hastings算法的Markov Chain Monte Carlo(MCMC)技术(Hastings， 1970； Metropolisetal.， 1953)模拟计算参数分布，并运用Gelman-Rubin收敛诊断技术(Brooksetal.， 1998； Gelmanetal.， 1992)确保MCMC收敛至正确的后验分布，该方法的优势在于整个过程既不涉及共轭计算，也不涉及条件概率和联合后验分布解析式的推导计算(Van Oijenetal.， 2005)。参数联合后验概率分布由MCMC的105次迭代生成，由于MCMC在开始阶段未收敛至后验分布，故将链的前10%作为“烧入”(burn in)舍弃掉(Gilksetal.， 1996)。平行运行3条MCMC链，计算其MPSRF(multivariate potential scale reduction factor)，该值较低时，代表不同起始值的子链最终独立收敛至相同的后验分布。本研究设定MPSRF接受阈值为1.05，是一种相对严格的收敛诊断标准(Brooksetal.， 1998)。

不确定性评估采用Monte Carlo抽样方法进行计算。试验中截取MCMC记录的后1/2，每隔10条记录抽取1组参数，每条子链得到5 000组参数值，3条子链共计15 000组参数值。尽管参数联合后验概率分布无法被解析，但无论是参数的边际分布、相关性矩阵、标准差等信息，还是预测的贝叶斯可信区间，诸多不确定性指标均可直接通过该样本计算获得。后续计算采用多维核密度估计方法得到近似分布，作为重新校正过程中的先验，该过程通过R工具包“BayesianTools”实现(Hartigetal.， 2019)。

采用Sobol指数量化分解各参数不确定性对最终预测不确定性的贡献(Caribonietal.， 2007； Saltellietal.， 2008)。该方法可将不确定性分解到任意参数组，通过考虑参数相关性后单个参数所贡献的总效应(STi)对不确定性传递过程进行评价，相应计算公式为：

(14)

式中：x-i表示给定除xi以外的所有模型参数；Y表示模型输出变量。

基于Monte Carlo输出结果可用于计算上述指标(Ioossetal.， 2020)。

各数据集本身规模不同，本研究采用自举法分析数据规模对模型预测不确定性的影响。选取临时样地这一数据集，因为数据集涵盖林分条件，更为多样化。依次设置样本数量N的规模为10、20、30、…、200块样地，进行以下计算： 1) 有放回的重抽样，样本数量为N； 2) 基于抽取到的样地数据对模型参数进行拟合，采用拟合结果进行预测； 3) 重复1、2过程1 000次。

2 结果与分析

2.1 不同时期调查信息的动态融合

区别于经典回归参数符合正态分布的假设，本研究贝叶斯方法获得的参数分布是不可解析的。尽管参数后验分布并不严格对称，但除个别参数呈明显偏态分布外，整体而言均值与最大后验概率估计值(maximum a posterior estimates,MAP)相差极小(表3、4)。图2以参数b1为例，展示了随着新数据加入参数边际分布不断更新的过程。树高生长的上渐近线参数b1(树高生长极大值)随着新数据加入不断升高，不确定性逐步降低；同时，参数b1与b2存在较高相关性，且其联合分布表现出明显正向关联(图3)，随着数据更新，联合分布峰值逐渐升高，参数不确定性也随之下降。

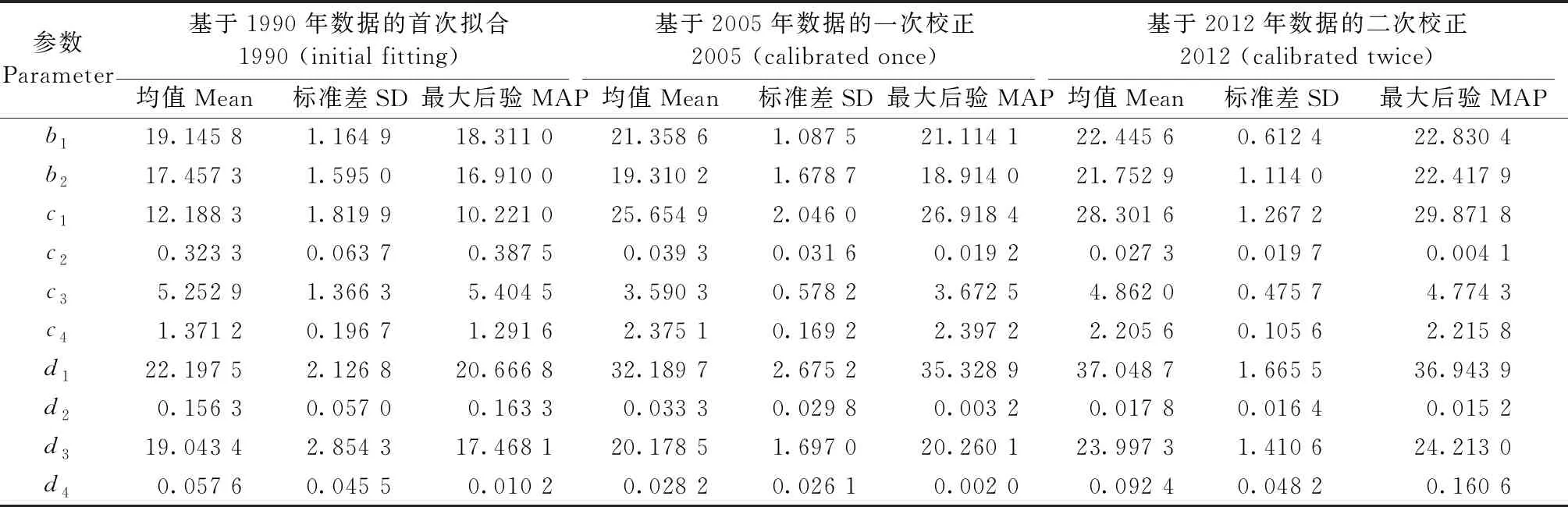
表3 参数循环更新过程中后验概率密度分布的变化①

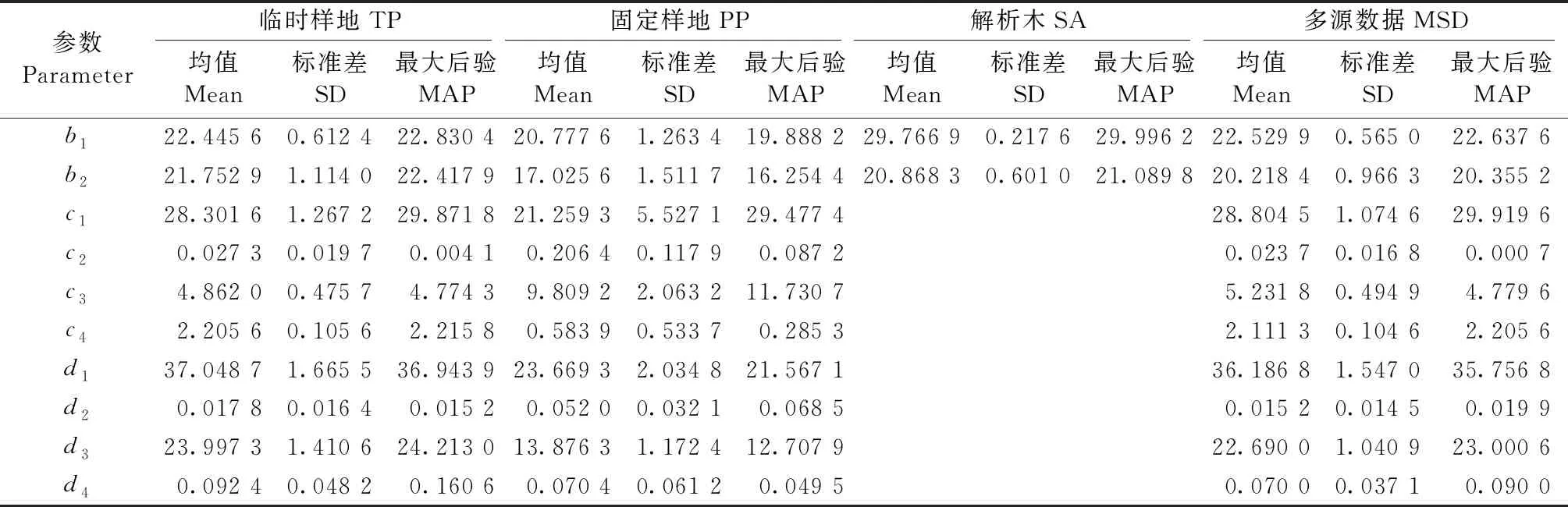
表4 基于多源数据的参数后验概率分布

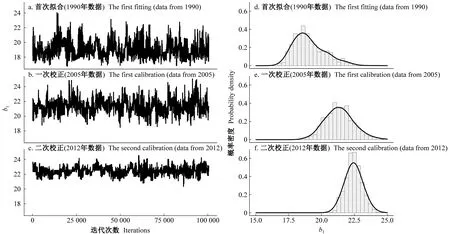
图2 马尔科夫蒙特卡洛迭代及参数b1后验概率密度的变化过程

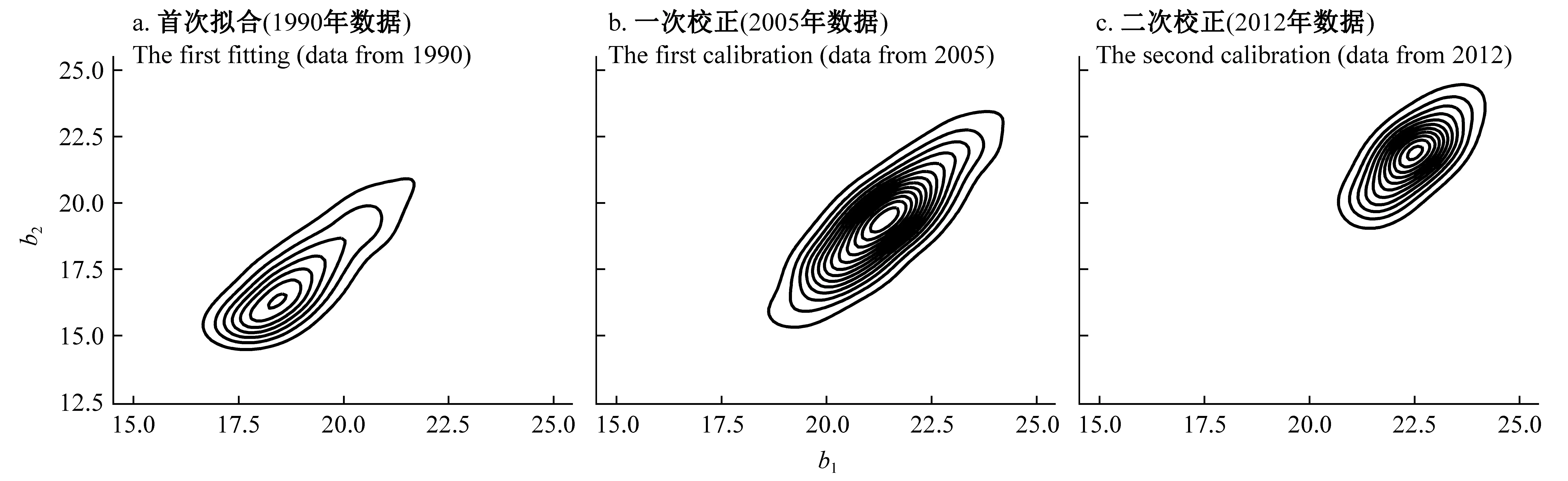
图3 循环更新中参数b1与b2的联合后验概率分布

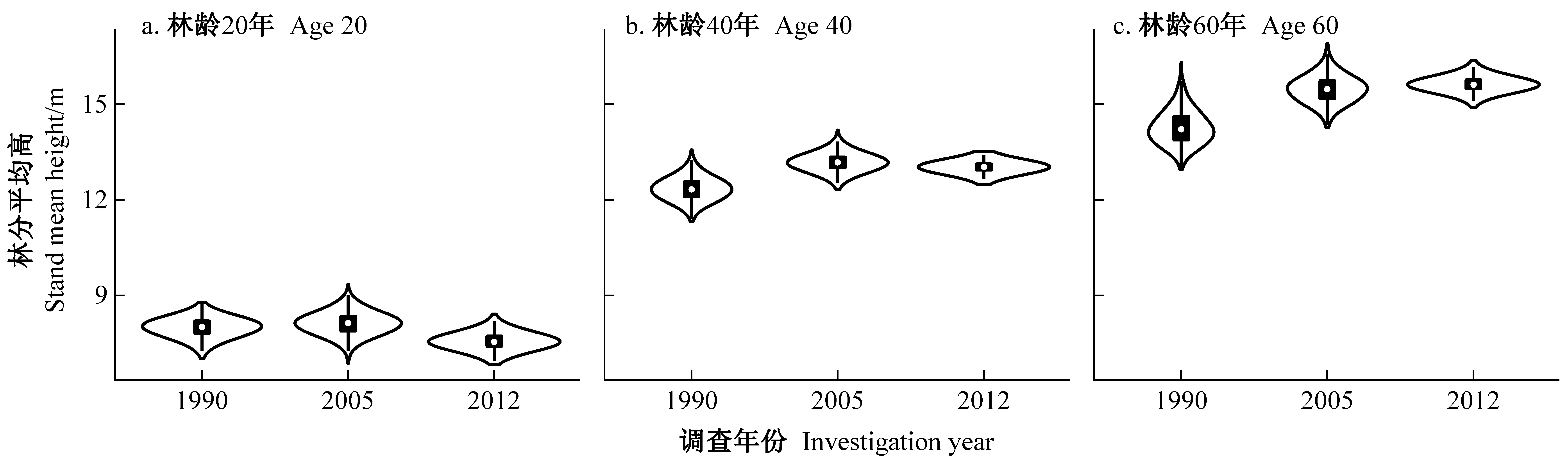
图4 林分平均高导向曲线在20、40、60年时的树高预测分布

随着参数概率分布改变，模型预测结果也随着新数据加入不断变化。贝叶斯框架下，参数不确定性最终会对预测的不确定性产生影响。基于1990年数据拟合模型预测的不确定性高于之后2次校正得到的模型(图4、5)。对于95%贝叶斯可信区间而言，基于1990年数据拟合的模型整个预测周期内树高导向曲线的平均不确定区间为2.3 m(图5a)，经2005年数据一次校正后不确定性下降至1.9 m(图5b)，而经2012年数据二次校正后不确定性下降至1.1 m(图5c)。同时，首次参数化时的模型在20年树高导向曲线估计中倾向于给出更高的幼龄林树高预测(图4a)和更低的成过熟林树高预测(图4c)。

林分动态预测过程中，数据与模型的关系是相辅相成的： 一方面，模型的开发和参数化需要基于数据； 另一方面，模型的表现也可直接反映数据特征信息。在数据信息融合与模型学习关系构建时，模型预测的最大概率曲线在幼龄林和成过熟林模拟上不断进行细微调整(图5)，模型对数据信息的不断吸收，更显著的作用是不断更新模型预测的不确定性。基于1990年数据进行模型拟合后，林分平均高、断面积和平均胸径的预测不确定性区间均在25～30年最低，而在其他年龄阶段的不确定性则相对更高(图5a、5d、5g)。经2005和2012年数据校正后，各龄阶的不确定性预测逐渐平衡。以林分平均胸径预测为例， 1990年数据对应最低不确定性出现在林龄25年(图5d)，经2005年数据一次校正，最低不确定性出现在林龄34年(图5e)，而经2012年数据二次校正，最低不确定性出现在林龄48年(图5f)。

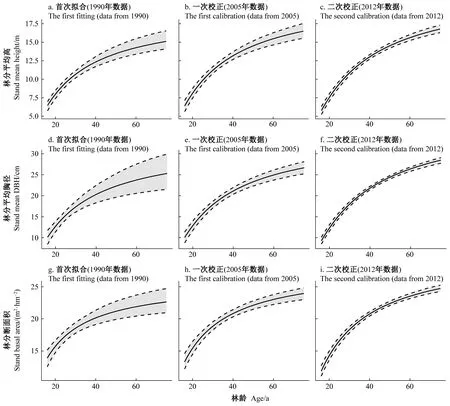
图5 林分平均高(导向曲线)、平均胸径和断面积预测的更新变化过程(SCI=11, SDI=600)

2.2 不同数据类型对林分模拟的影响

角规绕测临时样地、矩形固定样地、解析木数据在抽样原理、测量误差等方面的区别，导致模型参数拟合也存在差异。综合多种数据类型的模型校正基于多个似然函数相乘来描述数据与模型的关系，即同时考虑数据量和数据准确性对似然的影响。参数估计时，对于不同数据集中观测误差大小、变异幅度及其方差异质性的假设，会基于模型与数据的匹配程度进行自动调整，因此并不需要预设各数据集在总体似然函数中所占比重。单从边际分布考虑，综合多源数据的模型参数大多是对角规临时样地、固定样地和解析木对应模型参数的折中平均，且整体上与角规临时样地的拟合结果最为接近(图6e、6h)。相比样地调查，解析木数据倾向于给出更高的参数b1估计，即更大的树高极大值(图6g)。从联合后验分布角度来看，样地调查数据给出的参数估计比解析木参数有着更强烈的相关性(图7)。在树高导向曲线拟合中，林龄20年时几种类型数据给出的预测结果是相似的(图8a)，林龄40年(图8b)和60年(图8c)时基于解析木的预测则明显高于其他数据组。

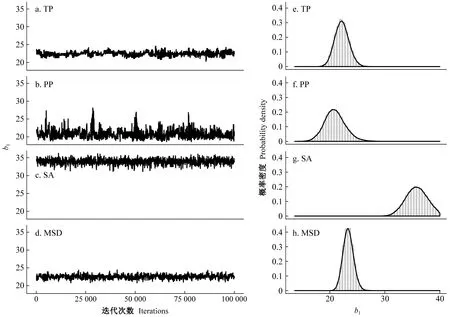
图6 不同数据类型中马尔科夫蒙特卡洛迭代及参数b1后验概率密度的变化过程

相比之下，基于多源数据构造的全林模型，在林分平均高、平均胸径和断面积预测中均表现出最低不确定性。固定样地数量远低于临时样地，调查年份均为2012—2015年，且多为坡度较缓的林分，这使得其在林分断面积生长预测和不确定性估计上与临时样地明显不同。基于固定样地的预测结果表明，林分断面积增长在林龄35年后并不会大幅减缓(图9e)，但这种预测也伴随着极高不确定性(±30.1%)。各参数对模型预测不确定性的贡献并不相同，断面积预测模型参数c4与胸径预测模型参数d4在式(5)和式(6)中传递的不确定性明显低于其他相关参数(表5)。同时，由于参数联合后验概率分布中参数相关性较高，各参数Sobol总效应指数加和后的数值也会远高于1。

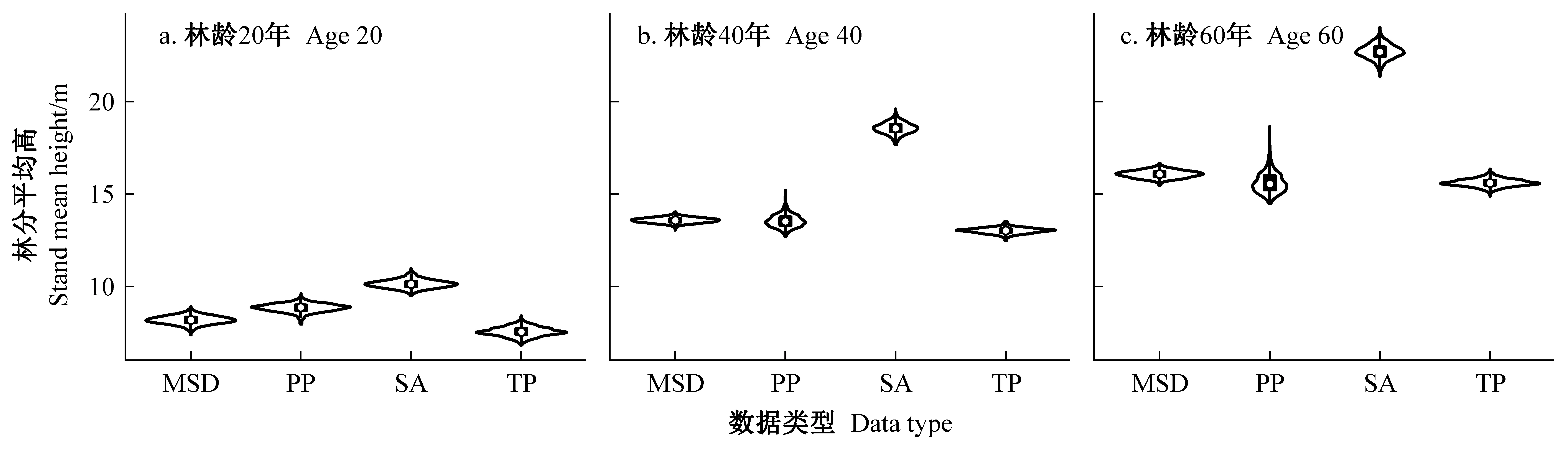
图8 基于不同数据类型林分平均高导向曲线在20、40、60年时的树高预测分布

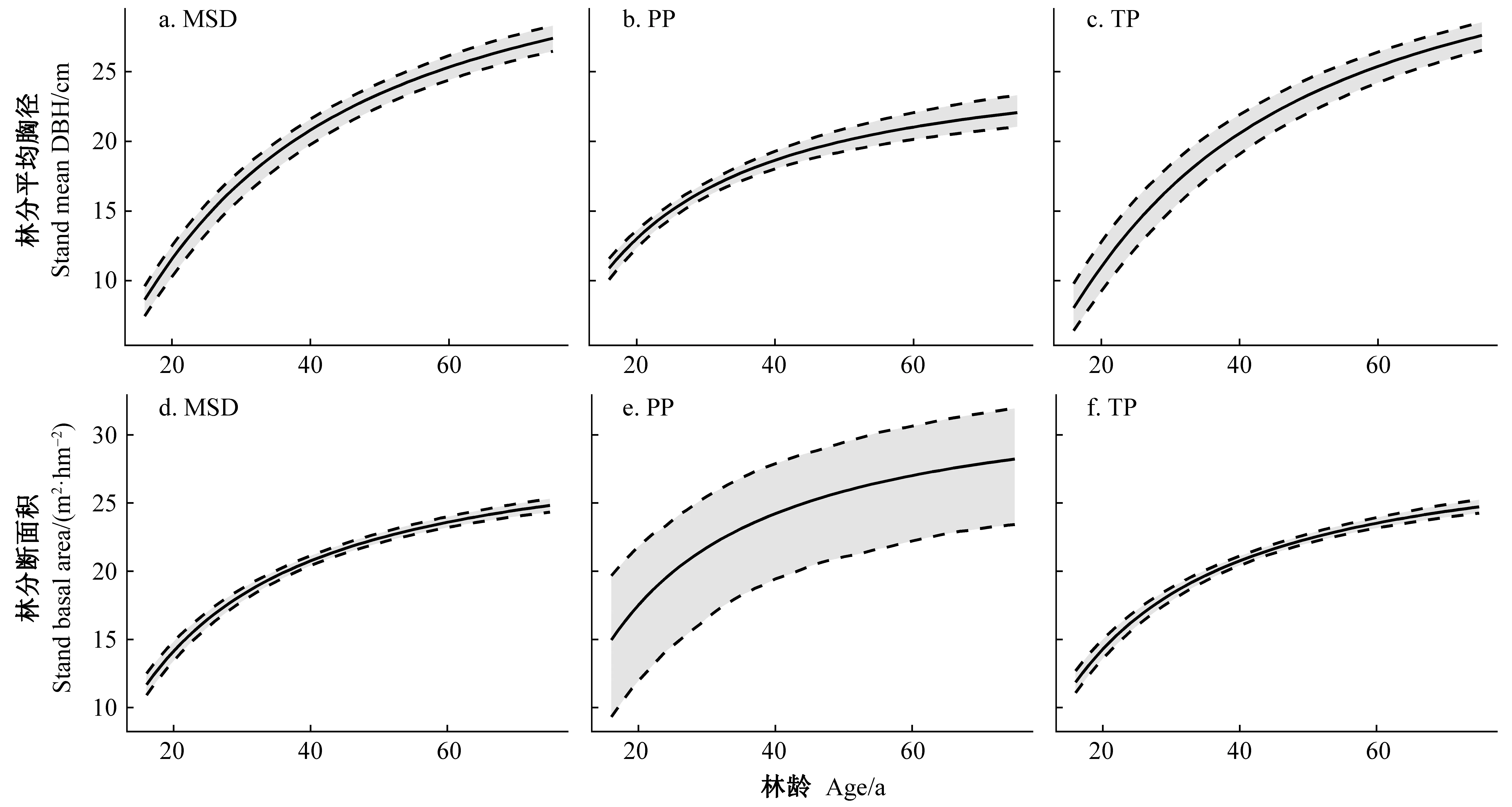
图9 基于不同数据类型的林分平均胸径和断面积预测的更新变化过程(SCI=11, SDI=600)

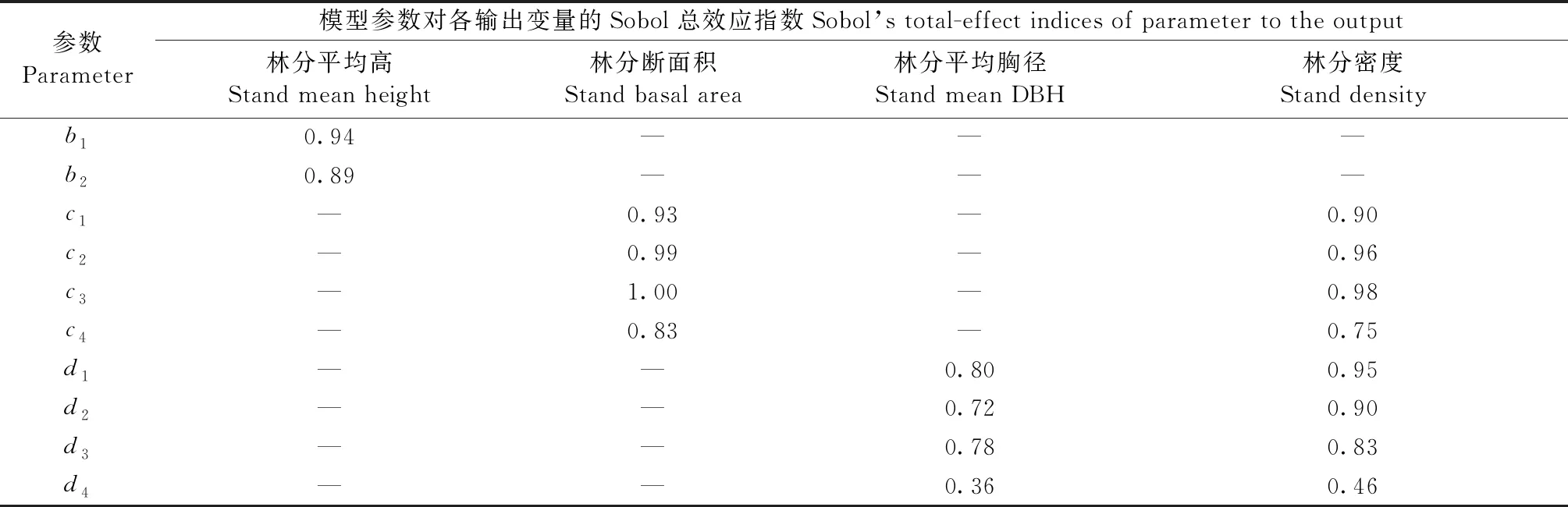
表5 基于方差的不确定性量化分解

模型预测的不确定性与建模数据本身规模直接相关。以林分断面积为例(图10)，当林龄为20、40、60年时，若抽选10块样地建模，1 000次重复后模型预测值波动标准差为1.77、1.40、1.90，而当样地数量增加至200块时，标准差则下降至0.44、0.27、0.30，这也直接解释了图9e中的较高不确定性实际是由固定样地数据量较小造成的。随着数据量增加，不确定性的降低速度逐步减缓，从10个样本增加至20个样本时，标准差减小14%； 从190个样本增加至200个样本时，标准差减小2%。

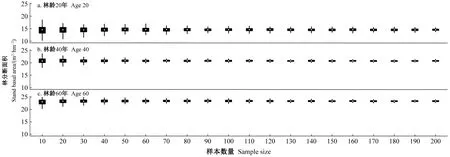
图10 随数据规模增加林分断面积模型预测不确定性的变化过程(SCI=11, SDI=600)

3 讨论

3.1 数据类型与抽样方法对林分模拟的影响

本研究涉及的几种数据类型各有其局限性，多源数据可避免某一数据类型缺陷过于严重传递至模型预测中。出于科研目的继而提供精准信息的固定样地长期观测数据有着极高的经济、人力和时间采集成本，通常可获取数据量较少，很难涵盖林分条件的变异幅度。临时样地成本低、数据量大，但与室内控制试验不同，野外调查临时样地数据无法满足抽样均衡性，即不能保证各年龄阶段样地的立地质量分布和变异是否相似，容易在某个龄阶出现有偏预测。解析木数据对林分整体状况的代表性很难保证。以树高生长为例，立地质量对林分生长动态具有直接影响，这意味着多源数据中的变异有特定比例可以被立地差异所解释。在林分平均高、平均胸径、断面积模型中，基于林龄和林分平均高得到的地位级指数被用作解释性变量，以描述不同立地条件下的林分生长收获差异。为减小立地评价的系统性偏差，树高导向曲线对抽样均衡性有着极高要求，即各年龄阶段样地的立地质量分布和变异应是相似的，且单个样地的立地质量在较长时期内保持一致。这些要求在多数情况下往往无法被完全满足。在树高导向曲线拟合中，解析木与样地调查数据在树木生长趋势描述上有着明显区别。理论上，解析木测量值比大多数树高调查方法都更加准确，且能够提供完整时间序列上的树高动态信息，因此在树高导向曲线中，本研究增加部分中等木和亚优势木的树干解析信息，以辅助解决幼龄林阶段数据不足的问题，同时避免各年龄阶段样地立地质量分布差异导致的系统性偏差。本研究涉及林分为相对同龄而非严格同龄林，林木间存在一定程度年龄差异，作为样本的中等木或亚优势木可能在生命周期中相当长的时间内处于被压迫状态，而在树高达到一定高度后从竞争压力中恢复过来(Hannetal.， 2002)。另外，解析木选取常常基于树木的干形和活力特征，这些都使得其树高生长趋势无法代表林分平均水平，且在成过熟林阶段产生一定程度的高估(图7g、7c)。当多源数据中不同数据集跨越较长时间尺度时，立地评价稳定性也会受多种因素影响，包括树木子代个体基因型的改变(Monserudetal.， 1990)、气候条件的改变(Bontempsetal.， 2009)、特定林分经营措施(Fox， 2000； Skovsgaardetal.， 2008)等。

尽管角规临时样地和矩形固定样地均按照森林经理调查时分层抽样与随机抽样相结合的准则设置，但在实际操作中，矩形固定样地常常会被主观建立在小班内坡度相对平缓的区域。相比之下，由于操作的便捷性，角规临时样地可以实现在平缓的下坡位和陡峭的山脊或陡坡均衡抽样，而山脊或陡坡的林分常常因土壤瘠薄等因素生产力较低(Schrothetal.， 2003)。角规调查的缺陷是林下灌木、幼树和地形等形成的复杂结构会造成绕测时视线遮挡(Van Laaretal.， 2007)。这些因素均会使得基于矩形固定样地的断面积生长量预测高于角规临时样地推算的结果(图9e、8f)。

3.2 不确定性的量化

复杂非线性模型回归分析通常被认为是优化问题。相比仅仅给出参数的最优估计值，贝叶斯方法通过MCMC抽样技术获得参数联合后验分布，使得模型中的信息可以更好体现在模型中。但即使是最优参数组合相同或相似，不同数据所给出的参数概率分布也可能存在很大区别，数据的异质性、观测误差、样本数量等会反映到参数联合后验分布中，并最终影响模型预测的不确定性。对比图5中2005和2012年数据组，或图7、9中临时样地和固定样地，最高概率曲线模拟的林分生长趋势非常相似，但数据中的信息(如不同龄阶时预测的可信区间)却并不相同。基于1990年数据的预测在林分成过熟林阶段有着很高不确定性，这是因为该阶段的观测较少且离散较高，而2005和2012年数据加入补充了成过熟林阶段的林分信息(图5)。大部分模型结果在林龄15～20年时均有着较高不确定性，这是因幼龄林阶段数据缺失造成的，尤其在林分断面积预测中最为明显(图9d、9e、9f)。整体而言，在不增加林分异质性信息的前提下，增大数据量是降低不确定性最直接的方法。相比林分平均高和平均胸径，林分断面积预测呈现出最高不确定性，且在数据量较低时差异尤为明显(图9e)。这说明对于林分断面积而言，降低不确定性所需的数据量和抽样调查的系统性都更高。影响林分动态的其他因素，如人为干扰、林型特征等，需要被更多地考虑到断面积模型构建中，无论是2.1节的多期数据更新，还是2.2节的多种数据类型比较，综合考虑全部信息的模型无论是参数还是预测均具有最高精度(最低不确定性)。

不确定性的解析式分解遵从Tylor展开式原理(Dietze， 2017)，贝叶斯方法以概率分布方式来描述参数和模型预测，由于本研究涉及的参数后验概率分布不可解析，不确定性评估以Monte Carlo抽样方法进行计算。需要强调的是，本研究涉及的数据和模型都较为简单，因而只考虑了参数不确定性对预测的影响，并没有涉及数据、模型结构、模型链接等部分的不确定性及其传递关系。在复杂模型的组合应用中，不确定性的传递与解构则是理解模型预测结果的关键性信息(Lebaueretal.， 2013)。

3.3 先验的设计

不同于过程机制模型，经验模型参数本身没有实际生理学意义，很难给出准确合理的先验设定。本研究没有探讨何种先验是“好的先验”，实际上讨论的先验都是基于以往数据信息，即基于往期数据得到的后验作为模型更新时的先验。以1990年数据进行首次拟合时，采用无信息先验，即等同于极大似然：

p(θ1990|D1990)∝p(D1990|θ1990)。

2005年数据的模型校正，以1990年模型后验作为先验，即：

p(θ2005|D2005)∝p(D2005|θ2005)×p(θ2005)∝

p(D2005|θ2005)×p(θ1990|D1990)∝

p(D2005|θ2005)×p(D1990|θ1990)。

2012年数据的模型校正，以2005年一次校正模型后验作为先验，即：

p(θ2012|D2012)∝p(D2012|θ2012)×p(θ2012)∝

p(D2012|θ2012)×p(θ2005|D2005)∝

p(D2012|θ2012)×p(D2005|θ2005)×p(D1990|θ1990)。

当模型完成基于2012年数据的二次校正后，参数后验同时包含1990、2005和2012年的数据信息。在这一模型循环更新框架下，如果有明确证据表明1990年数据不该作为2005年数据的先验，那么就意味着这2期数据中有1期是错误的且应直接将其舍弃，但通常情况下，随着数据积累，模型可靠性会逐步升高，新数据涵盖了新的或更复杂的林分状态信息。2005年数据校正和2012年数据校正模型变化幅度更小，则说明新增加数据提供的额外信息很少，不需要再投入过高成本对这些变化微小的变量继续收集数据。本研究采用重尾正态分布降低异常值对模型拟合的影响，各期数据似然结构相互独立，以避免精确数据被粗糙数据所稀释。贝叶斯方法被广泛应用于工程与信息科学的重要原因之一在于其高效的模型学习框架，这种高效性体现在当获取到新一期数据对模型参数进行更新时，并不需要对新获取数据的规模有任何特定要求(甚至1个观测点即可)，模型更新也不需要重新提取整理往期数据，因为往期数据信息已包含在先验中。

3.4 数据-模型关系

森林生态系统研究是一个渐进的过程，模型在该过程中至关重要。将已知信息作为先验并与未来可能获得的数据相结合，从而得到后验和预测分布(Westetal.， 1997)，随着数据积累逐渐更新对林分动态的理解，这一过程即数据-模型融合过程，其目的是使模型不断吸收新的信息(Clark， 2007)。

模型的准确性和适用范围取决于建模数据本身。理想情况下，模型构建和数据收集是不断迭代的过程，模型设计决定数据需求，进而决定外业调查内容和方式； 然而森林生长周期漫长，获取全部必要信息亦需漫长观测周期，同时，选用不同数据也会对模型拟合造成明显差异(Raulieretal.， 2003)，数据的类型、尺度、质量和规模等因素对模型构建与基于模型衍生的推论都有着重要影响。森林资源连续调查中，每一次调查分析结果都是下一次调查分析的最合理先验(张雄清等， 2014)。森林生长收获模型开发常常需要收集多个数据集信息，不同来源的数据在抽样设计、观测误差和观测数量等方面都会有所区别，而这些信息很难反映在模型的一组最优参数上。随着信息数据加入，模型改变也并不局限于最优参数组合的调整。综合考虑各数据组的误差分布、异方差等问题，需要模型开发者针对不同数据集采用独立的似然结构[式(9)]，不是简单地将数据进行混合。而在数据不断更新、模型学习并升级过程中，参数联合后验分布不断改变(图2和3)，进而导致预测的不确定性也在不断发生变化(图4和5)。在这种贝叶斯数据-模型框架中，数据与模型之间以概率分布形式融合为信息交互的循环体系。

本研究分析是基于贝叶斯框架下全林模型以联立方程组方式进行参数估计的结果[将式(1)和式(3)代入式(5)和式(6)后进行联立]，由此导致模型误差的传递，即地位级指数模型和林分密度指数模型存在误差，之后又将误差引入林分断面积和平均胸径模型中。贝叶斯框架下联立方程组比单独拟合有着更为复杂的似然结构[式(12)、(13)]，相应地，模型开发者可以根据自身对数据和模型的理解来调整误差分布和异方差假设，在拟合生长收获模型参数的同时获得描述误差分布的参数估计值[式(10)、(11)]。联立方程组模型中常见处理变量误差和异方差的方式之一是进行对数转换(洪玲霞等， 2012)，但对变量进行对数转化本身并没有生态学或生理学解释，同时，基于模型输出结果对变量进行逆向变换后预测结果也常常是有偏的(Dietze， 2017)。Zellner(1962)的似乎不相关联立估计在考虑不同方程误差项相关性的同时，也兼顾了异方差性问题，但较难与本研究的贝叶斯框架兼容。贝叶斯框架下进行似乎不相关回归和联立方程组回归通常会围绕基于协方差矩阵对联立后参数条件概率与联合后验的推导计算(Andoetal.， 2010)，本研究完全依赖于集成Metropolis-Hastings算法的MCMC技术来实现对联合后验分布的抽样和估计，从而最终实现将式(1)和式(3)代入式(5)和式(6)后所获得联立方程组的参数估计过程。考虑误差传递的另一个重要方法是度量误差效应模型(唐守正等， 1996； 1998)，该模型在贝叶斯框架下亦可实现(Clark， 2007； Clarketal.， 2007)，不仅地位级指数和立地指数评估的误差在胸径和断面积模型中传递，而且森林调查中的胸径、树高、断面积观测误差也可以被考虑。本研究所涉及的参数不确定性及其对预测不确定性的影响，仅仅只是不确定性或误差分析的一部分内容，同时受限于数据规模和质量，在测试数据代表性和描述模型开发中不确定性传递上仍有诸多不足。

本研究采用贝叶斯数据-模型框架，出发点是为了兼顾不同数据集所具有的不同抽样和观测误差，进而对不确定性进行量化。贝叶斯框架将模型校正和预测中的所有要素以概率分布方式进行处理(Clark， 2007； Dietze， 2017)，能够方便实现以上目标。但需要强调的是，贝叶斯并不是实现这些目标的唯一方法，多源数据的观测误差处理可通过若干似然函数相乘或权重法设置目标函数来实现(Marleretal.， 2010)，抽样方法的系统性误差也可通过多层级的混合效应模型来评估(Bijleveldetal.， 1998； Wareetal.， 1996)，不确定性的量化则可依赖于自举法来实现(Efron, 1979)。

4 结论

本研究以全林模型更新为例，描述贝叶斯框架下建模数据累积与生长模型不确定性循环学习的信息融合过程。结果表明，随着森林调查数据不断积累，模型参数和预测不确定性逐渐下降。建模数据信息中存在的缺陷可被量化并以不确定性方式直接反映在模型参数和预测中，进而为下一步模型改进与数据采集指明方向。多源数据的使用弱化了单一数据源中非均衡抽样和异常观测误差对模型的影响，可有效提高林分动态预测质量。这种数据-模型循环更新和兼容多源数据的贝叶斯框架，同样也适用于森林建模研究的其他诸多方向，如森林生产力、森林立地质量以及进界、自疏伐等森林动态与不确定性的研究和应用。