自反馈项对时滞神经网络系统稳定性的影响
2021-04-10王婷婷赵东霞范东霞
王婷婷, 赵东霞, 毛 莉, 范东霞
(中北大学理学院, 太原 030051)
时滞神经网络有着丰富和复杂的动态行为,其稳定性等问题受到国内外学者的广泛关注,取得了一系列有价值的成果和方法[1-3].文献[4-5]针对带有自反馈的四神经元时滞环状网络模型建立指数型多项式的特征方程,采用特征根分析方法找出具有负实部特征根的参数条件,这一方法在时滞系统的稳定性方面有广泛的应用.文献[6-7]研究的环形神经网络系统不含有自反馈项,其着重考察小世界联接对系统稳定性的影响,结果表明,小世界联接能看作一个“开关”,它可以控制系统的动力性能.文献[8]研究的环形神经网络系统含有自反馈项,但不含小世界联接,在Lyapunov方法的基础上,研究了系统平衡点的渐近稳定性,得到了保证神经网络全局稳定性的时滞相关准则,得出了一些系统动力学行为的相关结论,如Hopf分叉,以及混沌等.文献[9]研究了带有两个小世界联接的四神经元环形网络系统的Lyapunov稳定性,但没有考虑自反馈项以及自反馈权值对系统稳定性的影响.
受上述文献启发,本文研究如图1所示的时滞环形神经网络系统:

图1 具有自反馈的四神经元环状网络结构Fig.1 A four-neuron loop network with self-feedback
i=1,2,3,4,
(1)
其中,xi(t)指的是第i个神经元在t时刻的响应,k>0为神经元的增益,f(μ)=tanh(μ)是神经元的激活函数,τ>0代表时滞值,bij代表第i个神经元与第j个神经元之间的联接权值.显然,联接权值所构成的方阵B为:
(2)
特别地,b11,b22,b33,b44表示各个神经元的自反馈权值,b31和b24表示系统的两个小世界联接权值.
1 系统(1)与时滞相关的稳定性分析
考虑到双曲正切函数的有界性-1 (3) 则有 (4) 因此,对于充分大的时间T,当t≥T>0时,有|xi(t)|≤Pi. 定理1如果神经元的联接权值bij与增益k满足如下条件: (5) 那么,系统(1)的平凡解是全局渐近稳定的,其中, (6) 证明首先构造如下Lyapunov函数: (7) 则对于x1,x2,x3,x4∈,W连续且非负,函数W对时间的右导数为 (8) 因为 f(xi(t-τ))-f(xi(t)), 且考虑到 f(xi(t))xi(t)≥f2(xi(t)),a2+b2≥2ab, 那么(8)式可化为 D+W|(1)≤ (9) 考虑到0≤f′(μ)=(tanh(μ))′<1,则可对(9)式的第二部分进行放大, 因此有 (10) 其中,Φi与Qj的定义见(6)式,且 (11) 同样的,再定义如下Lyapunov函数: (12) 根据拉格朗日中值定理以及激活函数f(μ)=tanh(μ)及其导数的性质可得 f(xi)=xi(t)f′(ηi),ηi∈[0,xi(t)], (13) D+V|(1)≤Φ1f2(x1(t))+ Φ2f2(x2(t))+Φ3f2(x3(t))+Φ4f2(x4(t))+ U2f2(x2(t))+U3f2(x3(t))+U4f2(x4(t)), (14) 其中,Ui(i=1,2,3,4)如(5)式所示. 综上可得,当U1,U2,U3,U4<0时,D+V<0,那么V(t)≤V(0).因为xi(t)(i=1,2,3,4)在[-τ,∞)上也是有界的,故得xi(t→∞)=0. 由定理1可得如下关于时滞τ的稳定性结论. 定理2若bij与k满足如下不等式: (15) 则可定义一个新的时滞值: (16) 当时滞τ满足0≤τ<τ*时,系统(1)的平凡解是全局渐近稳定的. 下面考察自反馈项对系统稳定性的影响. 由(6)式可得 (17) 显然有 M1||b11|=|b22|=|b33|=|b44|=0< M1||b11|,|b22|,|b33|,|b44|不全为0. (18) 同理, Mi||b11|=|b22|=|b33|=|b44|=0< Mi||b11|,|b22|,|b33|,|b44|不全为0,(i=2,3,4). (19) 此外, -Φi||b11|=|b22|=|b33|=|b44|=0> -Φi||b11|,|b22|,|b33|,|b44|不全为0, (i=1,2,3,4). (20) 故 τ*||b11|=|b22|=|b33|=|b44|=0> τ*||b11|,|b22|,|b33|,|b44|不全为0,(i=1,2,3,4). (21) 从而可以得出下列定理3. 定理3随着自反馈项的增加,时滞τ的全局稳定性区间逐渐变小. 考虑到tanh′(0)=1,因此系统(1)的线性化方程的矩阵形式为 (22) 在这一部分,为方便推导,不妨假设b11=b22=b33=b44=b,即矩阵B为: (23) 此时,矩阵B的特征方程为: b12b23b34b41=0. (24) 令 (25) 则(24)式可化为 λ4-4bλ3+6b2λ2-(4b3+p)λ+b4+bp-q=0. (26) 令λ=kμ,那么(26)式等价于 (4b3k-3+pk-3)μ+(b4+bp-q)k-4=0. (27) 引理1[10](推论2.3和推论2.7) 矩阵B的特征值di满足di 引理2[11](Schur-Cohn准则) 实系数多项式 F(μ)=anμn+an-1μn-1+…+a1μ+a0,an>0 的全体根位于单位圆内,当且仅当 且(n-1)×(n-1)阶Jury矩阵 的内子矩阵的行列式均大于0. 结合引理1可得,对任意的时滞τ,系统(22)渐近稳定,当且仅当方程(27)的根满足|μ|<1,即位于单位圆内.从而结合Schur-Cohn准则可得系统参数的稳定性条件. 定理4对任意的时滞τ,系统(22)渐近稳定,当且仅当系统参数k,b,p,q满足如下四组不等式条件: (28) 证明F(μ)的全体根位于单位圆内,当且仅当: F(1)=1-4bk-1+6b2k-2-4b3k-3- pk-3+(b4+bp-q)k-4>0, (29) 4b3k-3+pk-3+(b4+bp-q)k-4>0, (30) 且3×3Jury矩阵 的内子矩阵的行列式均大于0.由于 1+6b2k-2-16b4k-4-4pbk-4-16b6k-6-8pb3k-6-p2k-6, 1-6b2k-2+16b4k-4+4pbk-4-16b6k-6-8pb3k-6-p2k-6. 在这一部分,主要结合数值仿真来阐述自反馈项对系统(1)稳定性的影响. 例1考虑系统 (31) 即k=3,联接矩阵B为: 首先,令自反馈项全为0,即|b11|=|b22|=|b33|=|b44|=0.经计算得: U1=Φ1+τM1=-2.7+ 于是, 接下来,考虑自反馈项不全为0的情况. 1) 只有一个自反馈项不为0,不妨取|b11|=0.3,|b22|=|b33|=|b44|=0,经计算可得: U1=-0.27055<0,U2=-1.87594<0, U3=-1.91961<0,U4=-1.70459<0, τ*=1.12705. 2) 有两个自反馈项不为0,不妨取|b11|=0.3,|b22|=0.1,|b33|=|b44|=0,经计算可得: U1=-0.25555<0,U2=-1.43289<0, U3=-1.91461<0,U4=-1.69959<0, τ*=1.11917. 3) 有三个自反馈项不为0,不妨取|b11|=0.3,|b22|=0.1,|b33|=0.2,|b44|=0,经计算可得: U1=-0.24555<0,U2=-1.42289<0, U3=-0.99278<0,U4=-1.66959<0, τ*=1.11397. 4) 当自反馈项全不为0时,不妨取|b11|=0.3,|b22|=0.1,|b33|=0.2,|b44|=0.1,经计算可得: U1=-0.23555<0,U2=-1.41789<0, U3=-0.97778<0,U4=-1.21987<0, τ*=1.10883. 因此,根据定理1可得,在上述所有情形下,系统(31)的平凡解全局渐近稳定,并且时滞τ的稳定性区间随着自反馈项的增加而减小.图2展示了自反馈项全不为0时系统(31)的状态的收敛情况,其中,初始值为x1(0)=1,x2(0)=0.8,x3(0)=0.6,x4(0)=0.5. 图2 系统(31)解的渐近稳定性Fig.2 Asymptotic stability of the solution of system (31) 例2在系统(22)中,取k=1,联接矩阵B为: 根据(25)式计算可得p=-0.4,q=0.5,代入(28)式可解得 -0.029168 (32) 也就是说,无论时滞值取多少,只要自反馈权值b满足(32)式,该系统总是渐近稳定的.图3展示了b=0.1,τ=0.5,初始值为x1(0)=1,x2(0)=0.8,x3(0)=0.6,x4(0)=0.5时系统状态的收敛性. 图3 系统(22)平凡解的渐近稳定性Fig.3 Asymptotic stability of the solution of system (22) 本文研究带有自反馈的四神经元时滞环形神经网络系统的数学模型,首先采用Lyapunov方法进行全局渐近稳定性分析,得出了系统稳定时,各参数的条件,时滞τ的范围,得到了与时滞相关的稳定性结论.结果表明,自反馈项的增加使得时滞τ的全局稳定性区间缩小.另一方面,采用Schur-Cohn准则得到了与时滞无关的稳定性结论,并通过数值例子给出了自反馈项的取值范围.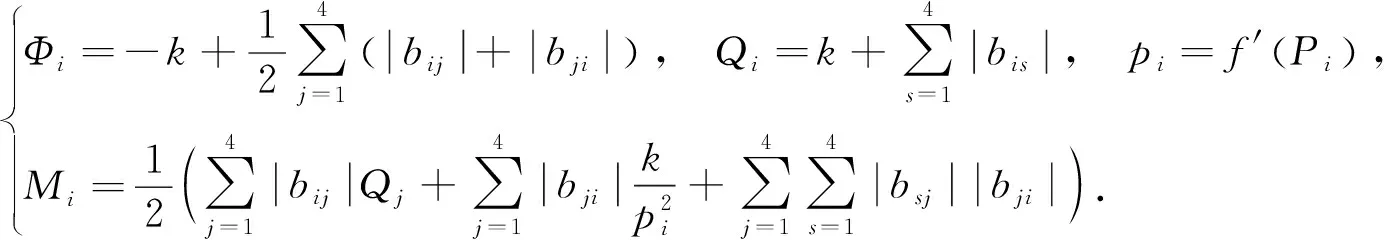

0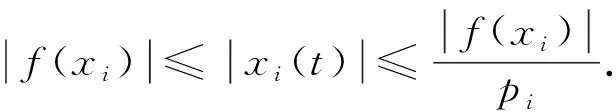
2 系统(1)与时滞无关的稳定性分析
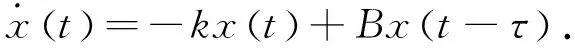


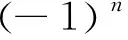





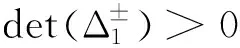
3 数值仿真
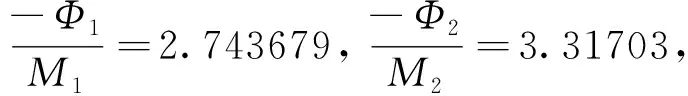

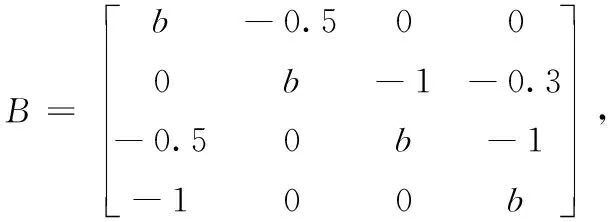

4 结论
