基于GPU的多相信道化算法效率分析与应用
2021-04-09陈永强党宏杰焦义文刘燕都
陈永强,马 宏,党宏杰,焦义文,刘燕都
(1.航天工程大学 电子与光学工程系,北京 101416;2.北京通信与跟踪技术研究所,北京 100094)
0 引言
多相滤波器组(Polyphase Filter Bank, PFB)是数字信号滤波抽取的一种高效实现结构,利用该技术可将串行的信道化过程分解为并行的多路处理流程,从而提高数字信号处理效率[1]。1991年,SETI首次将PFB引入射电系统并使用该技术设计了频谱分析仪[2],此后,PFB被越来越多地用于信号处理数字后端,目前国际上多个重要系统均使用了PFB技术进行观测频谱的信道化[3]。
20世纪60年代,美国Geraid.Estrin[4]率先提出可重构计算(Reconfigurable Computing)概念。该技术核心思想在于,在通用平台上通过系统软硬件结构的灵活重构实现不同的功能[5-6]。图形处理器件(Graphic Processing Unit, GPU)由于具有众多的运算核心,特别适合于大量数据的并行处理,2007年NVIDIA提出的计算统一设备架构(Compute Unified Device Architecture, CUDA)从软件和硬件层面大大简化了基于GPU的系统开发流程,使得GPU在通用计算领域得到更为广泛应用。当前,由于GPU相较于FPGA能够实现较高的频谱高分辨率且具有更高的可重构性和扩展性[4],基于CPU+GPU的异构信号处理系统在射电天文[7-8]、雷达[9-10]、无线通信[11-12]等众多领域成为研究热点。
随着基于GPU的高性能计算(High Performance Computation,HPC)技术的快速发展,基于GPU的PFB系统研究逐渐受到研发人员的重视。2011年,麻省理工学院Haystack天文台的Mark[13]使用NVIDIA Tesla C2050 GPU设计了一款用于VLBI 数字采集系统RDBE的PFB系统,验证了用GPU替代现有的FPGA板信号处理系统的可能性。测试结果显示,系统实时数据处理速率达到890 MB/s,而且随着GPU技术的进一步发展,系统的处理能力将进一步提升和扩展。2014-2016年,马里兰大学的Scott C. Kim等研究了基于GPU的多载波系统低延迟多速率重信道化器[14-16]和宽带接收机[12],该团队利用GPU多层次线程结构和存储结构对PFB的实现进行了优化,采用时域卷积和高维线程模型,在数十兆赫兹带宽内实现了2G、3G和4G无线电通信信号的高效信道化,系统具有设计灵活、软件重构、低延迟和高数据吞吐量等优点。2017-2018年,Simon Faulkner等基于GPU开发了一款射频频谱感知截获系统,并为该系统研发了信道化设备[17-18]。该系统采用多相滤波结构实现宽带信号的信道化接收,采用CUDA stream对流程进行了并发优化。最终,系统处理带宽达到500 MHz带宽,可实现1.333 Gs/s采样率的实时信道化处理能力。该文献提出的信道化器是一种比较成熟的PFB结构。2017年,新疆天文台[8]为其观测系统设计了基于GPU的多相滤波系统,为GPU在国内数字后端应用进行了有效的探索。
在多相滤波系统中,FIR滤波环节由于涉及大量数据的乘加运算,是影响系统效率的关键因素。当前,在GPU平台上FIR滤波算法的实现方式主要分为频域滤波算法[19]和时域滤波算法[20]2种。文献[21-22]给出了基于FFT的频域FIR滤波方法的实现方式,得到了较好的加速比,同时对比了GPU、Intel-ipps和FFTW三个平台上长序列频域滤波效率,证明Intel-ipps性能略优于FFTW。而Scott C. Kim[12]、Mark[13]及Jayanth Chennamangalam[23]等均从时域实现了多相滤波过程,给出了时域FIR在连续信号滤波中的应用。以上文献分别从时域和频域给出了长序列FIR滤波的优势和实现方法,却没有给出在不同的应用场景下2种滤波算法的适用条件。另外,近年来,在基于FPGA的平台上,基于DA法[24-25]和查找表法[26]等多种优化方法的高效并行FIR滤波方法研究取得丰硕成果,但这些方法难以直接移植到GPU平台。
本文首先介绍了基于多相滤波技术的并行信道化算法,并分析了其运算效率;然后对运算过程中耗时最长的多通道并行滤波过程进行了分析,基于CUDA流式架构分别设计了基于时域卷积和频域快速卷积的FIR滤波算法,并分析了2种算法在多相信道化结构中的性能;最后基于GPU平台设计了多相信道化实现方法并用实验验证了分析的正确性。
1 基于多相滤波技术的并行信道化算法
典型的K通道并行信道化算法低通滤波实现原理框图如图1所示[27]。

图1 多通道基带转换原理框图Fig.1 Block diagram of multi-channel baseband conversion
图1中,各信道中心频率为ωk=2πfk/fs,由于实际处理过程中所用均为实信号,因此本文重点针对实信号进行分析。设经过D倍抽取后,输出采样率为fs2=fs/D,采样周期Ts2=DTs1,在实信号模式下,该结构第k通道数学表达式为:
yk(mTs2)=x1(nTs1)e-jωkn*hLP(nTs1)|n=mD|=
(1)
为了提高运算效率,对滤波过程进行多相分解,将滤波器分解为并行的K路,每一路分支滤波器长L=[N/K]。原型低通滤波器索引i可分解为:
i=qK+p,
(2)
式中,q为每一路分支滤波器内部点数索引,q=0,1,2,…,L-1;p为分支滤波器索引,p=0,1,2,…,K-1。可得:
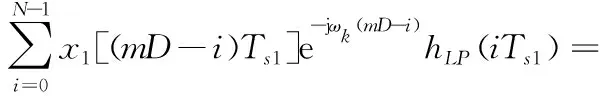
(3)
令hp(m)=hLP((mK+p)Ts1)表示第p路分支滤波器,xp(m)=x1[(mD-p)Ts1]表示并行分路后第p路输入信号。式(3)可改写为:
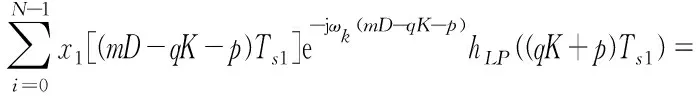
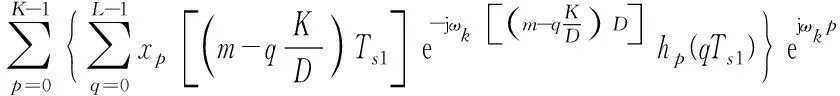
(4)
令h=K/D,i=q,l=qh,则有:


(5)

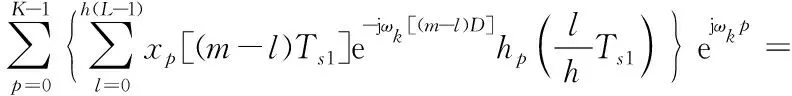

(6)
此时,实际上按照多相分支滤波器架构完成了中心频率为ωk的射频信号的单通道信道化滤波接收。由于各通道均匀划分,可令ωk=2πk/D,滤波器截至频率为π/D,则第k通道信道化后的信号可表示为:
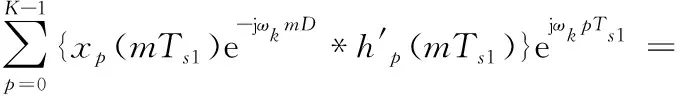
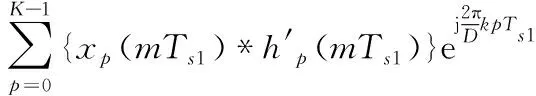
(7)
式中,为了最大限度提高处理效率,降低每个通道的数据速率,令抽取倍数D等于通道数K,即可得到最大抽取的DFT滤波器组:

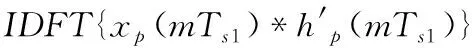
(8)
式(8)即为最大抽取DFT滤波器组的经典多相信道化结构的数学表示,也是干涉测量基带转换器、射电天文数字后端等系统常用信道化算法。该算法本质是多通道并行分支滤波和多路DFT,DFT可用其快速算法FFT实现,因此多路分支滤波运算效率成为制约该结构实时性的主要因素。由式(8)可知,分支滤波过程本质上仍然是多路FIR滤波过程,而对于长度为L的输入序列x(n),n=0,1,…,L-1和长度为M的FIR滤波器h(n),n=0,1,…,M-1,FIR滤波过程可用如下线性卷积关系表示:
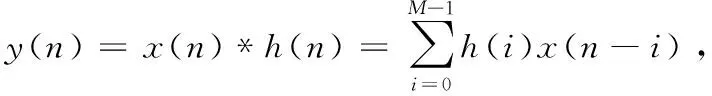
(9)
式中,y(n)为线性卷积输出,其长度为L+M-1。此时,问题转化为长序列FIR滤波的高效实现。
2 基于CUDA的长序列实时FIR滤波方法研究
在实际工程实践中,由于输入信号过长无法一次处理,通常需要做分段处理,但由于卷积运算本身特殊性,分段处理时在每一段数据两端位置将出现结果异常。为解决这一问题,研究者提出基于重叠相加法和重叠保留法[28]的长序列FIR滤波连续方法。马里兰大学的Kim等[12]利用卷积算法和重叠保留法在CUDA平台上实现了高效滤波运算,设计了基于GPU的宽带信道化接收机。为了提高卷积运算的效率,文献[21-22]也提出了重叠相加法和频域卷积相结合的快速滤波方法,并给出了该方法在CUDA平台上的应用效果。本节将重点根据并行信道化运算需求,设计适用于本文架构的高效滤波方法。
2.1 典型长序列滤波算法
为了实现长序列的连续滤波,需要对输入数据分段进行运算。而根据分段处理方法的不同,常用的长序列滤波方法分为重叠相加法和重叠保留法[29]。2种算法实现流程如下。
2.1.1 基于重叠相加法的长序列分段滤波方法
设长为N,输入数据x(n)每一段处理长度为L,滤波器h(n)阶数为M-1,那么该算法的执行流程为:
① 将输入数据分段,每段长度为L;
② 计算第1段数据与h(n)的卷积,得到滤波结果y0(n)长度为L+M-1;
③ 计算第2段数据与h(n)的卷积,得到滤波结果y1(n)长度为L+M-1;
④ 将y1(n)与y0(n)拼接作为输出,并使得y1(n)的前M-1点与y0(n)的后M-1点重叠相加;
⑤ 以拼接结果作为新的y0(n)并重复以上两步,直到分段数据处理完毕。
2.1.2 基于重叠保留法的长序列分段滤波方法
设长为N,输入数据x(n)每一段处理长度为L,滤波器h(n)阶数为M-1,那么该算法的执行流程为:
① 将输入数据分段,每段长度为L;


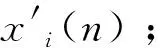
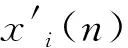
⑥ 以y0(n),y1(n),y2(n),…的顺序拼接结果即可得到滤波输出。
重叠相加法的优势在于对输入数据的操作简单,在分段方法确定后即可直接进行卷积运算,流程清晰,但完成卷积运算后各段结果数据之间增加了加法操作。重叠保留法需要对输入数据进行M-1点的循环拷贝,增加了数据传输的压力,但其输出数据直接为最终结果,无需额外操作。2种方法虽略有区别,但其综合运算复杂度相当[30],本文选择重叠保留法作为数据处理方法。
2.2 基于GPU的多通道并行时域滤波方法
由式(9)可知,对一个时间序列做FIR滤波本质上就是将该信号与滤波器单位冲激响应做线性卷积。输出信号实际上是以滤波器单位冲击响应为权值,对输入信号滑动求取加权和。在实时信号处理中,这一过程可以通过重叠保留法予以实现。GPU架构下基于重叠保留法的多通道并行FIR实现过程如图2所示。
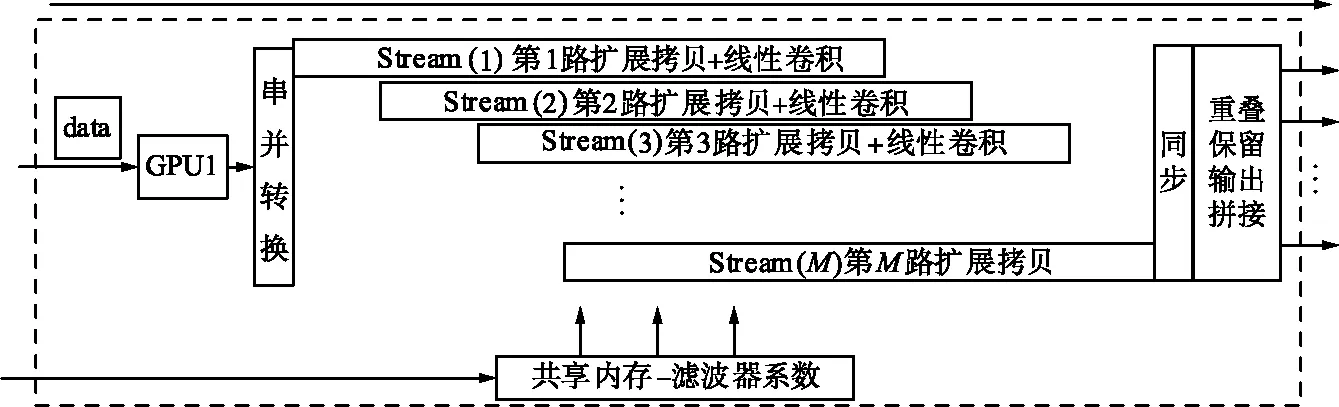
图2 基于重叠保留法的时域FIR滤波流程Fig.2 Time-domain FIR filtering process based on overlap preservation method
GPU架构下基于重叠保留法的长序列时域FIR滤波流程如下:
① 设参与滤波的数据为k路,定义并启动k路CUDA stream,保证每一个stream对应处理一路数据;
② 在每一个stream内,将输入采样信号x(n)用重叠保留法分块为xi(n),分块后每一段数据大小为L,滤波器长度为M,然后将第1段数据前向扩展M-1个点,使得其中扩展后数据长度为L+M-1;
③ 利用线性卷积分别计算第1段前L次滑动卷积过程,将L点结果输出至显存;
④ 将上一段后M-1点数据拷贝到下一段数据头部重新组成L+M-1点数据;
⑤ 重复③、④两步,计算每一段分块数据时域滤波结果yi(n);
⑥ 将yi(n)各段拼接整合,提取出整段数据最终的滤波结果。
2.3 基于GPU的多通道并行频域滤波方法
由傅里叶变换的原理可知,2个序列的DFT的乘积相当于该序列时域做循环卷积(或圆周卷积)。而根据文献[33]利用圆周卷积无混叠计算线性卷积的条件是,输出信号y(n)至少需要N点DFT,N≥L+M-1,即:
Y(k)=X(k)H(k),k=0,1,...,N-1,
(10)
式中,X(k),H(k)对应于x(n)和h(n)的N点DFT。由于输出信号y(n)的N点DFT一定可以在频域表示该信号,故利用DFT先求的输入信号和滤波器系数的N点DFT,然后在频域逐点相乘得到乘积序列Y(k),最后对Y(k)求N点DFT得到的圆周卷积,该圆周卷积结果等于x(n)和h(n)的线性卷积,即:
y(n)=x(n)*h(n)=IDFT[X(k)H(k)]=
IDFT[Y(k)],
(11)
式中,k=0,1,...,N-1;n=0,1,...,N-1。
以上方法给出了利用DFT实现线性卷积的过程,从公式和数据处理流程上看,与时域直接卷积方法相比,该方法增加了信号和滤波器系数时域扩展、DFT运算、频域乘法运算以及IDFT运算,流程更加复杂,但是与复杂的卷积运算相比,DFT和IDFT可以通过快速算法得到所需信号,极大地提高了运算效率。基于重叠保留法的频域FIR实现过程如图3所示。

图3 基于重叠保留法的频域FIR滤波流程Fig.3 Frequency-domain FIR filtering process based on overlap preservation method
GPU平台上基于重叠保留法的频域快速卷积算法流程如下:
① 设参与滤波的数据为k路,则定义并启动k路CUDA stream和FFT句柄,并将Cufft句柄绑定到stream;
② 将输入采样信号x(n)分段,第i段为xi(n);每一段数据长度为L,滤波器h(n)长度为M;
③ 将每一段数据xi(n)和滤波器系数h(n)扩展为L+M-1位。其中数据向前扩展M-1位,即在x0(n)前M-1位补零,此后在xi(n)前M-1位补xi-1(n)的后M-1位;在h(n)后向扩展L-1位并补零;
④ 利用Cufft库函数计算分段数据L+M-1点FFT,Xi(k)=FFT[xi(n)],同时对滤波器也做相同点数的FFT,Hi(k)=FFT[h(n)];
⑤ 将经过FFT运算的数据Xi(k)和滤波器系数Hi(k)对应相乘,得到每一段数据的滤波结果的频谱,Yi(k)=Xi(k)Hi(k);
⑥ 对滤波结果的频谱做L+M-1点FFT,yi(n)=IFFT[Yi(k)],即可得到分段数据长度为L+M-1的线性卷积结果yi(n);
⑦ 将yi(n)中后L点数据取出并按顺序拼接,即可得到整段数据的滤波结果。
2.4 2种滤波方法对比分析及实现
基于重叠保留法的频域滤波过程有效利用了FFT算法优势,在长序列高阶滤波过程中加速效果明显。然而,该方法将原本简单的乘加运算关系变成了变量扩展、分段FFT、相乘、分段IFFT等多个步骤,增加了流程的复杂度,给流程的调度带来了额外的开销,而且在滤波器阶数较少的情况下,在重叠部分需要额外增加大量的内存操作和运算,这些操作将直接影响算法性能;另外,为了使用FFT算法加速运算过程,数据长度也需满足2的整数次幂的要求。与之相比,时域滤波方法由于简单直接,在低阶运算中将具有更优的应用效果,但卷积运算本身的复杂性将导致时域算法在高阶滤波运算中效率急剧下降。下面用仿真方法对2种算法的运算复杂度进行分析。
设每一路输入数据分段长度为L,滤波器系数长度M,基于重叠保留法的时域和频域滤波算法的计算复杂度根据卷积和FFT算法的不同而有较大差异。下面以2种算法中耗时较长的乘法计算次数为参考,分析2种算法的运算复杂度。
2.4.1 时域卷积算法
在基于重叠保留法的时域滤波算法中,直接卷积运算将需要2×L×M次乘法运算;由于数据前向扩展M-1点,共增加约M(M-1)次乘法运算。所以采用基于重叠保留法的时域滤波算法需要的乘法运算次数为:
N=2ML+M(M-1)=M(2L+M-1)。
(12)
当数据长度与滤波器系数相当,即M≈L时:
N≈3L2。
(13)
当数据长度远大于滤波器系数,即M≪L时:
N≈2ML。
(14)
对比式(13)、式(14)可知,当滤波器阶数较少时,时域方法乘法运算量与数据长度近似成线性关系。随着滤波器阶数的增加,运算复杂度急剧增大,当滤波器阶数与数据长度相当时,乘法运算量与数据长度近似成平方关系。由此可见,时域卷积方法在低阶条件下将具有更大的优势。
2.4.2 频域卷积算法
当采用频域滤波算法时,需要首先对数据和滤波器系数进行扩展,使得2路数据长度均达到L+M-1点,然后对2路扩展数据做FFT运算,则FFT运算实际乘法运算次数为:
N=4×[(L+M-1)/2×lb(L+M-1)+(L+M-
1)/2×lb(L+M-1)]=
4×[(L+M-1)lb(L+M-1)]。
(15)
2个序列相乘需要经过L+M-1次乘法,得到L+M-1个结果,再对L+M-1点数据进行IFFT运算,需要2×[(L+M-1)lb(L+M-1)]次乘法。由此可知,采用频域卷积需要的乘法次数为:
N=6×(L+M-1)lb(L+M-1)+(L+M-1)=
(L+M-1)[6lb(L+M-1)+1] 。
(16)
当数据长度与滤波器系数相当,即M≈L时:
N= 2L[6lb(2L)+1]。
(17)
当数据长度远大于滤波器系数,即M≪L时:
N≈L[6lbL+1]。
(18)
2.4.3 2种算法对比
从以上分析可以看出,时域滤波方法过程简单,当滤波器阶数较少时,运算效率较高;但受卷积运算影响,当滤波器阶数较大时,单次运算量过大,难以满足要求。而频域滤波方法充分利用了FFT运算的高效结构,能够明显降低乘法运算次数,而且随着滤波器阶数的增加和处理数据点数的增加,这种优势将更加明显;但频域滤波方法在运算过程中需要对参与运算的滤波器系数和输入数据进行扩充,并在扩充的基础上开展2次FFT运算、一次逐点乘法运算和一次IFFT运算,给运算过程带来额外的负担,而且这种负担在滤波器阶数较低时将更为显著。
为了对时域和频域滤波方法在不同数据条件下的性能进行定量分析,本文通过实验对2种方法的性能进行了验证。输入仿真数据长度为L为1 024点,滤波器系数序列点数M分别选择4,8,16,32,64,128,256,512,1 024。如此参数设置将确保仿真过程能够涵盖从M≪L到M≈L的整个范围,从而对2种算法的性能进行全面的分析。
仿真结果如图4所示,设N为运算量,M为滤波器系数个数,L为输入数据总长度。图中蓝色曲线表示时域卷积算法在不同滤波器系数M条件下运算量N随着输入数据总点数L的变化关系。绿色曲线表示频域卷积算法在不同M条件下N随着L的变化关系。图中ConvM和fftM分别表示滤波器系数为M时,时域卷积和频域滤波算法的运算量。
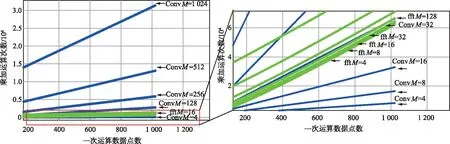
图4 时域卷积和频域卷积性能对比Fig.4 Performance comparison between time-domain convolution and frequency-domain convolution
从仿真结果可知:
① 随着滤波器阶数的增加,时域滤波方法的运算量随着处理数据点数的增加而迅速增大,与之相反,频域滤波方法在M值增加的过程中运算量并未出现剧烈变化。由此可知,在滤波器阶数较大的条件下,频域滤波算法具有较为明显的优势,而且这种优势随着M值的增加而更加明显,这与上文分析一致。
② 在滤波器阶数与数据长度相当时,频域卷积算法得优势最为明显。
③ 在M值与L值相比明显较小时,频域滤波方法的不足随着M值的减小而越发显著。在本文仿真条件下,当M值等于或小于16时,频域滤波方法在不同数据长度时的运算量和运算量增加速率均明显高于时域算法。
④ 当L值在1 024量级,M=32时,时域和频域2种卷积方法的计算量相当,且频域算法计算量增加速率更快。因此,在一次处理的输入数据较大而M不大于32时,时域算法的运算量将低于频域算法。
综合以上仿真结果分析,在长序列实时滤波运算中可得出如下结论:
① FIR滤波器阶数是影响卷积运算效率的主要因素,数据分段方法在一定条件下可以影响运算效率;
② 更高的滤波器阶数只有与之相当的数据长度时才能体现频域滤波的高效率优势,即当滤波器阶数较高时,数据段的长度最佳选择是与滤波器阶数相当;
③ 当滤波器阶数较小,小于或等于16时,无论分段长度多长,时域滤波效率均优于频域滤波效率。且在此条件下,为了减少分段处理时额外的数据拷贝消耗,更长的数据分段长度将更有利于滤波运算效率的提升。
在信道化运算过程中,各路滤波器为原型滤波器多相分解之后的序列,其长度将是M/D,其中D为多相分支的路数。在宽带数据处理中,为了最大限度降低信号速率,一般会选择较大的D,这将导致每一路分支滤波器阶数的降低。若原型滤波器长度为256,分路数D为16,则每一路分支滤波器长度即为16,在此条件下选择时域滤波算法将是最优选择,而每次处理的信号长度尽可能大将有助于提升数据处理效率。
3 实验验证
基带转换器是VLBI系统数字信号采集和处理的核心装备,其主要功能是为后端处理系统提供多通道的基带信号。由于干涉测量系统需要利用带宽综合技术对大带宽内的多个子带进行处理,因此要求基带转换器能够对宽带信号进行信道化处理,为后端处理系统输出所需的子带信号。多相信道化算法由于其高效优势在基带转换器的实现过程中得到了广泛应用,目前国际主流基带转换器均采用该算法进行宽带信号的实时处理。
为了验证以上分析结果的正确性,按照式(8)的分析结果,设计了基于GPU的VLBI多相信道化器。设每个分支滤波模块输入信号x(n)长度为L,对应的FIR分支滤波器系数序列h(n)长度为M,则基于CUDA的分支滤波算法流程如图5所示。
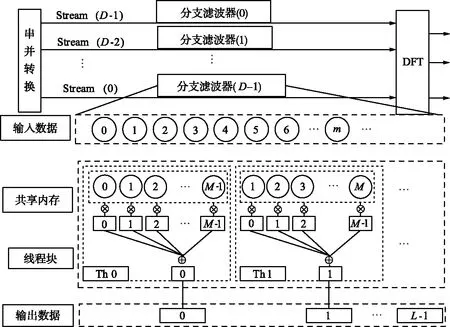
图5 分支滤波算法流程Fig.5 Block diagram of branch filtering algorithm flow
图中分支滤波模块是整个信道化模块中运算量最大的部分,每一个分支滤波器是一个独立的滤波运算单元,完成输入数据和滤波器系数的卷积运算。在多项滤波实现中,各通道输入数据和滤波器系数均已经通过多相分解实现了并行化,将各通道数据与运算流程解耦合,使得各通道数据在处理过程中相互独立。而在各通道内部,输入数据与分支滤波器通过卷积运算实现滤波操作。
由图5可以看出,输入数据被分成并行的D路,原型滤波器也做相应的多相分解,使得分支路数也为D,然后根据分支路数启动D路并行的CUDA stream。每一路数据的运算过程发生在各自的CUDA stream内,这种设计一方面充分利用了各路数据的并行性,使得各路数据处理流程在stream之间完全独立,消除了因串行等待造成的时间延迟;另一方面采用这种方法有效合并了各路数据的内存访问,解决了因内存读取不连续造成的效率降低下的问题。
由式(9)可知,在每一个CUDA stream内,实际上进行的是M点滤波器系数和L点输入数据的线性卷积运算,而对于一个输出点而言,卷积运算本质上是2个M点长度序列的逐点对应乘加。在图5所示的算法流程中,每个线程负责完成M次乘加运算并最终实现一个卷积结果的输出,所有L个线程并行启动即可完成所有输出点的运算。为了降低因运算过程中对滤波器系数反复读取造成的运算效率损失,利用线程块的共享内存存储参与运算的数据和系数。
本文VLBI基带转换器基于CUDA10.2和VS2015开发,GPU采用NVIDIA Tesla V100,信道化软硬件开发设计采用图2、图3所示多相信道化结构。输入数据在信道化入口即按通道数进行串并转换,划分为均匀的多路,然后按照通道数启动CUDA stream对每一之路数据异步并行处理。在时域卷积模式下每一个流内按照图5所示流程进行分支滤波操作,每一个流内数据处理顺序进行,各流之间数据传输和核函数的执行异步并发。在各流完成各自操作后,对各通道数据按通道数进行D点FFT,得到并行的多路基带数据输出。输出数据按要求将宽带信号均匀划分为D路。
输入数据采样率为1 024 Ms/s,信道化输出16路复信号,每一路带宽64 MHz。取0.156 25 s原始数据进行测试,即总共数据点数为1 677 216。多相滤波原型滤波器阶数255,则每路分支滤波器系数点数为16。分别按照每段数据长度1 024,4 096,65 536,262 144点对原始数据进行分段处理。分别统计每种分段长度条件下时域卷积算法和频域滤波算法条件下信道化所用时长,结果如图6所示。

图6 时域卷积和频域卷积性能对比Fig.6 Performance comparison of time domain convolution and frequency domain convolution
由图6可以看出,当滤波器阶数为15时,各种数据分段长度下,时域滤波性能均优于频域滤波性能,且随着数据分段长度的增加,2种滤波方法性能均明显增强,这与本文的预测完全一致。但是,受GPU片上资源限制,单次处理的数据长度不可能无限制增加,在数据长度超过65 536点时,算法性能增加速度变慢甚至出现下降。因此,在本文所示信道化运算条件下,以单通道每次处理65 536点数据为最佳设置。另外,从图6放大部分可看出,2种算法中每一段数据的处理耗时均随着处理数据长度的增加而近似线性增加,且频域算法的耗时增加速率明显高于时域算法,这与本文预测一致。
4 结束语
以干涉测量多相信道化基带转换器为应用背景,以基于GPU的通用计算平台为应用目标,提出一种基于CUDA的多相信道化实现方法,为了提高FIR滤波环节的运算效率,针对信道化算法中运算量最大的分支滤波模块,利用重叠保留法设计了基于CUDA的频域滤波算法和时域滤波算法。然后,利用仿真平台对2种算法的运算复杂度和适用条件进行了分析,结果显示:
① 时域滤波方法简单高效,但受卷积运算复杂度影响,单次运算量大,在滤波器阶数较低(≤16)且数据速率较高时适用;
② 频域滤波方法流程复杂,但FFT算法的应用使得运算量大大降低,适用于滤波器阶数较大(≥32)的场合。
利用以上分析结果设计了基于GPU的16通道多相信道化算法实现结构,并对该结构进行了测试,结果显示在各分支滤波器系数长度为16条件下,随着处理数据点数的增加,采用多通道并行时域卷积算法能够达到更高的运算效率,与分析结果一致。未来,该分析结果有望为干涉测量系带转换器的高效实现提供有效的技术支持。
