“都”的梯级隐含和复合命题
2021-04-09刘经安李可胜
刘经安,李可胜
(1.安庆师范大学 外国语学院,安徽 安庆 246011;2.合肥师范学院 外国语学院,安徽 合肥 230061)
一、引言
总体上看,“都”可以分为两类,一类是表示全称量化,大致相当于通常所说的表示总括的“都1”(1)“都1”以及下文中的“都2”和“都3”出自吕叔湘主编《现代汉语八百词》(增订本)。北京:商务印书馆,2001年。。下文将这类“都”简称为量化“都”,如下面(1)中各例。量化“都”字句均可以写成“都(p,q)”的形式,其中的p和q分别指称的两个集合,而“都”表示这两个集合之间的子集关系。如(1)中的句子都可以写成全称量化式,其中的上标C表示由语境确定的指称外延。
(1)a.大伙儿都同意。
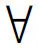
b.给谁都可以。
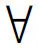
c.他都买的呢子衣服。
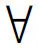
另一类“都”表示梯级隐含(scalar implicature),下文简称梯级“都”。这类“都”涵盖了表示“甚至”的“都2”和表示“已经”的“都3”。前者如(2a),后者如(2b)。
(2)a.你都搬不动。
b.都十二点了(,你还不睡)。
梯级“都”字句均可以写成“都(φ)”的形式,其中的φ是“都”字句去掉“都”后所表示的命题。所谓的梯级隐含是指,若“都(φ)”为真,则隐含一个φ的对比命题集ALT满足:依据为真的可能性,ALT中的命题形成偏序关系,且φ是ALT中最不可能成真的命题。例如,(2a)的真值条件是:“你搬不动”为真,且还存在一个形如“x搬不动”的命题集满足:若x≠“你”,则任意“x搬不动”为真的可能性都比“你搬不动”更高。正是因为这种梯级隐含的存在,梯级“都”字句可以表达说话者主观上的“出乎意料”语气。
由于梯级“都”隐含着一个ALT,因此蒋严提出梯级“都”的核心语义仍然是全称量化,其量化域是ALT[1]。这种观点得到了众多学者的支持,并以此为基础,试图为所有的“都”提出一个统一的语义解释。如潘海华等采用三分结构分析法分析所有的“都”字句[2],还有学者将“都”统一解释为最大化算子(a maximality operator)或特殊的穷尽算子(a special exhaustifier)[3][4]。
但是一个不可忽视的现象是:梯级隐含是一个语用概念,因而与说话者的意图密切相关。这种意图通常是通过与“都”字小句的关联小句表示出来的。下文分别用“都”字命题和关联命题表示“都”字小句和关联小句所表示的命题。这些关联命题可以是直接说出来的,也可以通过语境推导出来。当前的研究大多只针对“都”字命题,而不考虑包含了关联命题的复合命题,因此在解释“都”的梯级隐含时,往往会陷入一些困境中。
二、梯级隐含与对简单命题的全称量化
在现有文献中,对“都”的梯级语义分析大多数都采用类似于对even的分析方法,即依据句子的焦点给出存在隐含和梯级隐含。如Rooth以及Partee等学者认为在even的语义中存在两种隐含:存在隐含和梯级隐含[5][6]。以(3a)为例。
(3)a.Sara read even ULYSSES(Sara甚至读过《尤利西斯》)
b.存在隐含:至少存在一个命题p满足p的形式是“Sara读过x”(x不是《尤利西斯》)且p为真。
c.梯级隐含:对于任意一个命题p,若p的形式是“Sara读过x”(x不是《尤利西斯》),则p的可能性要超过“Sara读过《尤利西斯》”。
用a代表《尤利西斯》,(3)中的x是与“《尤利西斯》”构成对比关系的对比项,x的取值范围就是对比项集,记做ALT(a)。even的使用表明:《尤利西斯》是ALT(a)中最不可能被Sara读过的书。
类似的方法也被用于“都”的分析中。但是因为“都”本身具有全称量化的功能,因此很自然地将“都”的隐含意义归结为一种全称量化式。其基本思路为:存在一个对比项集ALT(a),对于任意命题p和任意x∈ ALT(a),都有px/a的可能性都要超过p(pa/x指用x替代a之后的p)。这样(3)中的存在隐含和梯级隐含就被合并表述为:隐含着一个可以被全称量化的ALT。因此,本文将这两种隐含统称为梯级隐含。
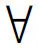
这样的做法本身并没有问题,但是有两点值得注意:一是“都”的梯级隐含不仅涉及到简单命题,还有可能是由“都”字命题和关联命题构成的复合命题。二是“都”的梯级隐含实质是表示一种主观化的情态语气,这就决定了隐含是一种可能性,而非必然性。
“都”的梯级隐含本身属于语用概念,因此“都”字句的隐含不仅仅是由“都”字小句决定的,其关联小句对梯级隐含也起到非常重要的制约作用。例如,(2b)的梯级隐含不仅仅与“都”字小句“都十二点了”有关,而且与关联小句“该睡觉了”有关。这一点下一节将具体讨论。但是这种由“都”字小句及其关联小句表示的复合命题,并没有引起学界的足够重视。一些学者试图为所有的“都”给出统一的语义刻画,往往忽视了复合命题的梯级隐含。
例如,潘海华等尝试采用三分结构分析法分析“都”的梯级语义,目标是不借助语用推理,仅通过若干映射规则,就能从“都”字的句法结构中直接推导出三分结构,即一个句子被分析成“算子(限定部分,核心部分)”(即Operator(Restrictor,Nuclear Scope))[2]。如(4)~(5)所示:
(4)a.这些书他都看过了。
b.DOU[x∈[这些书]][他看过了x]
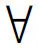
(5)a.他周末都在工作。
b.Dou[t∈ ALT(周末)][他t在工作]
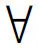
按照三分结构分析法,“都”对应全称量化算子DOU。(4a)中的“这些书”构成的集合是DOU的限定部分,而“他看过的书”构成的集合是DOU的核心部分。(4b)表明(4a)的量化结构是[这些书]⊆ {x|他看过了x}。类似地,(5a)中的“都”虽然触发梯级隐含,但也可以看成是算子DOU,只不过构成限定部分的集合不是名词词组的指称,而是ALT(电脑),即由句子的焦点“周末”的对比项构成的集合,假设是{周一,周二…,}。按照(5b)的方式,(5a)表示ALT(周末)⊆ {t|他t在工作},即如果他周末在工作,那么正常的工作日他也必然在工作。
在一定范围内,这种三分分析法可以刻画出“都”的某些梯级隐含。但是这种分析法把“都”的梯级隐含局限在简单命题上,即没有考虑关联命题,这直接会导致两个问题:一是把可能性的梯级隐含变成了必然性的蕴含;二是如果仅仅关注“都”字命题及其焦点,有一些“都”的梯级隐含就不容易得到满意的刻画。
蒋静忠和潘海华最近发表的论文中已经意识到第一个问题。虽然焦点的候选项集合中存在梯级序列,但是这种序列只是一种可能性(likelihood)。也就是说,若p为真的可能性比q低,则即便p为真,也不意味着为真可能性更高的q也为真。但是如果按照(5b)的方式给出全称量化式,则无疑将这种可能性转变成了必然性。以下面的(6a)为例,句子的焦点“周末”引出的对比项集是(6c)。若(6a)为真,则必然存在一些工作日x满足:小李x上班,但是这并不意味着小李在所有的工作日都在上班。
(6)a.他周末都在上班。
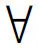
c.{星期一,星期二,...,星期五}
假定,“他”在周一至周三时休息,但是周四上班后工作非常忙,导致在周六时不得不加班,那么在此语境下,(6a)仍然是合适的,但是(6b)并不为真。事实上,(6a)中的“都”只是表明在说话者心目中,如果“他周六上班”为真,则“他x上班”(x是工作日)更有可能为真,但是(6b)的全称量化式却将隐含变成了蕴含。
关于第二个问题。如果仅依据“都”字句及其焦点进行分析,有些“都”字句的梯级隐含是很难用ALT的方式进行刻画的。如果为了强行贯彻三分结构分析法,会导致一些悖论的出现。
例如,在下文(7a)中,焦点是“黑”,与“(天)黑”构成对比关系的ALT是{(天)黑、(天)暗、(天)亮}。按照(5)的处理方式,就得到了(7b)和(7c),即“对于每一个P来说,如果‘(现在)天P了’为真,那么P就等于‘黑’”[7]。
(7)a.天都黑了。
b.DOU[(现在)天P了] [P = 黑]
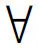
但是这种分析存在两难问题。如果要满足“都”的存在隐含,则必然存在一个形如“(现在)天P了”满足:P ≠“黑”且P为真。这必然意味着ALT(黑)是一个多元集。假设ALT(黑)= {亮了,暗了,黑了}。按照(7b)的分析,只要P是ALT(黑)中的任意一个状态,都蕴含着P等于“黑了”,即无论P取什么样的值(假设是“亮着”),P都等于“黑了”。换言之,如果“天亮着”,那么“天黑了”,这显然是矛盾的。
如果要消除矛盾,(7c)的定义域就必须是独元集,也就是ALT(黑)中只包含一种选项,即ALT(黑)= {黑了}。这样如果P∈ALT(黑),则必然有P =“黑了”。但这样的话,等于直接否定了“都”的存在隐含,因为没有一个形如“(现在)天P了”且P ≠“黑”的命题为真。
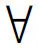
强行采用三分结构分析法的另一个结果是:虽然有些“都”字句可以通过ALT给出全称量化式,但是不能真正捕捉到梯级隐含对话语交际的贡献。以“都十二点了”为例,潘海华认为可以按照“连十二点半都过了”进行分析[2]。
(8)a.都十二点半了 ≈ 连十二点半都过了
b.Dou[t∈ ALT(十二点半)][t过了]
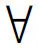
姑且不论“连十二点都过了”是否与“都十二点了”完全一致,从(8c)中也看不出“都”的语义贡献。因为把(8a)中的“都”去掉,直接说“十二点半了”,(8c)仍然成立。显然,这样的语义很难真正体现说话者的意图。
除此之外,将ALT限定为句子焦点的对比项集,也会带来一定的问题。例如,“局长都到医院看望小张了”可以有两种理解。一是“很多人都来看望小张,连最不可能来的局长都来了”。第二种理解是“小张在单位很受重视,所以才有局长这样重要的人物来看望”或者“局长对小张的非常关心,所以亲自来看望”。
如果是第一种理解,则句子的焦点是“局长”,而ALT中的对比项都与“局长”构成对比关系。同时这也意味着除了局长之外,应该还有其他人来看望小张。否则“局长都到医院看望小张了”就是不合适的。但是如果是第二种理解,那么即便除了局长之外,没有其他任何人来看望小张,这句话也是合适的。在这种情况下,该句本身就没有焦点,但是仍然存在一个ALT,只不过ALT中的对比项不是形如“x来医院看望小张了”,而是其他类型的命题。例如,如果说话者意图是表示“小张在单位很受重视”,那么可能包括在ALT中的命题有“小张入职后很快得到了提拔,单位给了小张特殊待遇”等等。如果说话者的意图是表达“局长关心小张”,则ALT中可能包括“局长托人问候小张,局长打电话询问小张的病情”等,这些命题为真时所体现的“局长”对“小张”的关心程度显然不如“亲自到医院看望小张”。
综上所述,对“都”的梯级隐含刻画,一不能改变隐含的可能性,二不能仅仅局限于“都”字命题本身,还需考虑关联命题。
三、复合命题的梯级隐含语义表征
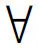
但是向明的处理还是存在一些问题,即没有考虑关联命题对梯级隐含的贡献。先看(9a)和(9b)两个例句。虽然都有“都十二点了”,且焦点都是“十二点”。如果按照向明的处理方式,则(9a)和(9b)中“都十二点了”有着相同的梯级隐含,即(9c)。
(9)a.啊!都十二点了!时间怎么过的这么快。
b.都十二点了!该下课了。
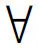
但是(9a)和(9b)中的梯级隐含并不相同。(9a)表明说话者原本预料现在的时间应该早于12:00(假设他预料现在最多是11:40),当他发觉现在是12:00时,就会惊讶地说出(9a)。显然“现在是12:00”比“现在是11:40”更加出乎说话者的意料,所以(9c)刻画出了(9a)的梯级隐含。
但是(9c)并不能刻画出(9b)的梯级隐含。在(9b)的语境中,学生希望老师快点下课。这意味着,在该语境中,说话者非常清楚现在是十二点,而且因为一直盼望着下课,所以对十二点之前的时间流逝也都非常清楚,不存在意料之外的情况。事实上,在(9b)的语境中,真正出乎意料的不是“都”字命题“现在是十二点了”,而是关联命题“还没有下课”。据此可见,如果仅仅考虑“都十二点了”,是无法给出(9b)的梯级隐含的。只有将(9c)的后半部改成unexpected(在12:00时,没有下课)> unexpected(在t时,没有下课)(2)这里t的取值范围是正常的下课时间到12:00之间的时间。,(9c)才能刻画出(9b)的梯级隐含。所以要想充分刻画出“都”的梯级隐含,必须将关联命题考虑在内。
在当前的文献中,大多数都是将“都(φ(α))”中的φ看成是一个简单命题,也就是“都”字小句所表示的命题。但是实际上,φ完全有可能是一个复合命题,即不仅仅包括“都”字小句表示的命题,还包括与其关联小句所表示的命题。在这种情况下,“都”的梯级隐含就应该分析成(10a)。
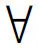
这里的DOU是与“都”对应的梯级隐含算子,“φ都”表示φ是“都”字命题(即“都”字小句所表示的命题),ψ表示制约“都”字命题的关联命题,R(φ, ψ)表示命题ψ和φ在为真时存在的某种关系。注意,这里的ψ可以空缺。若ψ空缺,则R(φ, ψ)也就简化为 R(φ)。在这种情况下,(10a)就等同于(10b),与向明的语义表征式类似。只不过(10)中的ALT是对比命题集,而非前文的对比项集。
依据(10),“都十二点了”在(9a)和(9b)中不同的梯级隐含就可以分别被分析为:
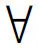
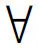
(11)中粗体并加着重号的词语表示两个命题之间的关系。例如,“为真”可以定义为:p为真当且仅当 存在某个情境s使得命题p的真值条件在s中得到满足。“……在……为真时为真”可以定义为:p在q为真时为真当且仅当 使得q为真的情境s呈现时,p在s中也为真。依据同样的分析,虽然(12)中的两个句子都有“小李都生孩子了”,但因为上下文不同,两个句子有着不同的梯级隐含。
12.a.小李都生孩子了,你啥时候生啊?
b.小李都生孩子了,身材还那么好!
(12a)表明,在说话者心目中,与相关的女孩相比,“小李”生孩子的可能性是比较低的。因此让说话者感到意外的是“都”字命题本身,即“小李生孩子”。这也意味着,对任意的一个p∈ ALT(小李生孩子了),都有unexpected(小李生孩子了)> unexpected(p),其中的p是形如“x生孩子了”的命题。但是在(12b)中,让在说话者感到意外的并不是“都”字命题,而是关联命题“身材还是那么好”。所以(12)的梯级隐含应该是(13)。
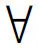
下面的例句又有所不同,该句子存在(14b)和(14c)两种歧义。
(14)a.小李吃饭时都在看书。
(10a)所表示的命题是由两个简单命题构成的,即“小李吃饭”和“小李看书”。(10b)意味着“小李在吃饭时看书”比“小李在其他场合下看书”更超出说话者的预期,在这种解读下,ALT中的对比项都与“吃饭”构成对比关系,如“上课,休息,睡觉前”等。但是(10c)意味着“小李在吃饭时看书”比“小李在吃饭时做其他事情”更超出说话者的预期,在这种解读下,ALT中的对比项都与“看书”构成对比关系,如“聊天,看电视”等。
四、梯级隐含的情态功能和ALT的虚拟性
虽然本文赞同蒋严和潘海华等学者们的主张,即梯级“都”的基础是全称量化,但是在现代汉语中,梯级“都”的主要功能是借助梯级隐含,表达某种主观化的情态语气。在这种情况下,全称量化的功能已经弱化。例如,张谊生提出:“在‘连NP都VP’这样的格式中,‘都’在表语气情态的同时还带有量化痕迹——尽管在不同的语境中这种量化痕迹的强弱程度不等。然而,一旦‘连’字不再出现,整个格式原有的强调焦点的情态功能全被‘都’吸收(absorb)了”[9]。
梯级“都”具有情态功能,具体表现在ALT的虚拟性上。这种虚拟性一方面体现在ALT中所包含的内容并不是说话者关注的内容,因此在很多语境中,并不能说清楚ALT中到底包含了什么样的内容。另一方面,对ALT的全称量化并不需要在参照世界中进行印证。即便在参照世界中,ALT中的内容不存在,也不影响梯级“都”的情态功能。
仍以“都十二点了,该下课了”为例。正常情况下,当学生对老师说出这句话时,表明在说话者看来,在“十二点”之前还存在一个时间点t满足:在t时,就应该下课了。假设正常的下课时间是11:45,那么11:45-12:00之间的所有时刻,都满足“该下课了”的性质。换言之,所有形如“(现在是)t了”的命题,若满足t的取值范围是从11:45到12:00之间的时刻,则这样的命题就构成了“(现在是)十二点了”的对比命题。如下图所示,ALT包括了时轴上11:45到12:00之间的所有黑点。此种情况下,ALT在参照空间是一个多元集,这是说话者对梯级“都”的正常使用。
但是还有一种情况,假如正常下课时间就是12:00,那么满足“该下课了”的时间只有图1中的“12:00”。此时的ALT就变成了独元集,这意味着没有存在隐含和梯级隐含。理论上,此情况就不应该产生梯级隐含。但实际情况并非如此,“都”仍然产生了梯级隐含,并以另一种方式为话语交际做出贡献,即学生使用梯级“都”向老师表明他很不耐烦地在等待着下课。

图1
这种信息的表达渠道大致是:当说出“都十二点了,该下课了”时候,按照梯级“都”的语义设定,除了在“十二点”这个时间之外,还应该至少一个比12:00更早的时间t满足:“该下课了”在t时为真。既然事实上,12:00是该语境中唯一该下课的时刻,说话者就违反了“都”的语义设定。从语用学的角度看,说话者违反了格赖斯合作原则中质的准则(the Maxim of Quality)。同时按照交际关联原则,老师会进一步推断,在说话者心目中,在正常的下课时间12:00之前还应该有一个该下课的时间。这也就意味着说话者认为老师应该在正常的下课时刻之前下课,据此可以推断出老师的课不受学生欢迎。所以若正常下课时间就是12:00,而学生说出“都十二点了,该下课了”,老师通常会感到生气或沮丧。
但是若正常下课时间在12:00之前,因为ALT是多元集,老师就不太可能得到类似推断,而且ALT集合越大(即说话时间和正常下课时间间隔越长),得到类似推断的可能性就越小。
另一个典型例子是“我都六十了,该退休了”。法定退休年龄是六十岁,所以在“六十岁”之前并不存在一个年龄满足“我该退休”。在这种情况下,该例的ALT也是独元集。但这句话仍然是合适的,原因在于:说话者使用了“都”,通过“都”的语义中应该包含了一个多元集ALT,说话者表达这样的意思,即按照“我”自己的考虑,“六十岁”之前,我就准备好退休了(无论是出于无奈还是一种希翼)。
综上所述,梯级“都”的主要功能是触发ALT,并通过ALT产生梯级隐含,从而表达某种主观化的情态语气。
五、结语
本质上,梯级“都”可以看成是与even类似的一个梯级隐含算子,在其所触发的隐含语义中包含了存在隐含和梯级隐含。在“都”本身具有全称量化功能的情况下,“都”的存在隐含和梯级隐含可以合并表述为“存在一个可以通过可能性进行全称量化的对比命题集ALT”。但是“都”的全称量化不仅仅涉及到简单命题,即“都”字命题,还有可能是一种复合命题。后一种情况实际上反映了“都”的梯级隐含与说话者意图之间的关系,这也是其语用性质的反映。正是因为有后一种情况的存在,对梯级“都”的语义刻画就不能仅仅局限于“都”字小句及其焦点。
