废水处理过程的抗扰控制研究

魏伟，蔡欣宇，刘载文，左敏

（北京工商大学计算机与信息工程学院，北京100048）

引 言

随着我国经济的快速发展，工业废水、城市污水的排放日益增多[1]。然而，目前，我国工业污水存在排放不达标的问题[2]，由此造成水资源污染，进而导致人民健康得不到保障。因此，为保障人民生命健康、实现水资源的可持续利用，必须高度重视废水处理[3]。

厌氧消化废水生物处理工艺是广泛应用于农业、制药和食品工业的废水处理方案。厌氧消化过程能够产生甲烷，并从污水中去除有机污染[4]。典型的厌氧消化过程包含四条代谢途径，两条用于产酸，两条用于甲烷化。细菌在缺氧环境下，将有机物分解为二氧化碳、甲烷和水[5]。

厌氧消化废水生物处理的控制目标是降低其污染水平[6]。然而，这一复杂的动态反应具有高度非线性、参数未知的特征[5]，并且整个生化反应存在着诸多不确定因素，如：输入组分、组分浓度的变化以及不确定的动力学参数等[4,6]，这些都给废水处理过程控制带来了极大的挑战。为克服这些因素对废水处理过程控制带来的挑战，各种先进控制技术相继提出，如反馈线性化技术[7]、自适应控制[8]、滑模控制[9]等。反馈线性化技术是一种有效的非线性控制设计方案，但它需要系统的全部先验知识[10]。文献[8]提出了一种非线性自适应控制策略，通过状态观测器和线性回归参数估计器，实现对部分变量以及动力学参数的估计。然而，它依旧需要了解厌氧过程的所有输入[11]。滑模控制的优点在其鲁棒性强，但其缺点在控制信号的抖振[12]。

事实上，若将厌氧消化过程中的各种不确定因素视为影响输出污染水平的扰动，从抗扰控制的角度出发，实时估计并补偿这些不确定因素，可获得期望的控制效果[13-17]。

考虑到废水生化处理过程非常复杂，具有强非线性、时变特征，且无法确切获得其生化反应动态，本文设计一种抗扰控制方法，实时估计并补偿厌氧消化过程中的总扰动，控制输出污染水平，进而获得期望的污水处理效果。

1 厌氧废水降阶模型

厌氧消化处理过程是不同的代谢微生物相互影响、相互制约而形成的复杂生态系统[18]，其建模、控制有诸多报道[5-6,9,12]。废水生化处理过程的强非线性、时变性使其动态模型非常复杂，通常由10 个微分方程来描述[5]。从控制系统设计角度，本文采用与文献[5]相同的降阶模型

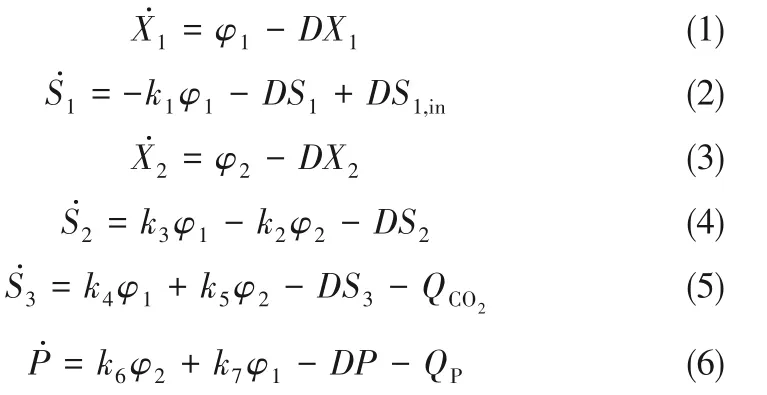
其中，φ1和φ2分别是第一次产酸反应和甲烷化反应的速率，QP=cpP 和QCO2分别表示甲烷和二氧化碳的气体流出率。cp＞0，每个反应速率都是一个增长速率，可写为φi=μiXi，i=1,2，μi是反应i 的增长速率[5,18]。μ1由Monod 定律模拟[19]，且μ1=μ01S1/(KM1+S1)；μ2由Haldane 定律模拟[19]，且μ2=μ02S2/(KM2+S2+S22/KI2)。这里μ01、μ02是最大增长速率，KM1、KM2是饱和常数，KI2是抑制常数[6,20]。

定义状态向量ζ=[X1,S1,X2,S2,S3,P]T，则模型(1)～模型(6)可写为[5]

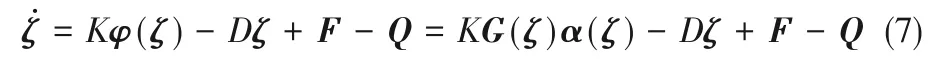
式中，流入率F=[0,DS1,in,0,0,0,0]T，气体输出率Q=[0,0,0,0,QCO2,QP]T，反应速率φ=[φ1,φ2]T，且φ(ζ)=G(ζ)α(ζ)。G(ζ)为对角矩阵，是每个反应中所涉及的组分浓度的乘积，α=[α1,α2]T是特定反应速率向量，αi=μi/Si,i=1,2，K是产率系数矩阵。矩阵K、G具有以下结构[5]

对于动力学模型(7)描述的厌氧生物过程，令输出污染水平为受控量，并定义其为[6]

其中ω1、ω2是已知的转换系数，选择稀释率D作为控制信号，即u=D。

由系统输出(9)和模型(1)～模型(6)，可得输入输出过程模型[6]

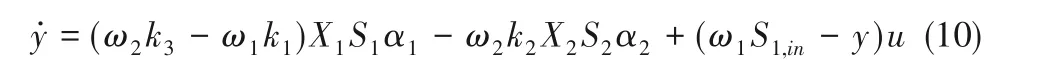
该系统的控制目标是使输出y 保持在一个期望的低水平y*∈R+。反应涉及的变量及其名称见符号说明，生物过程参数见表1。

2 抗扰控制设计

2.1 控制问题描述

由系统(10)知，输出污染水平(y)受产酸菌浓度X1、产乙烷菌浓度X2、葡萄糖浓度S1、乙酸浓度S2、进水底物浓度S1,in以及反应速率等诸多因素影响。在废水处理过程中，这些量随时间变化，且各变量间相互耦合。同时，厌氧消化处理过程存在大量不确定因素，如组分变化、进水底物浓度变化以及动力学参数变化等。这些厌氧消化处理过程的不确定（扰动）因素给废水处理过程控制(使输出污染水平y保持在较低值)带来了极大的挑战。因此，对模型信息依赖性小、能够克服废水生化处理过程中各种不确定因素影响的控制方法，有望在废水处理过程中获得期望的控制效果。

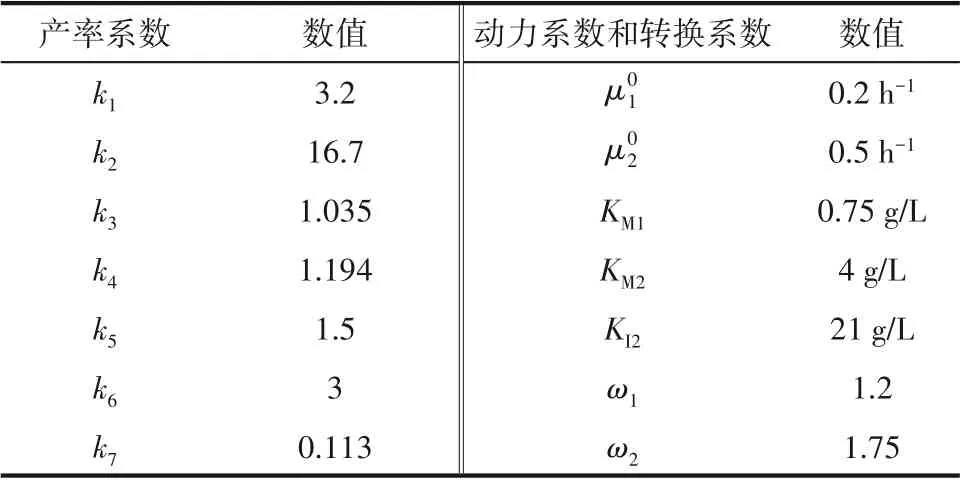
表1 生物过程参数Table 1 Biological process parameters

厌氧消化处理输入输出过程模型(10)可改写为

其中，d 为系统的总扰动，且d =(ω2k3-ω1k1)X1S1α1- ω2k2X2S2α2+(ω1S1,in- y - 1)u。

基于厌氧消化处理过程的特点以及输出污染水平的控制要求，本文采用抗扰控制[21]。其控制思想与自抗扰控制思想相似，即主动估计并补偿系统中非线性动态、模型不确定性以及外部扰动等综合因素（总扰动）。

2.2 抗扰控制器

对于单变量非线性系统[21]

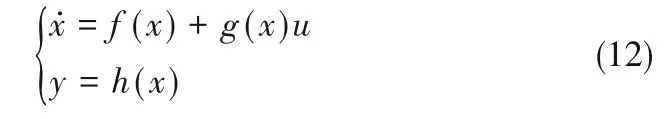
设系统的相对阶r 已知，其输出y 及y(i)[1≤i≤(r-1)] 可 测，那 么，存 在 同 胚 变 换zi= φi(x) =Li-1fh(x),i = 1,2,…,r; wi= φi(x),i = 1,2,…,n - r，将系统(12)化为如下标准型

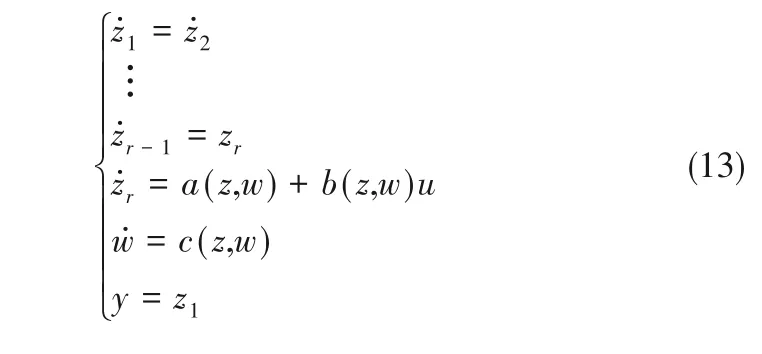
对于系统(13)，将其中未知或不确定的量定义为系统的扩张状态d(z,w,u)=a(z,w)+[b(z,w) -1]u。将扩张状态代入标准型，得到包含扩张状态的形式z˙r= d(z,w,u) + u。为估计并补偿包含系统内部不确定性以及外部扰动的总扰动d(z,w,u)，抗扰控制(disturbance rejection control,DRC)可设计为[21]

对于本文考虑的污水处理系统(10)，设计如下抗扰控制器

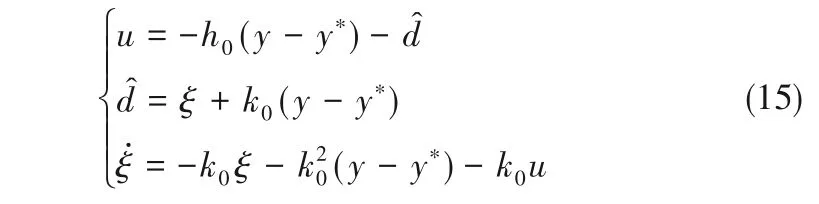
式中，y 是系统输出，y*是期望的系统输出，是总扰动(ω2k3-ω1k1)X1S1α1-ω2k2X2S2α2+(ω1S1,in-y-1)u 的估计值，ξ 是一个中间变量，h0、k0是需要调节的控制器参数。

输出污染物的抗扰控制结构如图1所示。

图1 厌氧废水处理过程输出污染物抗扰控制Fig.1 Disturbance rejection control of the output pollutions in an anaerobic wastewater treatment process

2.3 稳定性分析

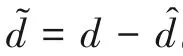
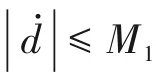
证明：

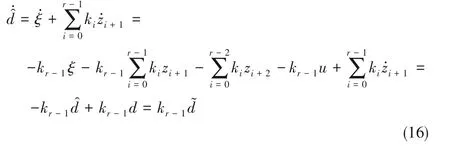
其中，kr-1为观测器增益且kr-1＞0，有

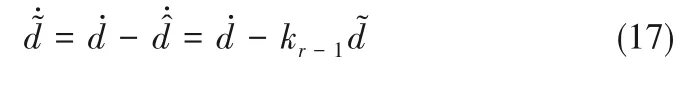
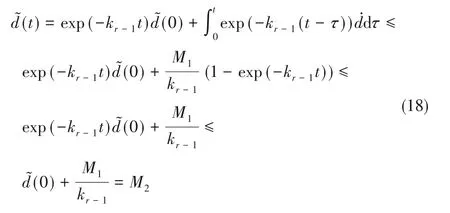
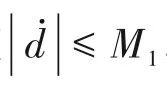
证明：对于有界输入y*，利用观测器的总扰动估计以及可测的y(i)[1≤i≤(r-1)]，作如下反馈控制

记 y*1= y*,y*2= y˙*,…,y*r+1= y*(r),y = z1,z˙1= z2,…,z˙r= zr+1跟随偏差ɛi= y*i- zi。

将控制律(19)代入z˙r= d(z,w,u) + u，有

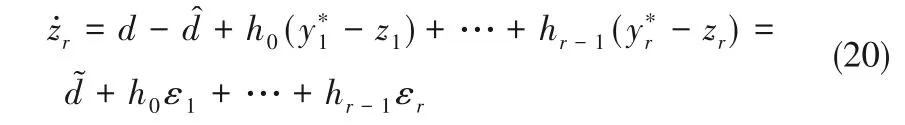
可得

即

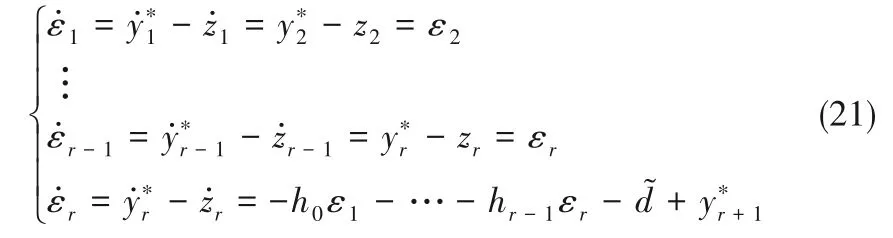
选取hi(i=0,…,r-1)使A1有r 个不同的特征值λ1,…,λr且λ1＜…＜λr。那么，存在可逆阵T，使得A1= Tdiag{-λ1,…,- λr}T-1，则

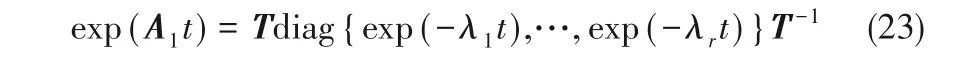
且有

同样地

那么

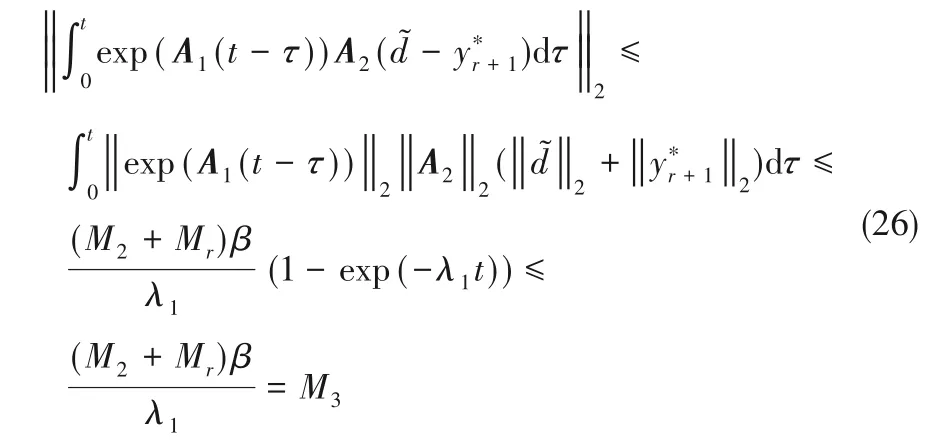
也就是说，跟随偏差有界。那么，对于有界输入y*，其输出也必然有界。因此，闭环系统是有界输入有界输出稳定的。

2.4 扰动观测能力分析

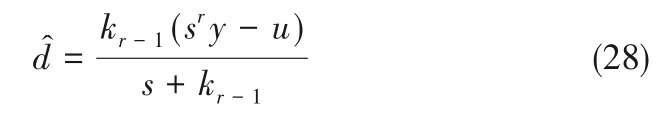
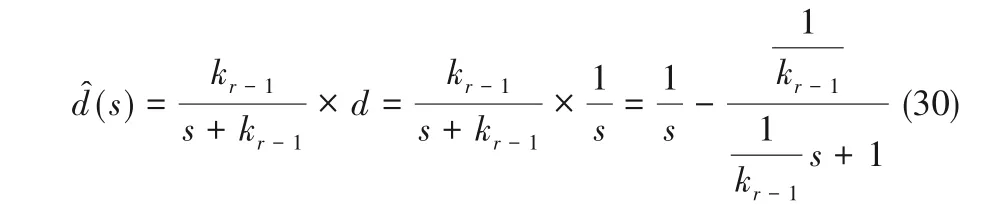
于是

在概念网络中，依据概念不同的特征，可以形成不同的概念聚类。基于语义的相似性形成的概念聚类和基于主题的相关性形成的概念聚类，与类比推理的研究密切相关。

于是

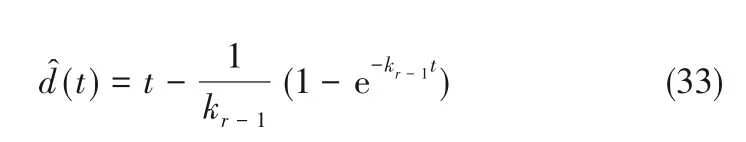
可见，观测器的性能与kr-1有关。由式(31)、式(33)知，增大kr-1可加快总扰动的估计速度；同时，由式(34)知，增大kr-1可减小观测器估计斜坡总扰动的稳态误差。

由上述分析可知，对于1阶系统，若总扰动为单位阶跃信号，观测器可实现对总扰动的无差估计；若总扰动为单位斜坡信号时，观测器的性能仅与k0有关。k0越大，观测器估计总扰动的速度越快、总扰动估计的稳态误差越小。

3 数值仿真

本节以厌氧废水降阶模型(7)模拟两种情形下抗扰控制、PI 控制以及精确反馈线性化(exact feedback linearizing,EFL)控制对输出污染水平的调控效果（控制参数见表2）。仿真中，设定输出污染水平在0.3～1.5 间变化（图2）。假定进水底物浓度S1,in可测，且

表2 EFL、PI与DRC控制参数Table 2 Control parameters of EFL，PI and DRC

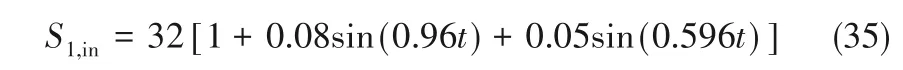
S1,in变化见图3。

PI控制律为

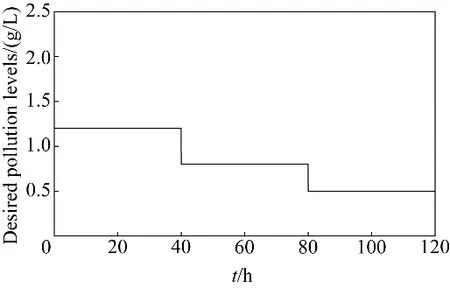
图2 设定的输出污染水平Fig.2 Set values of the pollution levels

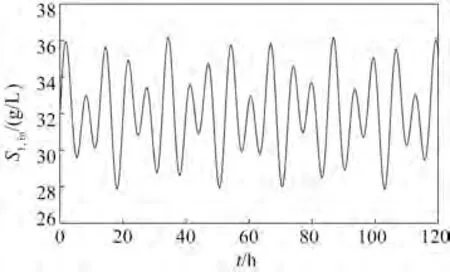
图3 进水底物浓度Fig.3 Influent substrate concentrations

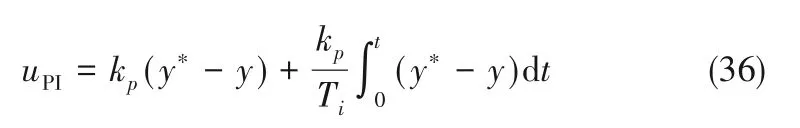
其中，y*- y为控制偏差，kp、Ti为控制参数。

精确反馈线性化控制律为

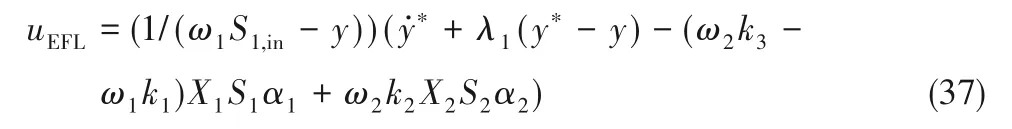
其中λ1为控制参数。

参照式(15)，DRC控制律可设计为

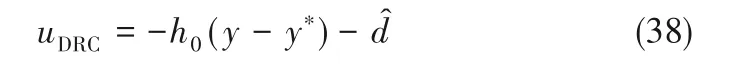
其 中，h0为DRC 的 控 制 参 数，为 总 扰 动 的估计。

采用时间乘以误差绝对值积分(integral of timemultiplied absolute-value of error,ITAE)、误差平方积分(integral of squared error, ISE)定量比较不同控制策略的调控效果。

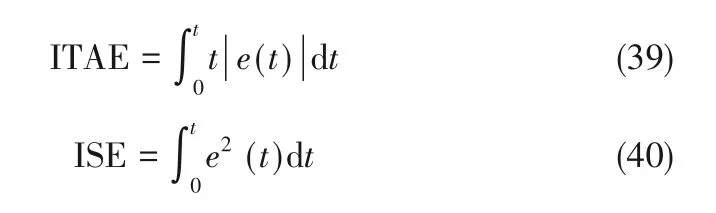
考虑理想情况以及加入扰动两种情形。两种情形的初始条件一致，取值为[19]

（1）理想情况

理想情况, 即过程（10）的特定反应速率向量α =[α1,α2]T完全已知，且所有变量都可测。三种控制方法的输出污染水平和控制信号如图4所示。

图4 理想情况下污染水平控制效果及控制信号Fig.4 Pollution levels and control signals in an ideal case

可见，三种控制方法均可控制输出污染水平跟随设定值变化。DRC 控制信号的变化与另外两种控制信号波动的趋势相似，且在设定值跳变时，DRC的控制信号也随之变化。同时，从系统响应的局部放大图可以看出，在设定值发生改变时，DRC 的响应速度更快，其控制效果优于PI 和EFL。三种控制的性能指标如表3 所示。与EFL 对比，DRC 的ITAE指标降低了79.68%，ISE 指标减小了94.87%；与PI对比，DRC 的ITAE 指标减少了74.89%，ISE 指标减少了65.83%.

表3 理想情况下的ITAE与IAE指标Table 3 ITAE and IAE values in an ideal case

（2）加入扰动

考虑输入端扰动以及反应i 的增长速率发生变化两种情形。三种控制方法对应的输出污染水平和控制信号如图5所示。这里输入端扰动设为正弦扰动[0.2sin(t)]；同时，假设最大增长速率、非定值，而是两个时变参数[5]，记为μ01(t)、μ02(t)，且

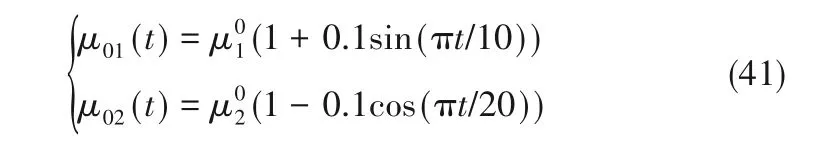
由图5(a)可见，存在扰动时，DRC 的响应与设定值的偏差最小。这表明，扰动存在时，精确反馈线性化控制由于对模型信息依赖大，没有实时估计、补偿扰动的能力，输出响应已明显变差。PI 与DRC则因具有较好的适应性，仍可较好地跟随设定。同时，由图5(b)可知，DRC 以相似的控制信号获得了比PI 更好的设定值跟随效果。三种控制的性能指标如表4 所示。与EFL 相比，DRC 的ITAE 指标减少了99.74%，ISE 指标降低了99.93%；与PI 相比，DRC 的ITAE指标降低了74.89%，ISE指标减少了93.25%。

上述数值仿真结果表明，理想情况下，稳态时，抗扰控制与精确反馈线性化控制有比较接近的控制效果，且二者均优于PI 控制。同时，在设定值跳变时刻，抗扰控制动作更快，使系统响应能够及时跟随设定。存在扰动时，抗扰控制明显优于精确反馈线性化控制以及PI 控制，这表明面对不确定性因素时，抗扰控制能够较好地估计并补偿各种扰动因素对系统输出的影响，以保证控制效果。

图5 加入扰动时的污染水平控制效果及控制信号Fig.5 Pollution levels and control signals in presence of disturbances

表4 扰动情况下的ITAE与IAE指标Table 4 ITAE and IAE values in presence of disturbances

4 结 论

本文研究了厌氧污水处理过程输出污染水平的控制问题。采用抗扰控制，研究两种情形下污染水平的抗扰控制，并与精确反馈线性化控制及PI 控制作对比。仿真结果表明，尽管在理想情况下，稳态时，DRC 的控制精度与精确反馈线性化控制相近，但是，当扰动存在时，抗扰控制相比于精确反馈线性化控制和PI 控制，其控制效果更佳。同时，需要指出，精确反馈线性化控制是一种较为理想的控制方法，其控制律是以被控对象信息完全已知为前提的。然而，抗扰控制对被控对象的依赖更小，能够实时、有效地估计并补偿扰动，以尽可能地减小扰动对输出的影响、保证良好的控制效果。因而，抗扰控制是一种更为实用的污水处理过程控制方法。

符 号 说 明

D——稀释率，h-1

ki——产率系数

P——甲烷浓度，g/L

QCO2——二氧化碳气体流出率,m3/h

QP——甲烷气体流出率,m3/h

S1——葡萄糖浓度，g/L

S1,in——进水底物浓度,g/L

S2——乙酸浓度，g/L

S3——二氧化碳浓度，g/L

X1——产酸菌浓度，g/L

X2——产乙烷菌浓度，g/L