基于Ms-NIPLS-GPR 的化工过程性能等级评估方法

王浩东，王昕，王振雷，曹晨鑫

（1 华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海200237； 2 上海交通大学电工电子实验教学中心，上海200240）

引 言

随着时代的发展，人们对生产过程自动化程度的要求也随之提高。生产系统在使用初期一般具有良好的运行性能，但由于仪表失准、传感器故障、执行机构磨损等因素的影响会使生产系统出现生产性能下降的情况，造成产品质量下降和生产成本提高等问题。因此一个高效准确的性能评估方法对生产效率的提升和企业经济收益的提高至关重要。

1989 年，Harris[1]提出基于最小方差控制（MVC）的性能评估方法，并将其作为评估单输入单输出（SISO）系统性能下限，这一研究成果标志着性能评估研究方向的诞生。1996年，Harris等[2]把单变量最小方差基准的性能评估方法推广到多变量控制系统中。之后，学者们针对不同控制系统特性设计了符合实际工况的性能评估基准，如广义最小方差（GMV）基准[3]、线性二次型高斯（LQG）最优控制基准[4]、用户自定义基准[5]等。这些评估方法大多依赖于机理建模和先验知识，而实际过程的精确数学模型往往难以得到，限制了这些方法的实际应用。

针对以上问题学者们提出一种基于数据驱动的建模方法，该方法的原理是从过程数据中挖掘出研究需要的信息，其优点在于减少了对机理模型的依赖且过程数据容易获得。Qin 等[6-7]提出一种基于数据的协方差基准来评估多变量系统的性能。2012 年，Qin[8]总结了数据驱动在过程监测与故障诊断上的应用和未来发展方向，引起了学者们的广泛关注。

现代工业生产过程往往具有复杂多变、过程变量众多以及数据非线性等特点，从而无法进行准确的性能评估。为了解决复杂工业过程性能评估的问题，多元统计过程监控（multivariate statistic process monitoring，MSPM）方法应运而生，其中典型代表有主元分析（principal component analysis，PCA）、偏最小二乘（partial least squares，PLS）[9-12]。Liu 等[13-14]采用PCA 特征提取方法提取每个性能级的主要变化信息，以此建立性能级离线模型，根据在线数据特征匹配结果进行性能评估。但PCA 属于无监督建模方法[15]，所以缺乏标签变量的引导，该评估方法的抗干扰能力较弱。PLS 属于有监督建模方法，为使其适应数据的非线性特征，Yan 等[16]采用基于核函数PLS 模型进行仿真预测，但该方法中核函数及其参数通常由经验和反复试验确定，因此浪费大量时间和资源。曹晨鑫等[17]采用局部加权潜结构映射（LWPLS）与神经网络相结合的方法，不但改善了数据间的非线性关系而且提高了训练数据与性能等级的匹配精度，但神经网络存在需调节参数多、过拟合等问题，难以达到良好的评估效果。

因此，本文提出一种基于多数据空间非线性迭代偏最小二乘和高斯过程回归（multi-space nonlinear iterative partial least squares and Gaussian process regression，Ms-NIPLS-GPR）的化工过程性能分级评估方法。首先利用Ms-NIPLS 算法对不同稳态性能等级数据进行非线性特征提取，然后以此建立高斯过程回归离线模型。在线评估时，提取滑动时间窗内数据的特征子空间作为离线模型的输入，对模型输出应用变遗忘因子数据处理技术并结合构造的过渡性能系数来判断当前过程的性能等级和性能状态。最后，使用PCA-NN、Ms-PLS-NN、Ms-NIPLS-GPR 方法对乙烯裂解过程数据进行分析评估，验证本文性能评估方法的可行性和准确性。

1 多数据空间NIPLS-GPR方法

多数据空间是一个包含多个不同性能等级数据的集合。多数据空间NIPLS-GPR 方法适用于分析多变量间的非线性关系，其原理是利用Ms-NIPLS 来适应过程数据间的非线性关系，通过提取不同性能等级数据在数据标签引导下的特征子空间，从而剔除不能解释标签数据变化的过程变量，并在相关过程变量和数据标签之间建立非线性映射模型。

1.1 非线性迭代偏最小二乘方法

NIPLS 是一种改进PLS 内部模型的算法，弥补传统线性PLS 模型在实际应用中的不足。目前，PLS 的非线性扩展方法主要分为两类，一种是引入核函数[18-20]，将数据间的非线性关系线性化，再通过线性PLS 建模，该方法对于核参数选择要求较高。故采用改进PLS 内外模型的非线性扩展方法[21-22]。NIPLS 通过迭代方式构建PLS 模型，计算量较小，有利于在线评估。

对于单数据空间，假设过程变量X ∈Rn×m包含n 个样本，m 个过程变量，质量变量Y ∈Rn×p包含p个质量变量。NIPLS算法执行过程如下：

对X、Y 进行零均值、单位方差标准化处理，令i = 1，X1= X。

A 代表NIPLS 方法提取潜变量的个数，可由交叉验证法得到[23]。使用NIPLS 算法对(X,Y)进行非线性迭代分解，分解形式如下：

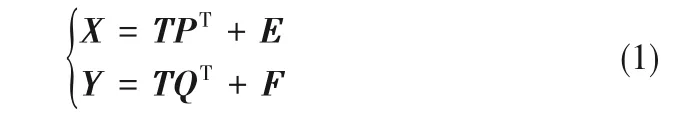
式中，T、P、E分别为输入矩阵X的得分矩阵、负载矩阵、残差矩阵，Q、F分别为输出矩阵Y的负载矩阵、残差矩阵，TPT则代表与输出矩阵Y 变化相关的特征子空间。

1.2 高斯过程回归方法

高斯过程回归是一种通过推断训练数据集中的输入向量与目标输出向量函数关系f，从而确定目标输出条件分布的机器方学习法，具有泛化能力较好、模型超参数自适应、方法易实现等优点[24-25]。对于给定训练数据集D ={(xi,yi)|i = 1,2,…,n}=(X,Y)(其中xi代表第i个样本输入，yi代表第i个样本输出),回归模型可以表示为

由式（2）～式（4）可得输出值y的先验分布为

式中，I 为单位阵，K = K(X,X) = k(xi,xj)n×n为对称的协方差矩阵，k(xi,xj)刻画了xi和xj之间的相关性。所以训练样本输出y与测试样本输入x*所对应的输出y*的联合分布为

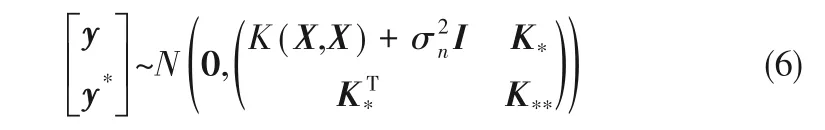
式中，K*= K(X,x*)= K(x*,X)T为训练数据集X与测试样本x*之间的协方差矩阵，K**= k(x*,x*)为测试样本x*的自协方差。

由贝叶斯原理可得输出值y*的后验概率分布为

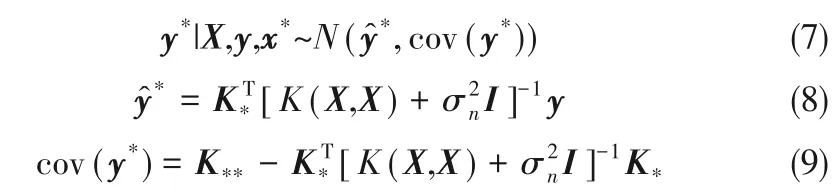
1.3 Ms-NIPLS-GPR 方法

由于不同性能等级数据集对应的特征子空间存在不可忽视的差异性，所以本文提出Ms-NIPLSGPR方法。首先利用NIPLS算法对每个性能等级数据集进行特征提取以准确区分各个性能等级的特征，然后在提取的特征子空间与数据标签间建立高斯过程回归模型。

假设有C个数据空间，那么第i个输入输出空间为Xi∈Rni×m、Yi∈Rni×p，i = 1,2,…,C，m、p 为过程变量、质量变量个数，ni为不同数据空间采样点个数。

具体的算法步骤如下。

（1）对多个数据空间使用NIPLS算法

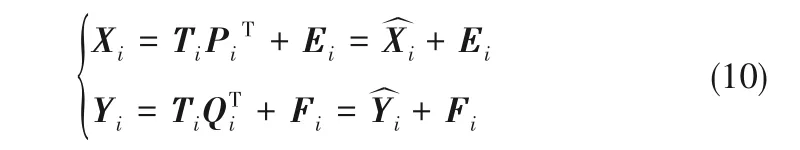
（2）训练GPR模型

①协方差函数选取：通常选用平方指数协方差函数（CovSEsio）

式中,M = diag(ell2)，ell 为方差尺度，sf2为信号方差，参数的集合hyp ={lg(ell),lg(sf)}为超参数；

②超参数初始化：设置超参数的初始值；

③超参数优化：利用优化边际可能性算法（minimize）对超参数进行优化，优化后的参数为hyp ={l,σf}；

④模型训练：似然函数选用利用高斯似然函数likGauss；推理函数选用infGausslik，用于计算后验概率。

2 Ms-NIPLS-GPR 离线建模

2.1 训练数据预处理

（1）工业过程数据中往往存在一些离群值，这些离群值在一定程度上会影响离线模型的精度，因此在离线建模前有必要将这些远离数据中心的样本点从训练模型中剔除。某一过程变量与其数据中心相似度的计算公式为

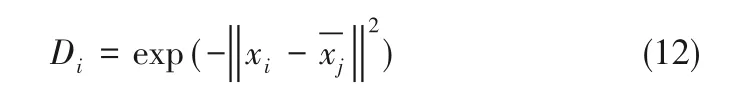
（2）根据工程经验将历史数据中运行性能稳定且区分度高的样本划分到不同性能等级的数据空间中，其标签用一组二进制数表征。通常情况下，3～4 个性能等级比较合适。当训练数据属于等级i，那么其标签（由高位到低位）的第i位为1，其余为0。例如，本文将训练数据划分为三个性能等级：最优[X1∈Rn1×m,Y1= 100]、中等[X2∈Rn2×m,Y2= 010]、较差[X3∈Rn3×m,Y3= 001]。

（3）为消除变量的量纲和单位的不同给建模带来的不良影响，需要对训练数据进行零均值、单位方差标准化处理。

2.2 Ms-NIPLS-GPR 离线模型建立

图1为离线建模的流程图，建模步骤如下：

（1）采集训练数据，进行离群值剔除、性能级分组、数据标准化一系列数据预处理。

（2）利用Ms-NIPLS 算法提取不同性能级训练数据的特征子空间，即(,),i = 1,2,3。

3 在线测试数据的性能评估

3.1 在线测试数据的状态分析方法

图1 性能等级数据离线建模过程Fig.1 Offline modeling process of performance grade data

考虑到过程扰动对在线样本数据的影响很大，所以在线评估时很难依据单个样本对当前生产过程做出准确评价[26]，故本文采用大小为H 的滑动时间窗作为基本评估单元，Xon,k=[xon,k(k - H +1),…,xon,k(k)]T。那么模型预测输出为

式中，f(·)为训练GPR模型得到的非线性映射；Yon,k=[y1,on,k,y2,on,k,…,yC,on,k]∈RH×C为k 时刻评估单元对应的GPR 输出，其中yi,on,k=[yi,on,k(k - H +1),…,yi,on,k(k)]T,i = 1,2,…,C,为GPR的第i个输出。

在基本评估单元内，当前k时刻性能与前H - 1时刻性能的相似性程度不同，所以不能单纯采用均值策略。本文采用变遗忘因子[27-28]加权计算策略，第i个输出通道在遗忘因子βj下的样本均值为

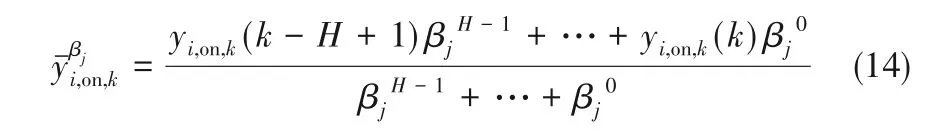
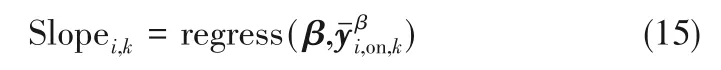
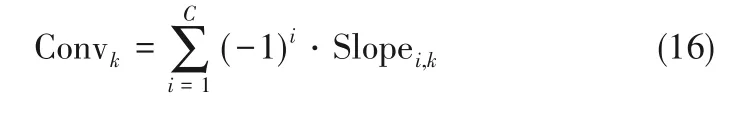
定义一个过渡态评估阈值ε，当|Convk|≤ε 时，表明数据窗口中样本性能无明显变化，性能等级与前一时刻保持不变。而|Convk|＞ε时，则表明k时刻数据窗口中样本性能发生改变，性能状态为两稳态等级之间的过渡性能状态。

3.2 在线测试数据的评估过程

在线评估过程的具体步骤总结如下。

（1）采集k 时刻的数据，与前H-1 时刻样本数据组成一个长度为H 的数据窗口，根据训练数据的均值和标准差对其进行标准化处理得到Xon,k。

（2）采用Ms-NIPLS提取特征子空间Xon,kPi。

（3）采用式(13)计算特征子空间对应的输出yon,k∈RH×C，并进一步计算,i = 1,2,…,C 和Convk来量化k时刻的性能等级和性能状态。

性能等级和性能状态评估策略如下：

Case2 如果Case1不满足，且|Convk|＞ε，则表明过程运行状态为过渡态。

Case3 如果Case1不满足，且|Convk|≤ε，则表明当前过程受不确定因素影响较大，过程运行评估结果与上一时刻的评估结果一致。

4 乙烯裂解炉系统性能评估应用

4.1 乙烯裂解炉对象描述

裂解炉是乙烯装置的核心设备，实时评估裂解炉运行状态对生产效益的提高至关重要[29-30]，而裂解炉生产过程裂解反应机理复杂，变量间存在强非线性，很难利用机理模型进行性能评估。为此，本文利用Ms-NIPLS-GPR 方法对裂解炉运行过程进行在线评估，使得裂解炉尽可能以最优性能运行。

采集裂解炉生产过程中的18个过程变量（表1）和1个质量变量——单程高附加值产品收率。本文中训练数据包含1014 组样本，根据工程经验，训练数据被分为3 个性能等级：最优[X1∈R407×18,Y1=100]、中 等 [X2∈R383×18,Y2= 010] 和 较 差[X3∈R224×18,Y3= 001]。测 试 数 据 集Xtest共 包 括1250 组测试样本，其性能的变化趋势为：最优→过渡→中等→过渡→较差。裂解炉过程模型简图如图2所示。

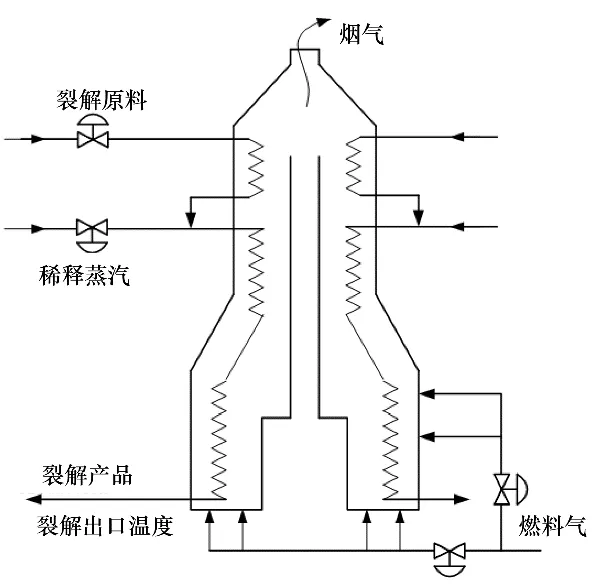
图2 乙烯裂解炉工艺Fig.2 Ethylene cracking furnace process

表1 乙烯裂解炉过程变量Table 1 Ethylene cracking furnace process variables

4.2 性能评估结果分析

图3说明了GPR 输出(y1,y2,y3)需要经过时间窗和变遗忘因子处理的必要性。图中蓝色曲线代表测试样本与最优性能等级的相似度，红色曲线代表测试样本与中等性能等级的相似度，黄色曲线代表测试样本与较差性能等级的相似度。从图3中可以看出，(y1,y2,y3)曲线波动幅度大，说明单个测试样本无法准确说明当前过程运行状态。算法中相关参数设置如下：在线评估的数据窗口长度H = 20；GPR模型超参数初值设置hyp ={0,0}；稳态评估阈值α =0.85，过渡态评估阈值ε = 0.25。

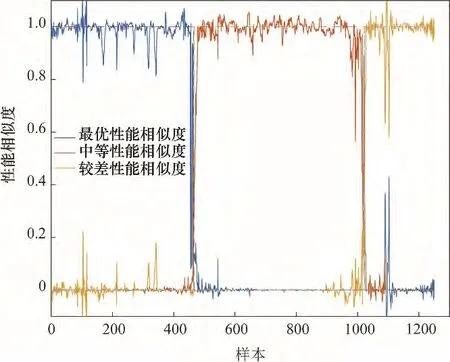
图3 不经过滑动时间窗的数据采样点各通道输出情况Fig.3 The sample curves of the channel outputs without the sliding data window

为了验证Ms-NIPLS-GPR 评估方法的准确性，将基于PCA-NN、Ms-PLS-NN 的建模方法作为对比实验。图4～图6中的横向点划线为测试样本的评估阈值α，评估曲线超过α 则认为当前过程运行在该性能等级；纵向点划线样本区域表示实际过程中过渡态的样本范围。图中(a)～(c)为相应方法得到的评估曲线，分别表示测试样本与最优、中等、较差性能等级的相似度。从仿真结果可以看出，基于Ms-NIPLS-GPR 方法的评估曲线波动较小，Ms-PLS-NN方法次之，而PCA-NN 的评估曲线波动较大。对于PCA-NN 而言，由于缺乏标签变量的引导，所以无法准确提取性能特征，抗干扰能力较弱；对于Ms-PLS-NN 而言，传统线性PLS 方法也无法完全提取非线性数据的特征；同时神经网络还具有调节参数多、过拟合等缺点，所以这两种方法在最优、较差性能等级段上有不同程度的误判，主要误判处已在图4和图5中用圆圈标明。

图7～图9 分别是在线评估结果根据式（15）、式（16）计算得到的过渡性能系数变化曲线。由仿真结果及评估策略可以得出如下结论：PCA-NN 方法将较差性能稳态部分误判为过渡态；Ms-PLS-NN、Ms-NIPLS-GPR 两种方法得到的过渡性能系数曲线相似，但基于Ms-NIPLS-GPR 方法得到的曲线在稳态部分表现得更加平稳且对于过渡状态的识别灵敏度更高，受噪声影响较小。

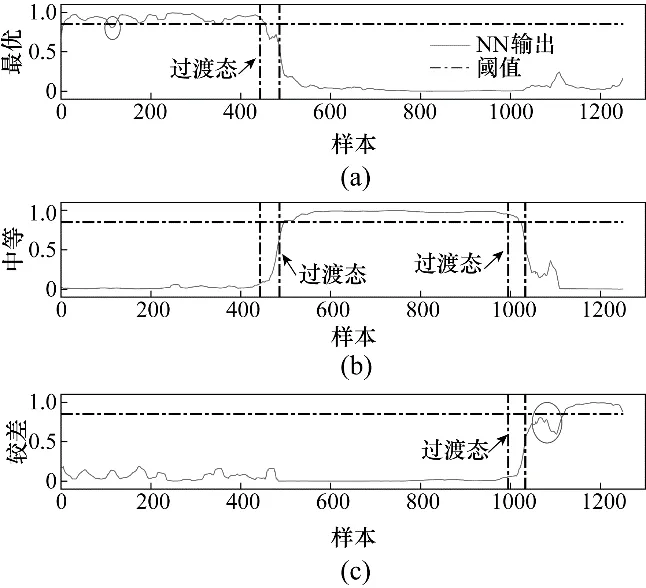
图4 基于PCA-NN的在线评估结果Fig.4 PCA-NN-based online assessment results

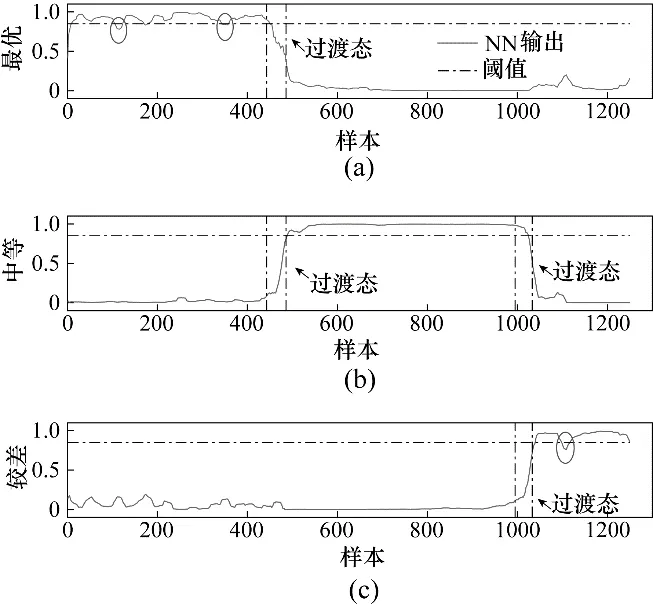
图5 基于Ms-PLS-NN的在线评估结果Fig.5 Ms-PLS-NN-based online assessment results

表2 展 示 了PCA-NN、Ms-PLS-NN 和Ms-NIPLS-GPR 方法得到的评估结果与实际情况的对比，通过定义评估准确率（评估正确样本数量与总样本数量的百分比）来判断方法的优劣。从对比结果可以看出，相较于对比方法PCA-NN 和Ms-PLSNN，基于Ms-NIPLS-GPR 计算得到的评估准确率分别提高了8.8%、4.88%，证明了本文评估方法的准确性。

5 结 论

图6 基于Ms-NIPLS-GPR 的在线评估结果Fig.6 Ms-NIPLS-GPR-based online assessment results

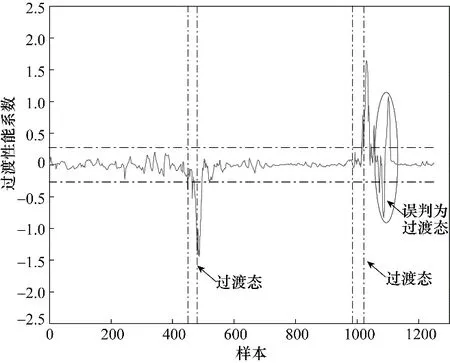
图7 基于PCA-NN的在线评估过渡性能系数曲线Fig.7 Performance transition coefficient curve based on PCANN online assessment method

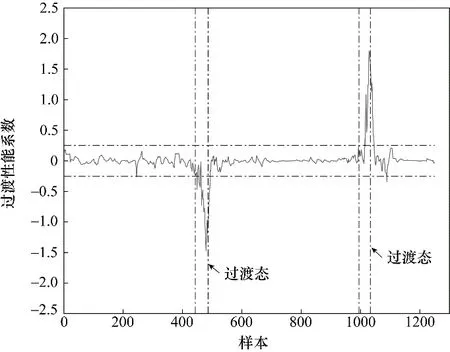
图8 基于Ms-PLS-NN的在线评估过渡性能系数曲线Fig.8 Performance transition coefficient curve based on Ms-PLS-NN online assessment method

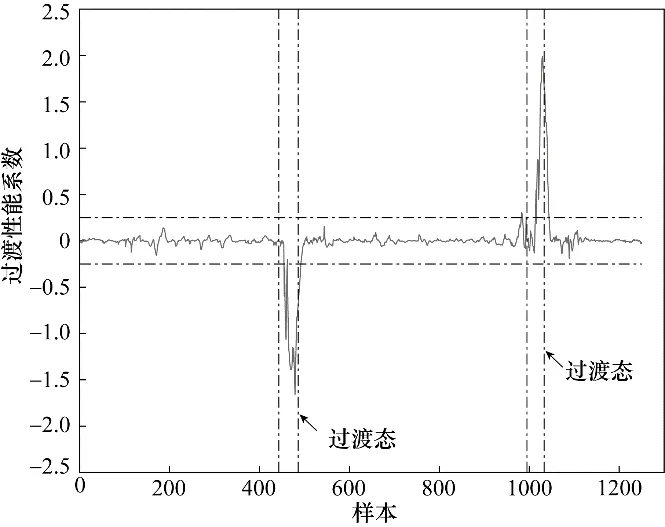
图9 基于Ms-NIPLS-GPR 的在线评估过渡性能系数曲线Fig.9 Performance transition coefficient curve based on Ms-NIPLS-GPR online assessment method

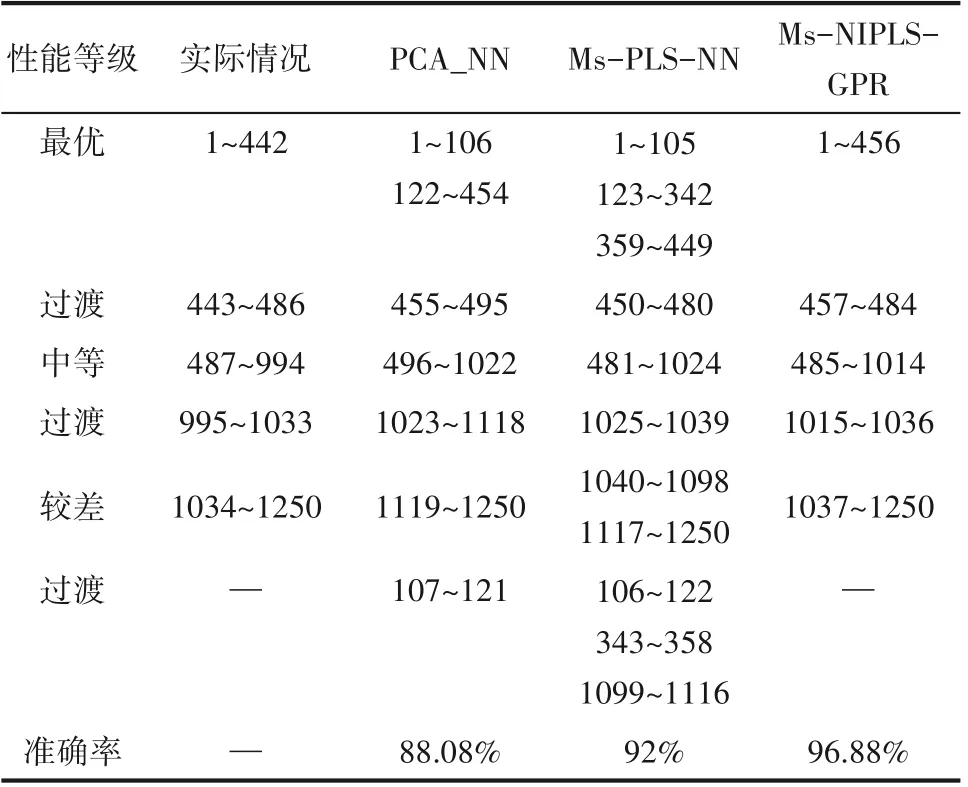
表2 在线评估结果与实际情况对比Table 2 Comparison of online assessment result and actual

针对乙烯裂解炉生产过程中过程变量与质量变量间的非线性及无关变化量难以剔除的问题，本文以多个连续性能相近的数据集作为研究对象，提出了基于Ms-NIPLS-GPR 的在线性能评估方法。离线建模阶段，通过Ms-NIPLS 算法对过程输入和输出进行分解，在适应过程数据间非线性关系的同时还最大化剔除无关变化量，提高了高斯过程回归离线模型的精度；在线评估阶段，给出了性能等级状态评估策略，在给出当前过程运行性能等级的同时判断当前过程运行状态。最后，通过比较PCANN、Ms-PLS-NN 与Ms-NIPLS-GPR 三种方法的评估准确率来说明本文评估方法的可行性和准确性。