基于改进差分进化算法的质子交换膜燃料电池模型参数优化识别
2021-04-09徐斌
徐斌
(上海工程技术大学机械与汽车工程学院,上海201620)
引 言
质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)是一种新的绿色能源,具有工作温度低、能量密度高以及绿色环保等优点,在世界范围内得到了快速的发展和广泛的应用[1-2]。由于PEMFC 系统是一类极其复杂的非线性强耦合动态系统,如何确定系统模型参数并提高模型的准确性,对提高装置的安全性和可靠性,并延长使用寿命,具有重要的意义[3-5]。
一般来说,系统模型参数识别问题可以转化为复杂非线性多维函数最优化问题[6],并采用优化方法进行求解,因此优化方法的搜索性能对模型精确性有至关重要的影响。近年来,随着智能优化技术的发展,为求解复杂优化问题提供了一种有效的方法和手段,并在PEMFC系统模型参数优化识别领域取得了较好的结果[7-8],如遗传算法[6,9]、粒子群算法[10-11]、差分进化算法[12-14]、人工蜂群算法[15]、P 系统优化[16]和声搜索[17]等。
差分进化算法(differential evolution algorithm,DE)是一种新的智能优化算法[18],具有结构简单、实现简单、鲁棒性强等特点,在化工过程优化中得到了广泛的应用[19-22]。在差分进化算法中,变异和交叉算子是两个关键的操作算子,对算法整体性能有重要的影响。因此,对变异和交叉算子的改进得到了研究人员广泛的重视,并取得了可喜的成绩[23]。如Zhang 等[24]提出了一种名为DE/current-to-pbest/1的变异策略。该策略将部分较差个体保存在一个外部存档集合中,然后基于该外部存档集合为变异操作提供更多的有利差分向量。Das 等[25]基于种群个体拓扑结构,提出一种关于局部和全局变异相结合的组合变异策略。但是该组合变异策略需要实验者提供合适的权重分配系数。Epitropakis 等[26]根据群体当前个体与群体中其他个体之间的距离为群体中每个个体分配一个选择概率,并基于该选择概率选择合适的个体参加变异操作。Gong 等[27]首先对个体进行优劣等级排序,然后根据排序结果提出了一种基于等级排序的变异策略。赵杨等[28]在多策略中选取合适的变异策略和较优的随机个体引导种群变异,同时根据进化过程信息自适应地更新交叉参数。将改进算法用于求解污水处理过程,能有效实现对溶解氧和硝态氮浓度设定值的动态寻优和跟踪控制。
本文分析了常用变异和交叉算子存在的问题,并基于文献[27]的启发,提出一种概率选择模型,并将融入差分进化算法的变异和交叉操作过程,进而提出一种新的改进的差分进化算法(IDE),提高了基本差分进化算法的搜索效率和最优结果的精度。另外进一步将改进IDE 算法用于PEMFC 系统模型参数优化识别问题,验证了改进算法的有效性和工程优化过程的实用性,同时为系统模型参数识别提供一种有效的求解方法。
1 PEMFC机理模型
1.1 PEMFC工作原理
质子交换膜是一种固态高分子聚合物膜,具有电解质的作用,并固定在多孔电极之间。通常PEMFC 系统采用氢气和氧气作为燃料和氧化剂,电子运动形成电流,驱动负载工作,反应的生成物水则会随尾气排除,如图1 所示[1]。一般情况下,在电池阳极电化学反应为:

在电池阴极电化学反应为:

则总的反应为:
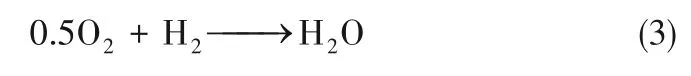

图1 PEMFC原理Fig.1 Principle of PEMFC
1.2 PEMFC数学模型
实际PEMFC 系统运行过程中,由于装置内部会存在各种内部阻力,从而导致PEMFC系统输出电压小于理想电压。因此,单电池输出电压Vcell经验计算公式为[3]:
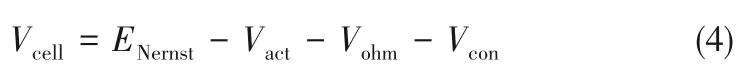
其中,ENernst表示热力学电动势,Vact表示活化过电势,Vohm表示欧姆过电势,Vcon表示浓度差过电势。
根据Nernst方程以及Gibbs自由能的变化情况,ENernst计算公式是[12]:

式中,T 表示工作温度,K;pH2和pO2分别表示H2和O2的有效分压,atm(1 atm=101.325 kPa),它们是关于当前电流值I的函数[6]:
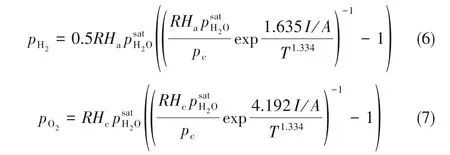

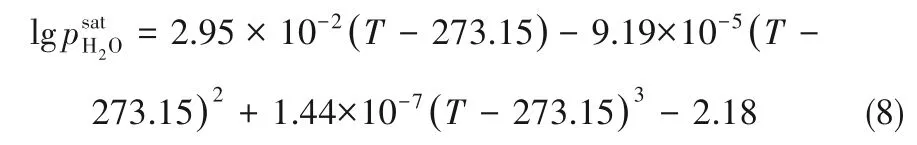
系统活化过电势Vact包括阳极和阴极处过电势,可以按式(9)计算[1,3,13]:
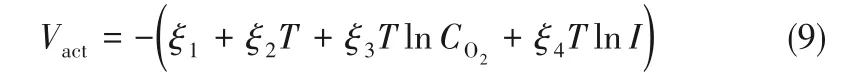
式中,ξi(i=1,2,3,4)是模型未知参数,CO2是阴极催化剂界面溶解氧气浓度,mol/cm3,其计算方法为[6]:
欧姆过电势Vohm是质子膜的等效膜阻抗产生的电势和阻碍质子通过质子膜的阻抗产生的电势,可表示为[6]:
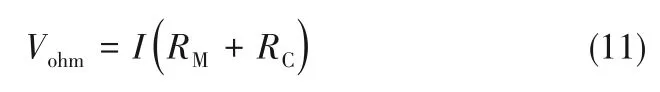
其中,RC是电子转移等效电阻,Ω;RM是质子膜等效阻抗,其计算公式为:

其中,L是质子交换膜厚度,cm;ρM是Nafion系列质子交换膜的电阻率,Ω·cm,计算公式为[14]:
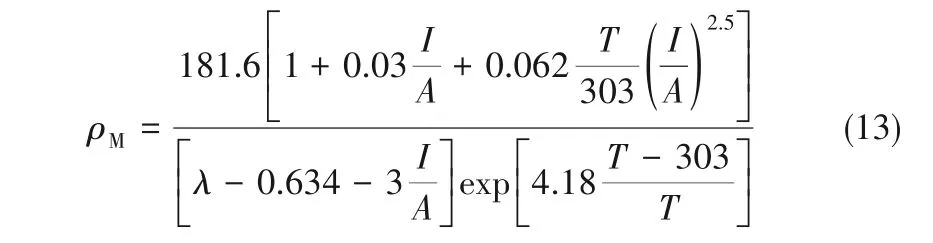
其中,λ是表示气体湿度状态信息的未知参数。
浓度差过电势Vcon是由于物质扩散阻力的存在导致反应物浓度变化产生的电势,计算公式为:
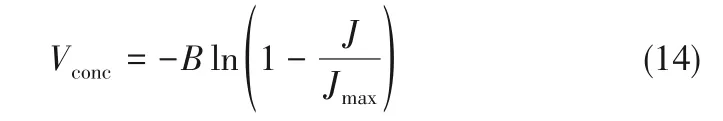
其中,B 是关于电池工作状态的未知参数,V;J是电池实际电流密度,A/cm2,Jmax是实际电流密度的最大值。
为了提供充足的持续电量,实际PEMFC系统是由多个电池串联组成的电池堆,NS个电池串联构成的PEMFC电池堆终端输出电压为:

1.3 优化数学模型
从PEMFC 模型可以看出,系统模型中存在一些难以确定的未知参数,即ξ1、ξ2、ξ3、ξ4、λ、RC和B。为了确定这些参数的最优值,选择实际输出和模型输出数据的误差平方和为优化目标函数[29-30]:
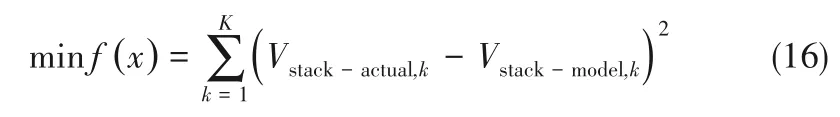
其中,Vstack-actual是实际电池堆输出电压值;Vstack-model是系统模型输出电压值,它是关于未知参数x =[ξ1,ξ2,ξ3,ξ4,λ,RC,B]T的函数;K 是样本数据个数。系统工作参数和未知参数的实际值以及对应的搜索范围可参考文献[13]。可以看出,当系统模型越加接近实际输出时,目标函数值越小,理想情况下,当系统模型输出等于实际输出时,目标函数取得最小值零。
2 基本差分进化算法
差分进化算法是一种新的启发式搜索算法,主要用于求解连续优化问题[18]。不失一般性,对于给定的D维优化问题:


2.1 变异操作
变异操作存在多种不同形式的策略,最为经典和常用的策略是:
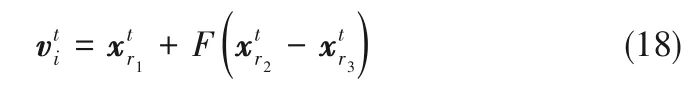
其中,r1、r2和r3是区间[1,N]内与i不等的随机整数,且满足两两互不相等;缩放因子F是在区间(0,1]内的正实数。
2.2 交叉操作
交叉操作主要完成变异后向量和父代向量信息交换,增加种群的多样性。最常用的二项式交叉表示为:

其中,sn∈[1,…,D]是一个随机整数。交叉参数CR一般是区间[0,1]之间的实数。
2.3 选择操作
选择操作在父代向量和交叉后向量之间实行贪婪选择,计算公式是:

3 改进差分进化算法
3.1 个体概率选择模型
假设群体含有N 个个体,首先按目标函数值从小到大进行排序,然后根据排序结果计算每个个体的选择概率为:
其中,r(i)表示第i个个体对应的排序等级。可以看出,对于种群中所有个体,最优个体具有最大的选择概率,最差个体具有最小的选择概率。
在确定每个个体的选择概率之后,根据概率大小从群体中选择个体参与变异操作和选择操作。这里采用最为常见的轮盘赌选择方式。首先计算每个个体的累积选择概率:
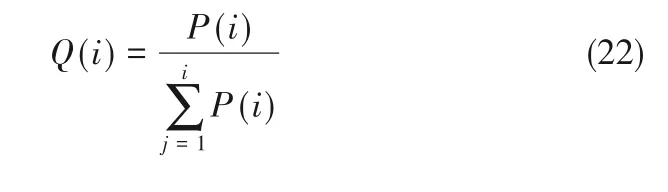
然后在区间[0,1]之间产生一个均匀分布的伪随机数r;如果r<Q(1),则选择第1 个个体,否则,令k=k+1,直到条件Q(k-1)<r≤Q(k) 成立,同时选择个体k作为最终选择结果。
3.2 基于概率选择的变异算子
在计算选择概率后,采用概率选择方式代替传统随机选择方式选择群体中个体参加变异操作。适用于DE/rand/1 变异策略的个体概率选择过程如下:
(2)While r1=i;
(5)While r2=r1or r2=i;
(8)While r3=r1or r3=r2or r3=i;
可以看出,与标准差分进化算法相比,基于概率模型的变异算子最大的特点是个体和个体的选择。值得注意的是这里个体选择仍采用随机方式,主要原因是(-)可以看成是方向向量,当以概率方式提供,而以随机方式提供时,可以得到更丰富的梯度下降方向,加快算法的收敛速度。
3.3 基于概率选择的交叉算子
在经典二项式交叉的基础上引入概率选择操作。对于每个父代个体,以概率选择方式选择一个个体与实施交叉操作。计算方式如下:
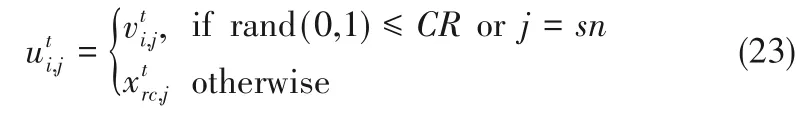
从计算公式可以看出,变异后个体与概率选择的个体交换信息,这样可以让更多的优秀基因保留到下一代群体,加快算法的收敛速度和求解精度。
基于上述概率选择模型以及对应的改进变异、交叉算子,本文IDE算法流程下:
输入:算法参数N,F,CR,T;
随机产生初始种群X0并计算目标函数值;
While t<T
计算种群中每个个体的选择概率Q;
For i=1∶N
If rand(0,1)<0.5
Else
按式(23)实施交叉操作;
Else
按式(19)实施交叉操作;
For i=1∶N
t=t+1
输出:当前群体中的最优个体。
可以看出,本文IDE 算法和文献[27]类似。但是,它们是不同方法,主要区别是:(1)文献[27]仍然采用随机选择方式选择个体参与变异操作,选择概率仅用于判断被选个体是否满足要求。本文IDE算法直接利用概率选择方式选择个体,但仍采用传统方式判断被选个体是否满足要求。(2) 本文IDE 算法将概率选择模型应用于变异和交叉操作,而文献[27]个体概率仅用于变异过程,交叉过程仍采用标准的二项式交叉方式。(3)本文概率选择模型仅用于部分个体,而文献[27]中改进变异算子作用于所有个体。
4 算法测试和分析
为了验证IDE算法的有效性,将其与标准DE进行比较,选择Fsph、Fros、Fack、Fgwr、Fras、Fsch、Fsal以及Fwht这8 个常用的标准测试函数进行试验仿真[31]。两种算法参数设置如下:种群规模N=50,问题维度D=30,缩放因子F=0.6,交叉参数CR=0.5,最大迭代次数T=1000。为了减少算法的随机性,每个问题采用相同的初始群体,并独立运行25 次,计算最小值、最大值、中位值、平均值以及标准方差。
表1 给出了两种算法求解8 个标准测试函数得到的统计结果。从表中可以看出,相比标准DE 算法,IDE 算法得到的最优结果要比标准DE 算法结果更好,也更加接近真实最优值,特别是对于函数Fsph、Fack、Fgwr和Fsch,效果更加显著。为了更加直观显示两种算法在求解这些问题时表现的收敛能力,图2给出了25 次独立运行结果中位值对应的收敛曲线图。从图中可以看出,IDE 算法对于所有问题,表现出较快的收敛速度以及精度,同时对于部分问题,如Fsch,能以一定概率跳出局部最优值。因此,基于概率选择模型的变异和交叉算子在提高差分进化算法的收敛速度的同时,也能提高求解精度,是一种有效的提高差分进化算法性能的方法。

表1 两种算法求解基准函数的测试结果对比Table 1 The comparison results of two algorithms over benchmark functions
为了展示改进算法在不同种群规模下的有效性和稳定性,表2 给出了DE 和IDE 这两种算法在不同种群规模条件设置下计算结果平均值。从表中可以看出,对于DE 和IDE 算法,当种群规模从50 增加到400 时,IDE 算法除了在求解Fgwr问题时均值出现一定波动,在部分种群规模情况下效果较好之外,对于其余问题没有显著的变化。至于基本DE算法,当群体规模发生变化时,均值变化不是很大。因此可以认为群体规模在一定程度上对算法性能影响不明显。
5 实例研究
本文采用改进IDE算法求解质子交换膜燃料电池模型参数优化识别问题,如式(16)所示。该问题较为复杂,无法直接求解梯度等相关信息。因此,本文中选择目前较为主流的实数编码遗传算法(RCGA)、粒子群算法(PSO)、人工蜂群算法(ABC)等几种典型智能优化算法进行比较与分析。

图2 两种算法迭代收敛曲线图Fig.2 Convergence graphs of two algorithms
在无噪声、低噪声和高噪声三种不同情况下进行实验仿真,不失一般性,含有噪声的输出电压值计算为[13]:
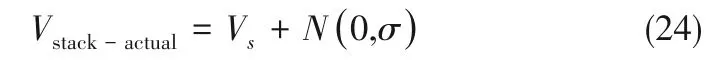
其中,Vs为无噪声条件下的输出电压值,N(0,σ)代表均值为0、方差为σ 的高斯白噪声。无噪声、低噪声和高噪声三种不同情况下方差取值分别为0、1/6 和1/3。五种算法参数设置如下:种群规模N=50,最大迭代次数T=100。对于遗传算法,交叉概率pc=0.9,变异概率pm=0.9。对于粒子群算法,学习因子c1=c2=2,采用动态惯性权重。对于差分进化算法,缩放因子F=0.6,交叉参数CR=0.5。
表3 给出了五种算法在三种不同情况下25 次独立运行得到的最优结果。在无噪声环境,IDE、DE以及RCGA 算法得到的结果较好,而PSO 和ABC 表现稍差,目标函数相差1~2 个数量级。在低噪声和高噪声环境下,IDE、DE、ABC 和RCGA 表现较好,PSO 表现稍差,目标函数相差1 个数量级。总体来说,三种不同环境下采用IDE 算法得到的最优参数都接近真实最优值,对应的目标函数值最小,表现最优。
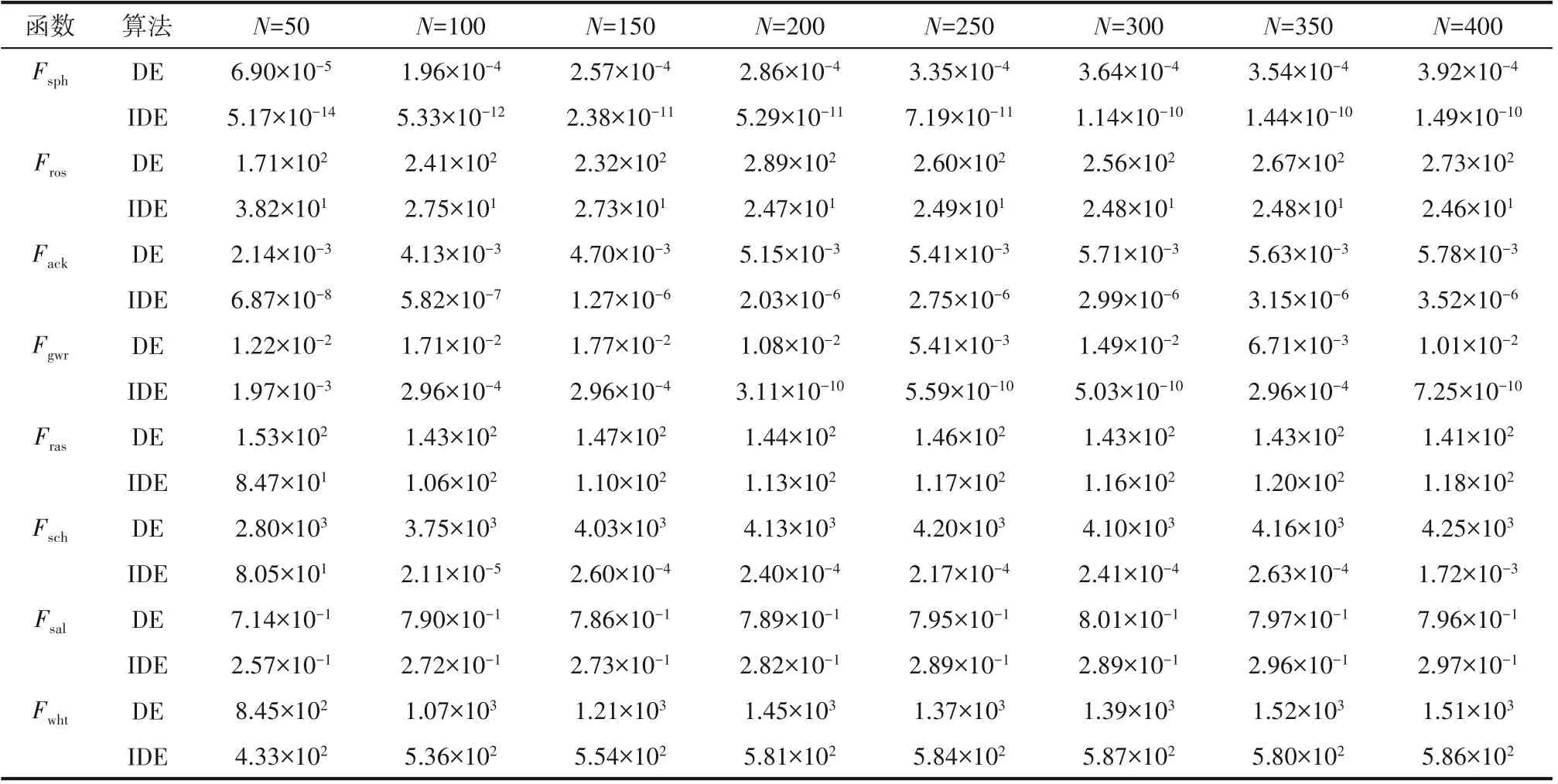
表2 不同群体规模下测试结果Table 2 Experimental results with different population size
为了更直观地显示IDE算法优化系统模型的有效性,图3 给出了实验数据和IDE 算法优化模型输出电流-电压曲线图。从图中可以看出,对于无噪声情况,优化模型输出曲线几乎与实验数据保持一致。对于存在噪声的情况,系统电流-电压曲线图也能与实验数据保持一致。结果表明,优化系统模型能较好地反映实际系统。
6 结 论
本文基于概率选择模型提出了一种改进的差分进化算法并用于质子交换膜燃料电池模型参数优化识别过程,结论如下:
(1)在差分进化算法个体选择方面建立了个体概率选择模型,并将该概率选择模型应用于差分进化算法的变异和交叉操作过程,提高了算法的搜索效率和求解精度。

表3 五种算法在三种情况下求解最优结果比较Table 3 The best results of five algorithms under three different conditions
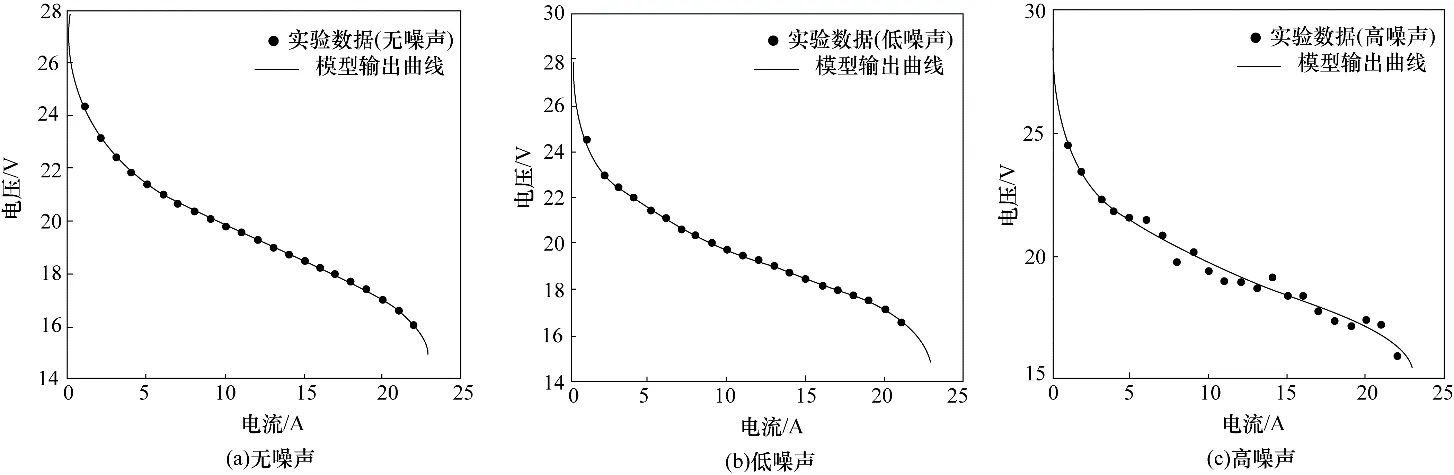
图3 实验数据和模型输出曲线比较Fig.3 Comparisons between the simulated data and the model curves
(2)根据最小误差平方和原理得到了关于模型未知参数的数学模型,然后将改进算法用于求解质子交换膜燃料电池模型参数优化识别问题,取得了满意的结果。
(3)概率选择模型仅应用于变异和交叉操作过程,后续将进一步推广,将其应用于算法其他操作算子中,并应用于其他类型参数最优识别问题中,验证其在工程优化中的一般性和普适性。
符 号 说 明
NS——电池个数
u——交叉后个体
v——变异后个体
x——主种群个体
