基于MIC的支持向量回归及其在化工过程中的应用

顾俊发，许明阳，马方圆，林治宇，纪成，王璟德，孙巍

（1 北京化工大学化学工程学院，北京100029； 2 中化泉州石化有限公司，福建泉州362103）

引 言

在化工生产中，某些关键变量可以直接或间接地反映过程的运行状态，对于操作人员判断装置的运行情况十分重要。但受测量手段或仪表故障等因素的影响，这些关键变量可能出现无法实时获取或读数异常的问题。此时，软测量技术可以通过提取历史数据中关键变量与其他变量间的关系，建立回归模型，实现对关键变量的预测[1]。在建立软测量模型时，辅助变量和回归方法的选取会直接影响到模型的预测效果[2]。化工过程中变量众多，如果将所有相关变量全部作为输入建立软测量模型，不仅会导致数据的冗余，增加模型运算量，也会造成模型的预测准确率降低[3]。目前常利用Person 系数等线性相关度量准则分析过程变量与软测量目标变量间的关系，选择合适的辅助变量[4]，然后利用线性回归模型提取变量间关系，建立软测量模型，实现对关键变量的实时预测。常见的线性回归方法有岭回归、偏最小二乘法等[5]，其优点在于计算简单且可解释性强，对稳态过程具有较强的适用性[6]。但在实际化工生产中，装置并非一直处于稳态过程，而且绝大多数变量间的关系十分复杂，为非线性关系。相比于利用线性相关度量选择变量建立线性模型，如果能够在综合考虑变量间线性和非线性关系的基础上建立软测量模型，则应能够实现对目标变量更好的预测。

最大信息系数(maximal information coefficient，MIC)是一种基于信息论的度量标准，利用互信息和网格划分的方法来计算变量间的相关度，同时考虑了变量间的线性和非线性关系，具有适用性广、计算简单等优点，适用于非线性回归模型的变量选取。同时，支持向量回归(support vector regression,SVR)方法是一种常用的非线性回归方法，在结构风险最小化原则基础之上发展起来，能够根据数据信息在模型学习能力和复杂度之间寻求最优性能，以获得良好的推广能力，有较强的泛化能力，能够对目标变量做出较为准确的预测[7]。

基于此，本文提出了一种基于MIC 的支持向量回归软测量方法，利用最大信息系数度量过程变量与软测量目标变量间的相似度，选择合适的辅助变量，避免了全部变量作为输入所造成的数据冗余。在此基础上，利用支持向量回归方法提取辅助变量与软测量目标变量间的关系，建立软测量模型，实现对软测量目标的预测。该方法被应用于存在仪表故障的某催化重整装置进料换热器热端压降的软测量中，结果表明该方法可以有效地实现对压降的预测，实现对仪表故障时的数据校正。

1 方法原理

1.1 最大信息系数

最大信息系数是Reshef 等[8]于2011 年首次提出的一种基于互信息理论的最大信息系数，它可以有效监测变量间的线性或非线性关系，是较好的衡量变量间相关性的指标。

1.1.1 常见相关性度量方法对比 常见的相关性度量方法及其特点如表1所示，从表中不难看出，与其他常见的相关性度量方法相比，MIC 方法具有适用范围广、鲁棒性强、计算复杂度低等优点[9-11]。

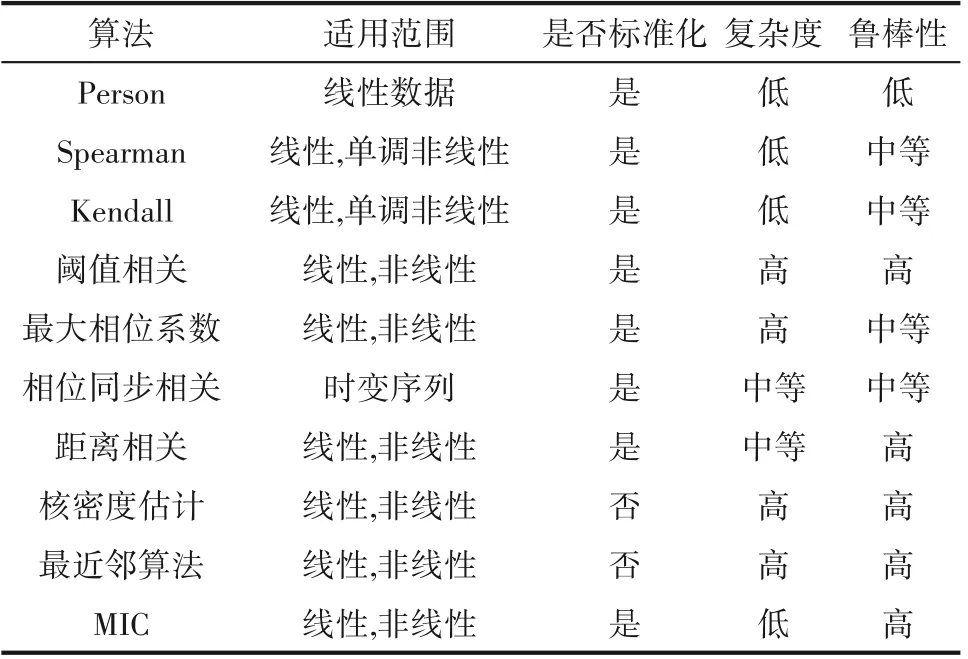
表1 相关性度量方法Table 1 Correlation measurement algorithm

1.1.2 MIC 原理 MIC 利用互信息和网格划分的方法来进行计算，其中互信息可以看作是一个变量中包含的关于另一个变量的信息量，互信息计算公式如式(1)所示：

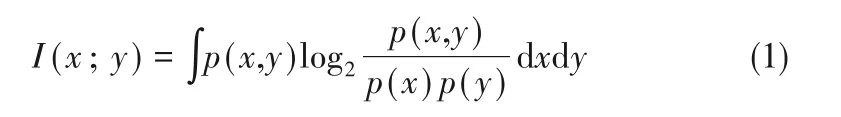
其中，p(x,y)为x,y之间的联合概率。给定一个有限的有序数据集，如式(2)所示：

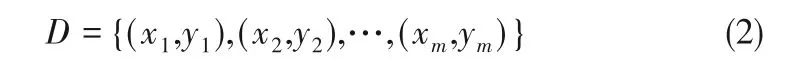
将集合D 中x,y 构成的散点图进行(a,b)的网格划分，然后查看当前的散点在各个方格的落入情况，分别计算每个网格中的互信息，网格的划分方式还有很多种，选取不同方式下互信息的最大值,得到最终的MIC，计算公式如式(3)所示：

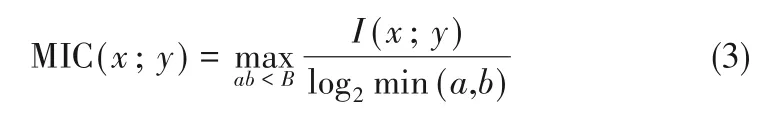
其中，a, b 是在x, y 方向上划分格子的个数，B为网格划分的上限值。

1.2 支持向量回归

支持向量回归是一种基于统计学理论的机器学习方法，在解决非线性问题上有很好的效果，被广泛应用于工业界各个领域[12]。

1.2.1 常见软测量方法比较 基于数据驱动的软测量方法主要包括线性方法与非线性方法两大类。常见的线性方法包括偏最小二乘法(PLS)、岭回归方法(Ridge)，其优点是计算简单，可解释性强，适用于稳态过程[13-17]。常见的非线性方法包括支持向量回归(SVR)、神经元网络等，其优点在于能够适用于复杂的非线性过程[18-20]。常见的软测量回归方法及其优缺点如表2 所示，化工过程中经常伴随着状态调整，为非稳态过程，存在着线性与非线性关系。支持向量回归具有非线性优势，且有较强的泛化能力，优势明显。

1.2.2 SVR 原理 对于如式(4)所示给定训练集样本M，希望得到一个回归模型使得f(x)与y 尽可能接近，w、b是待确定的回归参数，假设能容忍f(x)与y之间最多有ε 的偏差，SVR 问题可以转化为如式(5)所示:

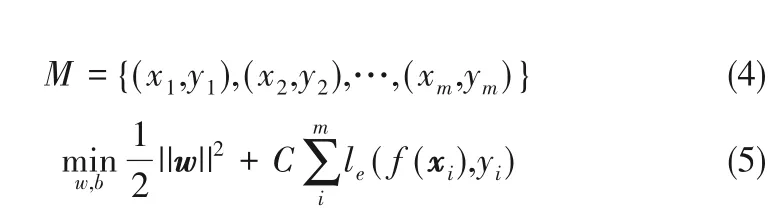
其中C 是正则化参数，le是不敏感损失函数，如式(6)所示。

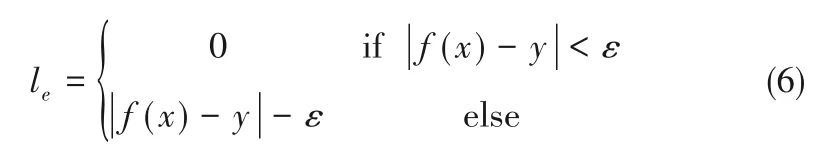
引入松弛变量ξi和ξ*i后，式(5)可重写如式(7)所示。

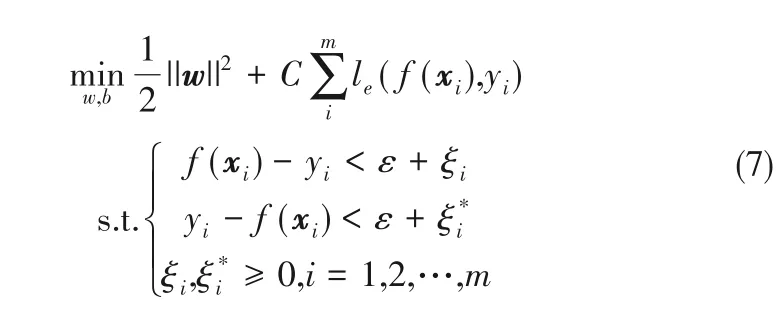
引入拉格朗日乘子μi后，将其转化为对偶问题。

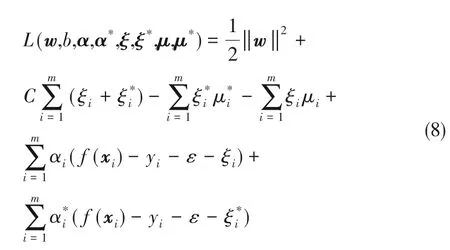
令L 对w, b,ξ,ξ*的偏导数为0，即可对w 和b 进行确定[21]。得到最终的SVR解形式如式(9)所示：

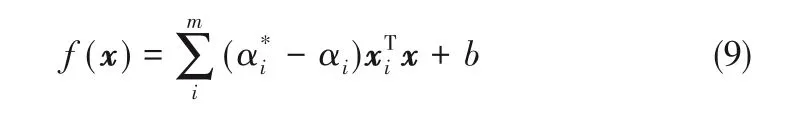
1.2.3 核函数引入 上述情况是线性可分的，对于线性不可分情况，可以将样本从原始空间映射到一个更高维的特征空间，使得样本在这个空间线性可分，但是特征空间维数可能很高甚至是无穷维的，直接计算是十分困难的，为了避免这个障碍，引入了核函数[22-23]

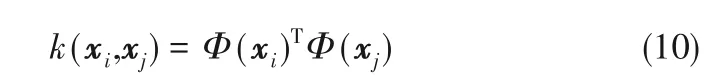
通过核函数就可以用原始空间数据的计算结果来计算特征空间上的内积，避免了上述的障碍。这样SVR解形式就可以改写为式(11)所示形式。

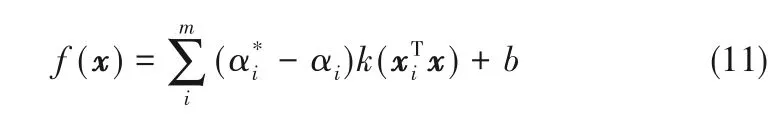
1.3 基于最大信息系数的支持向量回归方法

基于最大信息系数的支持向量回归（MICSVR）算法框图如图1 所示，首先通过对原始数据各变量间MIC 值的计算，确定与目标变量相关性较强的辅助变量。在确定辅助变量之后将数据归一化划分为训练集与测试集，接着对模型进行训练优化模型参数，得到最终模型并对测试集进行测试。

表2 常见软测量方法Table 2 Soft measurement method

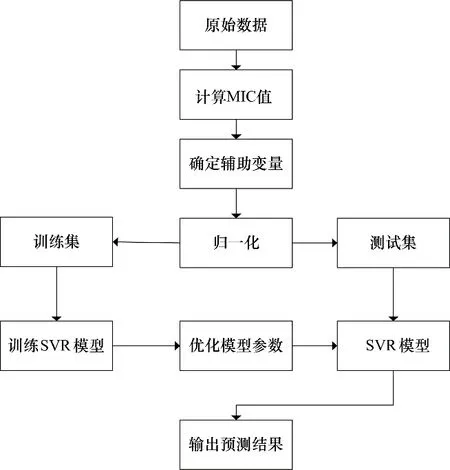
图1 MIC-SVR算法框图Fig.1 The diagram of MIC-SVR algorithm

1.4 性能指标

1.4.1 决定系数（coefficient of determination，R2） 在回归模型中用于评估预测值和实际值的符合程度, R2越接近于1，符合程度越高[24]，计算公式如式(12)所示：

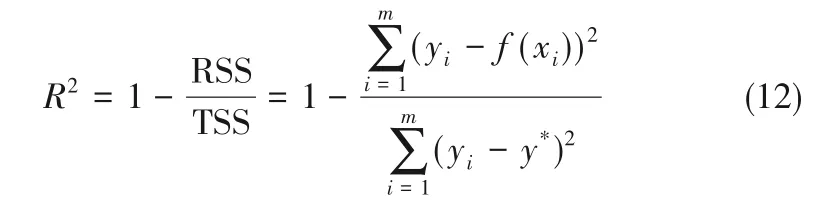
其中，f(x)是预测值，y 是实际值，y*是实际值的平均值，RSS是残差平方和，TSS是总平方和。

1.4.2 均方根误差（root mean square error，RMSE） 用来衡量观测值同真值之间的绝对偏差[25]，计算公式如式(13)所示：

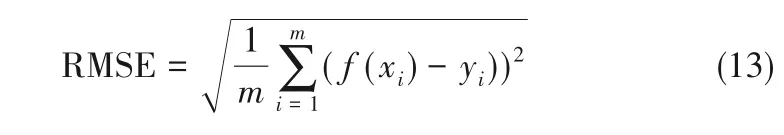
1.4.3 相对误差率（relative error rate，S） 用于衡量观测值与真实值之间的相对偏差[26]，计算公式如式(14)所示：

其中，f(x)是预测值，y 是实际值，y*是实际值的平均值。

2 实例研究

国内某大型石化公司的催化重整装置，重整进料换热器的热端压降可以间接地反映出换热器内部的结垢情况，当换热器内部的结垢多时则需要进行在线冲洗，如果不能够及时在线冲洗，轻则会影响换热效率，增加企业的运行成本，严重时可能会导致生产安全事故的发生[27-28]。但在实际生产中，测量仪表可能存在仪表错误的情况，这会导致操作人员无法判断换热器的运行状态，因此对于换热器压降的实时预测以及及时的数据校正显得尤其重要。因此考虑对热端压降进行MIC-SVR 软测量模型的建立。

2.1 辅助变量的选取

首先根据实际工业过程选取了27 个与换热器热端压降相关的变量，计算各个变量与重整进料换热器热端压降的MIC值，如表3所示。

表3 最大信息系数计算结果Table 3 The result of MIC

取各个计算结果的均值，将MIC 值大于均值的变量筛选出来，共得到12个变量，如表4所示。

2.2 模型的建立

2.2.1 模型参数 模型参数主要包括两部分：一个是核函数参数；二是超参数惩罚因子C 和不敏感损失系数ε[29-30]。

2.2.2 参数的确定 首先将所选数据集进行归一化，将归一化的数据按照7∶3 的比例划分为训练集和测试集。

本次所选用的核函数是高斯核函数,如式(15)

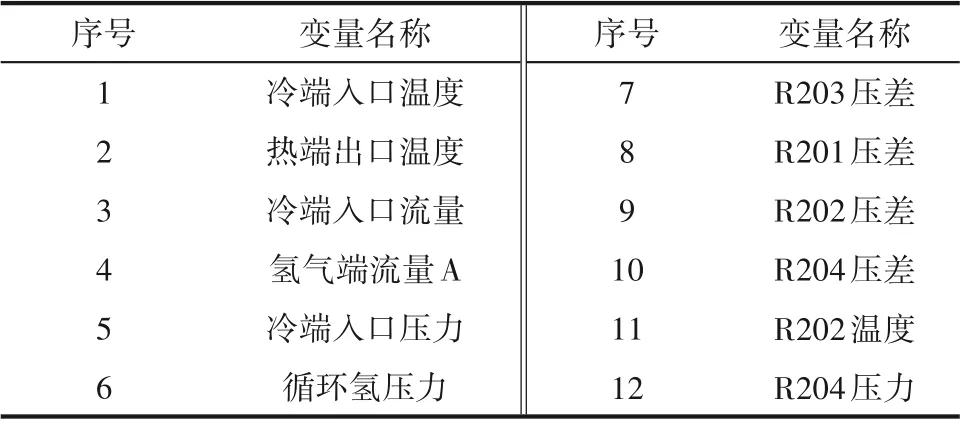
表4 辅助变量表Table 4 Auxiliary variable table

所示：

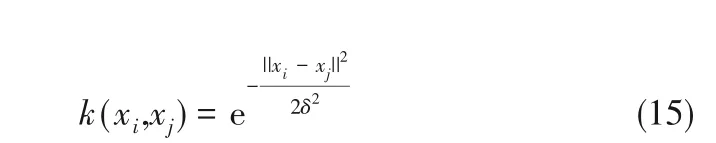
其本身参数只有一个δ，构造一个从0.01～10 的长度为20 的等比数列，探究δ 值在哪个范围内测试集效果较好，结果发现δ 在0.1～1 之间效果最好，再构造一个从0.1～1的长度为20的等差数列进行更为精准的参数确定，得到最终的δ=0.24。

接着对模型的超参数进行确定，将惩罚因子C和不敏感损失系数ε进行排列组合确定最佳的超参数组合，最终确定C=6.952,ε = 0.015。由此热端压降的MIC-SVR软测量模型建立完毕。

2.3 模型预测结果与讨论

将测试集数据代入建立好的软测量模型，对压降进行预测，得到预测值与真实值情况如图2所示，R2=0.8569,RMSE=0.2770,S=0.25%,拟合效果较好。

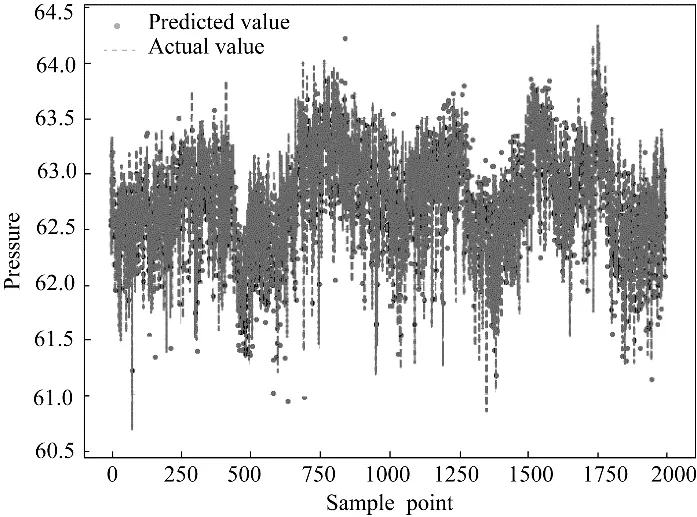
图2 测试集预测结果Fig.2 The prediction of test data

采用相同的数据集，不同的建模方法对比结果如表5 所示，从表中可以看出SVR 预测结果要好于传统的PLS 方法,在采用了MIC 方法选取辅助变量之后PLS和SVR预测结果均有显著提升。

在实际生产过程当中，热端压降出现仪表异常的情况，但仪表读数的准确性对于整个生产过程显得尤为重要，现对仪表异常情况进行软测量并进行数据校正，保证生产过程数据的准确性。如图3 所示为仪表发生超量程异常的情况，此预测结果可以实现对仪表数据的校正。

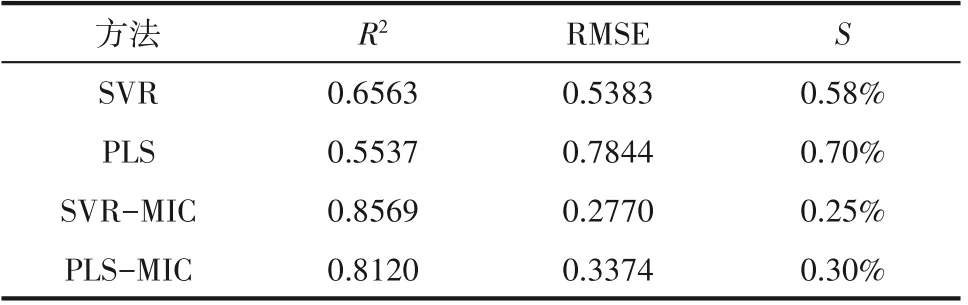
表5 不同算法预测结果Table 5 The prediction of different algorithms

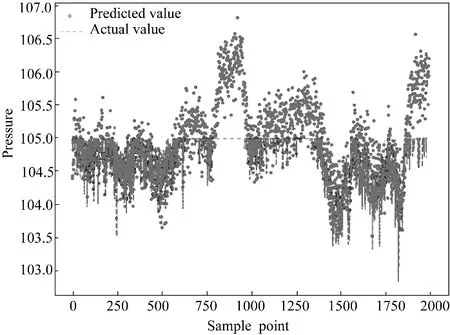
图3 仪表异常情况预测结果Fig.3 The prediction of faulty sensor

3 结 论

本文针对实际过程当中，由于仪表故障而无法实时获取数据的问题。提出了MIC-SVR 软测量方法，并与线性方法PLS进行比较，结果表明非线性的SVR 更适合于复杂的工业过程。另外与未经变量选择的模型也进行了对比，结果表明经过变量选择的模型优于未经变量选择的模型，说明在建模过程中进行变量选择可以提高模型的泛化能力和降低模型的复杂度。最后将MIC-SVR 应用于存在仪表故障的某催化重整装置进料换热器热端压降的软测量中，实现了对异常仪表的数据校正。

符 号 说 明

b——阈值

C——惩罚因子

f(x)——预测值

I——互信息

MIC——最大信息系数

m——观测值数量

p(x,y)——x,y之间的联合概率

R2——决定系数

RMSE——均方根误差

RSS——残差平方和

S——相对误差率

SVR——支持向量机回归

TSS——总平方和

w——权重向量

y——真实值

α,μ——拉格朗日乘子

ε——不敏感损失系数

ξ——松弛向量