基于代理模型的含盐废水多级纳滤系统的过程优化设计

陆至彬，谢星，鲁思达，何畅，张冰剑，陈清林

（1 中山大学材料科学与工程学院，广东广州510275； 2 西安航天源动力工程有限公司，陕西西安710000；3中山大学化学工程与技术学院，广东珠海519082；4广东省石化过程节能工程技术研究中心，广东广州510275）

引 言

煤化工废水“零排放”是破解现代煤化工产业可持续发展与环境污染矛盾的重要途径[1-2]。零排放方案的重要末端工序是集中回收在废水处理、循环水冷却等过程中不断累积的无机盐混合物，包括Na+、Ca2+、Cl-、SO2-4等离子。上述离子主要以一价盐NaCl 和二价盐Na2SO4形式析出，总浓度范围通常在500～6000 mg/L。但是，传统的废水零排放方案忽视了不同价态盐离子的差异性，通常直接利用“膜法/热法+结晶”将所有盐离子一并回收，导致浓缩结晶后的杂盐丧失了重复利用和资源化的价值。同时，杂盐中通常会残留微量的有机物和重金属离子，在储存过程中遇水容易渗出而带来二次污染风险，导致其可能具有危险废弃物的特性[3-4]。因此，对煤化工含盐废水中的杂盐进行有效分离和回收是现代煤化工产业可持续发展所亟需解决的关键问题之一。

目前，煤化工所涉及的零排放技术涉及两类分盐结晶工艺[5]：一是利用废水中无机盐的浓度和溶解度差异的热法结晶分盐工艺；二是利用Cl-和SO2-4的离子半径或电荷特性等差异的膜法分盐结晶工艺，这也是当前含盐废水处理的研究热点。纳滤(nanofiltration,NF)是一种性能介于反渗透和超滤之间的膜分离过程，其分离能力取决于膜的孔径和表面电荷性质[6-7]。由于膜的带电表面会产生电排斥效应，带负电荷的纳滤膜能有效地排斥高价离子，而对一价离子的截留能力较低[8-9]。尽管如此，但单级的纳滤系统往往得不到理想的分盐效果，纳滤卤水中氯离子的比例仍然很高，不利于后续硫酸钠的结晶过程，因此多级纳滤系统是提高分盐效果的有效途径。

为深入探究离子运输和分离现象的内在复杂机理，构建高保真的纳滤预测模型一直是研究热点领域之一。2002 年，Bowen 等[10]提出道南细孔模型，并引入介电排斥加以完善，形成道南细孔-介电DSPM-DE 模型，为发展纳滤模型奠定了理论基础。近年来，DSPM-DE 模型已被成功应用于解释和模拟各种进料条件下的纳滤性能。例如Geraldes 等[11]开发出开源程序NanoFiltran，对于纳滤过程的模拟研究有重要的意义。Pérez-González 等[12]从实验和理论上研究了纳滤在高浓度盐水溶液中分离硫酸盐/氯化物的效果，其后Ortiz-Albo等[8]使用流动电位测量法对此作了详细分析。Roy等[13]利用DSPM-DE模型对平板膜和卷式膜组件进行了详细的建模并验证其在海水纳滤中的应用。但DSPM-DE 理论模型内在的复杂性严重限制了其在复杂分盐系统建模和优化方面的应用，因此有必要寻找合适的模型简化手段来降低模型的维度和复杂度，从而有利于后续系统分析和优化进程。

基于DSPM-DE 理论模型，本工作将构建能准确描述煤化工含盐废水纳滤传质的高保真代理模型。为了增加代理模型的可移植性，先通过高维模型表征(HDMR)的手段建立数据驱动模型，可在一定范围内准确预测纳滤透过液的离子浓度。将训练好的代理模型嵌入多级纳滤系统优化中，以分离单位质量NaCl的比能耗为优化目标，通过求解非线性模型，揭示在给定设计参数的条件下进料液中[Cl-]/SO2-4]的变化对不同级数纳滤系统的性能及最优操作条件的影响。

1 纳滤膜传质机理模型

本文使用的DSPM-DE 模型被认为是描述纳滤膜传质的较为成熟的理论模型[14-15]。纳滤膜活性层的离子渗透通量可以通过扩展的Nernst-Planck 方程来描述[13]，见式(1)～式(2)：

式中，j为离子通量，mol/(m2·s)；D 为离子扩散系数，m2/s；C为离子浓度，mol/m3；Di,∞为第i种离子在无限稀释溶液中的扩散系数，m2/s；z 为离子化合价；Jw为溶剂(水)的跨膜渗透通量，m/s；φ 为膜孔内电势，V；R为理想气体常数，8.314 J/(mol·K)；T为热力学温度，K；F 为法拉第常数，96500 C/mol；x 为沿着膜孔通道轴向方向的位置，m；下角标，i 和pore 分别表示离子种类和膜孔。考虑到孔内传质阻力，此方程引入了修正的扩散阻力系数Ki,d和对流阻力系数Ki,c，其取值与离子的Stokes半径ri和膜孔半径rpore的比值λi有关[16]。

在膜与进料溶液界面处，考虑到浓差极化的影响[17]，式(1)改写为

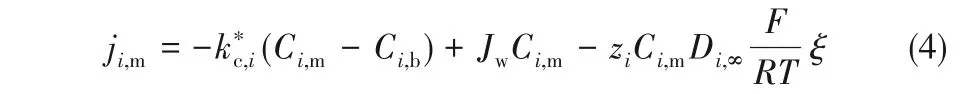
由于纳滤膜为带电膜，故膜孔内电荷平衡需要考虑膜电荷密度(Xd)，从而膜孔内、膜/进料液界面处、透过液的电中性条件分别由式(5)～式(7)约束：

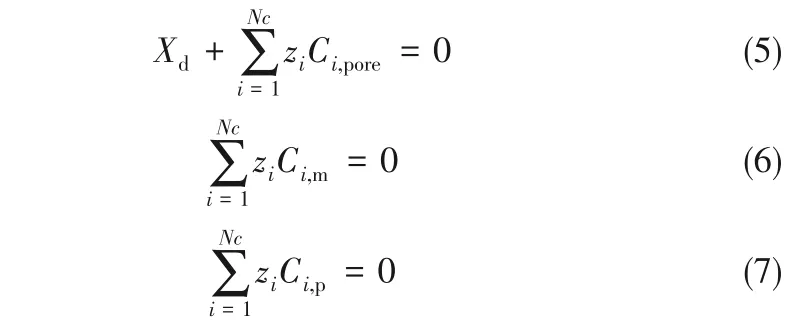
式中，Nc 为离子种类的总数目；Ci,p为透过液的离子浓度，mol/m3；下角标，p表示透过液。

由于空间位阻、道南效应和介电效应的综合影响，膜两侧与溶液界面的平衡边界条件由式(8)～式(9)给出[19]：

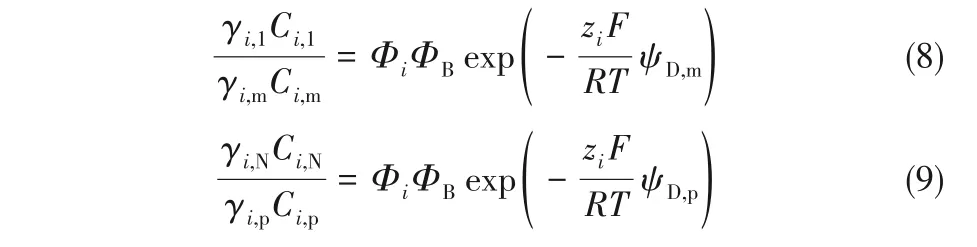
式中，ψD为平衡时膜上形成的道南电位，V；Ci,1和Ci,N分别为进料液和透过液与膜的界面处膜孔入口和出口的离子浓度，mol/m3；γi为溶质活度系数；Φi和ΦB分别指空间分配系数和波恩溶剂化系数，可根据式(10)～式(12)计算：

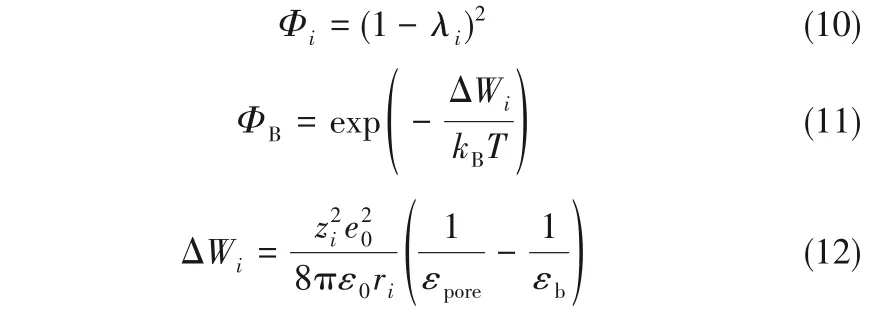
式中，ΔWi为波恩溶剂化能垒，J；kB为Boltzmamn常数，1.380648×10-23J/K；e0为元电荷的电量，1.602×10-19C；ε0为真空介电常数，8.854×10-12F/m；εpore为膜孔内溶液的介电常数；εb为进料主体溶液的介电常数。

2 数学模型构建

2.1 高维模型表征

HDMR 方法将输出变量表示为一系列输入变量的函数之和，常用的带交互关系的简化表征多项式如式(13)所示[20]：

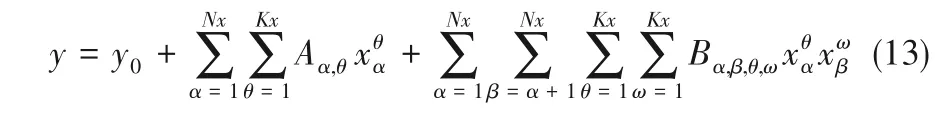
式中，y 代表输出变量；y0为常数；Aα,θ和Bα,β,θ,ω分别为多项式的一阶系数和二阶系数；Nx为输入变量x的个数；Kx为输入变量x的最高次数；上角标θ和ω表示输入变量x的次方数；下角标α和β表示输入变量x的类型。具体约束条件及目标如式(14)～式(15)：

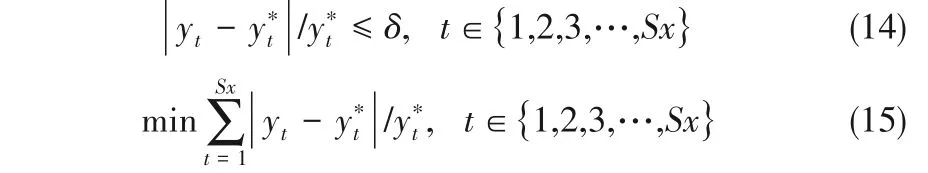
式中，yt和yt*分别为代理模型预测值和输出变量真实值；δ 为模型允许误差；Sx 为训练集的样本数量。

2.2 压力容器单元

将训练好的纳滤膜代理模型应用到压力容器的建模当中，一个压力容器通常由4～8 个标准螺旋卷式纳滤膜元件串联封装组成[21]，其结构如图1所示。

图1 纳滤膜压力容器结构示意图Fig.1 Structural diagram of the pressure vessel of nanofiltration

压力容器建模的关键是物料衡算，上一个膜元件出口处溶液的压力、浓度和流量是下一个膜元件的入口参数，因此需要对膜元件进行逐一计算，其衡算关系如下列方程组[式(16)～式(19)]所示[22]

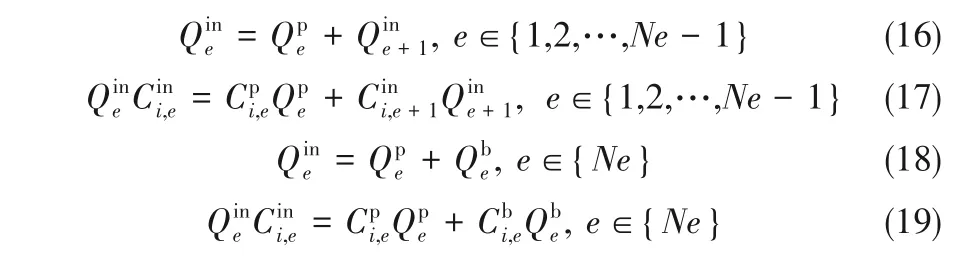
式中，Q和C分别为流量和浓度；Ne为单个压力容器内膜元件的个数；上角标in、p 和b 分别对应入口、透过液以及最后一个膜元件出口卤水的性质；下角标e 和e+1 表示膜元件在压力容器内排列的序号。

忽略盐通量对透过液体积的影响，则跨膜渗透水通量、单个膜元件的水回收率和盐离子截留率可分别用式(20)～式(22)表示：

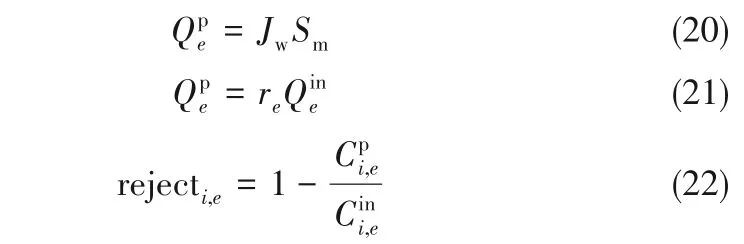
式中，Sm为单个膜元件的有效膜面积，m2；re为单个膜元件的水回收率；rejecti,e为单个膜元件对第i种离子的截留率。对于每个膜元件的渗透水通量，可用哈根-泊肃叶方程式来描述：

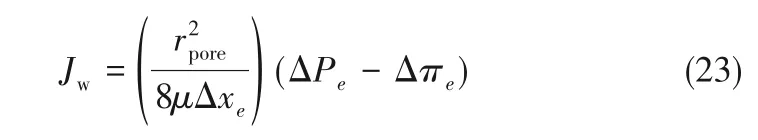
式中，μ 为溶液黏度，Pa·s；Δxe为膜有效活性层厚度，它是膜活性层厚度与孔隙率的比值；ΔPe为膜元件的操作压力。膜元件的跨膜渗透压差Δπe可通过范特霍夫方程进行计算

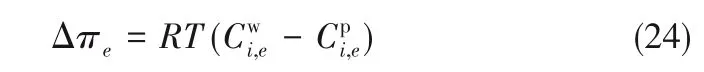
2.3 多级纳滤系统

多级纳滤系统模型如图2 所示，煤化工装置产生的含盐废水首先经过低压循环泵(circulating pump,CP)输送到预处理设备进行预处理过程，循环泵做功为：

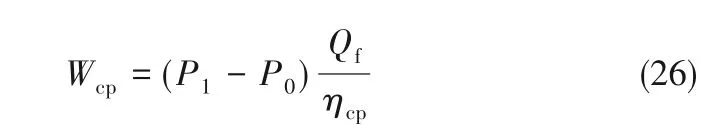
式中，P1为盐水在管道中的输送压力，通常为2～3 bar(1 bar = 0.1 MPa)[23]，本文取2 bar；P0为大气压，1.01325 bar；Qf为进料流量；η 为效率；下角标cp代表循环泵。

经过预处理的废水分成两股水流：一股与最后一级纳滤过程排出的高压浓盐水在压力交换机(energy recovery device,ERD)内进行换压，换压后的液体压力达到第一级纳滤所需的进料压力；另一股则直接通过高压泵(high pressure pump, HP)加压到指定的操作压力。此过程中压力交换机回收的能量和高压泵的能耗分别为[24-25]

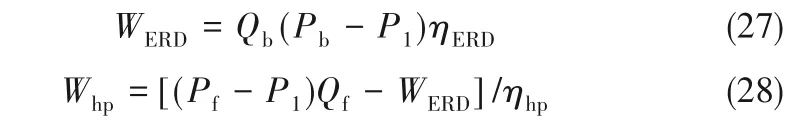
式中，Qb和Pb分别为最后一级纳滤装置出口处卤水的流量和压力；Pf为第一级纳滤装置入口处的操作压力；下角标，ERD 和hp 分别代表压力交换机和高压泵。

两股液体在混合阀混合后进入第一级纳滤装置进行分盐，上一级纳滤装置出口处的浓缩盐水经过中间加压泵(booster pump,BP)进一步加压输入到下一级纳滤装置中，加压泵所需要的功率为

多级纳滤系统的总能耗可通过式（30）计算：

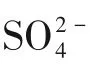
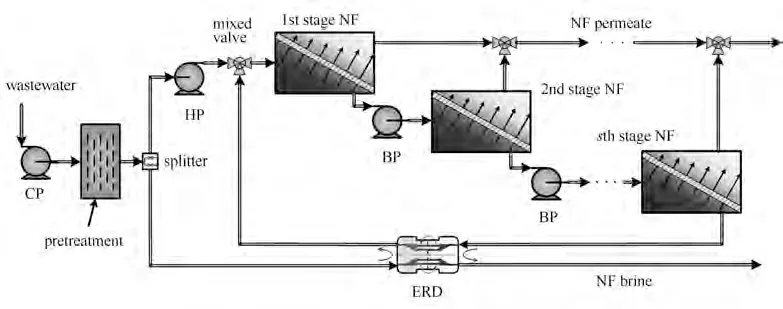
图2 多级纳滤过程示意图Fig.2 Flow diagram of multi-stage nanofiltration system

式中，MNaCl为NaCl 的相对分子质量，58.5；SEC单位为kW·h/kg(以每千克NaCl计)。而NaCl总回收率RR则定义为

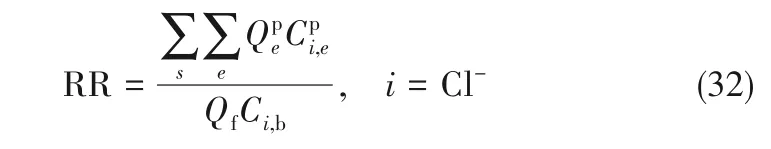
3 案例研究

本文所涉及的采样方案和多级纳滤过程模拟均在MATLAB R2015b 中完成。HDMR 模型训练和多级纳滤模型优化均借助于GAMS 24.4.6；其中，HDMR 模型训练所用求解器为CPLEX，多级纳滤模型优化所用求解器为CONOPT。

3.1 纳滤膜传质模拟

基于上述DSPM-DE 纳滤膜传质机理模型，本研究对煤化工含盐废水经过纳滤膜的传质过程进行模拟，预测透过液的离子浓度，并以此作为训练代理模型的样本数据。为简化计算，考虑煤化工含盐废水中只含有NaCl 和Na2SO4两种无机盐，且假设废水在循环运行过程中水温保持恒定。选用的纳滤膜为美国陶氏公司制造的NF270-30/440i(以下简称NF270)，主要相关参数列于表1。值得注意的是，纳滤膜表面的电荷密度Xd与进料溶液的离子浓度密切相关，通常由实验来确定[30]。通过对实验数据[12]进行线性拟合，推导得出NF270 纳滤膜电荷密度Xd与进料溶液离子强度I(mol/m3)的关系为Xd=-0.4808I-105.99，拟合精度r2=0.983。另外，由于纳滤膜传质过程中膜孔内溶液基本为NaCl溶液，孔内介电常数εpore的选取以NaCl溶液为基准。

3.2 样本生成与HDMR训练

参考典型煤化工废水的浓度[31]，本文中SO-浓度的变化范围为50～100 mol/m3，Cl-浓度的变化范围为150～250 mol/m3，Na+的浓度可根据电中性条件相应确定。在构建HDMR 过程中，选择进料液中三种离子(SO-、Cl-和Na+)的浓度以及跨膜渗透水通量(3.5×10-6～6.5×10-6m/s)为输入变量，分别设为x1，x2，x3，x4，以透过液中SO-和Cl-的浓度作为输出变量。每个输入变量变化区间内采用正交采样构建样本空间，包含1617个样本数据作为训练集，300个样本数据作为验证集。训练前需要对输入变量作归一化处理，使其映射到[1,2]范围内。本次训练输入变量的最高次数Kx=2，训练模型允许的最大相对误差为5%。

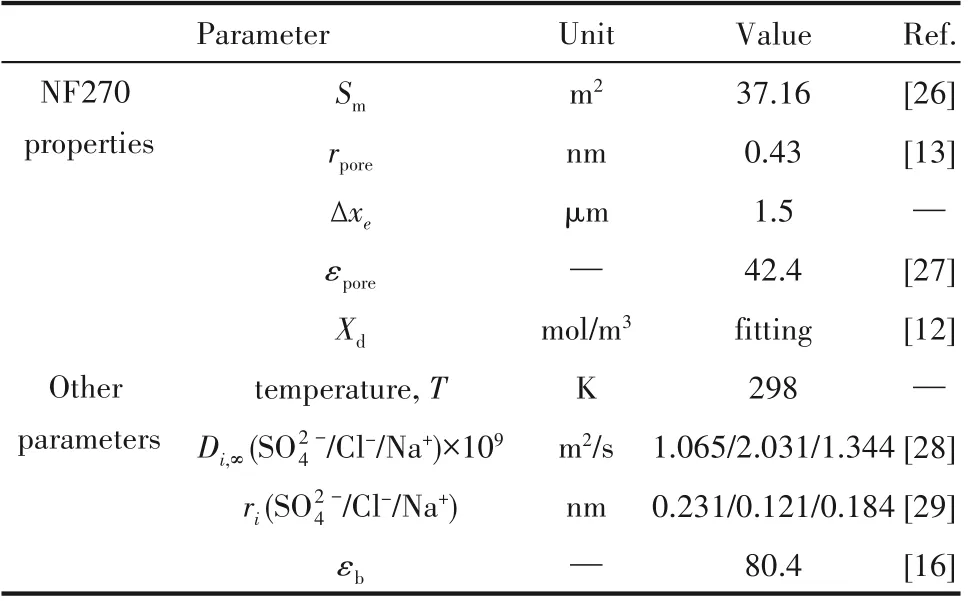
表1 纳滤传质模拟模型的关键参数Table 1 Key parameters of the mass transfer model for nanofiltration

3.3 优化模型

将训练后的多项式代理模型应用于优化过程，以最小化的分盐比能耗为优化目标，考察进料浓度变化(SO-浓度维持在50 mol/m3，Cl-浓度从150 mol/m3变化到200 mol/m3，相对应的进料离子浓度比[Cl-]/[SO-]变化范围为3.0～4.0)对多级纳滤系统性能和最优操作条件的影响。除代理模型本身的参数约束外，相关的参数值和约束值如表2 所示。基于表2 中的参数，各级的压力容器数量大致范围可通过对多级纳滤系统模型进行初步非线性优化得出。由于压力容器的数量为整数，考虑到多级纳滤系统需要在相同的膜元件数量下(总膜面积相同)比较才合理，因此根据陶氏公司提供的技术手册[22]，纳滤装置分别为单级、双级和三级时压力容器的数量选为75、50/25和32/23/20。

4 结果与讨论

4.1 纳滤膜传质机理模型验证

本节旨在将纳滤膜传质模型的模拟结果与陶氏商业软件ROSA运行结果进行对比验证，以ROSA结果为实验值，比较给定进料条件下不同水通量所对应的不同离子的截留率及进料压力，相关结果如图3 所示。计算得到的Cl-、Na+和SO-的截留率相对误差绝对值的平均值分别为3.77%、1.66%和1.53%，而进料压力相对误差绝对值的平均值为3.30%。此外分别对最低和最高临界浓度条件下的验证发现所得相对误差绝对值的平均值均小于15%，同时模拟所得Cl-的截留率区间与文献[32]以及陶氏官方网站[33]公布的范围(50%左右)接近。综上所述，在误差允许范围内可以认为，此纳滤膜传质模型在一定进料浓度范围内能够有效地模拟出煤化工含盐废水经单个纳滤膜元件处理后的透过液离子浓度，可以此作为高维模型表征的依据。

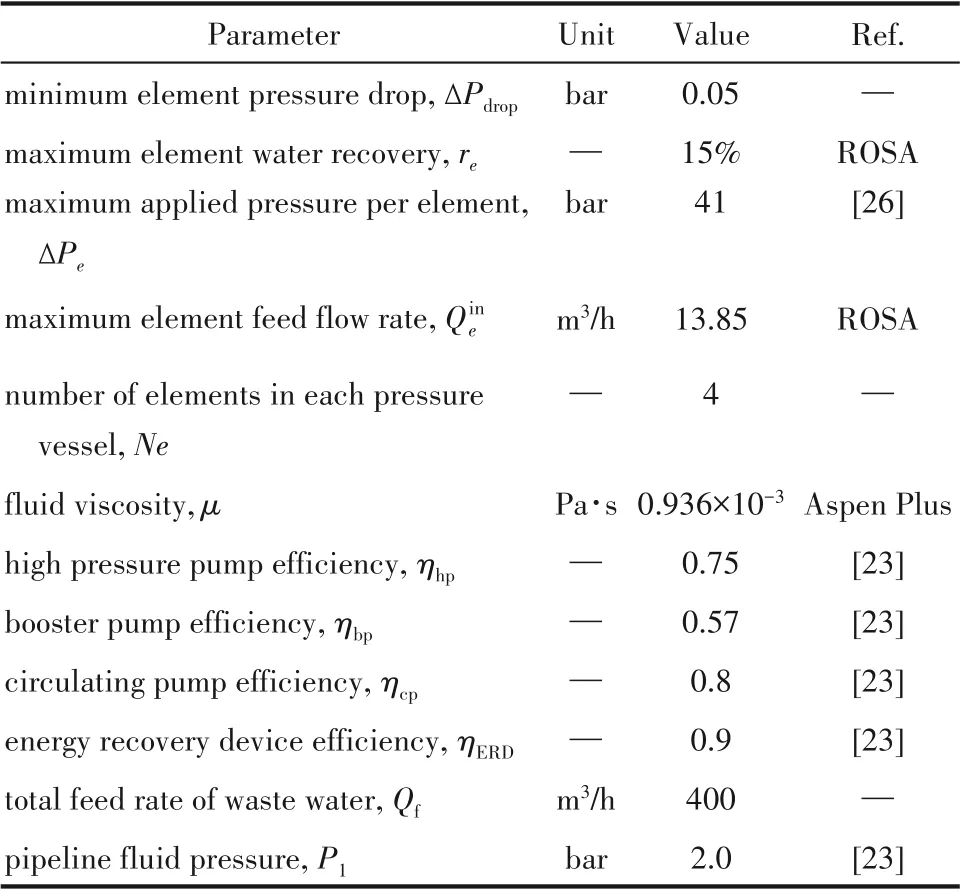
表2 优化模型的关键参数和约束条件Table 2 Key parameters and constraints used in optimization process

4.2 HDMR预测结果

4.3 多级纳滤系统优化结果

图5给出了不同级数下最优分盐比能耗随进料中[Cl-]/[SO-]变化的曲线。由图可知增大进料[Cl-]/[SO-]有利于降低分盐比能耗，下降趋势略有变缓，最高降幅可达27%。然而，随着进料[Cl-]/[SO-]的增大，双级系统和三级系统相对于单级系统的节能优势在减弱。例如，当[Cl-]/[SO-]=3.0和4.0时，二级系统较单级系统分别节能5.84%和3.53%，节能效果降低；而当[Cl-]/[SO-]＞3.9 时，三级系统和单级系统的最优分盐比能耗曲线已接近重合。尽管如此，在所研究的进料[Cl-]/[SO-]范围内，双级系统的最优分盐比能耗均是最低，与单级系统相比最高可节能5.84%。因此，在设备投资成本相同的前提下，双级系统配置是实际煤化工含盐废水分盐工艺中较为理想的选择。

图3 不同水通量下对应的DSPM-DE模型模拟值与实验值的比较(进料浓度：SO -80 mol/m3，Cl-180 mol/m3)Fig.3 Comparison of simulation data by DSPM-DE model and experiment data under various water fluxes(feed concentration:SO- 80 mol/m3,Cl-180 mol/m3)

表3 透过液SO - 浓度代理模型一阶系数Table 3 First order coefficients of surrogate model for SO - concentration in permeate

表3 透过液SO - 浓度代理模型一阶系数Table 3 First order coefficients of surrogate model for SO - concentration in permeate

ASO2-4 α,θ α=1 α=1 α=3 α=4 θ=1-0.014436-0.011062—-0.012763 θ=2 0.022249 0.002860—0.003062

表4 透过液SO- 浓度代理模型二阶系数Table 4 Second order coefficients of surrogate model for SO- concentration in permeate

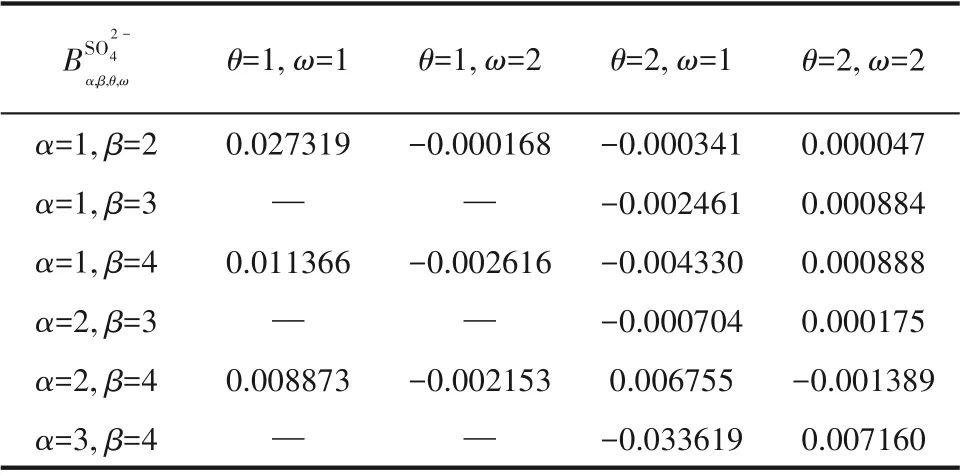
表4 透过液SO- 浓度代理模型二阶系数Table 4 Second order coefficients of surrogate model for SO- concentration in permeate

BSO2-θ=2,ω=2 0.000047 0.000884 0.000888 0.000175-0.001389 0.007160 4 α,β,θ,ω α=1,β=2 α=1,β=3 α=1,β=4 α=2,β=3 α=2,β=4 α=3,β=4 θ=1,ω=1 0.027319—0.011366—0.008873—θ=1,ω=2-0.000168—-0.002616—-0.002153—θ=2,ω=1-0.000341-0.002461-0.004330-0.000704 0.006755-0.033619

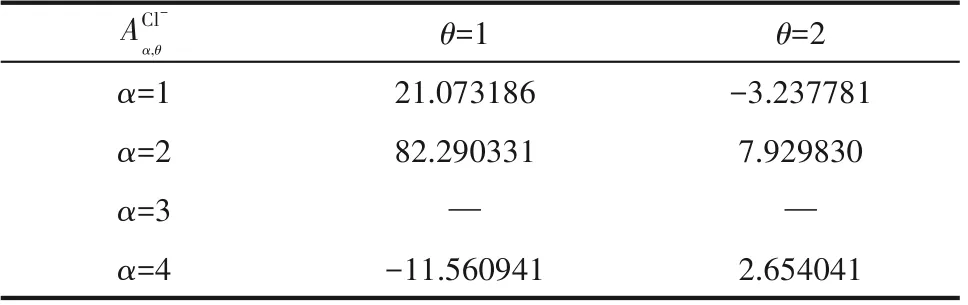
表5 透过液Cl-浓度代理模型一阶系数Table 5 First order coefficients of surrogate model for Cl-concentration in permeate

表6 透过液Cl-浓度代理模型二阶系数Table 6 Second order coefficients of surrogate model for Cl-concentration in permeate

比能耗的计算与总能耗和分离的NaCl 的质量密切相关，接下来从这两个方面深入讨论。首先总能耗主要来源泵的压力做功。图6为不同级数下各级单元的最优操作压力随进料[Cl-]/[SO-]变化的曲线。所有级单元的最优操作压力均随进料[Cl-]/[SO-]的增大而增加，且增幅随着级数的增大逐渐呈上升趋势，三级系统的最优操作压力上升最为明显。显然，双级系统中的第一级单元对应的操作压力最低，这与双级系统的最优分盐比能耗最低是密切相关的。值得注意的是，三级系统中的第一级单元的最优操作压力略高于第二级单元，通过查看优化结果数据发现它们之间的加压泵基本不做功，这是由于两级间的压降造成的。由于级数增加后，系统能耗的提高主要源于添加的级间加压泵，可见泵不做功对节能是有利的。有趣的是，加压泵不做功时前两级可以看作是整体，相当于从侧面说明双级系统的优越性。从整体上看，双级系统和三级系统的最优操作压力皆比单级系统的要低，平均降幅为6.4%。考虑到低压操作对于延长纳滤膜的使用寿命是具有积极意义的，故双级系统相对而言更好地满足低压操作的生产要求。

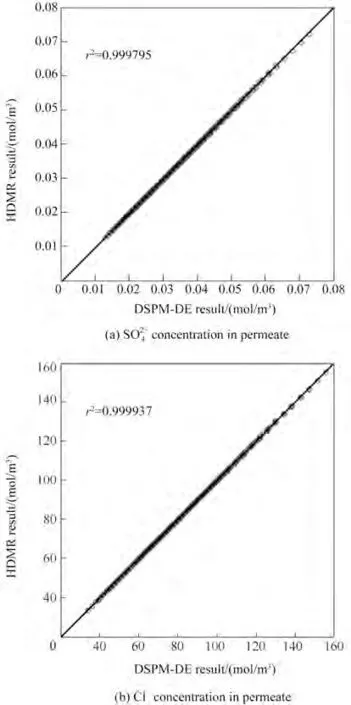
图4 HDMR预测值与DSPM-DE纳滤模型模拟值的比较Fig.4 Comparison of results obtained by HDMR and DSPM-DE models

图5 不同级数下最优分盐比能耗随[Cl-]/[SO - ]变化曲线Fig.5 The optimal SECs in different stage with varied[Cl-]/[SO- ]

图6 不同级数下各级单元的最优操作压力随[Cl-]/[SO - ]变化曲线Fig.6 The optimal unit operating pressures in different stage with varied[Cl-]/[SO - ](s1,s2,s3 represent the first,second and third unit of system)

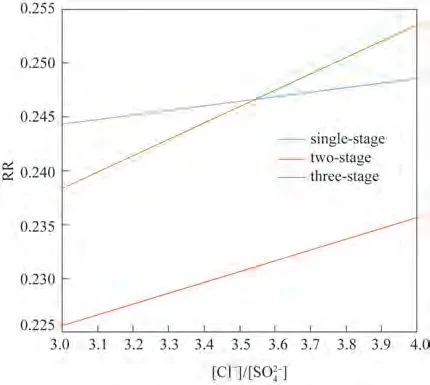
图7 不同级数下NaCl总回收率随[Cl-]/[SO- ]变化曲线Fig.7 The overall recovery of NaCl in different stage with varied[Cl2-]/[SO- ]

对于系统优化得到的NaCl总回收率，不同级数下其随着进料[Cl-]/[SO-]的变化趋势如图7 所示。从斜率可以看出，NaCl 总回收率的增幅随着系统级数的增加而增大，最高增幅可达6.43%。与先前得到的最优分盐比能耗曲线横向对比，发现级数变化时总能耗的变化幅度比NaCl 总回收率的变化幅度大，比如由单级系统变为双级系统时总能耗的降幅比NaCl总回收率的降幅大，因此才会出现双级系统比能耗最低的情况；而由双级系统变为三级系统总能耗的增幅比NaCl总回收率的增幅大，从而出现三级系统比能耗高于双级的情况。而当进料[Cl-]/[SO-]＞3.5 时，三级系统的NaCl 总回收率超过单级系统的，但两者最优分盐比能耗差距却在逐步缩小，这再一次印证了第二条小结论。综合上述分析，实际生产过程需要在总能耗和NaCl总回收率两者之间寻求均衡，这正是双级系统的优势。

5 结 论

本文将DSPM-DE 模型引入到煤化工含盐废水的纳滤传质模拟中，并在此基础上通过HDMR 的方法建立纳滤膜的代理模型，将其耦合在多级纳滤系统优化模型建模过程中。通过实际案例数据研究了进料液中[Cl-]/[SO-]变化对不同级数纳滤系统的最优性能和操作条件的影响。优化结果表明，增大进料[Cl-]/[SO-]有利于提高NaCl 总回收率，最高增幅可达6.43%，同时有利于降低分盐比能耗，最高降幅可达27%。在膜投资成本相同的情况下，双级系统在实际生产中占有节能优势，与单级系统相比最高可节能5.84%。