微波化学反应的无量纲准数动力学模型研究：以偶氮二异丁脒盐酸盐（AIBA）分解反应为例

毛桃嫣，邹敏婷，郑成，2，曾昭文，伍旭贤，肖润辉，彭思玉

（1 广州大学精细化工研究所，广东广州510006； 2 岭南师范学院，广东湛江524037）

引 言

微波辐射技术凭借降低能耗、减少生产成本的优势，已广泛应用于各个领域[1-6]。尤其是在化学合成方面，选择性高、速率快等优点，是一个绿色高效的物质转化过程[7-10]。国内外许多学者对微波化学反应动力学进行了研究[11-14]，但大部分局限于单一因素对反应速率的影响。而多项研究表明，微波对于化学反应的作用是一个多因素共同作用的复杂过程。动能的影响因素有密度、黏度、压力和流速[15-18]；微波热能部分考虑的因素一般有温度、比热容、热导率和加热物质的密度[15-20]；微波电磁的影响因素主要有微波频率、功率密度和加热物质的介电性质[15-18,21-25]。因此只考察单一因素对微波反应动力学的影响难以进行过程放大设计及工业化应用。

近年来，为了推进微波辐射技术工业化进程，学者们逐步开始建立微波辐射下的化学反应多因素动力学模型，并且获得了相应的学术成果。汤建伟等[26-27]在液相反应物浓度、固体颗粒直径和密度等因素不变的情况下，将指前因子A视为常数，根据各微波功率下的实验数据分别通过线性拟合得到包含有频率因子(指前因子)的参数A 和反应活化能E 的数值，最终建立了磷矿分解微波非等温过程的反应动力学方程。杨晓庆[28]利用时域有限差分方法联合求解了化学反应方程、Maxwell方程和热传导方程，得到化学反应体系的动力学参数，为微波反应的建立提供了理论基础。Sturm 等[15]通过建立电磁模型、传热模型、流体力学模型，研究温度在时间和空间上的分布和变化。Patil 等[16]分别从电磁、传热和流动三个方面对微波在连续流反应器中的加热过程进行了模拟。Zhu 等[17]也建立了液体连续流的电磁场、能量和动量三个数学模型。Wu等[18]结合麦克斯韦方程、热传导方程、反应动力学方程和纳维-斯托克斯方程建立了乙酸乙酯连续流动过程模型。但这些模型研究的还是动能、热能、电磁场等单个方面的模型，并没有把各种影响因素结合起来，因此依然很难达到工业化预测的效果。

同时要科学讨论研究微波反应动力学模型，必须精确控制实验的条件（如温度、压力、功率等），特别是微波功率。一般地，微波加热装置采用温控加热模式，一旦加热达到设定的温度，微波辐射的输出功率就会降低，此种情况下建立的微波反应模型误差大。本课题组[29]在2009 年进行的一组实验的过程中发现，如果设置的微波反应温度低于反应溶剂的沸点时，微波一直处于间歇工作状态，并不能完全体现出微波的作用，为此本课题组设计了沸腾回流的方法，实现了微波的持续作用，并在不同的复合溶剂体系中进行化学反应的动力学研究。Dudley 等[30-31]也在回流状态下研究了两种加热方式的反应动力学，发现稳态微波辐射加热下的反应速率更快，指出微波功率是实现所需反应活性的一个重要因素。

本文通过选择合适的溶剂调整其复配比例，得到一系列具有不同沸点的混合溶剂作为反应介质，使反应在混合溶剂沸点下进行，以保证反应过程中温度的一致性和微波的持续不间断作用来研究微波反应。从微波作用下动量传递、热量传递和质量传递的影响因素进行较为全面的考虑，基于量纲分析方法中的参数必要和充分，选择了微波功率密度p、黏度μ、密度ρ、反应物的浓度CA、温度T、热导率l、体系的损耗角正切tanδ 和微波辐射频率f 作为考虑因素建立一个微波辅助有机反应动力学模型，解决微波反应过程放大的基础性问题，有望用于指导微波反应工程的工业化。

1 实验部分

1.1 实验原料

偶氮二异丁脒盐酸盐（AIBA）是由上海阿拉丁生化科技股份有限公司生产，纯度为97%,密度为0.42 g·ml-1(20℃)，沸点为267℃（101.325 kPa）。无水乙醇是由天津市致远化学试剂有限公司生产，分析纯，密 度 为0.789 g·ml-1（20℃），沸 点 为78.5℃（101.325 kPa）。沸石是由天津市致远化学试剂有限公司生产，孔径0.250～0.425 mm。所有试剂均未进行提纯就直接使用。纯水是由超滤纯水机制备。

1.2 实验方法

AIBA分解反应是一个经典有机化学反应，在加热的过程中，反应体系会释放出N2。本文在微波加热方式下研究AIBA 的分解反应动力学过程。AIBA分解过程示意图如图1所示。

图1 AIBA分解反应过程示意图Fig.1 Schematic diagram of AIBA decomposition reaction

微波加热实验方法：称取2.170 g(8 mmol)的AIBA于特制的250 ml玻璃反应器中（玻璃不吸收微波辐射），加入一系列不同复配比例的60 ml 水-乙醇混合溶液作为溶剂，搅拌至AIBA 溶解，得到无色透明的溶液。将适量的沸石加入到反应瓶中，防止因加热而出现的暴沸现象。并将反应瓶置于微波反应器（CEM MARS 6）中，反应瓶与冷凝管之间用玻璃延长管进行连接。所有操作均在大气压下进行，在加热过程中，采用微波持续不间断的恒温加热模式，同时通过冷凝以达到强回流的效果，反应瓶内的温度采用光纤温度传感器监控。每间隔5 min 取出少量的待测溶液，并迅速冷却到室温，以使反应能够完全停止。利用紫外-可见光分光光度仪分析在367 nm处的吸光度[32]。

1.3 微波反应装置

在本研究中，使用的是多模微波反应器（CEMMARS 6），规格为：腔容积，0.066 m3；微波频率，2.45 GHz；允许最大微波功率，1800 W，允许最高温度：300℃；MARS 连续非脉冲功率输出；温压控制；自动电磁搅拌。为了精确测量温度，微波配备了光纤温度传感器，能精确测定反应体系内部温度，实验装置图见图2。

2 动力学模型的建立

量纲分析法是一种建立在实验基础上的工程实验研究方法，在解决化学工程问题上有着至关重要的指导作用。该法可以正确地分析过程中各个物理现象变量之间的关系，进而建立简明的数学关联式，可以大大地减少工作量和实验次数，且模型结果便于推广和应用[33-34]。

任意一个物理问题、物理现象或者物理关系涉及到n 个物理量（P1,P2,P3,…,Pn），物理量之间存在的数学关系如式（1）所示。其中基本量纲数量为m，则由此可以组成n-m 个独立的无因次数群，定义为Π1、Π2、Π3、…、Πn-m，由式（1）可转换成无量纲的形式，无因次数群之间的函数关系[33-34]见式（2）。

如图3 所示，利用量纲分析法建立数学模型,并通过实验研究确定关系式的无量纲因子[35]。但是通过量纲分析法得到的结果是半定量化的，其中数学关联式中也会存在未知的常数[33,36]，这些未知的常数可以通过实验或理论的拟合进一步确定。

图3 量纲分析建模流程Fig.3 Dimensional analysis modeling process

微波辐射可以对化学反应体系进行加热，是微波与反应体系中的极性分子相互作用的结果。但微波对于化学反应的作用是一个复杂的过程，经分析，选取微波功率密度p、黏度μ、密度ρ、反应物的浓度CA、温度T、热导率λ、损耗角正切tanδ和微波辐射频率f 作为影响因素，通过量纲分析法对微波反应进行初步了解与分析，为微波化学反应提供理论支撑。

3 实验结果与分析

3.1 在微波加热方式下的实验结果

图4 AIBA分解反应在微波辐射下的加热曲线和功率曲线Fig.4 Heating and power curve of AIBA decomposition reaction under different microwave irradiation

3.1.1 微波加热方式下的温度与功率 图4展示了在反应过程中利用光纤温度传感器记录反应过程的加热曲线以及微波加热装置记录的功率曲线。结果表明，实验过程成功地实现了恒温、微波连续不间断辐射的条件，与预期实验条件相符。

3.1.2 微波实验结果与分析 本文通过测定在微波加热下，一定时间内反应物AIBA 浓度的变化值来进行反应动力学模型的研究。通过复配一系列无水乙醇-水溶液（体积比分别为1.5∶8.5、2∶8、2.5∶7.5、3∶7、3.5∶6.5），得到一系列不同沸点温度的溶液。在不同的微波功率（500、400、300、200 W）下进行反应，每隔5 min 测定利用紫外分光光度计测定反应物AIBA 浓度CA，微波加热方式下的动力学结果见图5。

3.2 微波动力学模型

3.2.1 模型的假设

（1）微波频率固定在2.45 GHz。

（2）液体混合物是均匀的单相溶液。

（3）取样检测体积忽略不计，各组分在反应器中均匀分布。

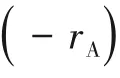
式中，热导率、黏度和密度是通过摩尔平均原理得到的[式（4）～式（6）]，其中xi代表i 组分的摩尔分数，μi、ρi和λi分别代表i 组分的纯物质的热导率、黏度和密度，由于反应物含量少，因此本文只考虑两种混合溶剂的混合热导率、黏度和密度。

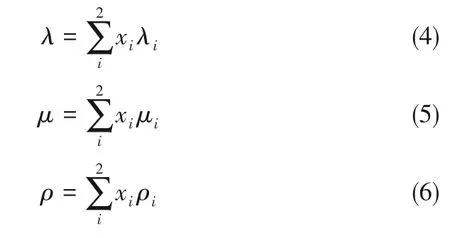
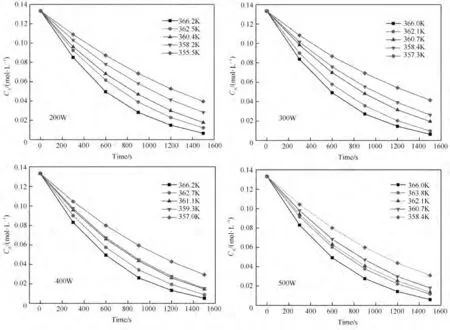
图5 AIBA在微波加热的浓度变化曲线Fig.5 Variation curve of AIBA concentration under microwave heating

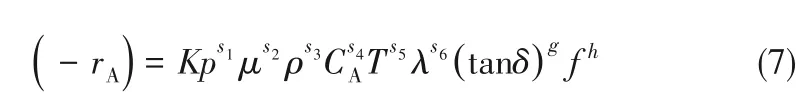
式中，K 为描述数学模型的物理常数。表1 的物理参数中，基本量纲有物质的量N、长度L、时间T、质量M、温度。根据Π定理，也称作相似特征数方程，组成无量纲的量的数量为具有量纲的物理参数与基本量纲数量之差，定义为Π1、Π2、Π3、Π4，无量纲的量之间存在着一定的函数关系，可以等价地表达成相应的无量纲形式，如下：

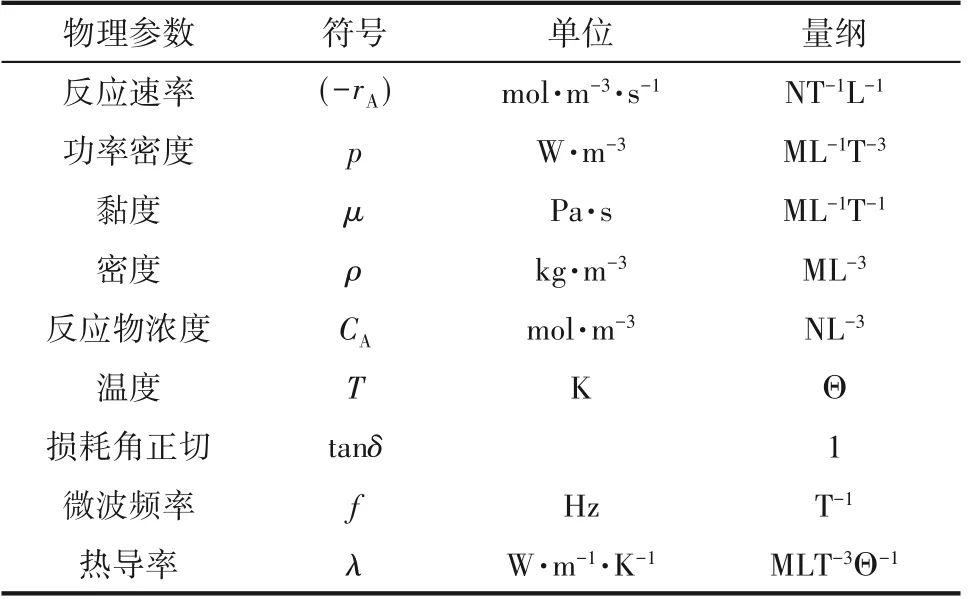
表1 物理参数的量纲Table 1 Dimension of various parameters

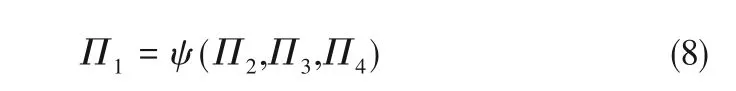
模型涉及的五个基本量纲分别为N、T、L、M、Θ，则可在9个物理量中选择5个具有独立量纲的物理量作为一组基本量去度量其余的物理量。选择p、μ、ρ、CA、tanδ、λ 为共同物理量，计算推导过程如式（9）～式（12）：

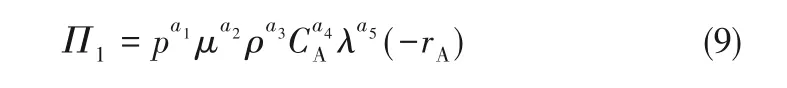
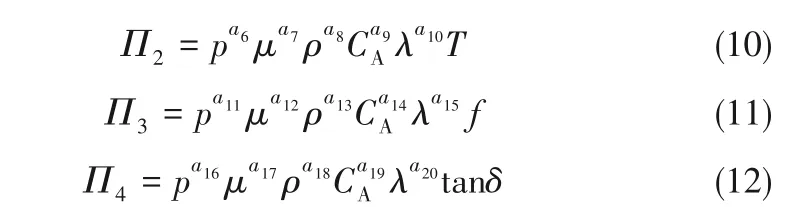
对于等式（9）而言，等式两端遵循量纲一致性的原则，通过推导可得到Π1的表达式，具体的表达式为式（13）：

同理，根据量纲一致性的原则，可推导Π2和Π3的表达式[式(14)～式(16)]：

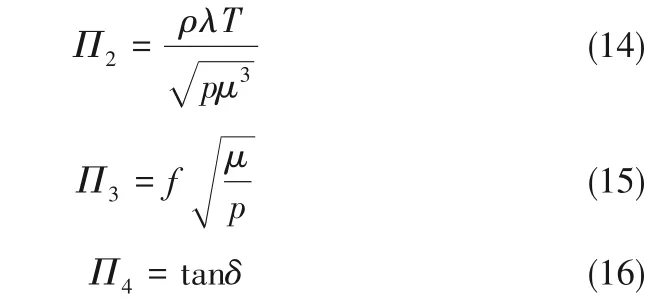
式（8）可转换成指数形式。指数形式的等式如下[式(17)～式(18)]：

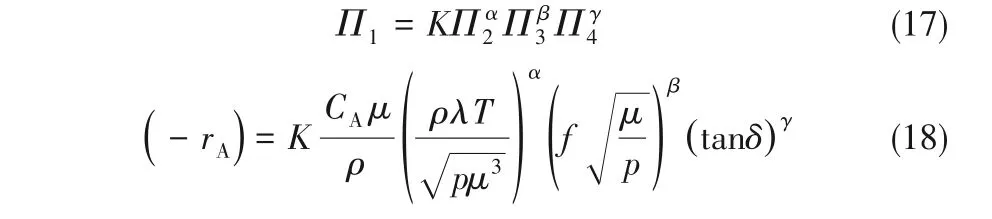
建立动力学模型过程中多使用实验数据（部分）如表2所示。

3.2.3 模型的性能评价 本文对模型进行非线性拟合，得出的模型参数结果为：K = 0.0005，α =2.4178，β = -2.3428，γ = 0.7573,分别反映了化学反应与质量传递、热量传递和动量传递对AIBA 化学反应速率的影响。采用平均相对误差（MRE）、平均绝对误差（MAE）、均方根误差（RMSE）指标对模型进行了评估，计算公式见式（17）～式（19），结果表明,MRE = 0.197， MAE = 1.043× 10-5， RMSE =1.450 × 10-5。

图6 的结果表明，模型估算值与实验值偏差较小，模型的相关度较高。可见，在误差范围内，该模型具有良好的预测能力。

4 结 论

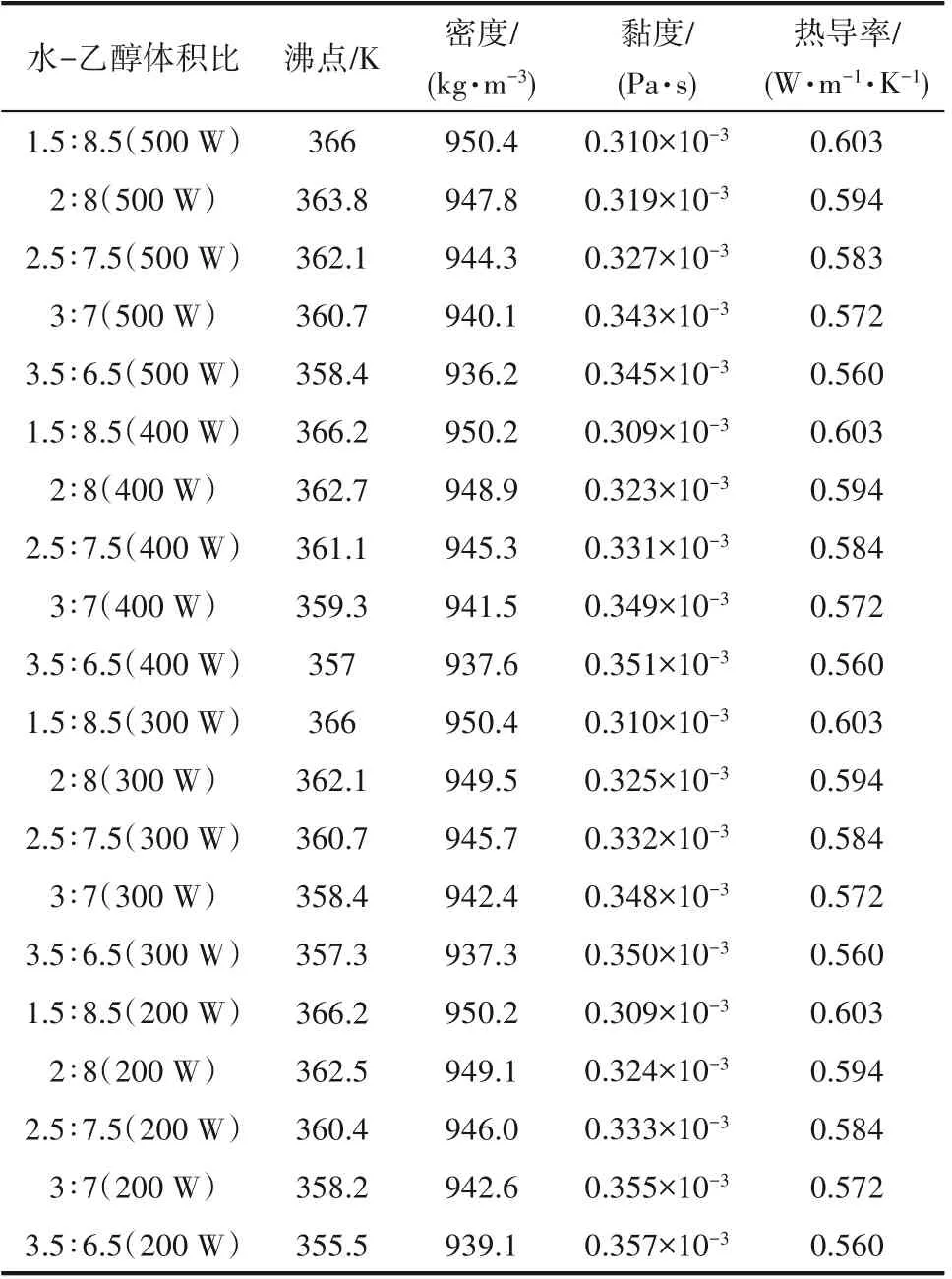
表2 不同复配比例下溶液的理化性质Table 2 Physical and chemical properties of solutions with different compound proportions

图6 实验值与估算值的比较Fig.6 Comparison between experimental value and estimated value