基于随机森林回归的围岩应力插值方法

王苏健，贾澎涛，金声尧

(1.陕西煤业化工技术研究院有限责任公司，陕西 西安 710100；2.西安科技大学 计算机科学与技术学院，陕西 西安 710054)

0 引 言

随着我国矿井开采深度的增加，因围岩应力增高而造成的事故时有发生，严重威胁着煤矿生产安全[1]。为了有效控制围岩应力，需要采取必要的监测预警手段，实现对矿井巷道和采掘工作面的实时监控预警[2-4]。在围岩应力安全监测中，采集数据的准确与否对矿山安全预警结果有着至关重要的影响[5]。但是在监测数据采集过程中，由于受井下恶劣的现场环境、设备和线路故障、人为因素等条件限制，采集到的围岩应力数据经常会存在缺失值的情况，严重影响了后续的数据分析、安全预警等工作。因此，对围岩应力监测数据的缺失值进行有效插补是亟待解决的问题[6-7]。

围岩应力监测数据是典型的时间序列数据，可以采用时间序列数据插值方法进行插补。常用的时间序列插值方法有传统的数理统计方法和机器学习方法。传统的数理统计方法有均值插值、中值插值、线性插值、最邻近插值、拉格朗日插值、样条插值等[8]。基于机器学习的插值方法有基于聚类的插值[9-10]、基于回归分析的插值[11]、基于神经网络的插值[12-14]、基于集成学习的插值方法[15]等。

在围岩应力数据插值领域，陆振裕等采用线性插值法，对于钻屑法获得围岩压力系列离散点数据进行插值，为后期冲击地压危险预测提供了有效的数据[16]。李凯拓同样采用线性插值法，对王庄煤矿三维地应力分量做了平滑处理，最终绘制出了各应力量分布云图[17]。宋道柱等采用等值线插值对单体液压支柱压力的误差数据进行修正，采用双线性内插法对缺失值数据进行插值，为支撑受力变化趋势分析提供有效数据[18]。尹时雨采用3次样条插值以及高阶多元非线性回归方程，对工作面各支架测点工作阻力数据进行插值拟合，为研究矿山压力显现规律提供理论依据[19]。徐恩虎等提出了一种连续插值模型，可以得到等步长与非等步长数例的任意内插值与外插值[20]。陈辉等提出了一种基于粒子群的3次样条插值算法，取得了比最邻近插值、拉格朗日插值、线性插值方法更好的插值效果[21]。冯俊军等采用克里金插值法得到的应力云图能够反映试验工作面巷帮煤体应力场分布规律，为巷道超前支护、顶板稳定性控制、围岩稳定性分析、冲击地压预防等提供理论依据[22]。

综合来看，以上学者多采用的是改进的传统插值方法，对基于机器学习的插值方法在围岩应力数据领域的研究还较少。

由于围岩应力数据缺失问题可以看作预测问题，用缺失值之前的数据预测缺失位置的数据，从而实现插值。因此，文中尝试采用机器学习中有监督集成学习方法——随机森林回归方法(random forest regression，RFR)，进行缺失数据的补全处理。首先，在集成学习理论的基础上，提出基于随机森林回归的围岩应力插值方法(interpolation based on random forest regression，IRFR)。然后，以无缺失的围岩应力时间序列数据为样本集，构建不同缺失情况的数据集，作为实验用数据。最后，在不同缺失值情况下，研究不同插值方法对不同缺失情况的围岩应力数据的影响，并就其插值效果进行比较分析。实验结果验证了IRFR的正确性与有效性。

1 基于随机森林回归的围岩应力数据补全

随机森林算法是由Brieman于2001年提出的一种集成学习算法[23]，用于解决高维非线性数据的分类预测、回归预测与特征选择问题。随机森林回归预测算法是bagging算法的改进算法，它用K个分类回归决策树(classification and regression tree，CART)作为基学习器[24]，以K个基学习器预测值的平均值作为最终结果。

基于随机森林回归方法的围岩应力插值方法(IRFR)的思路是输入围岩应力监测数据，用当前缺失值之前的指定窗口长度的历史数据训练随机森林回归模型，并输出预测值，该预测值就为插值的结果。如果是连续缺失的情况，采用递推方法进行预测补全。

1.1 围岩应力回归决策树

随机森林回归预测算法的基础是回归决策树CART算法。下面介绍围岩应力回归决策树建模过程。

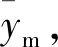
(1)

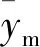
(2)

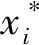
(3)

(4)

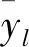
按照上述分割方法，分别将Rl和Rr作为父节点，递归进行分割，直至当前父节点中样本的y值方差小于给定方差阈值。条件满足时，停止递归并将当前父节点设置为叶子节点。至此，单棵围岩应力CART树就建立起来了。

1.2 IRFR模型构建

CART决策树能在一定程度上有效表示原始训练样本中的潜在统计关系，但往往较为粗糙，且不稳定。因此，应用集成学习的思想，在单棵CART树的基础上，构建基于随机森林回归方法的围岩应力插值模型——IRFR模型，则可有效弥补单棵CART树的不足。IRFR模型结构如图1所示。

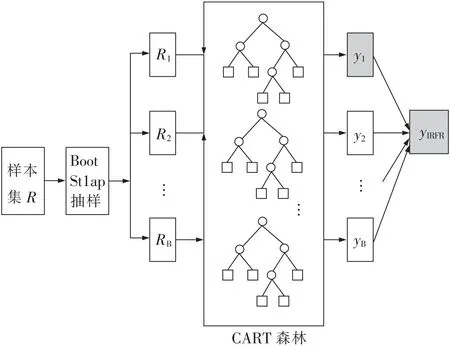
图1 IRFR模型结构Fig.1 Structure diagram of IRFR model

从图1可以看出，IRFR模型构建步骤如下

步骤1：采用Bootstrap抽样技术，从原始样本集R中有放回的抽取B个样本集，构建B个CART树进行学习训练，剩余未被抽取的样本作为袋外(out of bag，OOB)数据，形成模型的测试样本数据。

步骤2：设原始数据集变量个数为p，在每棵决策树模型的内部节点随机抽取k(k≤p)个变量作为备选分枝变量，按照单棵决策树构建过程寻找最佳分枝。

步骤3：每棵决策树自顶向下递归分枝，直至当前父节点中样本的y值方差小于给定方差阈值。条件满足时，停止递归并将当前父节点设置为叶子节点。

步骤4：根据数据的属性特征，生成的B棵决策树按照以下规则生成IRFR预测模型

yIRFR=ave(y(X,Tb)),b=1,2,…,B

(5)

式中Tb为第b棵回归树；y(X,Tb)为第b棵回归树的预测值。yIRFR的预测值是B棵树预测值的平均值。

2 实验数据与实验设计

2.1 实验数据

在某煤矿综采工作面进行围岩应力数据采样，从2019年5月7日10：00开始至2019年11月6日7：30分结束。按照采样间隔10 min，应采样26 338个数据，实际采样14 306个数据，缺失12 032个数据，缺失情况较为严重。连续缺失数据的频度情况如图2所示。

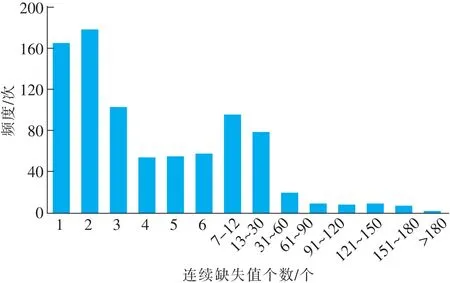
图2 数据缺失频度情况分布Fig.2 Distribution of data missing frequency

从图2可以看出，数据连续缺失1～30个的情况较多，连续缺失30个值以上的情况较少，连续缺失180个以上的情况只有2次。因此，为了方便实验，按照数据缺失的分布情况，把原始数据的缺失情况归纳为8种情况，这8种情况涵盖了大多数的数据缺失情况。

1)连续缺失值1～6个，对应缺失值较少的情况。

2)连续缺失值12个(2个小时)；

3)连续缺失值30个(5个小时)。

4)连续缺失值60个(10个小时)。

5)连续缺失值90个(15个小时)。

6)连续缺失值120个(20个小时)。

7)连续缺失值150个(25个小时)。

8)连续缺失值180个(30个小时)。

为了验证模型效果，选取无缺失值的一段序列，即2019年7月8日00：00至2019年7月19日23：50的1 728个围岩应力传感数据，作为实验数据。实验数据均值为24.317 7 MPa，标准差为6.508 4 MPa，最小值0.4 MPa，最大值45.8 MPa。按照以上8种缺失值情况，人为设置其缺失值，便于后续实验比较。

2.2 数据预处理

对实验数据集做归一化处理，将数值规范化到[0，1]之间。设围岩应力时间序列为R={x1,x2,…,xn}，标准化公式见式(6)。

(6)

式中i=1，2，…，n。归一化后的数据如图3所示。

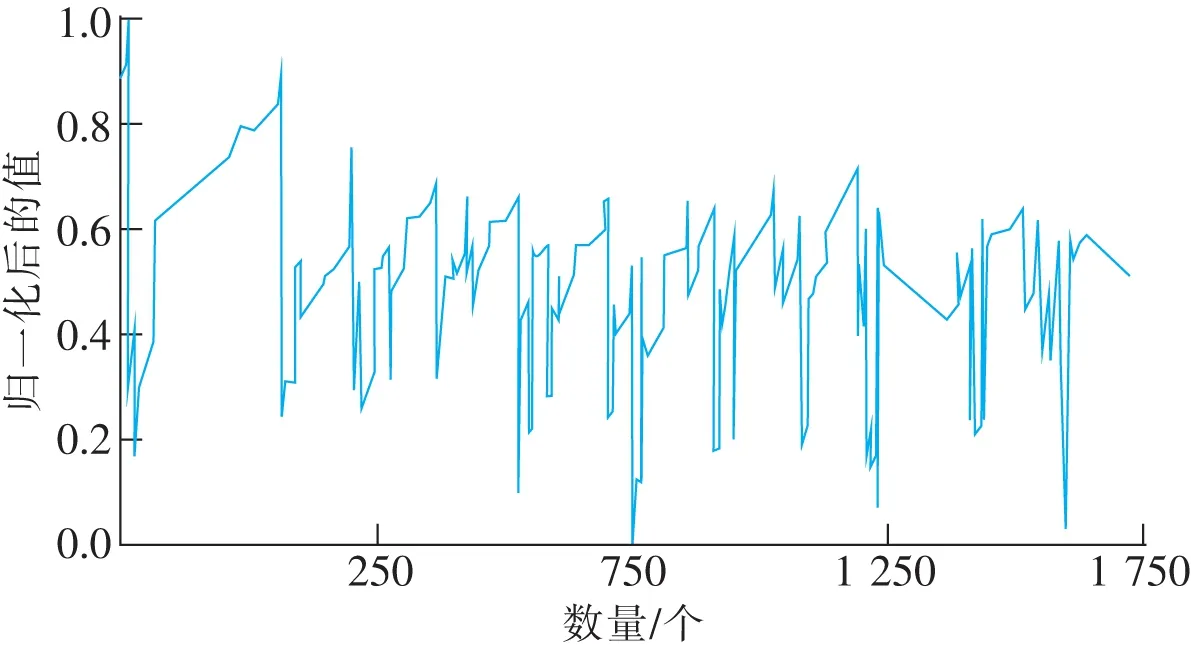
图3 实验数据Fig.3 Experimental data

2.3 对比插值方法

选择均值插值、中值插值、线性插值、最邻近插值(简称最邻近)、Zero阶梯插值(简称Zero)、3次B样条插值(简称Cube)、拉格朗日3次多项式插值(简称Lagrange)7种插值方法作为实验对比插值方法。这些插值方法均为较常用的插值方法，这里对其原理不再赘述。

2.4 IRFR参数确定

针对不同的数据缺失情况，IRFR模型需确定预测步长L、训练窗口长度n和决策树棵树B。

预测步长L设定为缺失数据个数；训练窗口的长度n一般由经验给出，这里设定为2倍的最大缺失值个数，即360。

IRFR模型中，决策树的棵数对预测结果的准确率和性能有较大的影响。因此针对某种缺失情况，通过比较不同决策树棵树下训练集的均方误差(mean square error，MSE)，从而确定决策树的棵数。

设围岩应力时间序列为R={x1,x2,…,xn,xn+1,…,xn+s}，某一时刻围岩应力的真实值为xi，拟合的插值为yi，预测步长为s，则预测值和真实值的MSE公式如式(7)所示。

(7)

设E={e1,e2,…,eB}为决策树棵树为1，2，…，B时的MSE误差，相邻误差的差值δ定义为

δ=ei+1-ei(i=1,2,…,B-1)

(8)

式中ε为预先给定的精度值。当δ<ε(ε>0)时，B为所求的最优棵数。

以缺失值为120个的情况为例，不同棵数决策树情况下的MSE如图4所示。从图4可以看出，随着决策树数量的增多，误差呈下降趋势。在棵树为500时，相邻误差差值小于指定的ε=0.000 1，因此选择决策树棵树为500。

2.5 实验结果评价

采用均方误差(MSE)作为评价指标，对不同插值方法的结果进行比较。

3 结果分析

采用IRFR方法和2.3小节中的对比插值方法，在8种缺失值情况(2.1小节罗列)的数据集上进行试验，将拟合值和真实值进行对比。

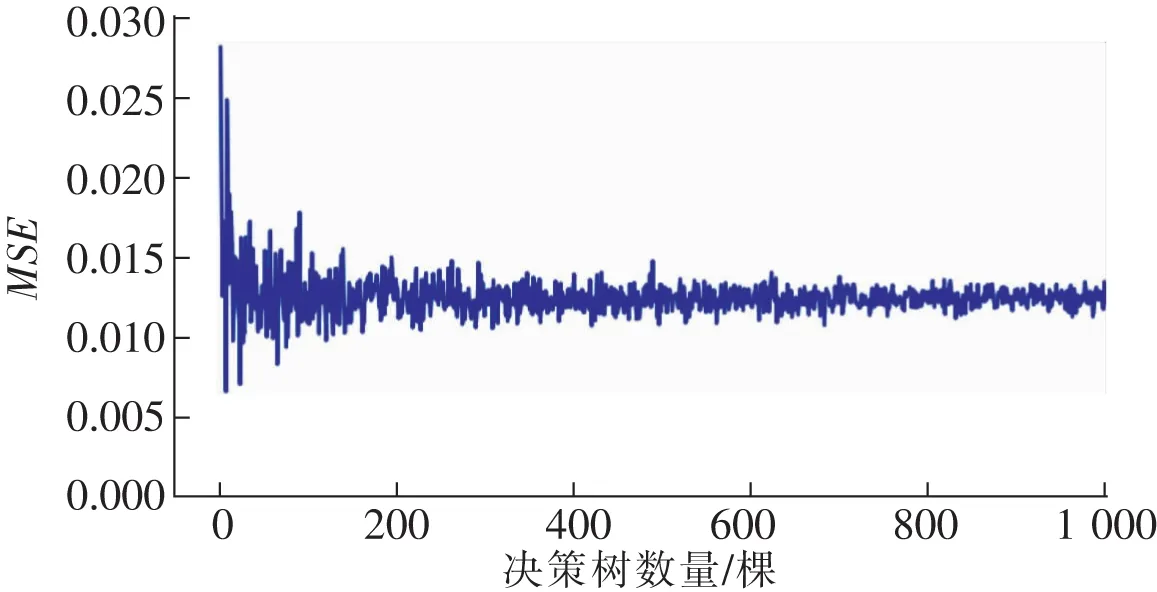
图4 不同决策树数量情况下的MSE误差Fig.4 MSE errors of different number decision trees

3.1 缺失值较少的情况

针对缺失值较少的情况(1～6个)，各插值方法的误差比较见表1(误差值取小数点后4位)。限于篇幅，仅列出连续缺失6个值的插值效果图，如图5所示(均值插值和中值插值效果较差，未显示)。

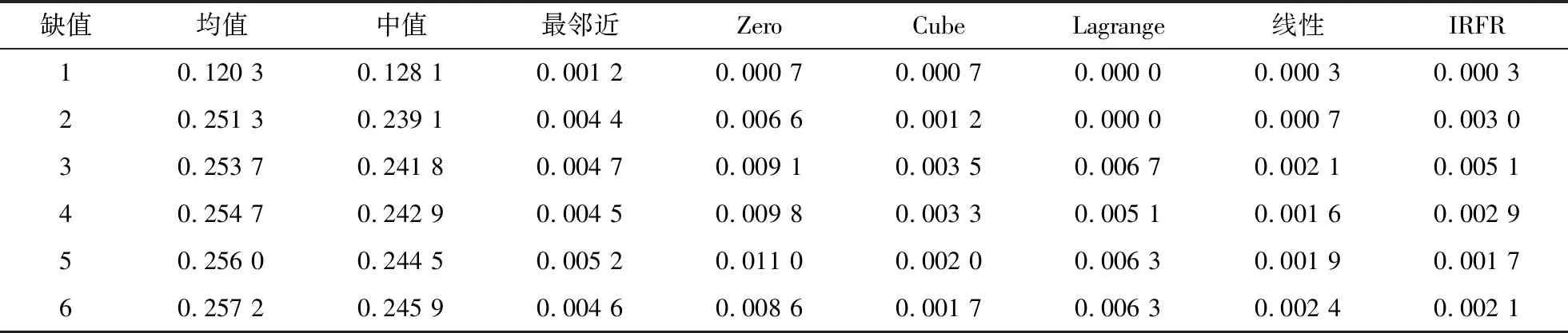
表1 缺失值较少情况下不同插值方法的误差比较Table 1 Errors comparison of different interpolation methods with fewer missing values

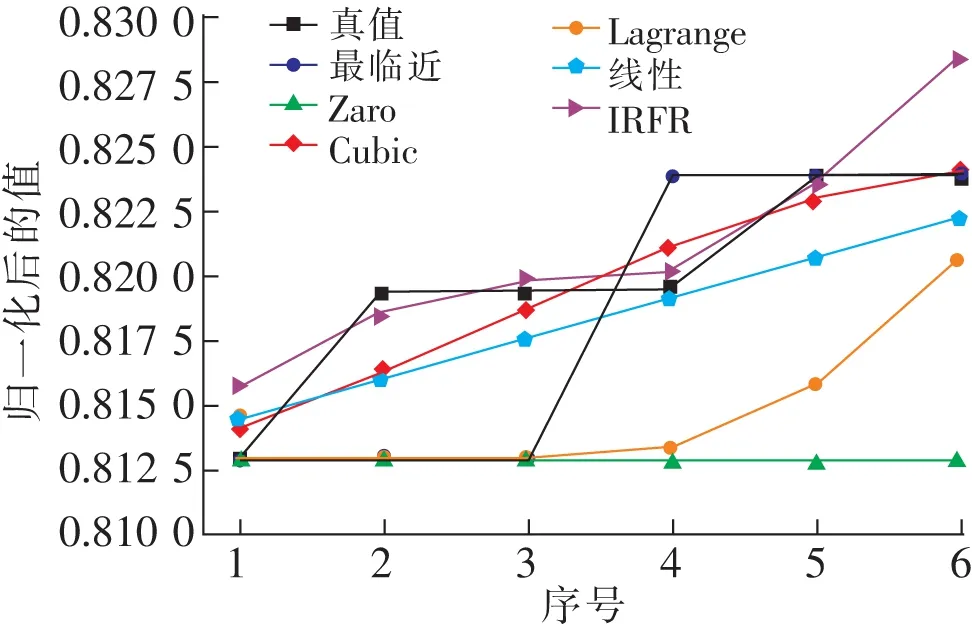
图5 连续缺失6个值情况下的插值效果对比Fig.5 Comparison of interpolation effects in the case of continuous missing 6 values

从表1可以看出，均值插值和中值插值效果较差；拉格朗日插值在连续缺失值1个和2个的情况下取得了最好的插值效果；线性插值在连续缺失值3～4个情况下取得了最好的插值效果；IRFR在连续缺失值5个情况下取得了最好的插值效果；从表1和图5可以看出，在连续缺失6个值情况下，Cube方法取得了最好的插值效果，IRFR次之。因此，在连续缺失值较少的情况下，线性插值、最邻近插值、Zero阶梯插值、3次B样条插值、拉格朗日插值和IRFR插值效果相当。

3.2 缺失值较多的情况

针对缺失值较多的情况(连续缺失值个数为12、30、60、90、120、150和180)，各插值方法的插值效果见表2(误差值取小数点后4位)。限于篇幅，此处只展示连续缺失12个值、30个值和180个值的插值效果图，如图6、图7、图8所示(图7、图8中，因为Lagrange插值效果太差，未显示)。

从表1和表2可以看出，均值插值、中值插值在缺失值较少和较多的情况下，误差变化情况不大，但是相较于除Lagrange的其他插值方法，效果一般；线性插值在缺失值少的情况下，取得了较好的插值效果，但随着缺失值的增加，插值效果逐渐变差；Zero阶梯插值随着缺失值的增加，插值效果逐渐变差；Lagrange插值随着缺失值数量增多，均方误差增加较大，表现最差。

从表2和图6至图8可以看出，缺失值较多情况下，所有插值方法中IRFR方法取得了最好的插值效果，且随着缺失值的增加，误差也没有明显增大。

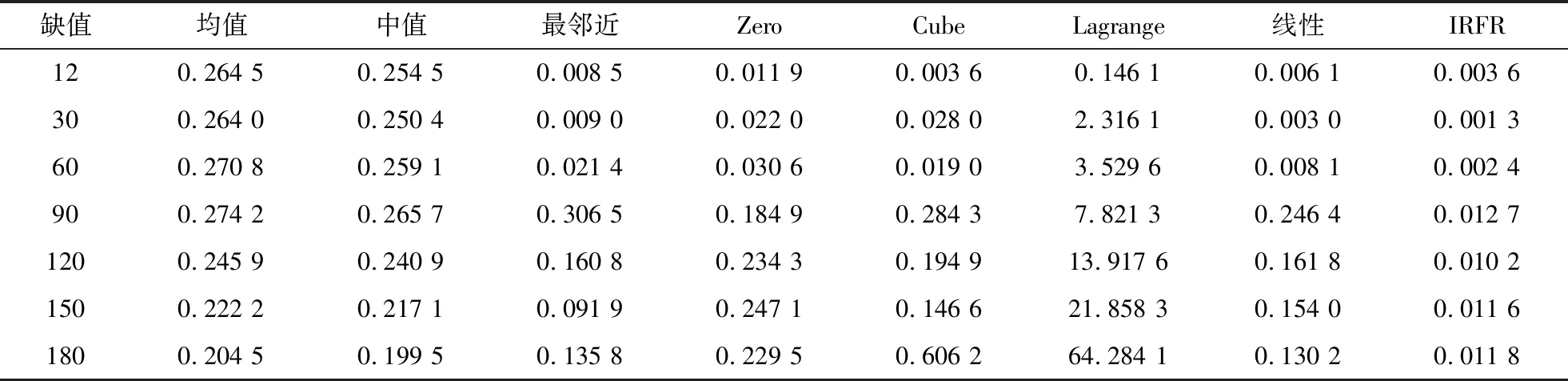
表2 缺失值较多情况下不同插值方法的误差比较Table 2 Errors comparison of different interpolation methods with more missing values

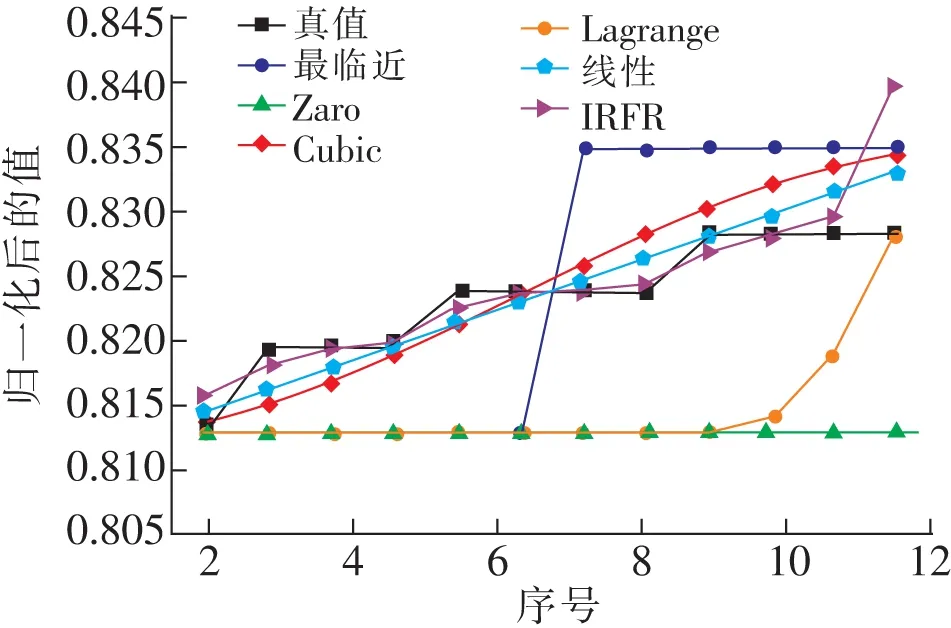
图6 连续缺失12个值情况下的插值效果对比Fig.6 Comparison of interpolation effects in the case of continuous missing 12 values

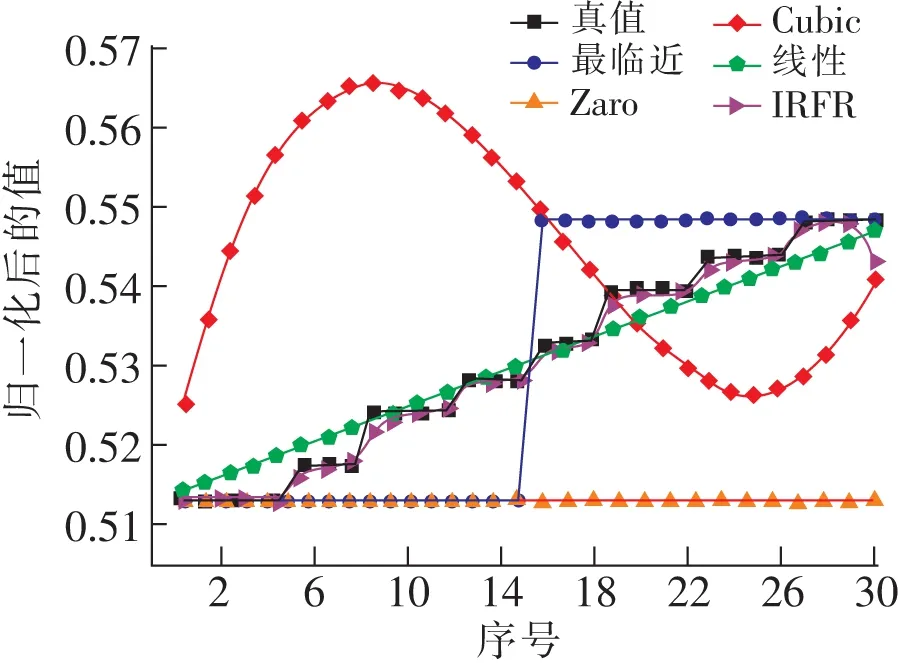
图7 连续缺失30个值情况下的插值效果对比Fig.7 Comparison of interpolation effects in the case of continuous missing 30 values

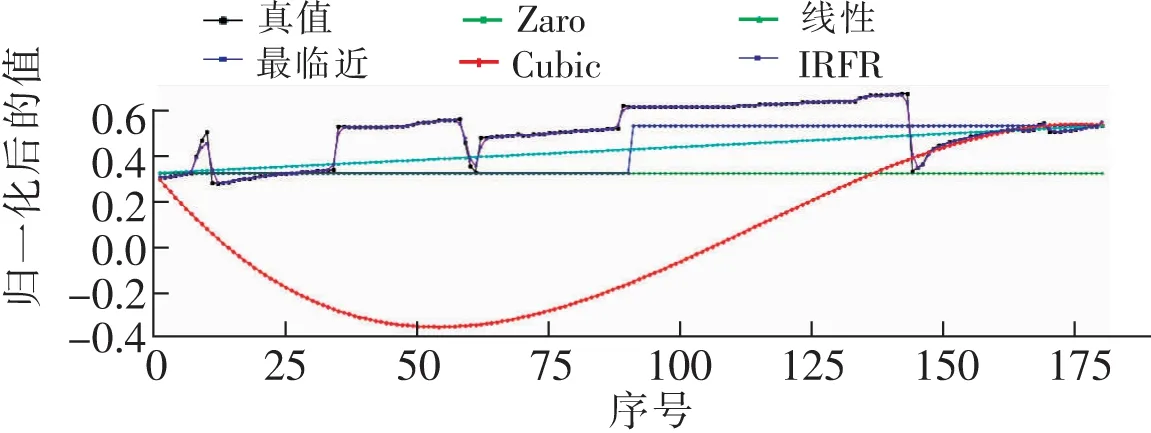
图8 连续缺失180个值情况下的插值效果对比Fig.8 Comparison of interpolation effects in the case of continuous missing 180 values

实验结果表明，针对围岩应力数据，相较于对比的均值插值、中值插值、线性插值、最邻近插值、Zero阶梯插值、3次B样条插值、拉格朗日3次多项式插值插值方法，IRFR方法为最佳插值方法。

4 结 论

1)提出了一种基于随机森林回归预测方法的围岩应力插值方法，该方法利用历史数据训练随机森林回归模型，通过对缺失值进行预测，实现了针对围岩应力时间序列缺失值的插补。

2)对不同缺失值情况下，不同插值方法在围岩应力数据集上的插值效果进行了比较分析。

3)实验结果表明，均值差值、中值插值方法效果较差；拉格朗日插值方法仅适用于缺失值较少的情况，在缺失值较多的情况下，均方误差有随着缺失值数量增多而增大的趋势，效果最差；线性插值、最邻近插值、Zero阶梯插值、3次B样条插值同样适用于缺失值较少的情况，在缺失值较多的情况下效果较差；IRFR方法在不同缺失值情况下，均取得了较好的插值效果，且随着缺失值数量的增加，这种优势尤为明显。因此，IRFR方法适用于围岩应力插值。