X 射线衍射法测定纳米氧化铝的平均晶粒尺寸

王雷雷，王勤隆，李 晶，黄长荣

（万华化学集团股份有限公司，山东烟台264006）

X 射线衍射技术是晶体结构测定与表征、 物相分析、晶粒尺寸计算、结构分析等方面的一种重要方法，在材料科学、物理学及化学等领域的研发和生产中有着广泛的应用［1-5］。 同时，X 射线衍射法具有制样简单、无损分析、测试快捷等优点。 氧化铝陶瓷材料是α-Al2O3为主晶相的陶瓷材料， 具有较高的力学性能、强度、硬度，同时，具有较好的耐腐蚀性、耐高温性及抗化学腐蚀等优点。 在机械、化工、生物医学等领域有重要的应用［6-7］。 晶粒尺寸对氧化铝材料抗压强度、冲击韧性、硬度、耐磨性等有重要的影响［8］。 因此，晶粒尺寸是表征氧化铝材料物理性能和力学性能的一个重要参数。 X 射线衍射法在纳米材料晶粒尺寸分析上有着广泛的应用。

1 实验原理［9］

粉末多晶衍射仪的衍射谱线由一组具有一定宽度的衍射峰组成。 试样在某衍射角度下的实测线性函数h（x），与仪器因素引起的衍射峰线性函数g（x）和样品因素引起的衍射峰线性函数f（x），三者之间存在以下“卷积”关系：

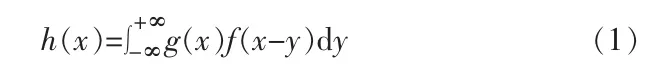
B表示实测衍射峰的宽度，β表示由样品因素引起的宽化，b表示由仪器因素引起的宽化。h（x）为B的函数，g（x）为b的函数，f（x）为β的函数，要从式（1）中解出β是非常困难的。 使用钟罩形函数对式（1）进行简化处理，可得下式：

式（2）中，n为反卷积参数，如果峰形更接近高斯函数，则n=2；如果峰形更接近柯西函数，则n=1。

通过标准样品的测试， 可得出仪器因素引起的宽化值b，据式（2），可分离出样品因素引起的宽化β，样品因素引起的宽化β由两部分构成，晶粒细化引起的宽化β1和微观应变引起的宽化β2，三者之间存在如下关系：

对于不存在微观应变的样品（即β=β1），计算晶粒尺寸D的公式为谢乐公式：

式（4）中，K为常数，常取1；λ为X 射线的波长，nm；β为试样宽化，rad；D为晶粒尺寸，nm。

对于大晶粒的样品， 不考虑晶粒尺寸引起的宽化（即β=β2），计算样品微观应变ε的公式为：

式（5）中，ε为应变量和面间距的比值，用百分数表示。

若样品同时存在晶粒细化和微观应变引起的宽化，将式（4）和（5）带入式（3），则有：

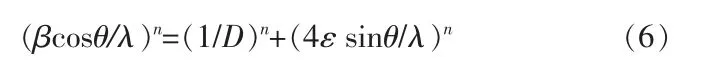
若假定晶粒细化和微观应变引起的宽化函数都遵循高斯函数，则式（6）中n=2，可得：

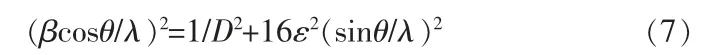
以（βcosθ/λ）2为纵坐标，以（sinθ/λ）2为横坐标作图，求出该直线的截距和斜率，进而求出晶粒尺寸D和微观应变ε，该方法称为高斯分布法。

若假定晶粒尺寸和微观应变引起的宽化函数都遵循柯西关系，则式（6）中n=1，可得：

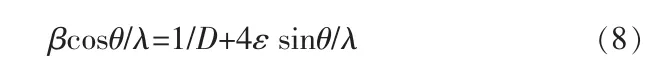
以βcosθ/λ为纵坐标，以sinθ/λ为横坐标作图，求出截距和斜率，进而求出晶粒尺寸D和微观应变ε，该方法最早由Hall 提出，称为Hall 法。

首先介绍Boltzmann方程研究中经常出现的的Povzner不等式，这个不等式将两个分子碰撞前和碰撞后的速度联系起来，在不同的文献中通常有不同的形式，可参考文献[1-3]、[13-14] ， 这里只给出一种形式.

2 实验部分

2.1 仪器及参数

PANalytical X′Pert3 Powder X 射线衍射仪，仪器工作条件：电压为40 kV、电流为40 mA，入射光方向发散狭缝选为系统自动更换， 防散射狭缝为2°，探测器方向的防散射狭缝为9.1 mm。 铜靶Kα波长λ为0.154 nm、2θ在5～80°对样品进行连续扫描，步长为0.013 13°、停留时间为30.6 s、扫描速度为0.109 4（°）/s。

2.2 试剂

NIST-LaB6粉末为标准样品； 高温焙烧得到的Al2O3为待测样品。

2.3 样品制备

采用背压法制样。 将样品环在样品预处理台上夹紧，将粉末样品填入样品环中，使用样品压柱将粉末压实，使用刀片将多余的样品刮掉，将样品杯底板扣在样品环上，取下整个样品杯，保证样品与预处理台接触面平整光滑，并将该面作为测试面。

3 实验结果与讨论

在样品测试前，需要通过标准样品的测试，获得仪器在该实验条件下任意衍射角度下的宽化值。 所谓标准样品，是指结构稳定、无晶粒细化、无宏观应力或微观应力、无畸变的完全退火材料［6］，即认为标准样品不存在晶粒细化和微观应变引起的衍射宽化，测试所得的宽化值（B）即为仪器因素引起的宽化（b）。 本实验以NIST-LaB6为标准样品，计算仪器宽化值。图1 为LaB6标准样品的XRD 谱图，表1 为LaB6标准样品不同晶面的积分宽度值。

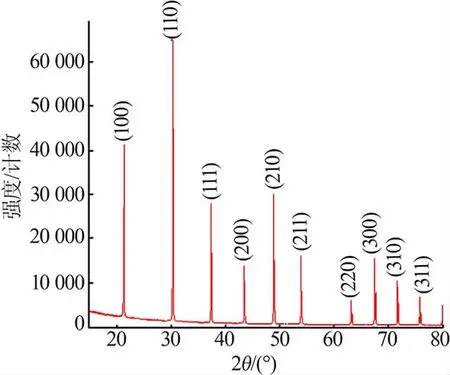
图1 LaB6 标准样品的XRD 谱图Fig.1 XRD patterns of standard LaB6 sample

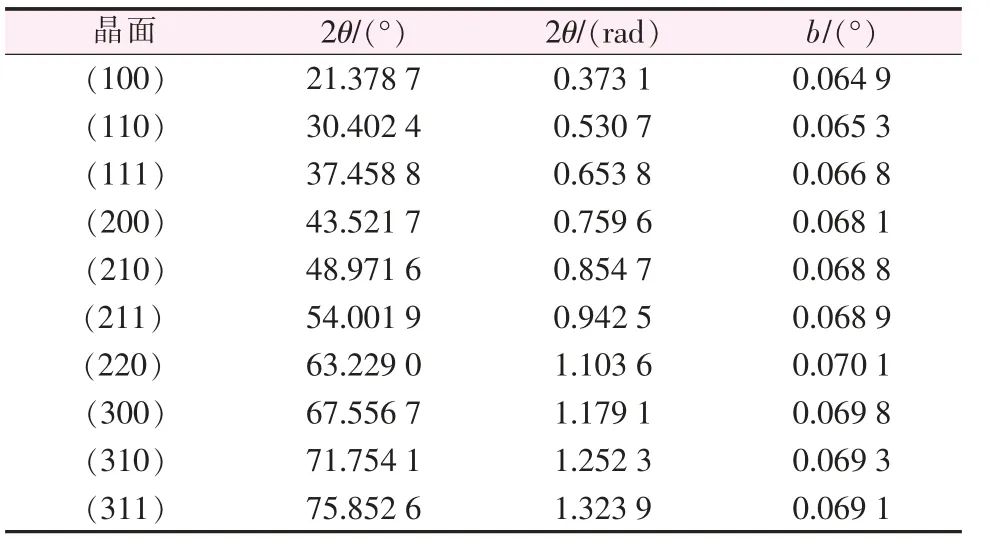
表1 LaB6 标准样品不同角度下的积分宽度值Table 1 Integral widths at different peak position of standard LaB6 sample

由于标准样品和待测样品在不同衍射角度出峰， 需要对标准样品积分宽度随衍射角的变化进行拟合，以便于计算任意衍射角度下的仪器宽化值。通常使用二项式函数对衍射角度和宽化值进行拟合。结果如图2 所示。

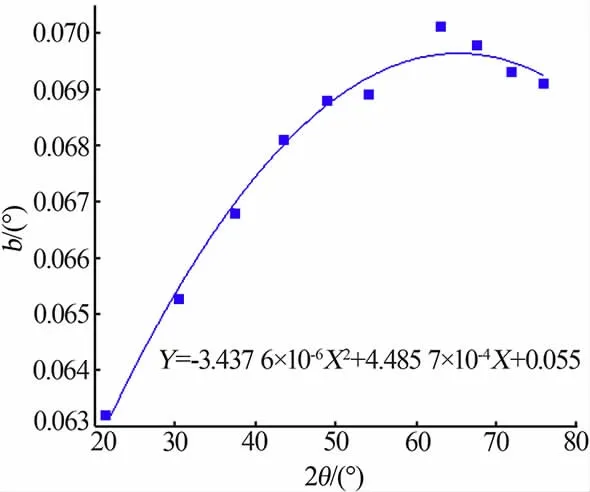
图2 LaB6 标准样品不同角度下的积分宽度值拟合结果Fig.2 Fitting results of integral widths at different peak position of standard LaB6 sample

由图2 可知，不同衍射角度下，标准样品的宽化值（即仪器的宽化值）符合二次函数分布，不同衍射角度下仪器的宽化值符合下式：

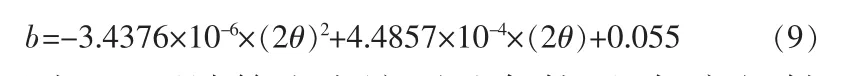
使用式（9）可计算出在该测试条件下，任意衍射角度下的仪器宽化值。

取待测样品Al2O3进行XRD 测试，图3 为该Al2O3样品的XRD 谱图，根据标准卡片匹配，可知该样品与卡片号为01-088-0826 的α-Al2O3标准卡片匹配度很高，因此可判断该Al2O3样品为α型氧化铝，取样品的（012）、（104）、（110）、（113）、（024）、（116）、（214）、（300）8 个强峰晶面进行分析，以此来计算该样品的平均晶粒尺寸。 表2 为该样品8 个强峰晶面的实测衍射积分宽度值B。

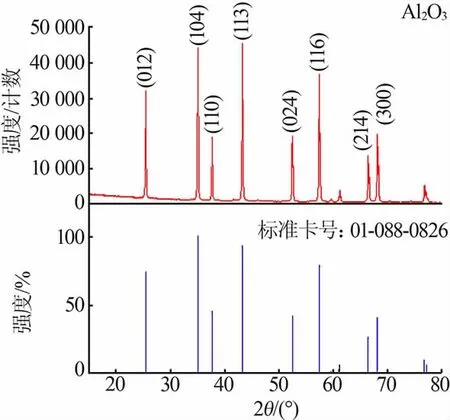
图3 Al2O3 样品的XRD 谱图Fig.3 XRD patterns of Al2O3 sample

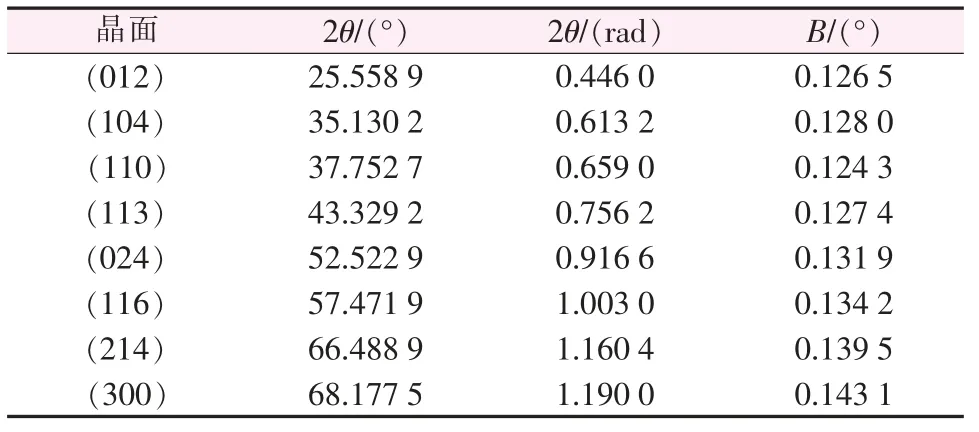
表2 Al2O3 样品不同角度下的积分宽度值Table 2 Integral widths at different peak position of Al2O3 sample

采用高斯分布法，使用式（9）计算出Al2O3样品8 个强峰角度位置下的仪器宽化值b，据式（3）分离出由样品因素引起的宽化值β，据式（7）对Al2O3样品8 个强峰的峰位置和样品因素引起的宽化值β进行拟合。拟合结果如图4 所示。图4 中拟合直线斜率 为0.001 63、 截 距 为1.308 0， 由 此 计 算 该Al2O3样品的平均晶粒尺寸为87 nm、微观应变为0.010 09%。

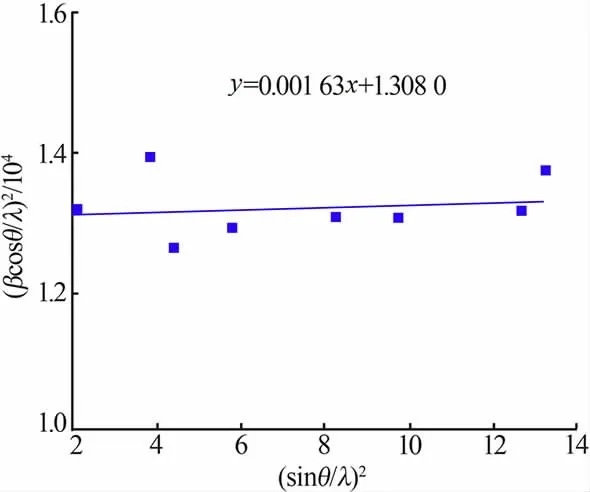
图4 Al2O3 样品的高斯分布法拟合结果Fig.4 Fitting results of Gaussian distribution method of Al2O3 sample

采用Hall 法，使用式（9）计算出Al2O3样品8个强峰角度位置下的仪器宽化值b，据式（3）分离出由样品因素引起的宽化值β，据式（8）对Al2O3样品8 个强峰的峰位置和样品因素引起的宽化值β进行拟合。拟合结果如图5 所示。图5 中拟合直线斜率为0.033 7、截距为6.444 9，由此计算该Al2O3样品的平均晶粒尺寸为155 nm、微观应变为0.000 8%。

高斯分布法与Hall 分布法结果对比，两种方法计算得出的平均晶粒尺寸大小差异较大， 通过衍射图很难判断出衍射峰晶粒细化和微观应变引起的宽化函数更接近于哪种函数关系， 无法据此判断以上两种方法的准确性。 通过两种方法计算得到的微观应变ε 值均小于0.02%， 说明该测试样品本身微观应变很小， 因此衍射峰宽化值绝大部分是由于晶粒细化引起的，可以忽略该样品微观应变引起的宽化，直接采用谢乐公式（式4）对该Al2O3样品的不同晶面的晶粒尺寸进行计算，以此来验证高斯分布法与Hall 法两种计算方法在该样品平均晶粒尺寸测试上的准确性，谢乐公式计算结果如表3 所示。由表3 看出，各晶面晶粒尺寸分布在130～150 nm，与Hall 法测试结果更为接近，因此可判断，该Al2O3样品的衍射峰晶粒尺寸和微观应变引起的宽化函数遵循柯西关系，该样品的平均晶粒尺寸为155 nm。

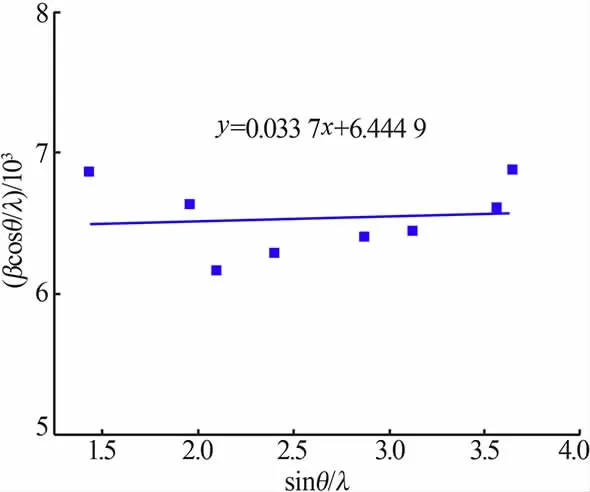
图5 Al2O3 样品的Hall 法拟合结果Fig.5 Fitting results of Hall method of Al2O3 sample

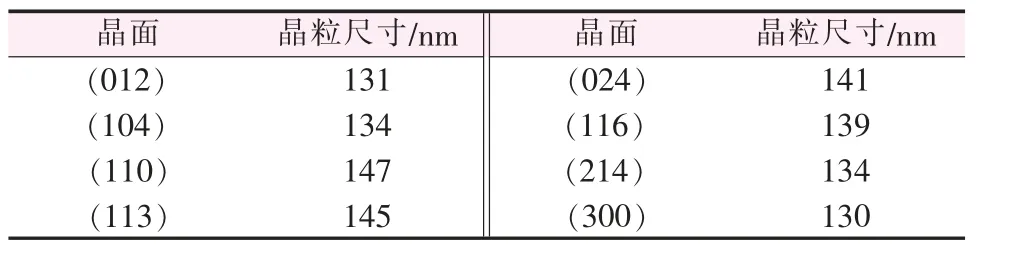
表3 Al2O3 样品不同晶面的晶粒尺寸（谢乐公式）Table 3 Grain size at different crystal face of Al2O3 sample（Scherrer Formula）

4 结论

1）仪器因素和样品因素均会引起X 射线衍射峰宽化， 通过对LaB6标准样品测试结果的拟合，可从实测的宽化值中分离出仪器因素引起的宽化。2）焙烧后的Al2O3样品为α-Al2O3晶型结构。3）该样品晶粒尺寸和微观应变引起的宽化函数遵循柯西函数关系，由Hall 法计算，可知该样品的平均晶粒尺寸为155 nm。