Ni- Re与Co- Re二元体系的热力学研究及相图

史中文 夏成辉 刘 微 鲁晓刚,

(1.上海大学材料科学与工程学院，上海 200444； 2.上海大学材料基因组工程研究院，上海 200444)

20世纪80年代，镍基高温合金成功应用在航空发动机上，这一突破性进展促进了镍基高温合金的迅速发展。目前镍基高温合金广泛用于制造航空航天和许多其他行业的发动机和汽轮机的叶片[1]。

研究表明：在高温合金中添加Re等难熔金属元素可以有效提高高温合金的疲劳性能和抗蠕变性能[2- 3]，但同时会造成元素偏析，在高温服役条件下易析出TCP相，降低合金性能。而Co等元素的添加可以有效地降低难熔元素的偏析，控制TCP相的形成和长大，提高高温合金的高温蠕变性能[4]。确定Ni- Re和Co- Re等合金体系的相图和热力学性质是提高高温合金性能的前提。但目前对于Ni- Re和Co- Re体系的研究还不够充分，导致这两个体系的相图和热力学性质还存在一些问题。虽然近几年由于高温合金的发展，越来越多的研究者开始重视并重新评估这些体系，一些试验数据得到了更新及补全，但仍不够全面。本文结合现有相图试验数据及第一性原理计算结果，重新评估了Ni- Re和Co- Re体系的热力学数据及相图。

1 文献调研

1.1 Ni- Re体系

1985年，Nash等[5]在Savitskii等[6- 7]研究的基础上，结合相平衡试验数据、晶体结构数据等，评估了Ni- Re二元系的相图，但得到的相图与试验数据不太吻合。1992年，Okamoto[8]重新研究了Ni- Re体系，并对以前的部分相图进行了修改，得到了更合理的优化相图。1999年，Huang和Chang[9]利用与Okamoto不同的纯组元热力学数据重新评估了Ni- Re相图，得到了与Savitskii等的试验数据较为吻合的相图。2012年，Yaqoob和Joubert[10]结合近几年的研究数据[11- 12]，提出了新的Ni- Re相图，扩大了hcp相的范围，并对fcc相范围进行了调整，得到了更为准确的相图。

1.2 Co- Re体系

Co- Re体系最早由Koster和Horn[13]研究，Savitskii与Tylkina[14]确定了整个体系的固相线，Elliott[15]则修正了前人研究中的一些问题。1993年，Predel[16]在前人试验数据的基础上重新评估了Co- Re二元体系，并给出了二元系的相图。2005年，Takeuchi和Inoue[17]用Miedema模型计算得到了Co- Re体系4 000 K下的液相混合焓。2014年，Liu等[18]优化了热力学数据并得到了新的Co- Re相图。2018年，Guo等[19]为了建立镍基高温合金数据库重新评估了Co- Re体系，同时也改进了该二元相图。2019年，Fedorayev等[20]在研究Co- Re- Ta体系等温截面时得到了两组Co- Re体系的相平衡数据，但与之前的相图存在差异。

2 第一性原理SQS计算

第一性原理计算(first- principles calculation)方法又称从头计算法(ab initio calculation)，只需要输入元素及结构信息就可以通过薛定谔方程(Schrödinger equation)合理预测材料的各种物理化学性质和电子状态[21]。密度泛函理论(density functional theory,DFT)[22]是第一性原理计算的基础，其主要目标是用电荷密度函数代替复杂的多电子波函数作为基本变量，从而实现电子结构的计算。

本文利用VASP(Vienna ab initio simulation package)软件包[23]，采用平面波方法和投影缀加波(projected augmented wave,PAW)[24]赝势法，交互关联泛函采用GGA- PW91[25]，进行了自旋极化计算，设置了铁磁性的磁性参数。平面波截断能取400 eV。使用Monkhorst- Pack包[26]构造布里渊区k点网格，k点的总数乘以单胞的原子数至少为7 200。利用特殊准随机结构(special quasirandom structures, SQS)[27]方法产生无序结构，构建了16个原子的超胞，包括如下成分结构，即A1B15、A4B12、A8B8、A12B4和A15B1。为了在VASP计算过程中自动产生输入文件以方便计算，本文使用了ZenGen脚本工具[28]。

3 试验材料与方法

将纯度(质量分数)均为99.99%的Ni、Re和Co 3种纯金属原材料按照合金成分进行称重配料，制备试样。采用WK- II型电弧感应熔炼炉熔炼，得到所需成分的合金纽扣锭。随后将试样密封在氩气保护的石英管中，再将石英管置于马弗炉中加热至1 473 K保温72 h后水淬，以消除偏析并提高成分均匀性。将淬火后的试样线切割加工成4 mm×4 mm×4 mm的正方体和直径4.9 mm、高度18 mm的圆柱样，然后清洗除去表面油污，并用金相砂纸打磨抛光，确保后续处理不会有杂质影响。将正方体试样密封在氩气保护的石英管中，然后置于管式炉中加热至一定温度，保温一定时间后水淬，具体方案如表1所示。正方体试样经打磨抛光后采用电子探针(EPMA)测定相成分。最后使用MHTC96高温量热仪对圆柱形试样进行差热扫描分析(DTA)，测定其相变点。

表1 合金成分及试验条件Table 1 Compositions of the alloy and experimental conditions

4 热力学模型

Ni- Re和Co- Re体系中的液相、fcc和hcp相都可以采用置换溶体模型来描述，其摩尔吉布斯自由能函数为：

(1)

(2)

(3)

5 结果与讨论

5.1 Ni- Re体系

1999年Huang和Chang[9]重新评估了Ni- Re相图，得到了与Savitskii等[6- 7]的试验数据较为吻合的相图。但是近些年对Ni- Re体系的一系列研究都表明hcp相的实际相区更大，并且在富Ni端的试验数据也与计算相图不符，故Yaqoob和Joubert[10]结合近几年的研究数据[11- 12]，提出了新的Ni- Re相图，具体数据列于表2。如图1所示，Yaqoob和Joubert计算得到的相图中hcp相区较Huang和Chang的明显扩大，且对fcc相区进行了调整，与近些年的Ni- Re的相平衡数据比较吻合。

本文对Yaqoob和Joubert[10]计算得到的相图也进行了验证。将Ni- 30Re合金(1号合金)在1 523 K保温72 h得到了一组相平衡数据，发现平衡点与Yaqoob和Joubert的结果十分接近。此外，对Ni- 30Re合金进行了DSC测试，测得其包晶温度为1 832.98 K，比Yaqoob和Joubert的计算结果略高。

表2 Ni- Re相平衡试验数据Table 2 Experimental data of the Ni- Re phase equilibrium

图1 优化的Ni- Re相图与试验数据对比Fig.1 Comparison of the optimized Ni- Re phase diagram with the experimental results

但研究发现，Yaqoob和Joubert[10]在热力学评估时仅考虑了相平衡点数据，并未考虑其他热力学性质，在外推到高元体系时容易产生问题，所以本文在相平衡数据的基础上，同时考虑其他热力学性质，以得到更为准确的热力学参数。

Hofmann[29]研究发现，当Re的质量分数达到18%左右时，Ni- Re系合金中fcc相的居里转变温度为273 K；当Re的质量分数达到30%左右时，居里温度接近0 K。Huang和Chang[9]及Yaqoob和Joubert[10]的评估都未涉及此问题。本文对此进行了研究，基本能反映Ni- Re合金的居里温度随合金成分变化的规律，对比结果如图2所示。此外，还对第一性原理SQS计算所得的混合焓及磁矩进行了研究，结果如图3和图4所示。

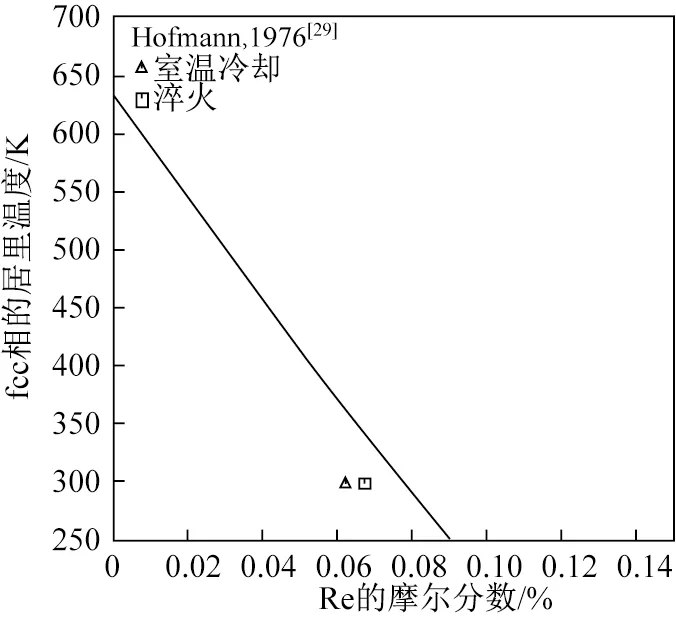
图2 Ni- Re体系fcc相优化的居里温度与试验数据对比Fig.2 Comparison of the optimized Curie temperature of fcc phase in Ni- Re system with the experimental data

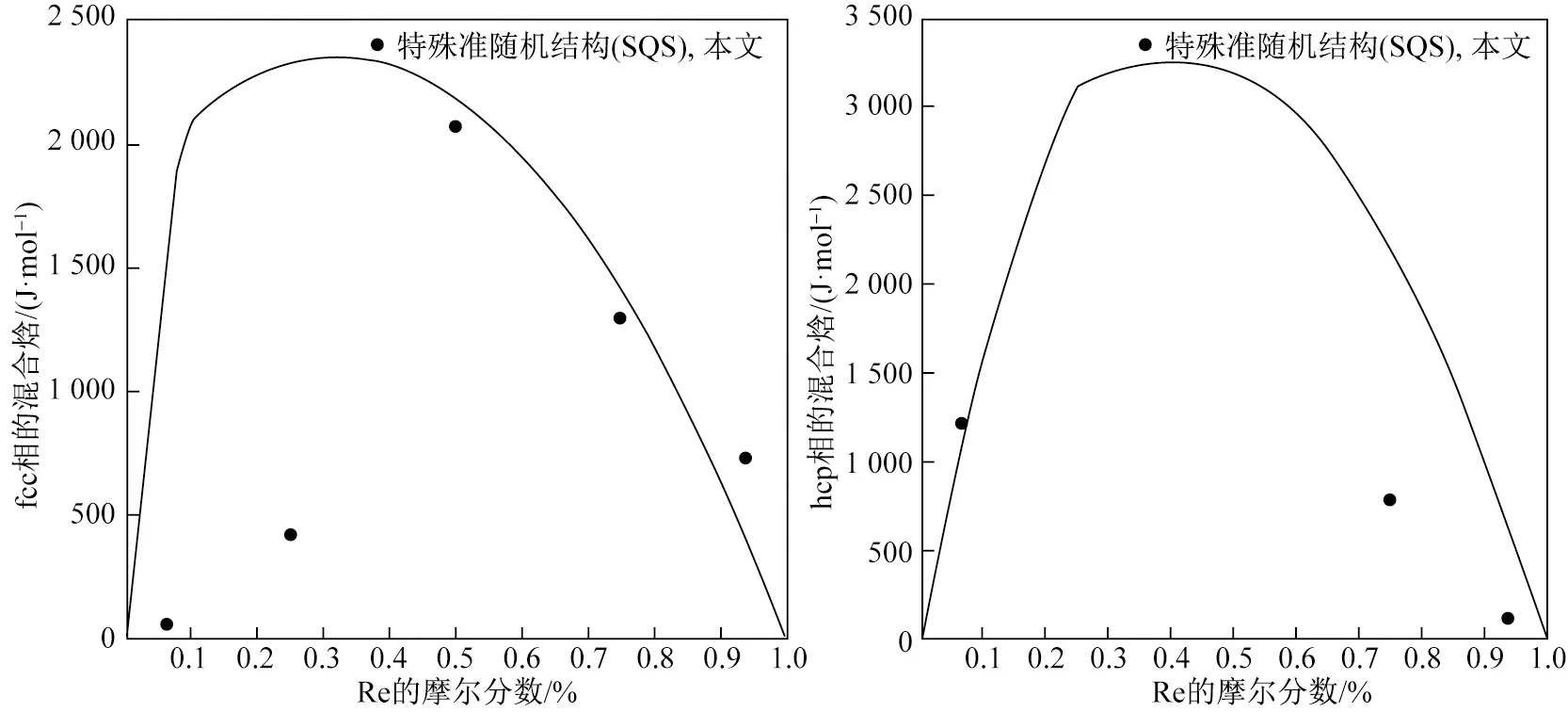
图3 优化的Ni- Re fcc相和hcp相的混合焓与特殊准随机结构(SQS)数据的对比Fig.3 Comparison of the optimized mixing enthalpy of fcc and hcp phases in Ni- Re system with the SQS data

图4 优化的Ni- Re fcc相和hcp相的磁矩与特殊准随机结构(SQS)数据的对比Fig.4 Comparison of the optimized magnetic moment of fcc and hcp phases in Ni- Re system with the SQS data

综合以上研究重新评估得到新的相图如图1所示。与Yaqoob和Joubert[10]的相图相比， 新相图中的包晶反应温度提高，该温度下Ni在Re中的最大溶解度增大，与本文试验数据更为吻合，同时也与其他数据较为符合。

5.2 Co- Re体系

Liu等[18]在前人研究的基础上优化了Co- Re相图。2018年，Guo等[19]为了建立镍基高温合金数据库，重新评估了Co- Re二元系的试验数据，优化了该体系的相图。Liu等与Guo等评估的相图与试验数据的比较如图5所示。从图5可以看出，两者差别不大，仅在溶解度曲线上略有差异，并且从文献中可知，二者均未找到原始试验数据，都是从Predel[16]的试验相图上描点来验证各自计算相图的。由于缺乏试验数据，对现有Co- Re体系相图的准确性还无法有效验证。

2019年，Fedorayev等[20]在研究Co- Re- Ta体系等温截面时得到了两组Co- Re体系的相平衡数据，如表3所示。可见，Fedorayev得到的平衡点与现有相图差异较大，相对于原来的相界向右偏移，落在了现有相图的两相区和hcp相区。为了验证现有相图的准确性，本文也进行了试验研究，结果如图5所示，发现预计落在两相区的合金点是单相，表明现有相图存在问题，需进一步研究。

图5 优化的Co- Re相图与试验数据对比Fig.5 Comparison of the optimized Co- Re phase diagram with the experimental data

Guo等[19]在研究Co- Re体系时，引入了一系列热力学参数，但未与试验数据进行比较，所以无法判断这些参数的准确性。本文根据第一性原理SQS计算得到的混合焓及磁矩，对Co- Re体系的热力学参数进行了重新评估，对比结果如图6和图7所示。可见用当前热力学参数计算的结果与第一性原理计算结果较吻合。此外，Takeuchi和Inoue[17]利用Miedema模型计算得到了Co- Re体系4 000 K下的液相混合焓，与本文试验数据的对比如图8所示，两者吻合较好。

表3 Co- Re相平衡试验数据Table 3 Experimental data of the Co- Re phase equilibrium

图6 优化的Co- Re fcc相和hcp相的混合焓与特殊准随机结构(SQS)数据的对比Fig.6 Comparison of the optimized mixing enthalpy of fcc and hcp phases in Co- Re system with the SQS data

图7 优化的Co- Re fcc相和hcp相的磁矩与特殊准随机结构(SQS)数据的对比Fig.7 Comparison of the optimized magnetic moment of fcc and hcp phases in Co- Re system with the SQS data

图8 优化的4 000 K下Co- Re液相的混合焓与试验数据的对比Fig.8 Comparison of the optimized mixing enthalpy of liquid phase in Co- Re system at 4 000 K with the experimental data

综合以上结果，重新计算得到的新相图如图5所示，与Liu等[18]及Guo等[19]的相图及试验数据进行对比，发现新相图的两相区右移，与Fedorayev等[20]的试验数据基本一致，并且单相区范围与试验结果一致，表明本文优化的相图更为合理。

6 结论

运用CALPHAD方法和Thermo- Calc软件，结合近年文献及本文测定的试验数据，加之第一性原理SQS计算结果，重新评估了Ni- Re和Co- Re二元体系，得到了新的二元相图以及一系列热力学参数。计算得到的相图和热力学性质与试验数据、第一性原理计算结果自洽良好。新相图及热力学数据可以作为外推高元体系的基础，对镍基高温合金的研究具有重要意义。