基于高精度位移测量的水平差应力系数计算方法
2021-04-08秦雨樵吴振君
秦雨樵,汤 华,吴振君
(1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点试验室,湖北 武汉 430071; 2.中国科学院大学,北京 100000)
页岩气作为一种重要的非常规天然气,在自然界储量丰富,具有极大的开采价值。根据测算,世界页岩气的资源量超过4×1014m3,接近非常规天然气总量的1/2[1]。从我国土资源部油气资源战略中心发布的《全国页岩气资源潜力评价及有利区优选报告》中,全国的页岩气地质资源潜力超过130万m3,其中可采资源潜力超过20万m3。而在评价页岩气储层可采性的诸多指标中,地应力参数是十分重要的。水平地应力差异系数是最大最小水平主应力之差与最大水平主应力之比[2]。水平差应力系数越小,水压裂隙越倾向形成相互交织的网状体系,有利于页岩气的析出。
地应力测试以及估算方法发展近60年,基于不同的计算原理延伸出很多的不同方法,其中包括水压法[3-7]、解除法[8-10]、千斤顶法[11]、应变恢复法[12-14]等。其中,应力解除法是通过分离测试点与其周围岩体,使其应力完全得到释放,并测量记录这一过程中的变形情况。最后利用变形与远场地应力张量之间的关系,结合岩体变形参数,引入最小二乘法计算原理,就能确定地应力状态。目前,常用的几种应力解除法设备,比如套芯解除装置[8]、CSIR(Council for Scientific and Industrial Research)三轴应变测试单元[15]、空心包体测试设备[10,16],均是首先在工作面钻一大孔,远离应力扰动区域后在孔底钻一先导孔;然后将设备置于先导孔中,再下入大钻头进行应力解除操作;最后取出岩芯,在室内开展双轴压力试验,确定岩体变形参数。由于大部分设备只能在孔底进行应力解除,使得应力解除法受到钻孔孔深的限制,只适用于地下硐室或者采矿巷道中,直接运用在垂直钻孔中的实例集中在400~500 m的深度范围内。
葛修润院士[17]于2004年提出了一种新的地应力测试方法——局部壁面应力解除法,该方法克服了传统应力解除法选择在孔底进行解除作业的限制,可在任意深度的测试孔段侧壁进行多次应力解除作业,并测量记录测量点的变形情况,从而反算得到地应力场。目前依据该方法研制的局部壁面应力解除法地应力测试机器人(BWSRM-H01)已在锦屏水电站进行了实地测试,取得了良好效果[18-19]。然而,在将该设备往深垂直钻孔中开展下一步工作中,发现其测试条件与浅表处存在很大的不同,主要是受到温度变化、钻井液压力等很多条件限制[20]。这使得在井下粘贴应变花的难度大大增加。
为了解决上述问题,本文在局部壁面应力解除法的基础上,提出一种基于高精度位移测量的水平差应力系数计算方法。首先,根据弹性力学基本原理,推导出孔壁径向位移与远场地应力的关系,通过获取3个不同方向上的径向位移,即能计算得到最大、最小水平主应力,从而得到水平差应力系数;然后,建立有限元模型,对上述公式进行验证;最后,讨论了孔壁压力、温度变化等条件下对地应力测试的影响。
1 理论介绍
理论模型以及坐标系如图1所示。

图1 理论模型以及坐标系示意Fig.1 Theoretical model and coordinate system sketch
由于孔径相对于钻孔长度而言很小,将问题简化为平面应变问题考虑(图1)。假设在一均值、连续、各向同性线弹性薄板中存在一钻孔,半径为R,钻孔周围某一点到钻孔轴线的距离为r。定义局部坐标系oxy,在边界处,受到单向压力p作用。建立局部柱坐标系orθ,其中角坐标θ从ox轴正向开始。在局部坐标系中,各地应力表示为Sxy、Syy和Sxy;在局部柱坐标体系下,应力分量表示为σr、σθ、γrθ,应变分量表示为εr、εθ、γrθ,位移分量表示为ur、uθ、urθ。在局部坐标系下,应力函数φ与σr、σθ、γrθ之间的关系可以表述为:
(1)
(2)
(3)
边界条件可以表示为:
(4)
(5)
(σr)r=b=(τrθ)r=b=0b=R
(6)
应力函数的形式可以表示为:
φ=alnr+Br2+(Cr2+Dr-2+F)cos 2θ
(7)
一般情况下,钻孔受到水平向地应力σx、σy和τxy的作用,则在此条件下,孔壁附近各应力分量为:
(8)
(9)
(10)
根据平面应变模型中应力—应变关系以及应变与径向位移之间的关系,则钻孔附近径向位移与位移的关系可以表示为:
(11)
在井壁处r=R,则井壁处径向位移为:
(12)
从式(12)中可以看出,孔壁处径向位移可由远场地应力、弹性参数计算得到,所以只要能获取到足够多不同方向上的位移,就能解算出远场地应力分量。要达到这一目的,就需要对某一测试井段范围内解除3处测试点的应力,并通过高精度位移传感器测量解除过程中的径向位移变化。为了防止测试点互相干扰,间隔120°,角度为θ=270°、30°以及150°,则3处的径向位移分别为:
(13)
(14)
(15)
通过求解式(13)—式(15),这样远场地应力分量可以表示为:
(16)
(17)
(18)
再由远场地应力分量与水平主应力之间的关系可以得到:
(19)
(20)
最大最小水平主应力的方向为:
(21)
(22)
最终得到该段的水平差应力系数:
(23)
2 数值验证
为了验证推导出的水平差应力系数计算公式,用Phase2D建立有限元计算模型(图2)。模型为边长1 m的正方体,中心处有一半径为130 mm的钻孔,共包含单元5 536个,节点11 193个。

图2 数值计算模型Fig.2 Numerical calculation model
边界应力场参考Yang等关于中国大陆浅层地壳构造应力场的研究成果,地应力与深度(0~4 km)的关系可以表示为:
σH=0.22 9D+4.738
(24)
σh=0.017 1D+1.829
(25)
取测试深度为3 km,则主应力σH=75.438 MPa,σh=53.129 MPa。
计算中,弹性模量为24.910 GPa,泊松比为0.324。为了分析应力解除过程对位移测量的影响,环形切割的内径为30 mm,解除深度为60 mm,分为
10步解除完成,每步6 mm。考虑2种地应力场工况:工况一,最大水平主应力方向与x轴一致;工况二,最大水平主应力方向与y轴一致。
图3展示了不同解除深度(从步骤2开始,每步解除6 mm)下,测试点1处的径向应力σr与切向应力σθ的变化情况。对于切向应力σθ,随着解除深度的增加,其大小迅速降低,当解除深度达到18 mm时,应力已经趋近为0。而径向应力σr则呈现先增后减的变化规律,并且下降幅度较切向应力慢,直到解除深度为48 mm时,应力才为0,此时解除的深度为解除直径的1.6倍。与传统解除法要求2.5~3.0倍直径的解除长度相比大大减小,这样遇到软弱结构面的概率降低,岩芯不易中途折断、损坏,测试的成功率也提高了。
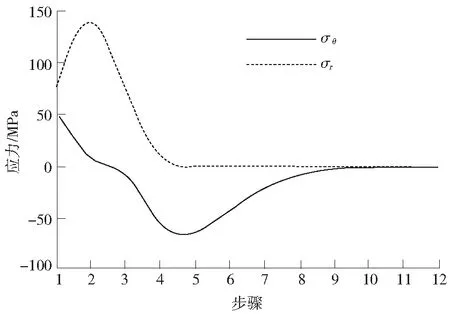
图3 测试点1处应力随解除深度变化Fig.3 Stress at test point 1 changes with release depth
图4展示了解除测试点1与测试点2时对于孔壁应力的影响范围。在解除了测试点1后,在198°的范围内,应力均受到这一解除过程的影响,但对测试点2以及测试点3的应力状态没有影响。解除测试点2后,这一范围达到285°,测试点3的应力状态同样也没有影响。这说明间隔120°的布置情况能够满足测试地应力的要求,在解除任意一点处的应力过程中,不会对其他未测试的测试点的应力状态造成扰动。

图4 解除测试点后对孔壁应力的扰动范围Fig.4 Disturbance range of hole wall stress after releasing test point
首先统计工况一的3个测试点的径向位移以及角度(表1,图5)。因为在计算工程中,未考虑天然地应力场的作用,而只考虑了应力重分布的作用,所以通过双向压力状态公式对数值计算的结果进行修正,得到数据代入式(16)—式(18)中,得到σx=75.145 MPa,σy=52.880 MPa,DHSR=0.296。可以看出,与初始设置的边界条件一致。
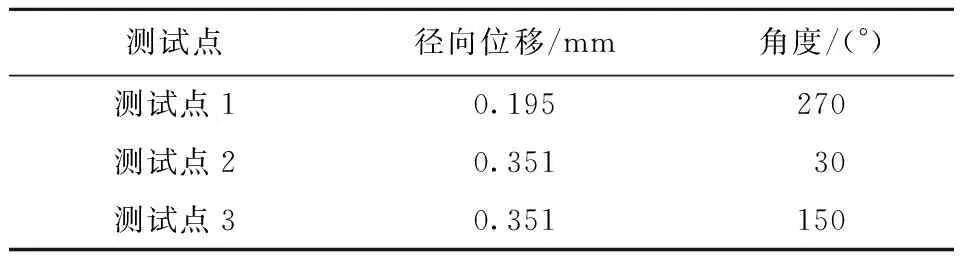
表1 工况一测试点位移统计Tab.1 Displacement statistics of test point in condition 1

图5 工况一位移分布Fig.5 Displacement distribution of working condition 1
同样,在工况二中(表2,图6),反算得到的地应力场分量为σx=53.094 MPa,σy=74.503 MPa,DHSR=0.287。

图6 工况二位移分布Fig.6 Displacement distribution in condition 2

表2 工况二测试点位移统计Tab.2 Displacement statistics of test point in condition 2
这2个实例说明,只要能较精确地获得孔壁处的位移,利用式(23)能求解得到水平差应力系数。
3 讨论
3.1 钻井液作用
井筒失稳是石油工业中最严重的问题之一。它会导致钻井过程的延迟、钻井成本的增加,在某些情况下甚至会导致油井的废弃。要抑制钻井崩塌的发展,钻井液的调配非常关键。在钻井前,岩体处于应力平衡状态;而在钻井后,液柱压力提供了井壁支撑力,需要重新与地应力、孔隙压力等其他应力形成平衡。如果压力偏低,井壁岩石容易产生剪切破坏。如果是塑性岩石则会导致缩径,如果是脆性岩石则会发生孔壁崩塌,造成井径扩大。为了说明这一点,在本文建立的模型上,采用弹塑性模型计算塑性区的范围。
岩体破坏本构方程采用摩尔—库仑破坏准则,内摩擦角为33.86°,黏聚力为8.98 MPa。目前常用于页岩气钻孔的钻井液密度为1.9 ~2.3 g/cm3,若深度为3 km,则液柱压力的大小在60 MPa附近,本次分析中考虑液柱压力分别为0、20、40、60 MPa这4种情况下,孔壁周围的屈服单元分布情况(图7)。可以看出,在无液柱压力条件下,孔壁一定范围内出现大量屈服单元,并相互贯通,表明在此条件下已经发生整体失稳破坏。当液柱压力为20 MPa时,屈服区主要集中在孔壁左右两端,与最大主应力的方向一致,说明发生局部失稳。当液柱压力大于40 MPa时,孔壁周围无屈服单元产生,此为满足井壁力学稳定的下限值。同时也说明,在深部钻孔环境量测地应力时,必须要在有压条件下进行,所以需要修正公式。

图7 不同水压情况下孔壁屈服区分布Fig.7 Distribution of yield zone of hole wall under different water pressure
若考虑液柱压力pw的影响,公式变为:
(26)
(27)
(28)
将式(26)—式(28)同样代入公式中,得到考虑液柱压力条件下的孔壁周围位移分布规律:
(29)
令r=R,则在孔壁处径向位移为:
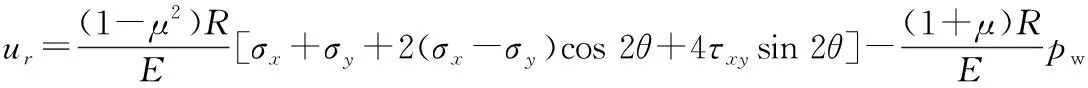
(30)
则式(26)—式(28)变为:
(31)
(32)
(33)
表3统计了有液柱压力条件下工况一各测试点的位移值,不难发现所得到的径向位移均小于无液柱压力条件下的位移,甚至在测试点1处的位移发生反向,这均是液柱压力的作用。如果仍然将该结果代入公式进行计算,得到σx=31.043 MPa,σy=8.749 MPa,与预设地应力完全不符。代入改进公式中进行计算,得到σx=75.422 MPa,σy=53.128 MPa,基本与预设地应力相符,说明改进公式的正确性。

表3 有液柱条件下工况一测试点位移统计Tab.3 Displacement statistics of test point under condition 1 with liquid column
3.2 误差分析
要在深部钻孔进行局部壁面应力解除作业,需要克服诸多复杂条件的限制,这些条件均会影响测试的精度以及具体实施的可行性。
(1)位移传感器的测量精度。为了简单估算变形的大致范围,以地层深度为3 km为例,平均地应力约为50 MPa,弹性模量约为20 GPa,则应变的大小预估为2.5×10-3。再因侧壁解除所使用的钻头直径一般为30 mm,则位移量约为75×10-3mm。而目前,采用光栅刻度尺的高精度接触式位移传感器已经达到1×10-3mm的测试精度,并具有一定的防水防潮功能,下一步则是在此基础上增加其耐压功能,能够在深部高水头的条件下正常工作。
(2)由岩体非均质性以及软弱结构面导致的不确定。由于该方法是基于线弹性、连续体的假设推导得到的,如果在解除过程中岩芯出现节理、软弱层面等不连续面,会对测试结果产生影响,甚至会导致测试过程完全失败,这是所有应力解除方法都存在的通病。但本方法较传统方法具有解除深度浅、解除时间短的优点,能显著提高试验的成功概率。要提高测试精度,可以结合钻孔摄像、测井资料,选择完整性好、节理面少甚至没有的孔段,进行侧壁应力解除。
(3)要求解水平地层差应力系数,还需要获取岩体变形参数(弹性模量、泊松比)以及钻孔的半径,所以这些参数对测试精度也十分重要。此方法在应力解除测试过程结束后,可以通过钻头的上下纵移将岩芯取出,回收至岩芯仓中,待返回地面后再进行室内试验,求取岩体变形参数。而由于各种因素可能导致钻孔缩径或者扩孔,对计算产生影响,故通过井下电视或者测井工具测量孔壁形态,对钻孔直径进行修正,能显著提高整体的测试精度。
4 结论
本文提出了一种基于高精度位移测量的水平差应力系数计算方法,结合有限元计算模型,进行了验证。同时考虑钻井液的存在,修正了所提出的公式。
(1)基于弹性力学原理,得到孔壁径向变形与远场水平地应力、岩体变形参数(包括弹性模量、泊松比)以及钻孔半径之间的关系式。要求解这一方程,需要获取3个不同方向上的径向位移。
(2)当岩芯直径为30 mm时,环切深度达到48 mm即能满足完全应力解除的要求,与传统应力解除法相比大大缩短,能显著提高测试的成功率。
(3)通过有限元计算模型,对所推导的公式进行验证。结果表明,逆推得到的地应力分量与预设地应力分量基本一致,表明公式的正确性。同时,数值结果表明,在同一平面上间隔120°布置3个测试点,解除其中任一测试点的应力不会对其他测试点的应力产生干扰。
(4)钻井液的液柱压力是维持井壁稳定性的最重要因素之一,结果表明,在3 km深度条件下,液柱压力达到40 MPa以上,才能确保井壁附近无屈服区参数。也说明在计算过程中,必须要考虑钻井液液柱压力的作用,所以对提出的公式进行了修正,并采用数值计算验证了公式的正确性。
(5)该方法误差主要来自位移测量误差、岩体软弱结构面产生的误差以及岩体变形参数、钻孔形态不均匀的测量误差,并给出了相对应的控制措施,以确保最终结果的准确性。
总之,本文提出的水平差应力系数计算方法能不受孔深的限制,测试时间短,成功率高,将为页岩气资源勘探评价以及开发提供基础数据,具有十分重要的意义。
