SOME SPECIAL SELF-SIMILAR SOLUTIONS FOR A MODEL OF INVISCID LIQUID-GAS TWO-PHASE FLOW∗
2021-04-08JianweiDONG董建伟
Jianwei DONG(董建伟)
School of Mathematics,Zhengzhou University of Aeronautics,Zhengzhou 450015,China E-mail:dongjianweiccm@163.com
Manwai YUEN(阮文威)†
Department of Mathematics and Information Technoligy,The Education Unicersity of Hong Kong,10 Lo Ping Road,Tai Po,New Territories,Hong Kong,China E-mail:nevetsyuen@hotmail.com
Abstract In this article,we are concerned with analytical solutions for a model of inviscid liquid-gas two-phase flow.On the basis of Yuen’s works[25,27–29]on self-similar solutions for compressible Euler equations,we present some special self-similar solutions for a model of inviscid liquid-gas two-phase flow in radial symmetry with and without rotation,and in elliptic symmetry without rotation.Some blowup phenomena and the global existence of the solutions obtained are classified.
Key words two-phase flow;analytical solutions;self-similar;blowup;global solutions
1 Introduction
Over the course of the last several decades,two-phase and multi-phase flows have attracted the attention and interest of many researchersbecause they have many applications in aerospace,chemical engineering,micro-technology and other fields.Many works on the well-posedness and blowup criterion of various models of two-phase flows have been published;we refer readers to[2,3,5–12,17–23]and the references therein.We are interested in the mixed flow of liquid and gas,which is used to model boilers,condensers,pipelines for oil and natural gas,etc..In this article,we consider the following compressible inviscid liquid-gas two-phase isentropic flow of drift-flux type [12]:
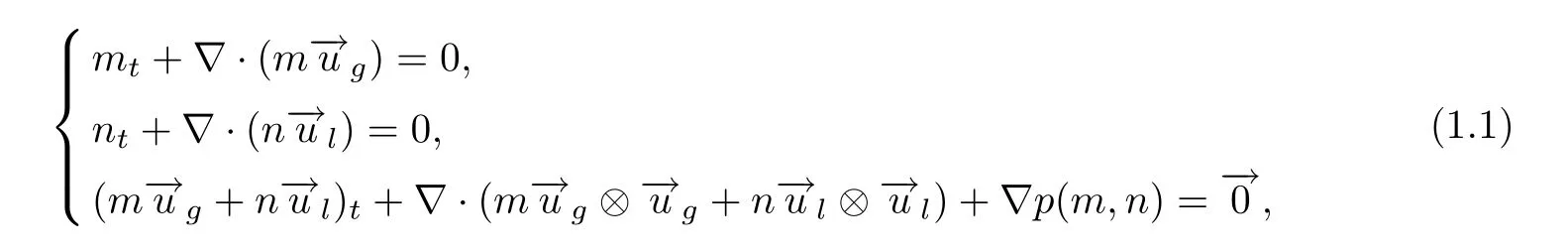


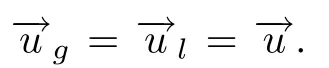

In [12],Huang,Wang and Yuan obtained the nonlinear stability and existence of compressible vortex sheet solutions to (1.3) under small perturbations using a modification of the Nash-Moser iteration technique.In this article,we are interested in the analytical solutions to(1.3).Searching for particular analytical solutions to a system of fluid flow is an important part of mathematical physics for understanding its nonlinear phenomena.

The rest of this article is organized as follows:in Section 2,we present some special selfsimilar solutions to (1.3) in N-dimensional radial symmetry without rotation and give their blowup phenomena or global existence.In Section 3,we consider the case of N-dimensional elliptic symmetry and non-rotational flow.For the rotational flow,we consider the two-dimensional and three-dimensional radial symmetry cases in Sections 4 and 5,respectively.Some conclusions and discussions are included in Section 6.
2 Radial Symmetry and Non-rotational Flow


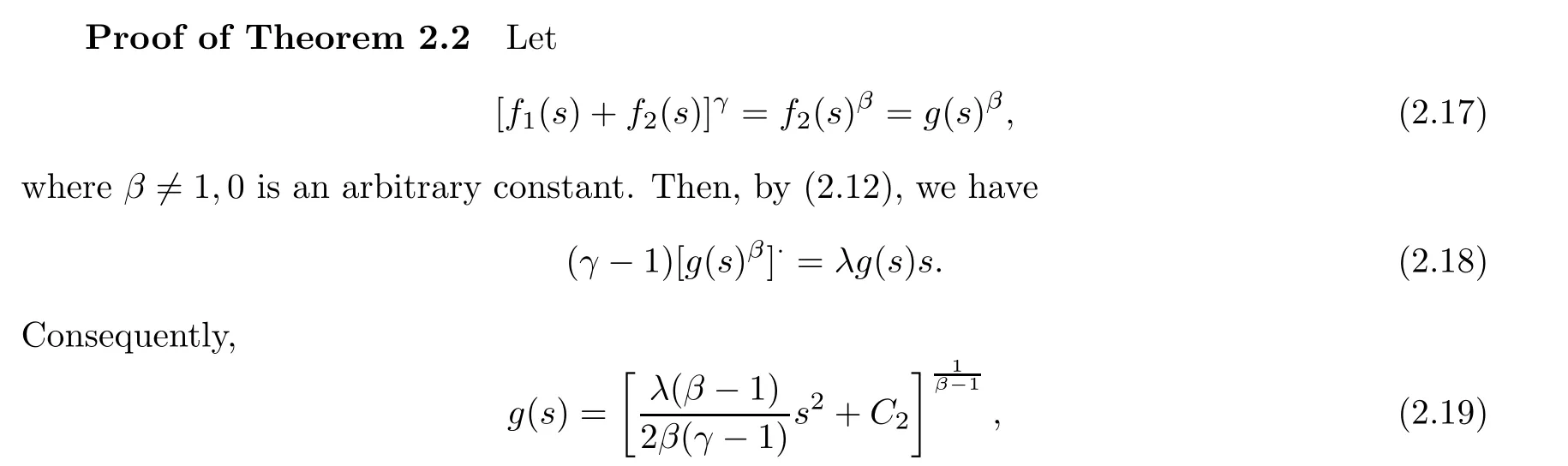

Proof of Theorem 2.3
Let

By using the analysis of the Emden equation (2.4) in Corollary 2.3 of [15],we deduce the following corollary:
Corollary 2.6
For the self-similar solutions obtained in Theorems 2.1–2.3,we have that(1) if λ<0,the solutions are global;
(2) if λ ≥0,

is the escape velocity.If a≥v,the solutions are global;if a In a fashion similar to Section 2,we present three families of self-similar solutions with elliptic symmetry to (1.3) for non-rotational flow. With Lemma 3.5,we can prove Theorems 3.1–3.3 by choosing some special relations between f(s)and f(s).Because the proof is similar to those of Theorems 2.1–2.3,we omit the details. By Theorem 1 of [28],we obtain the following corollary: Corollary 3.6 (1) if ξ <0 and some a<0,then the solutions blow up on or before the finite time (2) if ξ >0 and a≥0,i=1,2,···,N,then the solutions exist globally. We present three families of self-similar solutions with radial symmetry to (1.3) for 2D rotational flow. (1) if 1<γ <2 and E(0)<0,the solutions are time-periodic;otherwise,the solutions are global; (2) if γ=2 and (2aI) ξ>−λ or ξ=−λ with a≥0,the solutions are global; (2aII) ξ=−λ with a<0,the solutions blow up at T=−a/a; (2b) ξ<−λ,the solutions blow up at a finite time if otherwise,the solutions are global; (3) if γ >2 and (3a) if λ ≥0,the solutions are global; (3b) if λ<0 with (3bI) a≥a,if E(0)≤F(a) or E(0)>F(a) with a≥0,the solutions are global;otherwise,the solutions blow up at a finite time; (3bII) a We present three families of self-similar solutions with radial symmetry to (1.3) for the 3D rotational flow. Theorem 5.1 To prove Theorems 5.1–5.3,we recall a lemma from [27]. Lemma 5.4 On the basis of Lemma 5.4,we obtain the following lemma: Because the proofs of Theorems 5.1–5.3 are similar to those of Theorems 2.1–2.3,we omit the details.By Corollary 5 of [27],we obtain the following corollary: Corollary 5.6 (1) if λ>0,the solutions exist globally; (2) if λ=0,and (2a) b≥0,the solutions exist globally; (2b) b<0,the solutions blow up in a finite time T; (3) if λ<0 and b≤0,the solutions blow up in a finite time T. In this article,we presented some special self-similar solutions for the model(1.3)of inviscid liquid-gas two-phase flow,and we classified the blowup phenomena or global existence of the solutions.The key point of this article has been the use of the explicit functions of the density and velocity for the equation of conservation of mass,which were discovered by Yuen,and choosing some special relations between the masses of gas and liquid. Model (1.3) is a simplified version of model (1.1).It is quite interesting to study the case in which the two phase velocities are different.What particular analytical solutions can we present for model (1.1)? This problem is worthy of further investigation.3 Elliptic Symmetry and Non-rotational Flow
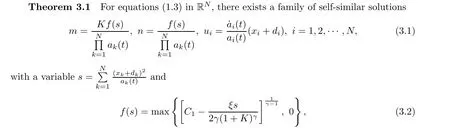


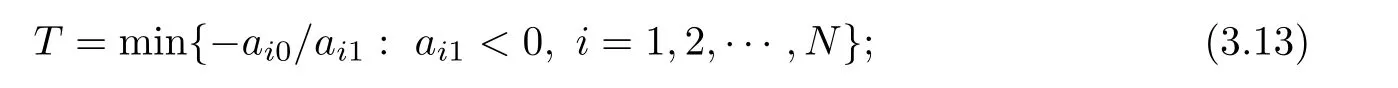
4 Radial Symmetry and 2D Rotational Flow




5 Radial Symmetry and 3D Rotational Flow




6 Conclusion and Discussion
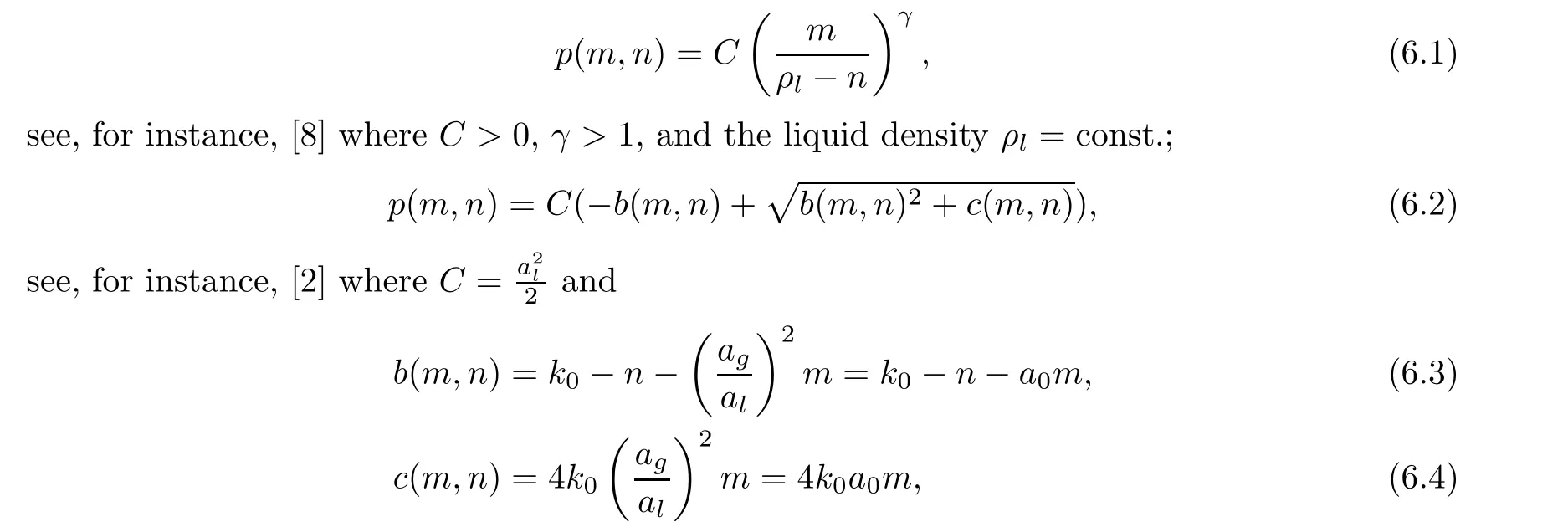

杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- CONTINUOUS DEPENDENCE ON DATA UNDER THE LIPSCHITZ METRIC FOR THE ROTATION-CAMASSA-HOLM EQUATION∗
- WEAK SOLUTION TO THE INCOMPRESSIBLE VISCOUS FLUID AND A THERMOELASTIC PLATE INTERACTION PROBLEM IN 3D∗
- ISOMORPHISMS OF VARIABLE HARDY SPACES ASSOCIATED WITH SCHRÖDINGER OPERATORS∗
- HITTING PROBABILITIES OF WEIGHTED POISSON PROCESSES WITH DIFFERENT INTENSITIES AND THEIR SUBORDINATIONS∗
- INHERITANCE OF DIVISIBILITY FORMS A LARGE SUBALGEBRA∗
- THE AVERAGE ABUNDANCE FUNCTION WITH MUTATION OF THE MULTI-PLAYER SNOWDRIFT EVOLUTIONARY GAME MODEL∗
