HITTING PROBABILITIES OF WEIGHTED POISSON PROCESSES WITH DIFFERENT INTENSITIES AND THEIR SUBORDINATIONS∗

Heng ZUO(左恒) Zhaohui SHEN(沈兆晖) Guanglin RANG(让光林),2

1.School of Mathematics and Statistics,Wuhan University,Wuhan,430072,China

2.Computational Science Hubei Key Laboratory,Wuhan University,Wuhan,430072,China E-mail:zuoheng@whu.edu.cn;shenzh@whu.edu.cn;glrang.math@whu.edu.cn

Abstract In this article,we study the hitting probabilities of weighted Poisson processes and their subordinated versions with different intensities.Furthermore,we simulate and analyze the asymptotic properties of the hitting probabilities in different weights and give an example in the case of subordination.

Key words weighted Poisson processes;hitting probabilities;subordination

1 Introduction

The Poisson process is one of the most important processes with stationary and independent increments.Its inter-arrival times are distributed exponentially.It is widely used in queueing theory,insurance andfinancial markets and earthquake modelling,among other things.

There are many generalizations of the Poisson process,such as the non-homogeneous Poisson process and the mixed Poisson process.For the last two decades,the fractional Poisson process caught the attention of researchers and a large amount of literature is available on this topic(see[8,9,11]).

The Poisson process of order n is a weighted sum of the independent Poisson processes,which was first introduced by Philippou(see[12,13]).It is defined as

where N(t),1≤j≤n are independent Poisson processes with the same intensity,λ.This is usually used to model the flow of clients in different services.In particular,insurance models generally use the Poisson process to model the arrival of claims that are limited to no more than one claim within a certain small time interval.However,the claim arrival in group insurance schemes may contain more than one claim.Kostadinova and Minkova(see[7])used process W(t) to model the claim arrival in groups of size n.Sometimes,the inter-arrival times may not be distributed exponentially,but distributed as Erlang(m,β) (see [6,10]).As a result,the process defined in [7]needs to be improved.

Subordination is a good way to generate new processes(see [3]).The subordinated process is a process whose time is replaced by a Lévy process which has non-decreasing sample paths.This Lévy process is called a subordinator.In recent years,the subordinated process has been extensively studied,and its good properties and connections to finance are explored in many articles and books (see [1,2,4,14]).

Sengar et al.(see [15]) considered the subordinated Poisson process of order n and studied its distributional properties,long-range dependence and limit theorems.Maheshwari et al.(see [16]) studied some extensions of process W(t) for different forms of the weights with the subordinated versions,and derived some formulas for the hitting probabilities of these processes.

In this article,we study two weighted Poisson processes of order n and a subordinated version with different intensities.They are defined as follows:

Our result is an extension of [16].We derive the distributions of the hitting times and the formulas of the hitting probabilities at level k for these three processes.Furthermore,since the explicit expressions are not available,we simulate and analyze the asymptotic properties of the hitting probabilities and their dependence on weighted functions,intensities and value n.

The rest of this article is organized as follows.In Section 2,we derive the formulas for the hitting probabilities of X(t) and Y(t).In Section 3,we simulate and analyze the asymptotic properties of these hitting probabilities.In Section 4,we derive the formula for the hitting probability of Z(t) and give an example.

2 Hitting Probabilities of Weighted Poisson Processes with Different Intensities

In this section,we study the hitting times and hitting probabilities of X(t)and Y(t).Define the hitting times at level k ≥1 by

2.1 Distribution of and hitting probability P(<∞)

Proposition 2.1

Let G(s) be the probability generating function (pgf) of X.Then

It is easy to obtain the distribution of X from G(s) as follows:

Now,we give the characterization of X(t) as a compound Poisson process.

Proposition 2.2

The process X(t) can be represented as a compound Poisson process,that is,

Proof

We calculate the probability generating function as follows:

Now,we turn to the main result of this subsection:the hitting probability of X(t).

Proof

(i) We first observe that when h>0,for ∀a>1,

Note that P(X(h)=m)=λh+o(h) for 1 ≤m ≤k ≤n,and P(X(h)=m)=o(h) for

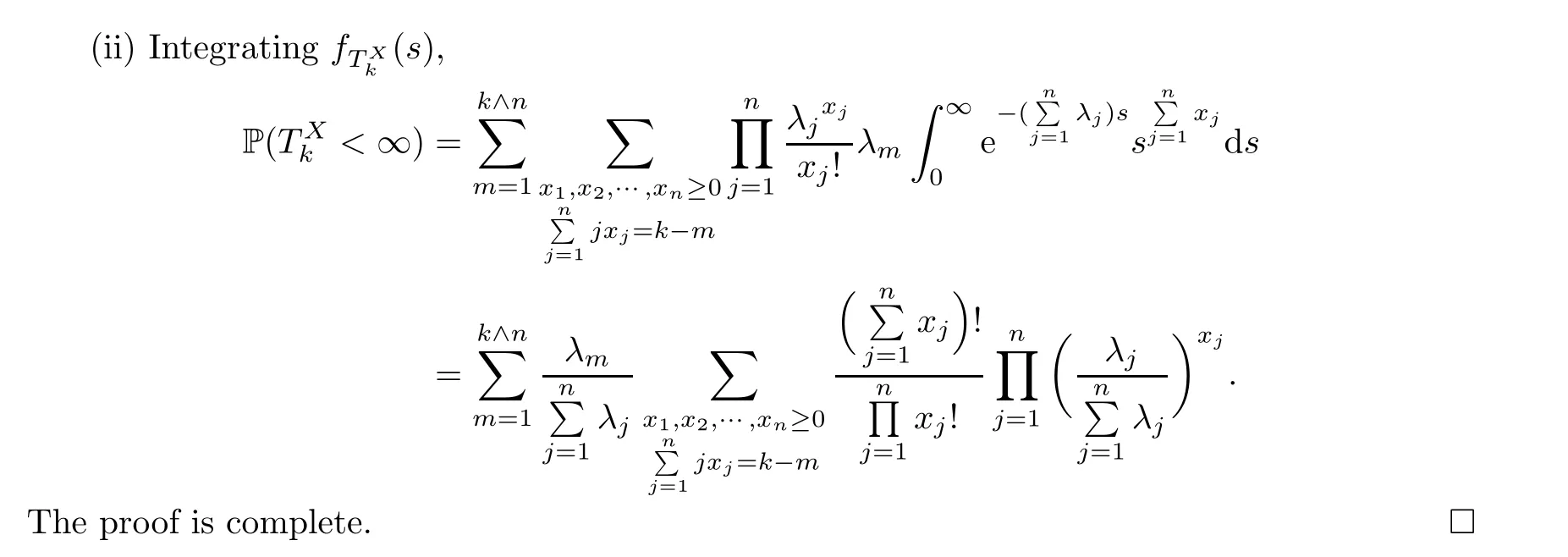
2.2 Distribution of and hitting probability P(<∞)

In this subsection,we consider the process Y(t),and extend the results in the previous subsection.Replacing j with g(j),we have

Proposition 2.5

Let G(s) be the probability generating function (pgf) of Y,so

By Proposition 2.5,we obtain

Equation (2.8) shows that Y(t) can only perform jumps up to size g(n) in a very short time interval.

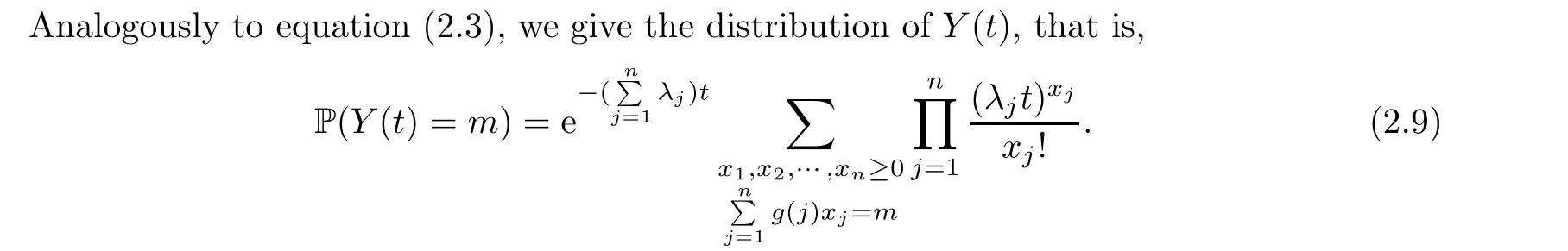
Now,we give the characterization of Y(t) as a compound Poisson process.

Proposition 2.6

The process Y(t) can also be represented as a compound Poisson process,that is,

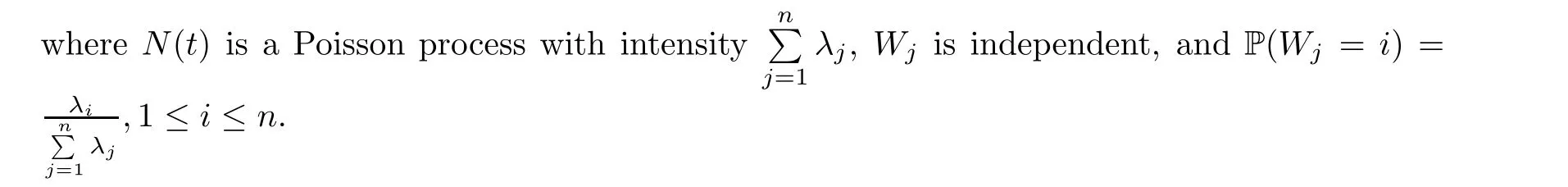
Now,we turn to the hitting probability of Y(t) and give the following theorem without proof:

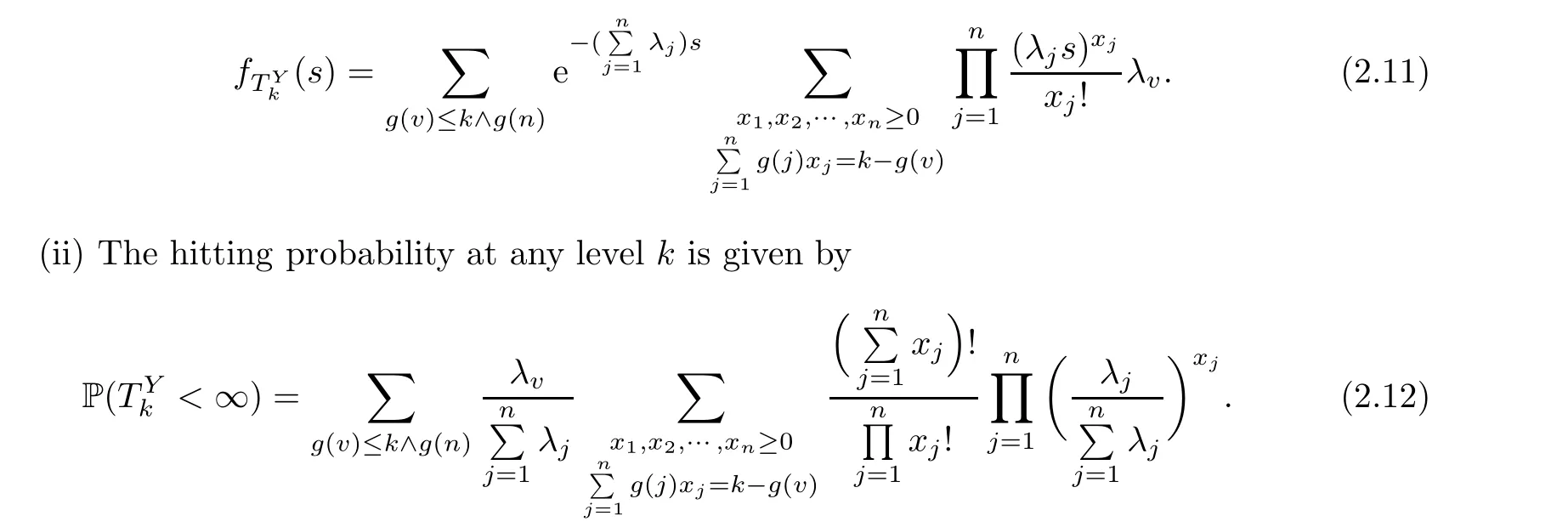
3 Simulation Results

Although equations(2.6)and(2.12)are very difficult to calculate explicitly,we can simulate and analyze their asymptotic properties.

3.1 Simulation results of P<∞)

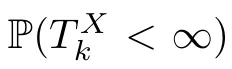
Table 1 Hitting probabilities of X(t) for n=2

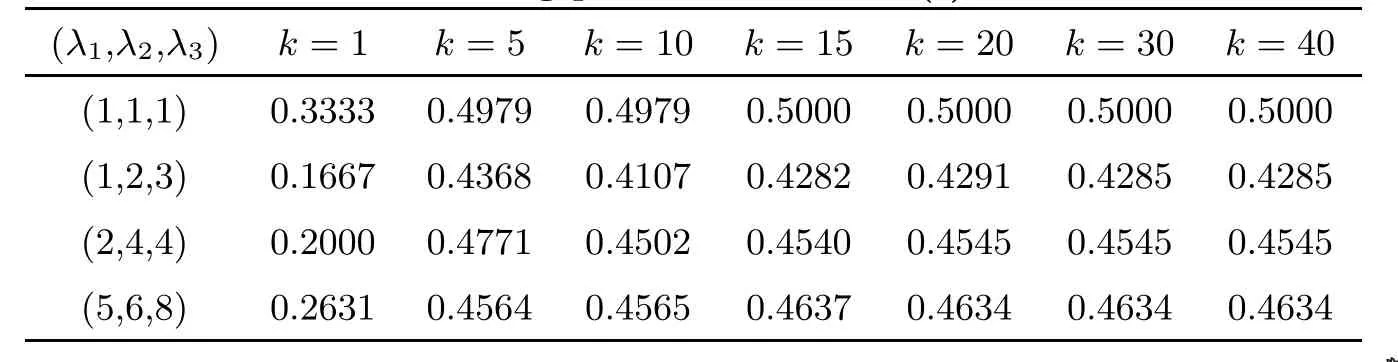
Table 2 Hitting probabilities of X(t) for n=3

Table 3 Hitting probabilities of X(t) for n=4

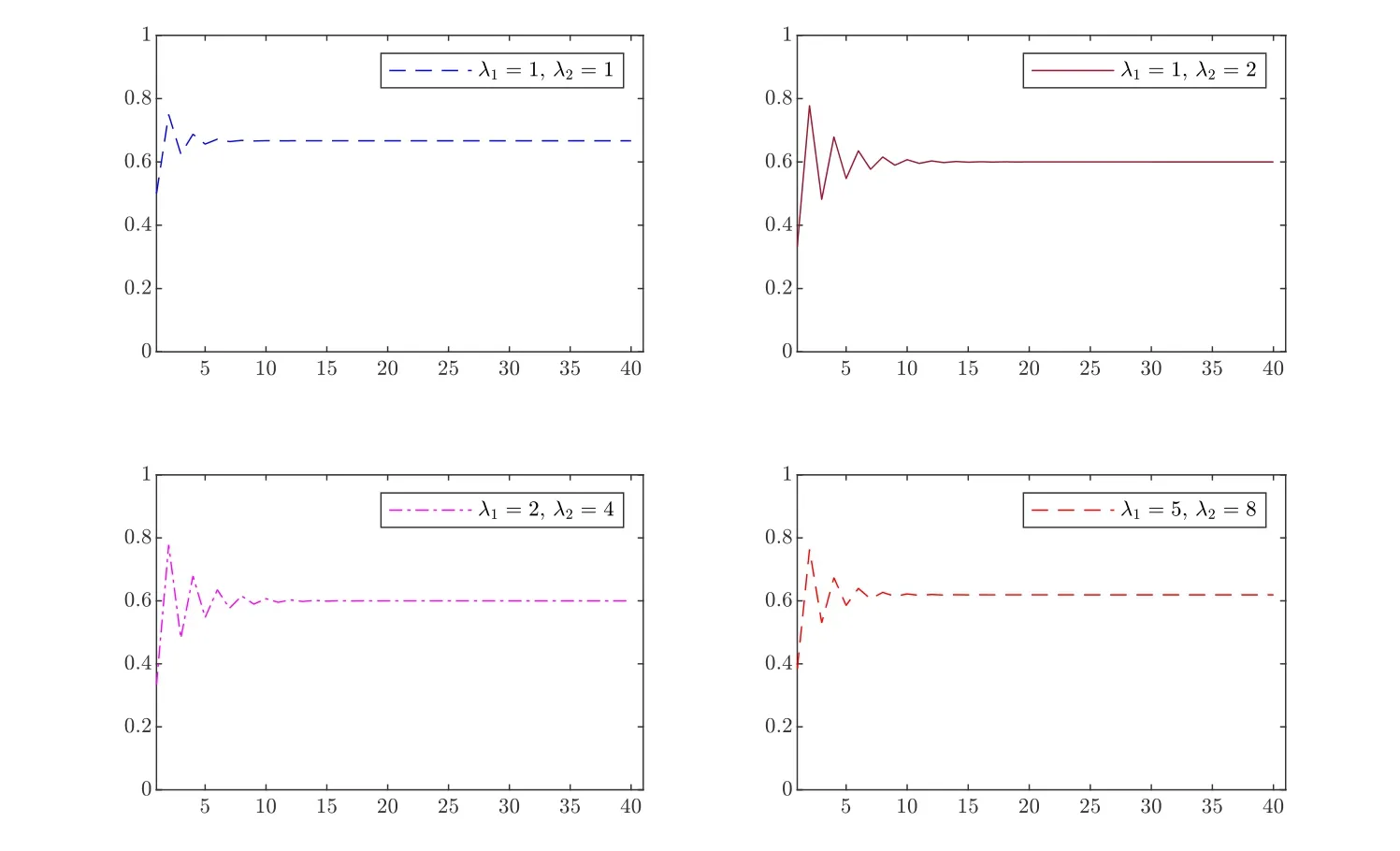
Figure 1 Hitting probabilities of X(t) for n=2

Figure 2 Hitting probabilities of X(t) for n=3

Figure 3 Hitting probabilities of X(t) for n=4

3.2 Simulation results of P(<∞)

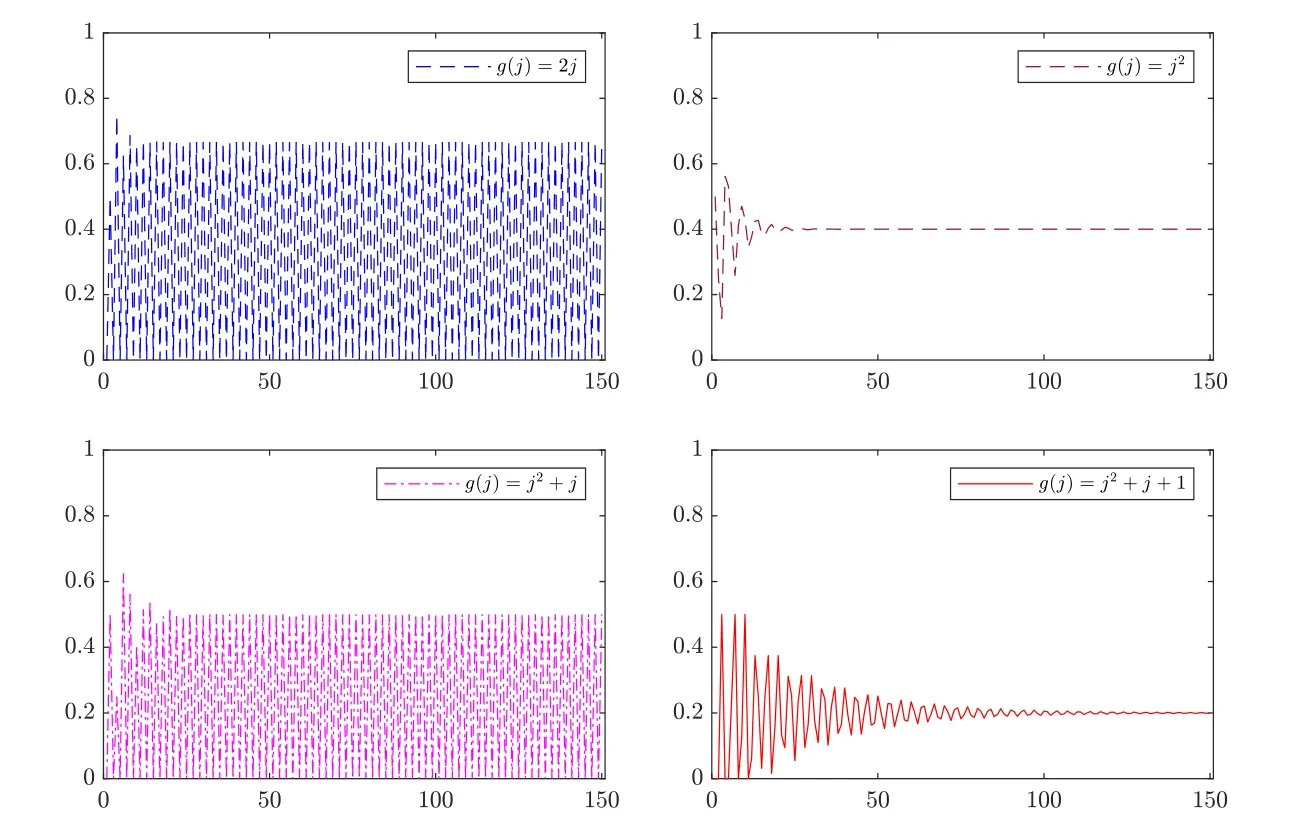
Figure 4 Hitting probabilities of Y(t) for (λ1,λ2)=(3,3)

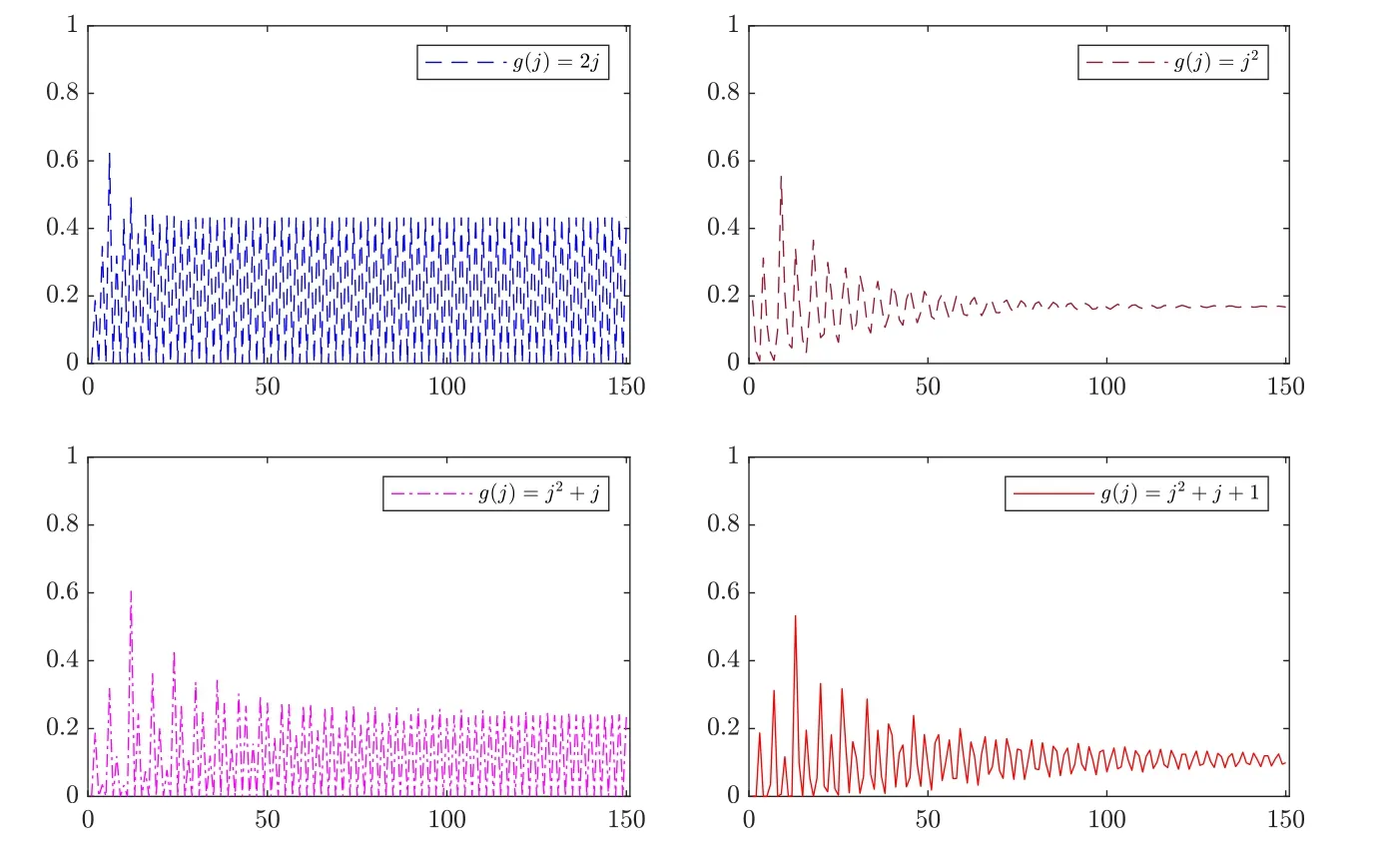
Figure 5 Hitting probabilities of Y(t) for (λ1,λ2,λ3)=(3,5,8)

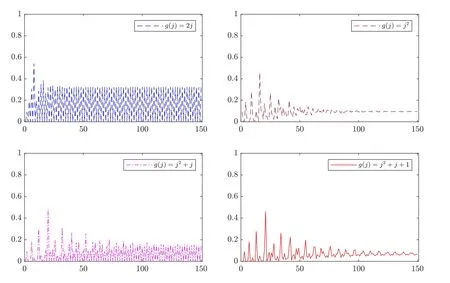
Figure 6 Hitting probabilities of Y(t) for (λ1,λ2,λ3,λ4)=(1,2,3,5)

Figure 7 Modified hitting probabilities of Y(t) for (λ1,λ2)=(3,3)

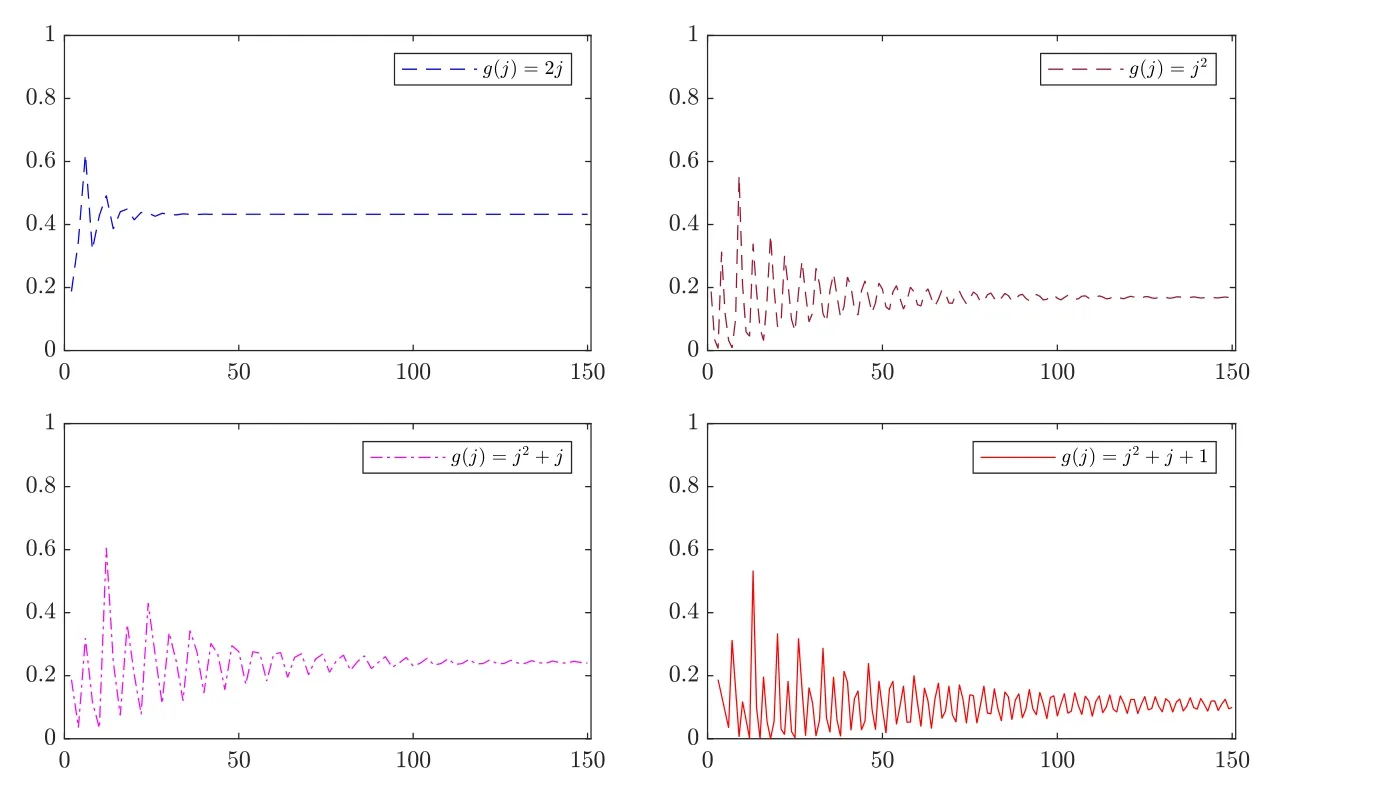
Figure 8 Modified hitting probabilities of Y(t) for (λ1,λ2,λ3)=(3,5,8)

Figure 9 Modified hitting probabilities of Y(t) for (λ1,λ2,λ3,λ4)=(1,2,3,5)

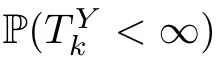
Table 4 Modified hitting probabilities of Y(t) for g(j)=2j

Table 5 Modified hitting probabilities of Y(t) for g(j)=j2

Table 6 Modified hitting probabilities of Y(t) for g(j)=j2+j

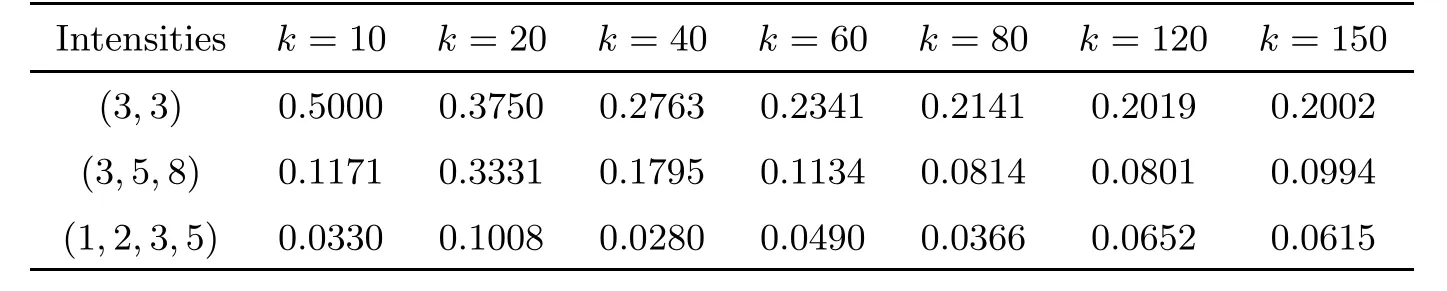
Table 7 Modified hitting probabilities of Y(t) for g(j)=j2+j +1

4 Subordinated Weighted Poisson Process with Different Intensities

In this section,we study the hitting time and hitting probability of process Z(t).Define the hitting time at level k ≥1 by

4.1 Probability density function of and hitting probability P<∞)

As in the previous section,we first calculate the probability generating function of Z(t).

Proposition 4.1

Let G(s) be the probability generating function (pgf) of Z,so

By Proposition 4.1 and the Taylor expansion of Ψ,we obtain

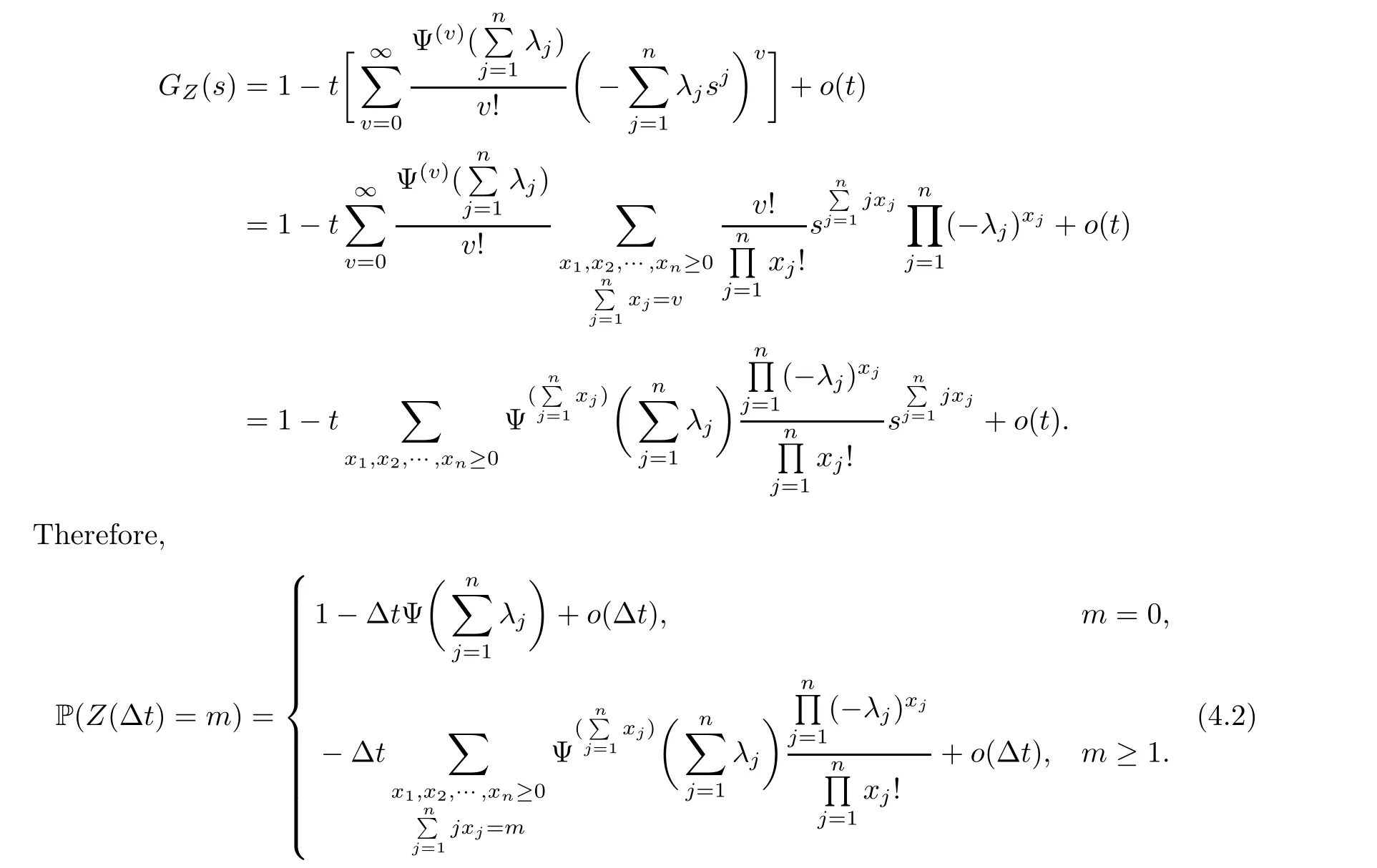
Unlike processes X(t) and Y(t),equation (4.2) shows that Z(t) can jump infinite times in a very short time interval.

Now,we give the characterization of Z(t) as a subordinated compound Poisson process.

Proposition 4.2

The process Z(t)can be represented as a subordinated compound Poisson process,that is,

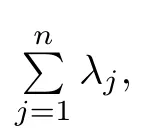
By taking the conditional expectation with respect to T(t),we obtain the distribution of Z(t) as follows:

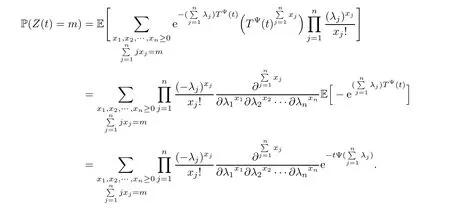
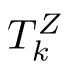
4.2 Example