THE AVERAGE ABUNDANCE FUNCTION WITH MUTATION OF THE MULTI-PLAYER SNOWDRIFT EVOLUTIONARY GAME MODEL∗

Ke XIA(夏可)

School of Economics,Zhengzhou University of Aeronautics,Zhengzhou 450000,China E-mail:xkforeducation@163.com

Xianjia WANG(王先甲)

School of Economics and Management,Wuhan University,Wuhan 430072,China E-mail:wangxj@whu.edu.cn

Abstract This article explores the characteristics of the average abundance function with mutation on the basis of the multi-player snowdrift evolutionary game model by analytical analysis and numerical simulation.The specific field of this research concerns the approximate expressions of the average abundance function with mutation on the basis of different levels of selection intensity and an analysis of the results of numerical simulation on the basis of the intuitive expression of the average abundance function.In addition,the biological background of this research lies in research on the effects of mutation,which is regarded as a biological concept and a disturbance to game behavior on the average abundance function.The mutation will make the evolutionary result get closer to the neutral drift state.It can be deduced that this affection is not only related to mutation,but also related to selection intensity and the gap between payoff and aspiration level.The main research findings contain four aspects.First,we have deduced the concrete expression of the expected payoff function.The asymptotic property and change trend of the expected payoff function has been basically obtained.In addition,the intuitive expression of the average abundance function with mutation has been obtained by taking the detailed balance condition as the point of penetration.It can be deduced that the effect of mutation is to make the average abundance function get close to 1/2.In addition,this affection is related to selection intensity and the gap.Secondly,the first-order Taylor expansion of the average abundance function has been deduced for when selection intensity is sufficiently small.The expression of the average abundance function with mutation can be simplified from a composite function to a linear function because of this Taylor expansion.This finding will play a significant role when analyzing the results of the numerical simulation.Thirdly,we have obtained the approximate expressions of the average abundance function corresponding to small and large selection intensity.The significance of the above approximate analysis lies in that we have grasped the basic characteristics of the effect of mutation.The effect is slight and can be neglected when mutation is very small.In addition,the effect begins to increase when mutation rises,and this effect will become more remarkable with the increase of selection intensity.Fourthly,we have explored the influences of parameters on the average abundance function with mutation through numerical simulation.In addition,the corresponding results have been explained on the basis of the expected payoff function.It can be deduced that the influences of parameters on the average abundance function with mutation will be slim when selection intensity is small.Moreover,the corresponding explanation is related to the first-order Taylor expansion.Furthermore,the influences will become notable when selection intensity is large.

Key words evolutionary game;average abundance function;mutation;stochastic process

1 Introduction

1.1 Aspiration rule

It is well known that the aspiration rule reflects the self-learning characteristics of individuals.More specifically,the evolutionary game behavior of individuals in a population is not on the basis of the difference between the payoff of different strategies,but on the difference between the payoff of strategy and aspiration level which reflects the concept of“satisfaction”in socio-economic issues.In general,the research on aspiration rules has focused on three aspects:(1)the study of the characteristics of average abundance after the introduction of various mechanisms;(2) the research on aspiration level as a function of parameters;(3) the comparative analysis of the aspiration rule and the imitation rule with different types of population as a background.

1.1.1 The study of the characteristics of average abundance after introducing various mechanisms

First,the WSLS mechanism is widely studied.The WSLS mechanism represents a winstay,lose-shift mechanism.More specifically,the individual will continue to adopt this strategy in this round if they are satisfied with the strategy of the previous round (the payoff of this strategy is higher than the aspiration level).Otherwise,other strategies will be adopted.Frederick A.Matsen [1]has proved that WSLS mechanism can greatly promote the improvement of average abundance.Xiaojie Chen [2]has proved that the random WSLS mechanism and local weight coefficient will contribute to the average abundance under appropriate conditions.Xiaojie Chen [3]has proved that the intermediate aspiration level can improve the average abundance.Yongkui Liu [4]has proved that the modified WSLS mechanism on the basis of the aspiration level will promote the average abundance and this effect has nothing to do with the initial distribution.Lei Zhou [5]investigated how heterogeneous aspiration based update functions will affect the evolutionary outcome.Jinming Du [6]has found that the effect of redistribution on cooperative promotion under different aspiration distributions varies with the proportion of redistribution.Matjaz Perc [7]has reviewed recent advances in the study of evolutionary dynamics of group interactions on top of structured populations,including lattices,complex networks and coevolutionary models.Attila Szolnoki [8]has found that a moderate fraction of cooperators can prevail even at very low multiplication factors if the critical mass is minimal.Attila Szolnoki [9]has reviewed experimental and theoretical research that advances our understanding of human cooperation,focusing on spatial pattern formation,on the spatiotemporal dynamics of observed solutions,and on self-organization that may either promote or hinder socially favorable states.

Secondly,many scholars are very concerned about the migration mechanism.It should be noted that this mechanism is only applicable to structured populations.Individuals can move to new locations under the influence of a migration mechanism.Hanxin Yang [10]has proved that the appropriate aspiration level will promote the migration of cooperative individuals,and that will lead to the formation of clusters and further promote the average abundance.Hai Lin[11]has proved that the migration of individuals with low aspiration level will help improve the average abundance.Yu Peng [12]has proved that the influence of the payoff of the betrayal strategy on average abundance can be ignored after the introduction of a migration mechanism.

In addition,the aspiration level will be affected by the payoff weight coefficient in the structured population,and this phenomenon has been widely investigated by researchers.Xiaojie Chen[13]has proved that the increase of the payoff weight coefficient will promote the average abundance.Weijun Zeng [14]has proved that the risk-adaptation mechanism on the basis of the aspiration level will maximize the average abundance.Jun Zhang [15]has proved that the aspiration level will have an oscillating effect on average abundance.Liu Y[16]has proved that the impact of aspiration level is non monotonic and the critical point needs to be considered in combination with other parameters.

1.1.2 The research on aspiration level as a function of parameters

The measurement of individual satisfaction will change with the evolution of time according to the research of economic sociologists.This means that the aspiration level is not fixed and needs to be considered as a function of the evolutionary time.The research in this area pertains to two situations.The first situation is to set the aspiration level of each stage as the weight of the corresponding coefficients of the previous stage.The second situation is to set the aspiration level as a function of the evolutionary time;this function has a disturbance coefficient.It is easy to deduce that the aspiration level is a random variable depending on the disturbance coefficient when the disturbance coefficient is not zero.This is similar to the first situation when the disturbance coefficient is zero.

Tadeusz Platkowski [17]has proved that the increase of population size will reduce the average abundance.He further proved [18]that the average abundance will be improved when considering multiple global aspiration levels.Roca CP [19]has proved that the average abundance will increase when greed is appropriately high,but that average abundance will decrease when greed is too high.Tadeusz Platkowski[20]has proved that the critical condition for maximizing the average abundance is independent of the initial distribution and group size when the aspiration level is appropriate.Xue Feng [21]has proved that the cost coefficients can have the effect that the aspiration rule on average abundance becomes bidirectional.Bin Wu [22]has proved that the evolutionary outcome with heterogeneous aspiration level is the same as that of the homogeneous one for regular networks under a weak selection limit.

Joe Yuichiro Wakano [23]has proved that the increase of the learning coefficient on the basis of aspiration level can promote the stability of average abundance.Changbing Tang[24]has proved that appropriate aspiration level will improve the average abundance when the cost-benefit ratio is at a critical value,and that critical value is related to the maximum Laplacian eigenvalue of the network.Zhixi Wu [25]has proved that the difference between synchronous and asynchronous updating will lead to different effects of the aspiration level on average abundance.Zhihai Rong [26]has proved that low aspiration level will promote the coexistence of different strategies and the appropriate aspiration level will promote the abundance of a generous strategy.

1.1.3 The comparative analysis of aspiration rule and imitation rule with different types of population as background

The comparison of the two rules has been widely concerned with different types of population as background,because there are some similarities between aspiration rules and imitation rules.Jinming Du [27]has proved that the effect of aspiration level on average abundance in a structured population under weak selection intensity is similar to that in a well-mixed population.Jinming Du[28]has also proved that compared with the imitation rule,the aspiration rule is more conducive to prolonging the duration of resource consumption.Zheng Wang [29]has proved that the evolutionary result under the aspiration rule will become highly robust when the corresponding coefficient is large enough.Haifeng Zhang[30]has proved that the role of the aspiration level lies in the negative feedback effect and promoting the heterogeneity distribution of node degree.Jinming Du [31]has derived the dominant condition for average abundance on the basis of weak selection intensity under the aspiration rule.Ming Li [32]has proved that high aspiration level will lead to the coexistence of different strategies and disappear,and that increase of the interaction coefficient will lead to the improvement of average abundance.Zhi Li[33]has proved that the combination of aspiration rules and a modified self questioning mechanism will lead to the increase of average abundance.Wei Chen[34]has proved that suboptimal selection on the basis of aspiration level will benefit the average abundance.Xuesong Liu [35]has proved that the combination of the aspiration rule and the imitation rule is conducive to the increase of average abundance.Kuangyi Xu [36]has proved that appropriate interaction coefficient and aspiration level will maximize the average abundance.

1.2 Mutation

Mutation is a biological concept which can be regarded as a disturbance to the original game behavior when it is applied to multi-player evolutionary dynamics.In addition,some new characteristics will appear in the evolutionary dynamics with mutation.It should be noted that game behaviors will become different from the previous situation when mutation is introduced into an evolutionary game.The most important point lies in the fact that the strategy updating of the focal individual will be disturbed by mutation.

It is usually assumed that mutation is small in evolutionary games.This assumption is related to the small probability of gene mutation.However,the probability of exploration(mutation) may be very high when considering the problem of the imitation dynamic,social learning or cultural evolution,and it may become an important and decisive factor in the result of system evolution.The size of mutation can lead to two situations:either random exploration represents a small disturbance to evolutionary dynamics (mutation is close to 0),or the evolutionary rule can only slightly affect the random selection process(mutation is close to 1).

In general,the research on the combination of mutation and an evolutionary game has focused on four aspects:(1) the effect of mutation on evolutionary fitness;(2) the effect of mutation on evolutionary dynamics;(3) the effect of mutation on the limit distribution and average abundance;(4)the effect of mutation on evolutionary game in the case of multi-strategy and mixed-strategy.

Regarding the first aspect,Martin Willensdorfer [37]has proved that the direction of mutation will affect evolutionary fitness and the increase of mutation will improve evolutionary fitness under certain conditions.

Regarding the second aspect,Anders Eriksson [38]has derived a new method for quickly calculating the fitness level by assuming a simple trigger strategy and multiple iterations of the game.On this basis,he has analyzed how the evolutionary dynamic depends on the following factors:mutation,group size,the value of payoff parameters and the structure of initial population.

Traulsen [39]has studied the evolution of stochastic differential equations.He has found that every type will appear in the population when mutation is large enough and the application of an approximate substitution of stochastic differential equations should be considered when mutation is small.

For the third aspect,Drew Fudenberg[40]has studied the Markov matrix corresponding to synchronous states and the algorithm of limit distribution on the basis of the evolutionary game under a combination of the imitation rule and mutation.Drew Fudenberg[41]has studied limit distribution on the basis of the classical Moran process under mutation.He has proved that the limit distribution will converge on a pure state,and every individual will adopt the same strategy in a pure state.Tibor Antal [42]has extended the strategy abundance dominance condition to the random birth-death process with arbitrary mutation and selection intensity.He has proved that the abundance of a cooperation strategy will be higher than the other in mutation-selection distribution when certain conditions are met.Bin Wu [43]has derived the critical value of mutation that makes the embedded Markov chain a good approximate result by calculating the difference between the actual stationary distribution and the approximate stationary distribution.He has compared the critical value of mutation for the coexistence game with the critical value of mutation for other games.

For the fourth aspect,Tibor Antal [44]has calculated the abundance of a pure strategy under weak selection and an arbitrary mutation in the case of multi-strategy.He has found the critical conditions of abundance dominance for low mutation and high mutation.It has been deduced that for arbitrary mutation,the corresponding critical condition is the linear weighting of the two conditions as mentioned earlier.Also,Tibor Antal[45]derived the critical conditions of abundance dominance for low mutation and high mutation in the case of a mixed-strategy.He deduced that for arbitrary mutation,the corresponding critical condition is the linear weighting of the two conditions,as mentioned earlier.It is easy to deduce that the result of this analysis in the case of a mixed-strategy is similar to that in the case of a multi-strategy.Dirk Helbing[46]has extended the traditional cooperative and betrayal strategies in the spatial public goods game to four strategies:cooperation,betrayal,cooperation with a punishment mechanism and betrayal with a punishment mechanism.It has been deduced that the spread of betrayers will be improved if mutation is frequent.Benjamin Allen[47]has studied the effects of graph topology and mutation on the evolutionary clustering in the population with a graph structure.It has been deduced that the aggregation of cooperators will be reduced and their evolutionary success will become more difficult if mutation is high.G.A.Kaiping [48]has studied the changes in an evolutionary result because of the alteration of the evolutionary updating rule in the case of multi-strategy and high mutation.It has been deduced that the alteration of the evolutionary updating rule will affect the topological structure of the equilibrium space if mutation is high.

It is widely accepted that individuals will not only have the characteristic of neutral drift,but also have the characteristic of mutation when mutation is introduced into an evolutionary game.This assumption will get closer to reality as the population size becomes larger.Many scholars have studied the evolutionary dynamics of the Moran process with a mutation or an imitation rule combined with mutation in previous studies.In this article,we will study the new characteristics of the average abundance function with mutation[49–56]on the basis of the classical multi-player snowdrift evolutionary game model driven by an aspiration rule [57–59].

1.3 The specific field and biological background of this research

It can be deduced through an analysis of previous research that many scholars focus on the characteristics of average abundance under the condition of selection intensity regarding the evolutionary game model with mutation.On the other hand,there is some room for improvement,for the theoretical basis of the corresponding data simulation results is not sufficient.Thus it can be seen that the approximate expression of the average abundance function under different levels of selection intensity deserves further discussion.Also,how to use the theoretical deduction of the average abundance function to explain the corresponding data simulation results is a field worth exploring.

It can be concluded that the specific field of this research is the approximate expression of the average abundance function under a different level of selection intensity ω and the use of the theoretical deduction on the basis of the intuitive expression of an average abundance function to explain the corresponding data simulation results.

The biological background of this research lies in the research on the effects of mutation,which is a biological concept and can be regarded as a disturbance to the original game behavior on the average abundance function which reflects the statistical characteristics of evolutionary results.The effect of mutation is to pull the average abundance function X(ω) to 1/2,no matter whether strategy A is favored by selection (X(ω) >1/2) or not (X(ω) <1/2).In other words,the mutation (in a biological sense) causes the evolutionary result to get closer to the neutral drift state at this time.To go a step further,this affection is related to three factors:mutation,selection intensity,and the gap between payoff and aspiration level.

1.4 Main work

The multi-player snowdrift evolutionary game model will be studied on the basis of the research on evolutionary game behaviors and expected payoff function.Then the transition probability equations with mutation will be established on the basis of the evolutionary dynamics with mutation.The expression of the average abundance function with mutation will then be deduced.The first order Taylor expansion of the average abundance function will be derived on the basis of this.Then the approximate expression of the average abundance function under different levels of selection intensity will taken into consideration.Finally,the influence of different parameters on the average abundance function will be studied.Generally speaking,the main work and contributions of this article are as follows:At first,the multiplayer evolutionary game behavior under mutation is analyzed and the intuitive expression of the average abundance function with mutation is given.Second,the basic characteristics of the average abundance function of the multi-player snowdrift evolutionary game model are studied in depth.The expression of the first order Taylor expansion of the average abundance function with mutation is given when the selection intensity is close to zero.The first order Taylor expansion will play an important role in the ensuing quantitative analysis of the simulation results of the average abundance function.Third,we make an approximate analysis of the average abundance function with mutation.The approximate formulas of the average abundance function corresponding to the multi-player snowdrift evolutionary game model are given on the basis of the characteristics of the expected payoff function π(i) and function h(i,ω),and the applicable scope of selection intensity ω is also given.Empirical formulas with a remarkable approximation result for average abundance function are obtained corresponding to small and large selection intensity.Fourth,the influence of multiple parameters on the average abundance function with mutation is calculated and analyzed by using a data simulation method on the basis of the multi-player snowdrift evolutionary game model.

2 Model

It should be noted that the game behaviors will become different from the common situation when mutation is introduced into the evolutionary game.The most important point here lies in the fact that the strategy updating of the focal individual will be disturbed by mutation.

Mutation represents the abnormal reproductive behavior of genes in terms of genetic concepts in biology,and its introduction into an evolutionary game brings new meaning to the game [60,61].More precisely,individuals are likely to make abnormal choices rather than be dominated by evolutionary rules.The theoretical expression of the average abundance function will become different under this influence.This means the influence of the corresponding parameters on the average abundance function should be reconsidered.In this section,the expression of the average abundance function with mutation will be deduced by analyzing the evolutionary dynamics under mutation.This will lay the theoretical foundation for further approximate analysis and data simulation.

2.1 The research on multi-player snowdrift evolutionary game model

2.1.1 The multi-player evolutionary game model

In a finite well-mixed population of size N,i is the number of A players.In this population,groups of size d are assembled randomly [62].The focal player can be of type A,or B,and encounter a group containing k other players of type A,to receive the pay-off aor b.The multi-player game payoff matrix [63–66]is as follows (see Table 1):

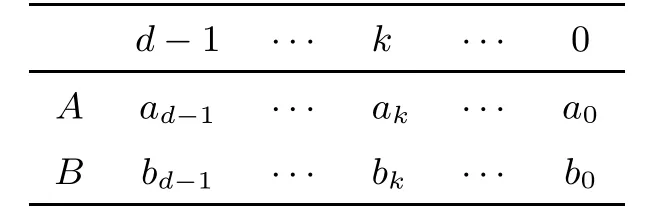
Table 1 The multi-player game payoff matrix

The expected payoff for any A,or B in a population of size N,with i players of type A and (N −i) players of type B,are given by π(i) and π(i).The general expression of expected payoff function π(i) and π(i) can be derived by using the probability theory and mathematical statistics on the basis of Table 1:

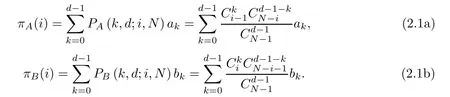
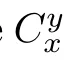
The corresponding extraction probability P(k,d;i,N)and P(k,d;i,N)will be the same for different kinds of multi-player evolutionary game models [67,68]because there is no difference in the game behaviors.It is remarkable that the difference lies in the expression of aand b.

The classical multi-player evolutionary game model is of these types:multi-player snowdrift evolutionary game model,multi-player linear public goods evolutionary game model,and multi-player threshold public goods evolutionary game model.Attila Szolnoki [69]has studied the evolution of cooperation in public goods games on the square lattice.He found that the promotion of cooperation due to spatial interactions is not rooted solely in having restricted connections among players,but also in individuals having the opportunity to collect payoffs separately from their direct opponents.Xiaojie Chen[70]has studied the evolution of cooperation in spatial public goods games with continuous strategies and has proved that in a structured population there exist intermediate values of both at which the collective contributions are maximal.

The multi-player snowdrift evolutionary game model [71–73]will be only taken into consideration due to the limited length of the article.The other two models will be considered in the future.

2.1.2 The multi-player snowdrift evolutionary game model

It should be noted that the multi-player snowdrift evolutionary game model [74–76]has been studied by many scholars.It is well known that the act of cooperation will provide a benefit b to all members of the group and the cost of cooperation c will be equally shared among cooperators.The expressions of the corresponding matrix elements aand bin table 1 can be easily deduced on the basis of the above discussions as follows:

2.1.3 The expected payoff function of the multi-player snowdrift evolutionary game model

In this section,the concrete expression of expected payoff function will be derived by inserting the expression of aand bfrom multi-player snowdrift evolutionary game model[71–73]into the formula (2.1) and making some simplification:

Proposition 2.1

The concrete expression of the expected payoff function of the multiplayer snowdrift evolutionary game model is as follows: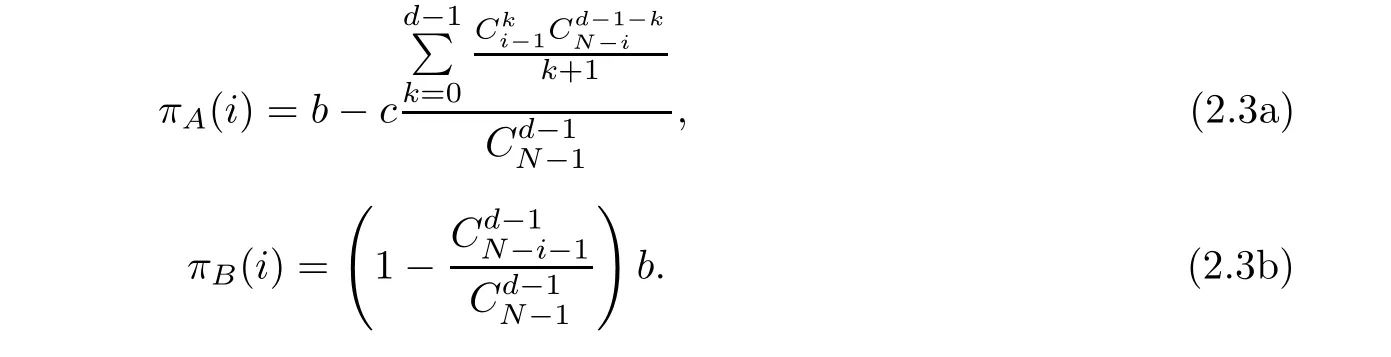

Proof

The expression of expected payoff function can be deduced by inserting the expression of aand binto formula (2.1):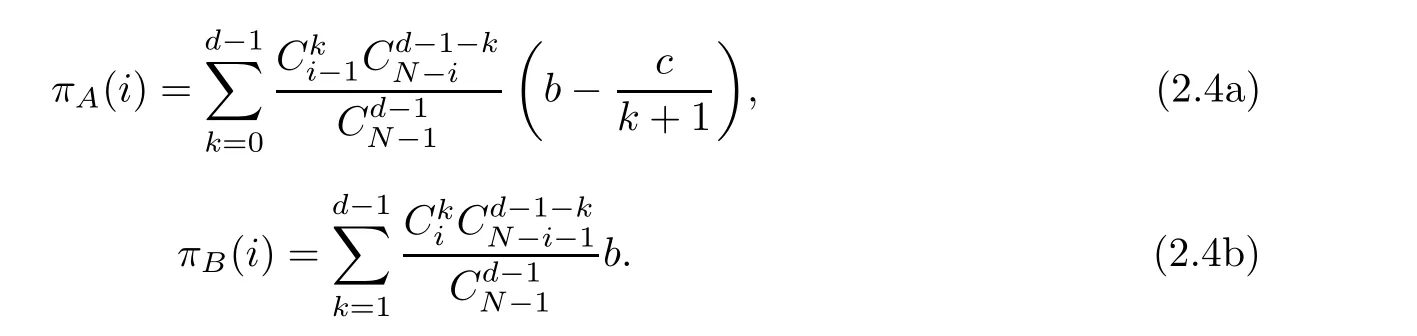

Formula (2.4a) can be rewritten by using the distributive law of multiplication:

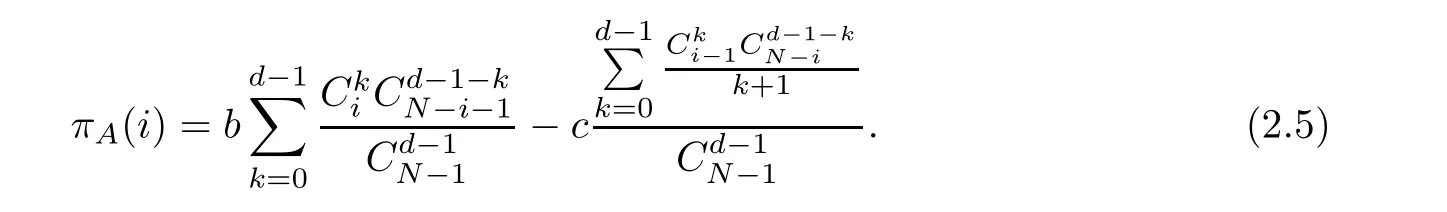
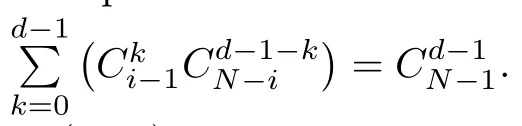
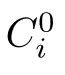
It can be deduced from formula (2.6) that mutation will not affect the payoff function and this property will be used in later analysis.It is easy to study the asymptotic property of the expected payoff function base on formula (2.3).It can be deduced that for π(i),the equation k=0 will hold when i →1.It will be seen from this that π(i)→b−c when i →1.In addition,the equation k=d −1 will hold when i →N.Thus it can be deduced that π(i) →b −c/d when i →N.In general,π(i)→b −c when i →1 and π(i)→b −c/d when i →N.

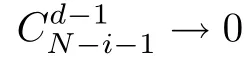
The change trend of the expected payoff function π(i)and π(i)with i has been basically grasped through the above analysis.We will draw the curves describing how π(i) (π(i) and π(i)) change with i (see Figure 1) for more intuitive and in-depth research.Here we choose the basic parameters:d=15,b=1.5,c=1,N=100.

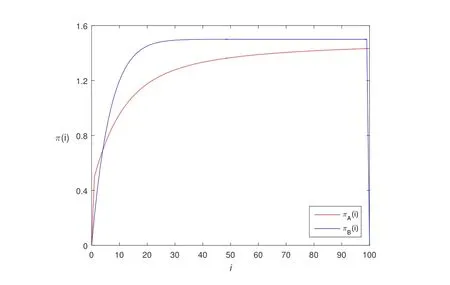
Figure 1 The expected payoff function πA(i) and πB(i)changes with i (d=15,b=1.5,c=1,N=100)

Two corollaries can be obtained from the analysis of Figure 1.

Corollary 2.1.3.1

The inequality π(i) >π(i) will hold when i is small (i <10).When i is not small (i ≥10),the inequality π(i) <π(i) will hold.In other words,the expected payoff for adopting strategy A will be larger than the expected payoff for adopting strategy B when the number of cooperators i is small.Conversely,the former will be smaller than the latter.It can be deduced from the above analysis that things will develop in the opposite direction when they become extreme in a multi-player snowdrift evolutionary game model.

Corollary 2.1.3.2

The expected payoff function π(i)and π(i)exhibits an asymptotic property when i>50.In other words,π(i) tends to be stable with respect to i when i>50.

We not only have a deeper understanding of the relationship between π(i) and i,but have also laid a foundation for the analysis of the characteristics of the average abundance function with mutation in the next section through the analysis of the concrete expression of the expected payoff function.

2.2 The research on average abundance function with mutation

2.2.1 Game behaviors of aspiration dynamics with mutation

It should be noted that both the aspiration rule and mutation are not active behaviors,but in essence the intrinsic characteristics of individuals.Therefore,the evolutionary game with the characteristics of the aspiration rule and mutation will become different from the strategy selection.The most noteworthy point is that the game behaviors of individuals will be disturbed by mutation.

When mutation is introduced into an evolutionary game,the game behavior [77–79]will become different from the previous situation.More specifically,an individual X (focal individual) will be selected randomly from the individuals in the population and at the same time(d −1) individuals will be selected randomly from the rest simultaneously in each game.It can easily be seen that a group of size d will emerge [80,81].The d individuals two strategy stochastic game model comes into being on the basis of this.

It should be noted that the individuals will not only be driven by aspiration rule [82,83],but also be disturbed by δ (mutation).Figure 2 is the diagram of multi-player evolutionary dynamic under mutation and an aspiration rule.And one corollary can be obtained from the analysis of it.

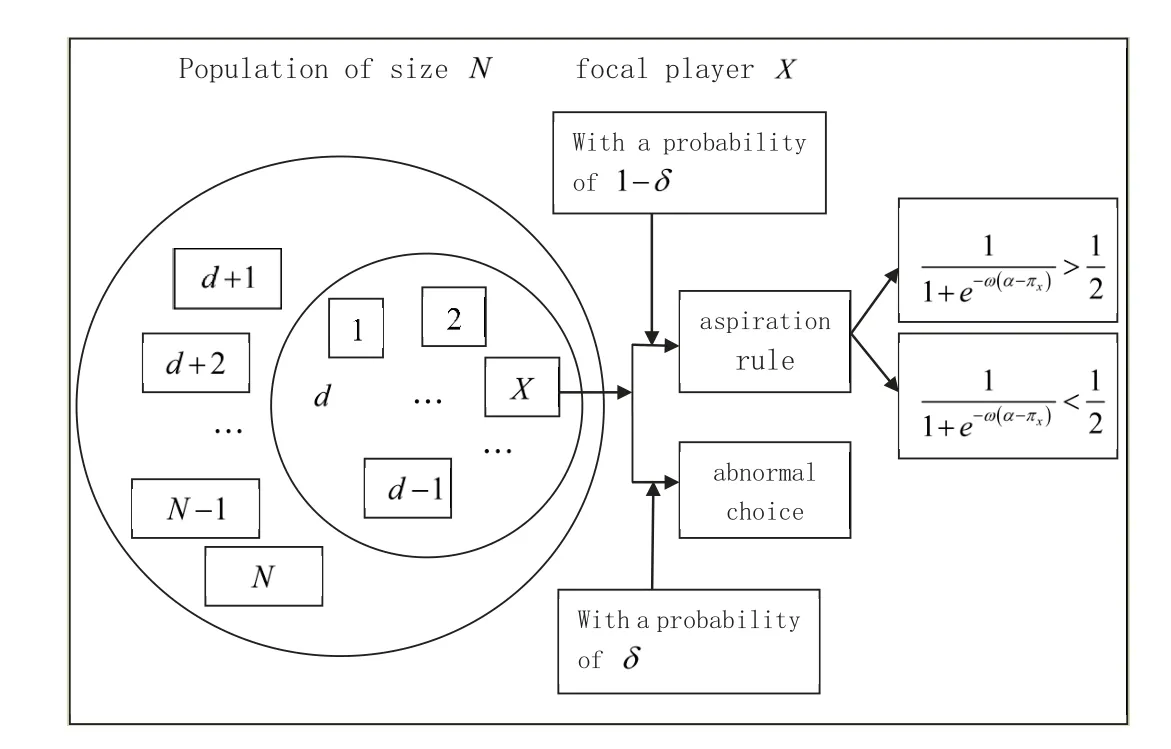
Figure 2 The diagram of a multi-player evolutionary dynamic with mutation

Corollary 2.2.1

There are two orientations.One is the evolutionary game on the basis of probability (1 −δ) and this is guided by the aspiration rule.The other is mutation on the basis of probability δ and this is guided by mutation.In fact,either the evolution occurs on the basis of the aspiration rule or mutation occurs at each moment.It is easy to deduce that each situation may happen and the sum of the two probabilities is 1.

The transition probability equation of the evolutionary process with mutation [84]can be deduced on the basis of Figure 2 and the above analysis as follows:

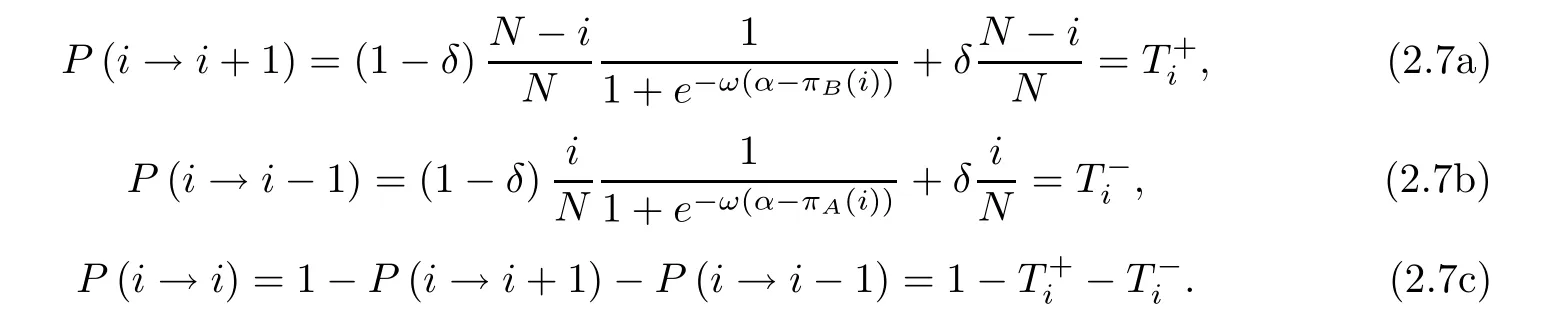
Here,ω represents selection intensity and α represents the aspiration level,which reflects the satisfaction of individuals in the formula (2.7).It can be deduced from formula (2.7) that the evolutionary process will degenerate into the situation of no mutation when δ=0.

On the other hand,the individuals will be completely dominated by mutation when δ=1.The proportion of individuals adopting strategy A and the proportion of individuals adopting strategy B will tend to be the same in this circumstance.In other words,each proportion will be 1/2.

It can be seen from the above analysis that a new motivation is added to the evolutionary process besides the aspiration rule [85–87],because of the introduction of mutation.

2.2.2 The characteristics of average abundance function with mutation

It is well known that the statistical characteristics of evolutionary process can be analyzed on the basis of the average abundance function X(ω).In other words,formula (2.8) reflects the statistical properties of the evolutionary process.

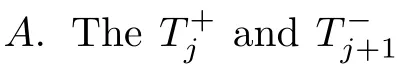
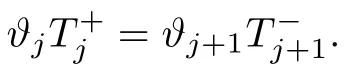
Proposition 2.2

The intuitive expression of the average abundance function of strategy A is as follows when the transition probability equation of evolutionary state is defined by formula (2.7):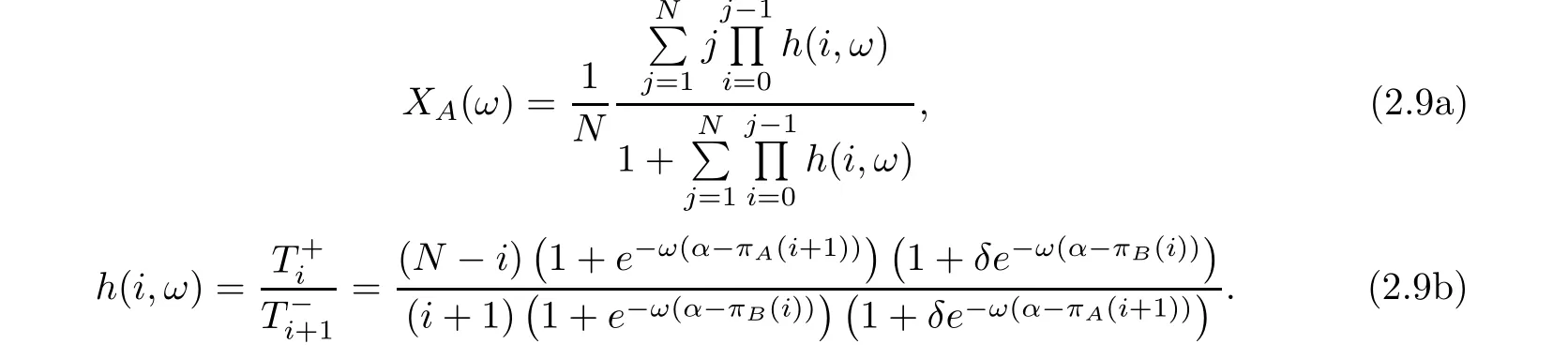

The expression of π(i+1)and π(i)in formula(2.9b)can be easily obtained on the basis of formula (2.1):

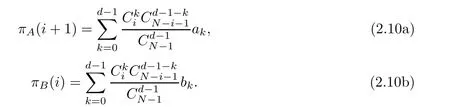
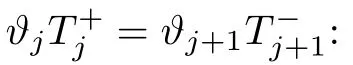
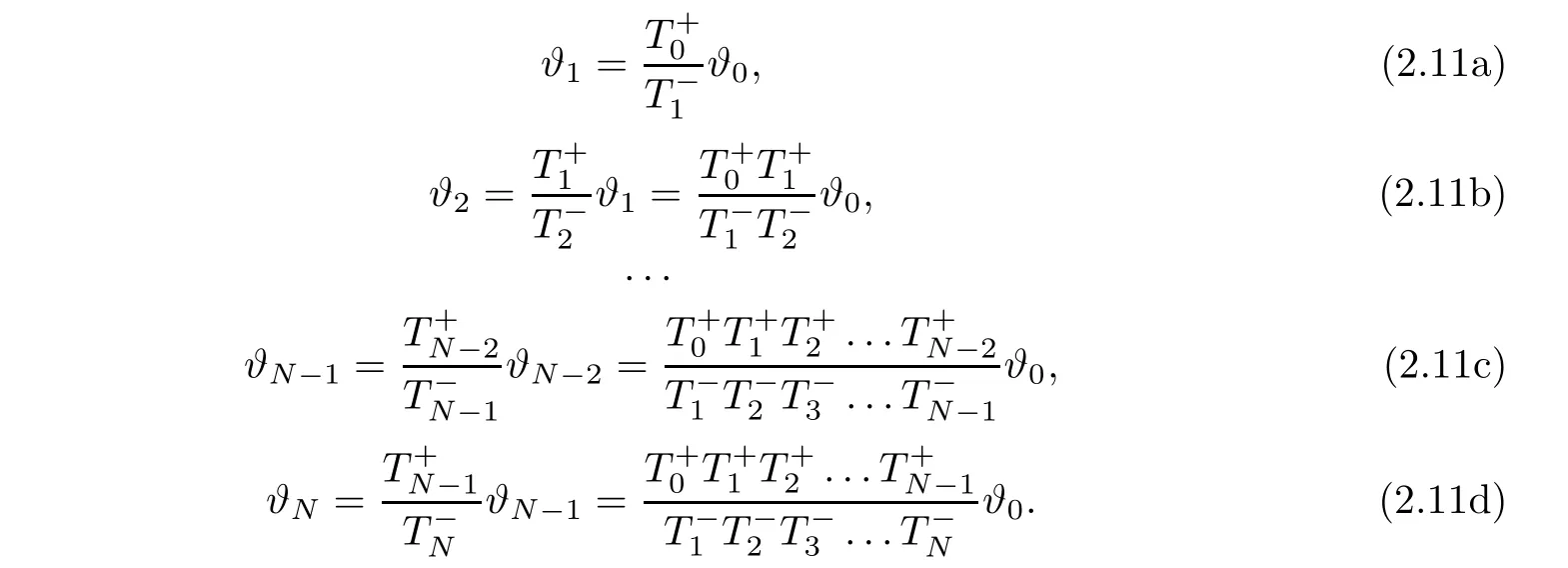
Obviously,the general expression of the above formula is

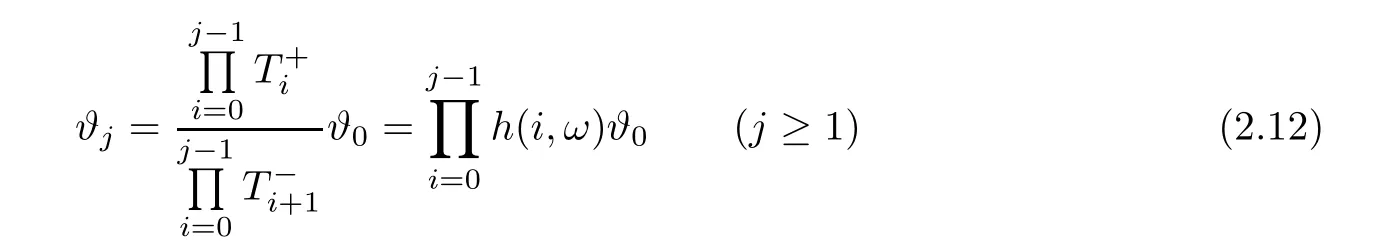
The expression of the average abundance function X(ω)can be further rewritten as follows,by inserting formula (2.16) into formula (2.8):

Obviously,compared with formula (2.8),formula (2.9) reflects the intuitive relationship between the average abundance function and selection intensity ω,the aspiration level α and other relevant items such as N,d,a,b.Therefore,the formula (2.9) lays the foundation for further analysis and numerical simulation.

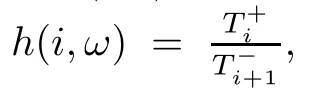
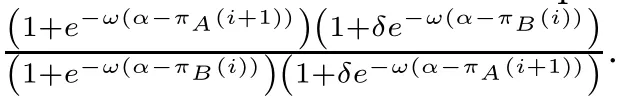
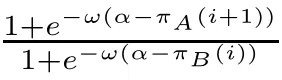
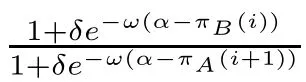
An interesting phenomenon can be found when comparing the third part with the second part.When δ=1,the function h(i,ω) will only be determined by the first part and the corresponding average abundance function will be X(ω)=1/2,because mutation and the aspiration rule completely offset each other.On the other hand,the effect of mutation will completely disappear and the aspiration rule will govern the evolutionary process when δ=0.

In other cases (0 <δ <1),the role of the second part will partial offset the role of the third part.This partial offset is reflected.If the following formula holds:

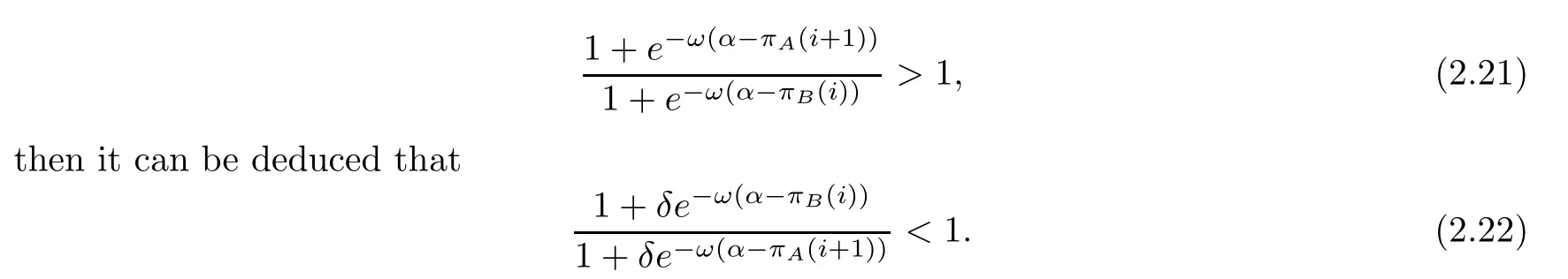
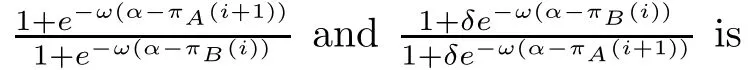
3 Results and Discussions

3.1 Analytical analysis of the average abundance function with mutation

3.1.1 The first-order Taylor expansion of the average abundance function with mutation

The average abundance function is an important tool for evaluating the results of evolutionary game from the perspective of an evolutionary game.The average abundance function is a compound function with many parameters,and its complexity will be further enhanced because of the introduction of mutation.

This section will focus on the influence of the Taylor expansion on the average abundance function with mutation defined by formula(2.9).The Taylor expansion acts on the basis of the continuity of the average abundance function with respect to selection intensity ω.

The common method is to use the first order Taylor expansion of the stationary distribution to get the Taylor expansion of the average abundance function,however,the average abundance function will be expanded directly by Taylor expansion in this section.Some related operations will be simplified and a new expansion method will be obtained in this way.

Proposition 3.1

The average abundance function given by formula (2.9) has good continuity with respect to selection intensity ω when ω is sufficiently small.Therefore,the first order Taylor expansion of the average abundance function X(ω) with mutation is as follows: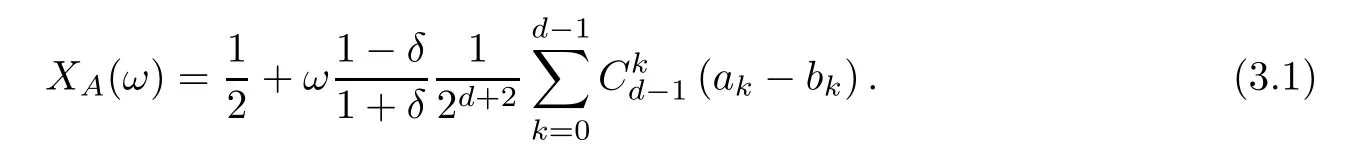

Proof

The Taylor expansion of the average abundance function X(ω) can be easily obtained when ω is sufficiently small (ω →0):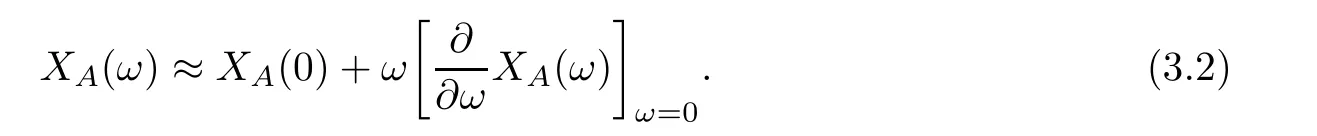

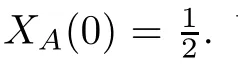
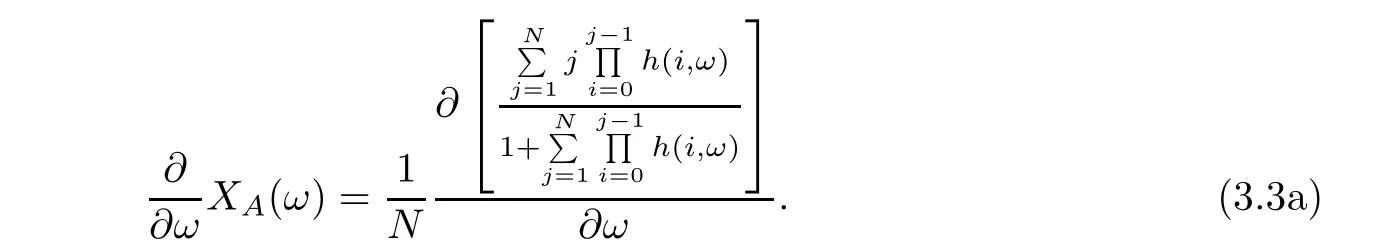
In order to simplify the operations,we set:

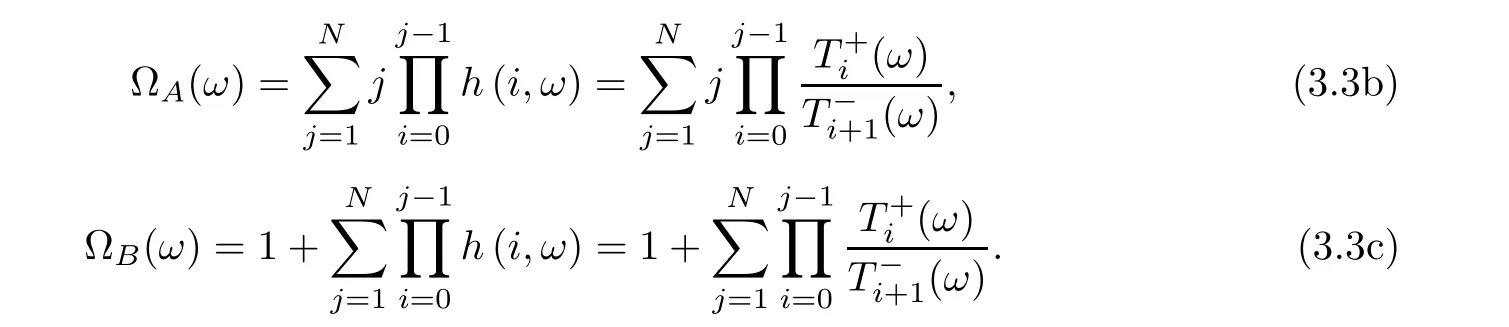
It can be deduced by inserting equations (3.3b) and (3.3c) into equation (3.3a) that:

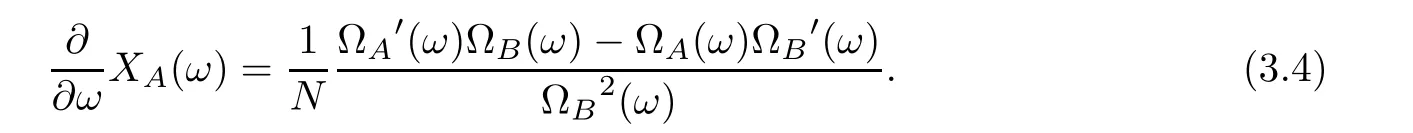
It can be obtained by substituting formulas (3.10)–(3.12) into formula (3.4) that

By performing some complicated operations on formula (3.13) (see Appendix A),it can be obtained that

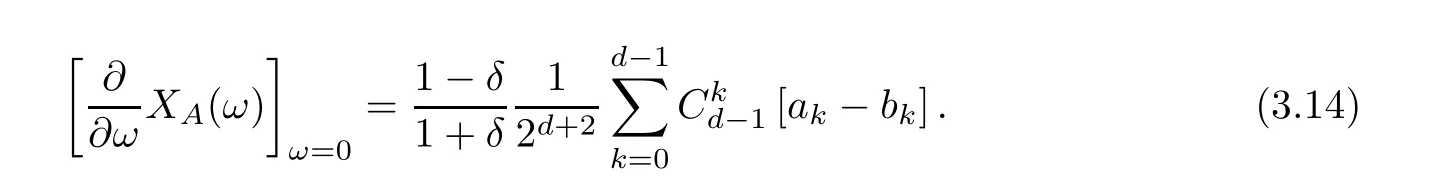
Four corollaries describing the basic properties of the average abundance function X(ω)when ω →0 can be obtained by comparing formula (3.1) with formula (2.9).

Corollary 3.1.1.1

Formula (3.1) is only related to d and has nothing to do with N.This means that the statistical significance of the average abundance function becomes weaker when ω →0.

Corollary 3.1.1.2

Formula(3.1)is independent of aspiration level α.It can be deduced from this that the role of the aspiration level will disappear when ω →0.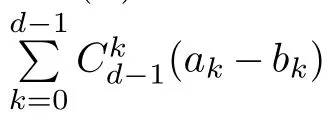

Formula (3.1) is the simplest form of the average abundance function under the condition of weak selection intensity.In addition,this formula will play a significant role when analyzing the results of the numerical simulation in Section 3.2.

3.1.2 The approximate expression of the average abundance function with mutation

In this section,the approximate theory will be used to analyze the average abundance function with mutation on the basis of the multi-player snowdrift evolutionary game model[91,92].Then the approximate expression of the average abundance function under different level of selection intensity ω can be deduced.

First,formula (2.9b) can be rewritten as follows:

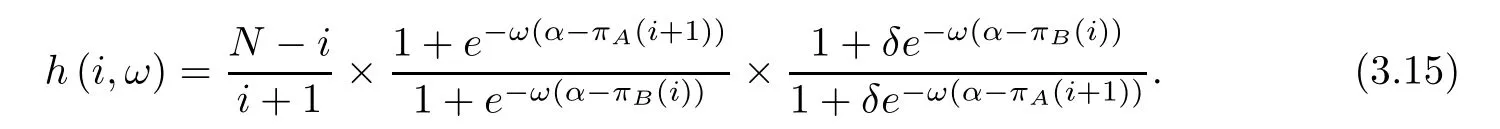
The expected payoff function π(i),π(i)of the multi-player snowdrift evolutionary game model has been analyzed in section 2.1.3.It can be seen from Figure1 that the expected payoff functions π(·) will tend to be stable with respect to i when i is large.

It can be deduced that the items inside the brackets in the exponential terms of equation(3.15) will change slowly.In other words,the α −π(·) will change slowly.It can be seen from this that the exponential terms will mainly change with selection intensity ω.In other words,ewill mainly change with selection intensity ω.

It can be seen from the above discussions that when selection intensity ω increases gradually and mutation is small(δ ≪1),the exponential terms in equation(3.15)will satisfy the inequality

Therefore,the last item on the right hand side of formula (3.15) can be expanded by power series.The power series expansion is as follows:

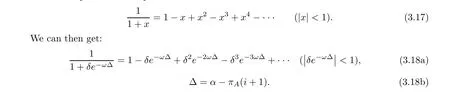
It can be deduced by retaining the linear term on the right side of formula (3.18a) and substituting it into formula (2.9b) that

It should be noted that formula(3.20)is applicable only when selection intensity ω is small.The range of selection intensity ω can be determined according to the empirical formula:

It can easily be deduced that the selection intensity ω cannot be large when the average abundance function is calculated on the basis of the h(i,ω) in formula (3.20).This means that in the next step,the condition that selection intensity ω is large should be taken into consideration.If selection intensity ω continues to increase and makes the condition (3.16)unsatisfied,we will get that:

Because mutation is small (δ ≪1),the following inequality will hold:

On the basis of formula (3.23),the second term on the right side of formula (3.15) can be approximated as

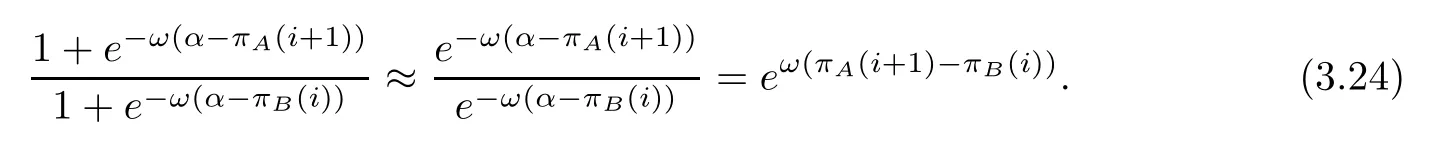
By substituting formula (3.24) into formula (3.15),it can be deduced that

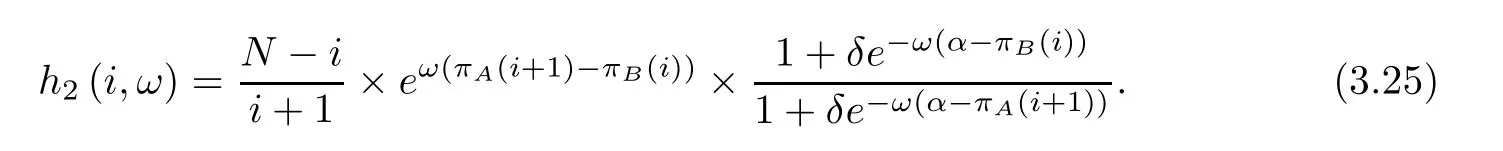
It should be noted that formula (3.25) is applicable only when selection intensity ω is large.The range of selection intensity ω can be determined according to the following empirical formula:

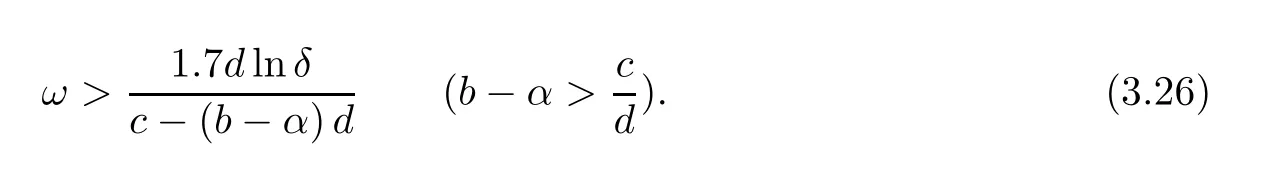
The following proposition can be obtained on the basis of the above discussions:

Proposition 3.2

For the multi-player snowdrift evolutionary game model with mutation,we have found

(1) When selection intensity ω is small,the approximate expression of the average abundance function with mutation will be as follows:

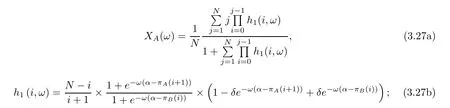
(2)When selection intensity ω is large,the approximate expression of the average abundance function with mutation will be as follows:

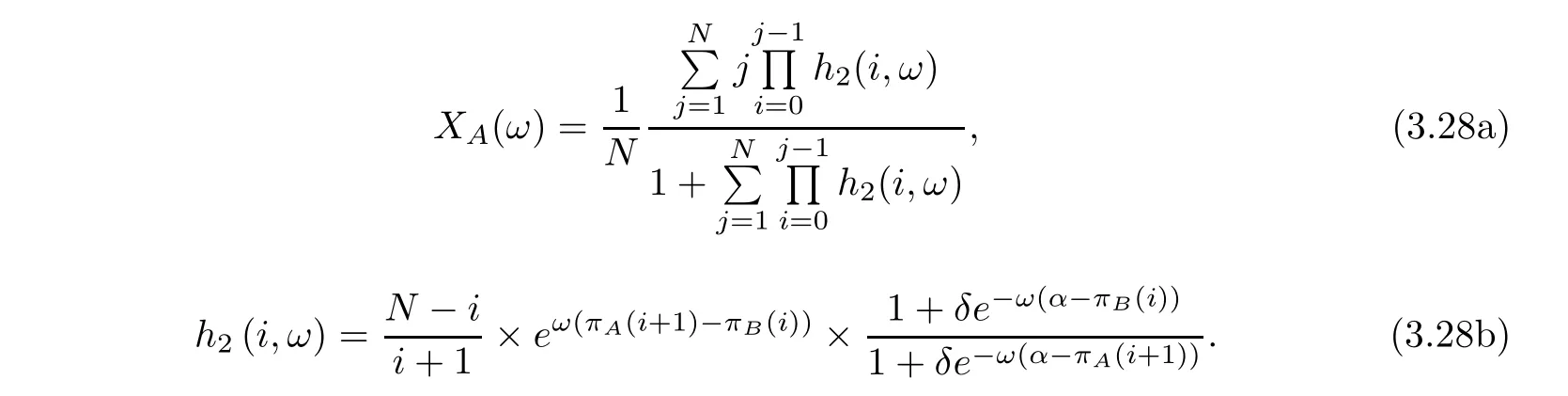
Then we plot the curves describing how the average abundance function X(ω) changes with selection intensity ω under different mutation δ (Figure 3),in order to verify proposition 3-2.It should be noted that the curves in the Figure 3 are on the basis of different formulas.The red line is the average abundance function X(ω)on the basis of the approximate formula(3.27).The black line is the original average abundance function X(ω)on the basis of formula(2.9),which contains no approximation.The blue line is the average abundance function X(ω)on the basis of the approximate formula (3.28).

Two corollaries can be obtained from the analysis of Figure 3.

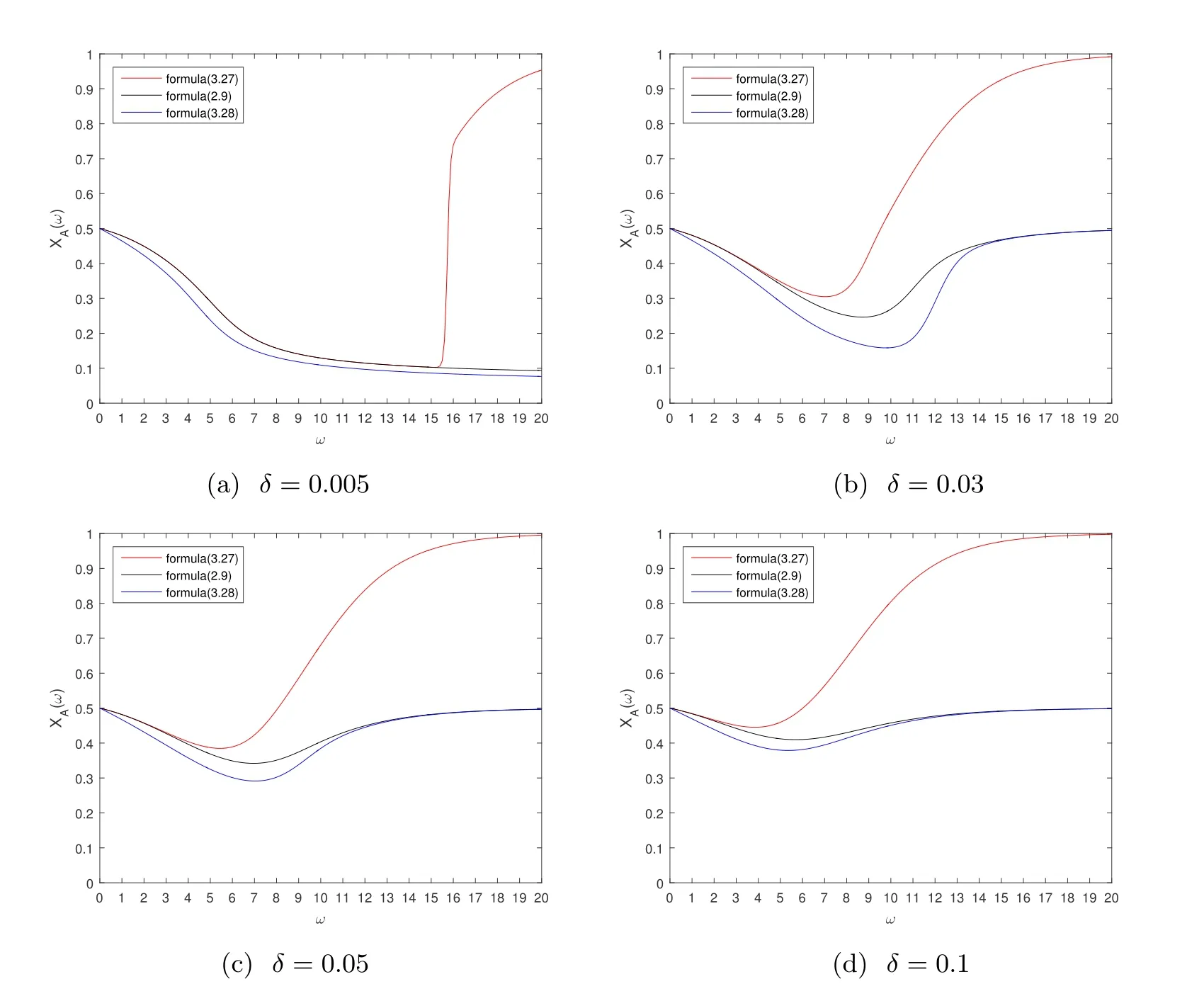
Figure 3 The average abundance function XA(ω) with mutation on the basis of different formulas(d=15,b=1.5,c=1,α=1,N=100)

Corollary 3.1.2.1

The three curves on the basis of different formulas are close to each other when mutation δ is very small.This indicates that the effect of mutation on the average abundance function is negligible when mutation is very small.

Corollary 3.1.2.2

The effect of mutation on the average abundance function begins to increase when mutation δ raises.This increase will be reflected in the application scope of formula(3.27)and formula(3.28).The application scope of formula(3.28)becomes wider with the growth of mutation δ.

The significance of the above approximate analysis lies in that we have grasped the basic characteristics of the influence of mutation on the average abundance function of the multiplayer snowdrift evolutionary game model theoretically:

(1) When mutation δ is very small,the influence is slight and can be neglected;

(2) When mutation δ rises,the influence begins to increase and this influence becomes more remarkable with the increase of selection intensity ω.

3.1.3 Inferences

We have obtained the approximate expressions of the average abundance function with mutation under different levels of selection intensity ω through the analytical analysis on average abundance function.The following inferences are obtained:

Inference 3.1.1

The first order Taylor expansion of the average abundance function X(ω) with mutation is defined as formula (3.1) when selection intensity ω →0.

Inference 3.1.2

The approximate expression of the average abundance function with mutation is defined as formula (3.27) when selection intensity ω is small.The approximate expression is defined as formula (3.28) when selection intensity ω is large.

3.2 Numerical simulation on the average abundance function with mutation

It can be seen from the above discussions that different parameters will have different effects on the average abundance function with mutation.This is a problem worthy of discussion.By numerical simulation and analytical comparison,we can further explore the influence of parameters on the average abundance function with mutation on the basis of the multi-player snowdrift evolutionary game model [93–95].The research on this disturbance will help us understand the effect of mutation [96]on the average abundance function more deeply.

We will consider the specific value of parameters.It can be deduced that the third term on the right side of function h(i,ω),defined by formula (3.15),will degenerate to 1 if mutation is too small.On the other hand,the effect of mutation will become too dominant if mutation is too large.Because of the above reasons,we set mutation δ=0.03.Finally,the basic parameters are set as d=15,b=1.5,c=1,α=1,N=100,δ=0.03.

It should be noted that we will study the trend of the average abundance function when d,b,c and α change.This means that when we analyze the effect of a particular parameter(such as d),the other parameters (b,c,α) will remain unchanged.Other analyses are similar.Then the value of the average abundance function will be calculated by substituting the above parameters into formula (2.9),and the curves describing how the average abundance function changes with parameters will be obtained.

3.2.1 The influence of d on the average abundance function with mutation

Figure 4 describes how the average abundance function with mutation changes with the size of group d.Two corollaries can be obtained from the analysis of Figure 4.

Figure 4 The average abundance function XA(ω) with mutation changes with d in a multi-player snowdrift evolutionary game model (b=1.5,c=1,α=1,N=100,δ=0.03)

Corollary 3.2.1.1

The average abundance function with mutation changes with d very slowly when ω=0.5.

Corollary 3.2.1.2

When ω=4 and ω=9,the average abundance function with mutation will increase and get close to 1/2 if d>12 .

To explain the first corollary,formula (2.2)will be substituted into formula(3.1) and some simplifications will be made (see Appendix B).Then it can be deduced that

It can be deduced that the formula (3.29) can be simplified when d is large

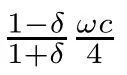
The reason for the second corollary is that many individuals will choose strategy B under the influence of the aspiration rule when selection intensity ω is large.On the other hand,a lot of individuals who choose strategy B will turn to choose strategy A because of the effect of mutation.Therefore,the synthesis of the above two influences will make the proportion of individuals choosing strategy A and the proportion of individuals choosing strategy B reach a new equilibrium,that is something,close to 1/2.Thus the average abundance function will get close to 1/2 when d increases to a very high level.

3.2.2 The influence of b on the average abundance function with mutation

Figure 5 describes how the average abundance function with mutation changes benefit b.Two corollaries can be obtained from the analysis of Figure 5.

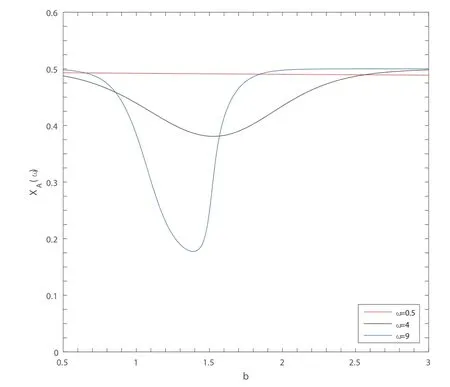
Figure 5 The average abundance function XA(ω) with mutation changes with b in a multi-player snowdrift evolutionary game model (d=15,c=1,α=1,N=100,δ=0.03)

Corollary 3.2.2.1

The average abundance function with mutation will basically remain unchanged with the increase of b when ω=0.5.

Corollary 3.2.2.2

The average abundance function with mutation will decrease at first and then increase rapidly with the increase of b when ω=4 and ω=9.

The first corollary can be explained on the basis of formula (3.29).Formula (3.29) can be approximated considering the condition 2≫1 as follows

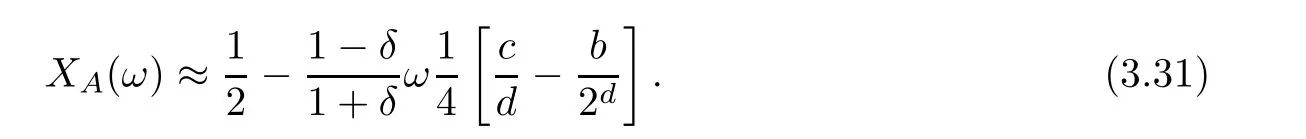
The second corollary can be explained on the basis of the expected payoff function and function h(i,ω).When b <1.5,the average abundance function with mutation will decrease with the increase of b.It can be deduced from Figure 1 that the inequality π(i) >π(i+1)holds in most cases.This means that in the process of the increase of b,the π(i) will become larger than aspiration level α soon,while the π(i+1)is still smaller than aspiration level α at the same time.In other words,π(i)>α and π(i+1)<α.Therefore,more individuals will choose a strategy B under the influence of large selection intensity.Thus the average abundance function will decrease.

When b >1.5,the average abundance function with mutation will increase rapidly with the increase of b and it will get close to 1/2.Also,this trend of approaching 1/2 will increase with the increase of selection intensity ω.The reason for this phenomenon can be explained by the function h(i,ω),defined by formula (3.15).It can be deduced from formula (2.3) that both π(i+1) and π(i) will increase with the increase of b.It can be further deduced that both π(i+1) and π(i) will become larger than aspiration level α when b increases to a very high level (b>1.5).In other words,π(i+1)>α and π(i)>α when b increases to a very high level (b>1.5).The following inequalities will be obtained when considering the fact that selection intensity ω also increases:

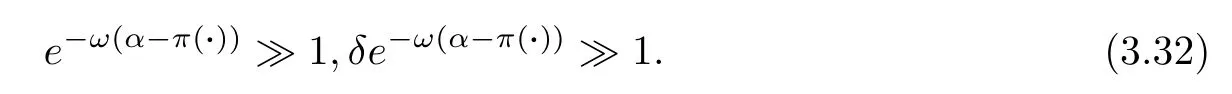
Because of the establishment of formula (3.32),the function h(i,ω) will gradually degenerate to the first part as follows

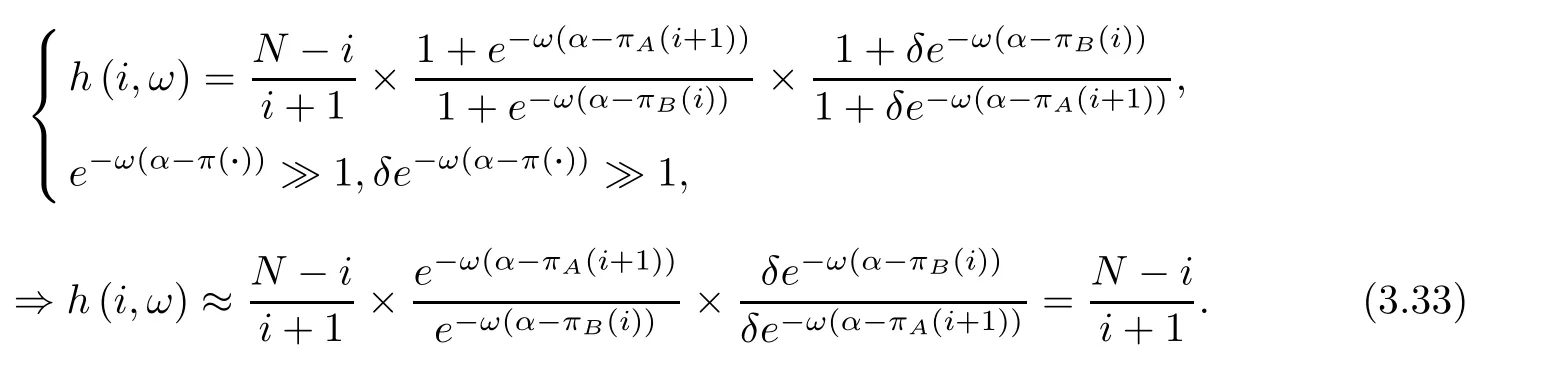
Thus the corresponding average abundance function will gradually get close to 1/2.

3.2.3 The influence of c on the average abundance function with mutation

Figure 6 shows how the average abundance function with mutation changes with cost c.Two corollaries can be obtained from the analysis of Figure 6.

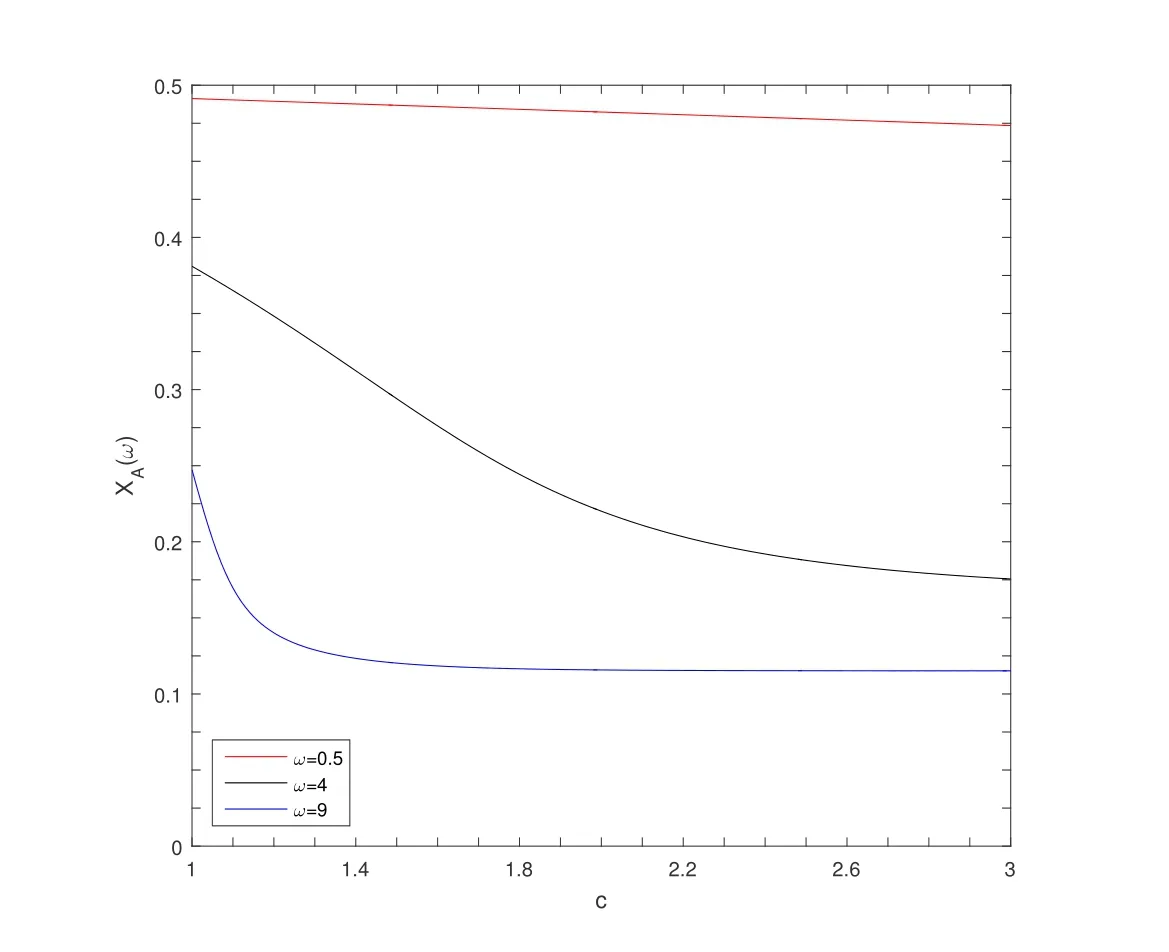
Figure 6 The average abundance function XA(ω) with mutation changes with c in a multi-player snowdrift evolutionary game model (d=15,b=1.5,α=1,N=100,δ=0.03)

Corollary 3.2.3.1

The average abundance function with mutation will decrease slowly with an increase of c when ω=0.5.

Corollary 3.2.3.2

The average abundance function with mutation will decrease at first and then basically remain stable with an increase of c when ω=4 and ω=9.

The first corollary can be explained by formula (3.31) as follows

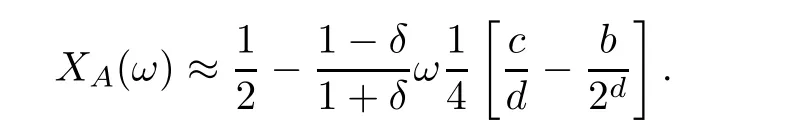
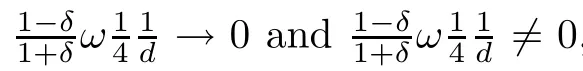
The second corollary can be explained on the basis of formula (3.15).Formula (3.15) can be rewritten as

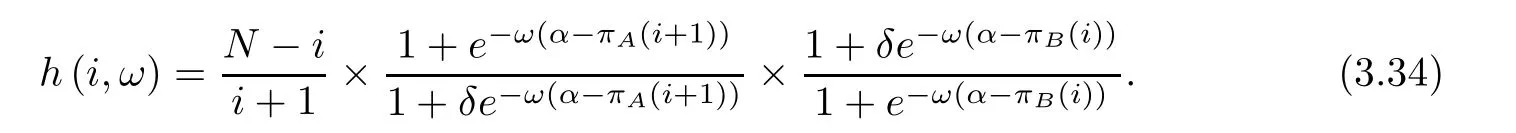
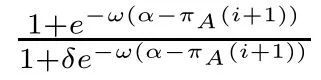
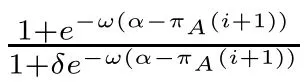
When c keeps increasing (c >1.5),many individuals are required to choose strategy A in order to ensure that π(i+1) >α.On the other hand,a lot of individuals who choose strategy A will turn to choose strategy B because of the effect of mutation.The synthesis of the above two influences will ensure the average abundance function with mutation is basically unchanged when c keeps increasing (c>1.5).

3.2.4 The influence of α on the average abundance function with mutation

Figure 7 describes how the average abundance function with mutation changes with aspiration level α.Two corollaries can be obtained from the analysis of Figure 7.

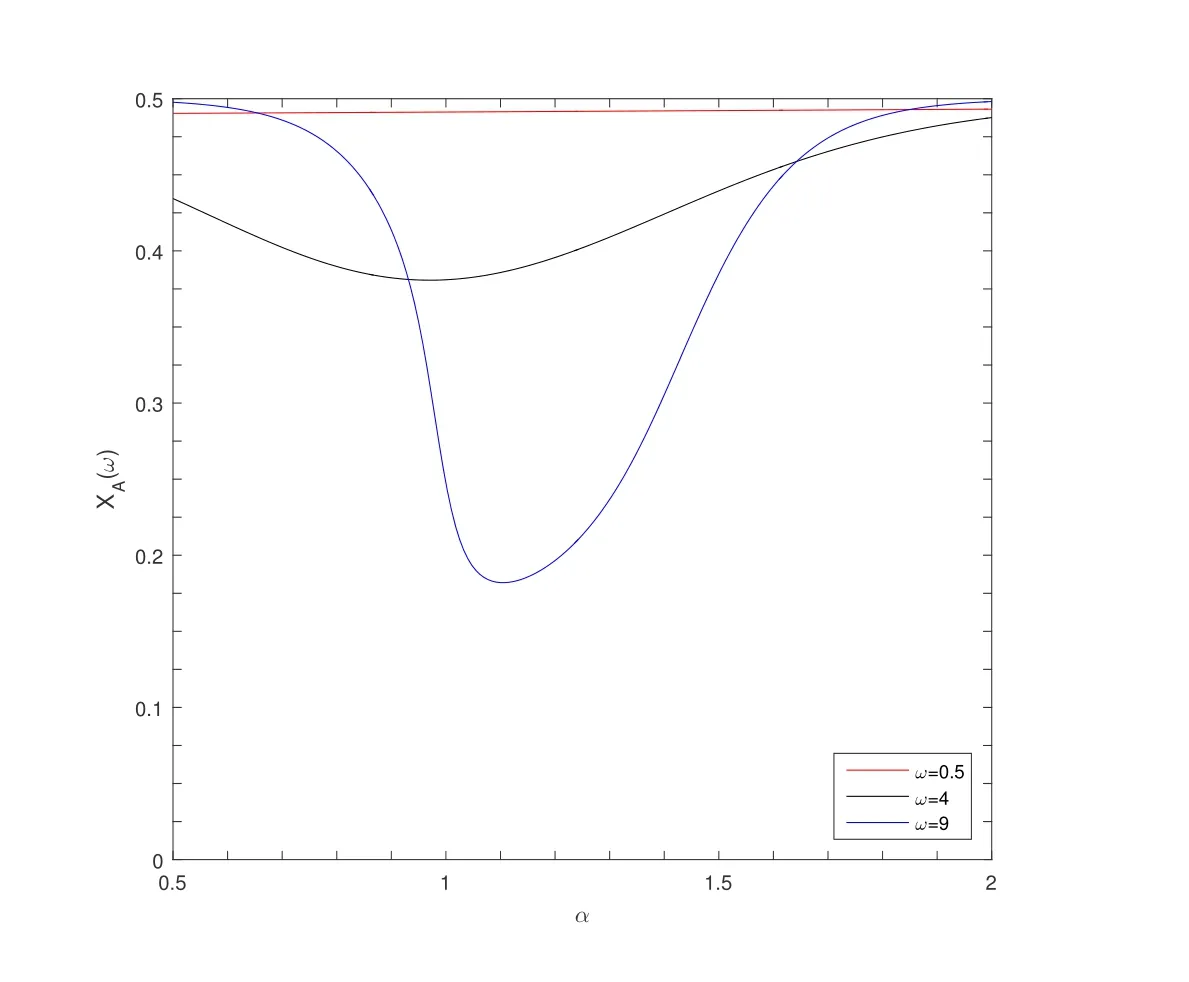
Figure 7 The average abundance function XA(ω) with mutation changes with α in a multi-player snowdrift evolutionary game model (d=15,b=1.5,c=1,N=100,δ=0.03)

Corollary 3.2.4.1

The average abundance function with mutation will basically remain unchanged with the increase of α when ω=0.5.

Corollary 3.2.4.2

The average abundance function with mutation will decrease at first and then increase rapidly with the increase of α when ω=4 and ω=9.

The first corollary can be explained on the basis of formula (3.29):

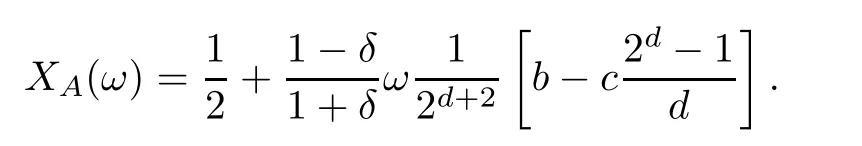
It can be deduced that formula (3.29) is not related to aspiration level α,so the average abundance function is basically independent of the aspiration level α when ω=0.5.

The second corollary can be explained on the basis of the expected payoff function and function h(i,ω).When α<1,the average abundance function will decrease with the increase of α.It can be deduced from Figure 1 that the inequality π(i) >π(i+1) holds in most cases.This means that in the process of the increase of α,π(i+1) will become smaller than aspiration level α soon,while the π(i) is still larger than aspiration level α.In other words,π(i) >α and π(i+1) <α.Therefore,more individuals will choose strategy B under the influence of large selection intensity ω.Thus the average abundance function will decrease.

When α>1,the average abundance function with mutation will increase rapidly with the increase of α and it will get close to 1/2.Also,this trend of approaching 1/2 will increase with the increase of selection intensity ω.The reason for this phenomenon can be explained by the function h(i,ω),defined by formula (3.15).It can be deduced from formula (2.3) that neither π(i+1) nor π(i) is related to aspiration level α.

It can be deduced that both π(i+1) and π(i) will become smaller than aspiration level α when α increases to a very high level (α>1).In other words,π(i+1)<α and π(i)<α when α increases to a very high level (α>1).The following inequality will be obtained when considering the fact that selection intensity ω also increases:

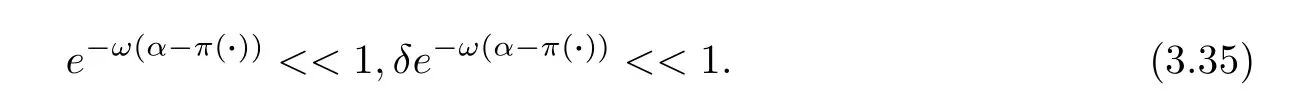
Because of the establishment of formula (3.35),the function h(i,ω) with mutation will gradually degenerate to the first part as follows

Thus the corresponding average abundance function will gradually get close to 1/2.

3.2.5 Inferences

We have studied how the average abundance function X(ω) with mutation changes with parameters from both quantitative and qualitative aspects on the basis of numerical simulation.We obtain the following inferences:

Inference 3.2.1

The effect of parameters d,b,c,α on the average abundance function is slight when selection intensity ω is small.This phenomenon can be explained by the first-order Taylor expansion of the average abundance function with mutation.

Inference 3.2.2

The effect of parameters d,b,c,α on the average abundance function is remarkable when selection intensity ω is large.In particular,the effects of parameters b and α on the average abundance function with mutation are U-shaped to a certain extent.

4 Conclusions and Prospects

4.1 The main research findings of this article

The impact of cooperation and competition[97–105]on social activities[106–114]is becoming very important and this fact is recognized and valued by more and more people with the rapid development of society and of the economy.This promotes the application of evolutionary game theory [115–123]in real society and provides a good social background for us to study evolutionary game theory deeply.

The main research findings of this article are summarized as follows:

1

The concrete expression of expected payoff function on the basis of a multi-player snowdrift evolutionary game model [124,125]has been deduced.The intuitive expression of the average abundance function with mutation has been derived on the basis of the detailed balance condition.These findings pave the way for theoretical analysis and numerical simulation.

2

The first-order Taylor expansion of the average abundance function has been deduced when selection intensity gets close to zero.On this basis,the expression of the average abundance function with mutation can be simplified to a linear function of selection intensity.

3

The approximate expressions of the average abundance function have been deduced in the case of small selection intensity and large selection intensity.The characteristics of the approximate expressions of the average abundance function under different mutation have been analyzed.

4

The effects of various parameters on the average abundance function with mutation have been studied by numerical simulation.The corresponding results have been explained on the basis of the expected payoff function π(·) and function h(i,ω).

4.2 Research Prospects

The research work in this article is a preliminary exploration.Further awareness for research are as follows:

Prospect 1

The influence of a single parameter has been considered when we make numerical simulation on the average abundance function with mutation.The joint influence of multiple parameters is still lacking.On the other hand,the sensitivity analysis of parameters is not enough.This means the above two fields should be taken seriously in the further study.

Prospect 2

We have studied the characteristics of the average abundance function with mutation on the basis of the aspiration rule in a finite,well-mixed population.Corresponding analysis is still lacking for other types of populations or another evolutionary rules.This means that other types of population should be considered and other evolutionary rules should be taken into account.

Prospect 3

It has been found that there is an equivalent substitution relationship between mutation and selection intensity.However,the effects of selection intensity are closely related to the exponential terms as e.This fact makes it difficult to analyze the equivalent substitution relationship mentioned earlier.It is worth thinking about whether the size of mutation can be described by the change of selection intensity in the process of system evolution.

Appendix

Appendix A The proof of formula (3.14)

Appendix B The proof of formula (3.29)