CONTINUOUS DEPENDENCE ON DATA UNDER THE LIPSCHITZ METRIC FOR THE ROTATION-CAMASSA-HOLM EQUATION∗

Xinyu TU(涂馨予)

School of Mathematics and Statistics,Southwest University,Chongqing 400715,China E-mail:xinyutu@cqu.edu.cn

Chunlai MU(穆春来)Shuyan QIU(邱蜀燕)

College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China E-mail:clmu2005@163.com;shuyanqiu0701@126.com

Abstract In this article,we consider the Lipschitz metric of conservative weak solutions for the rotation-Camassa-Holm equation.Based on defining a Finsler-type norm on the tangent space for solutions,we first establish the Lipschitz metric for smooth solutions,then by proving the generic regularity result,we extend this metric to general weak solutions.

Key words coriolis effect;rotation-Camassa-Holm equation;generic regularity;Lipschitz metric

1 Introduction

In the present study,we consider the following rotation-Camassa-Holm(R-CH)equation[20]:

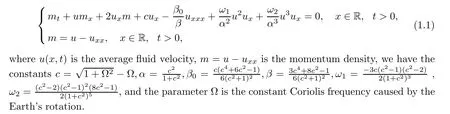
This model equation has nonlocal cubic and even quartic nonlinearities,and a formal Hamiltonian structure.In addition,it has three corresponding conserved quantities as follows:

Note that the rigorous analysis for the systems of pand qwas verified in [24].The solutions consist of a train of infinitely many peaked solitary waves were established in [13],and the existence of a different peaked solution was claimed in [19].As for other related problem,one can refer to [28,29]

Furthermore,the CH equation (1.6) admits bi-Hamiltonian structure in terms of m=u −αu,which can be rewritten as

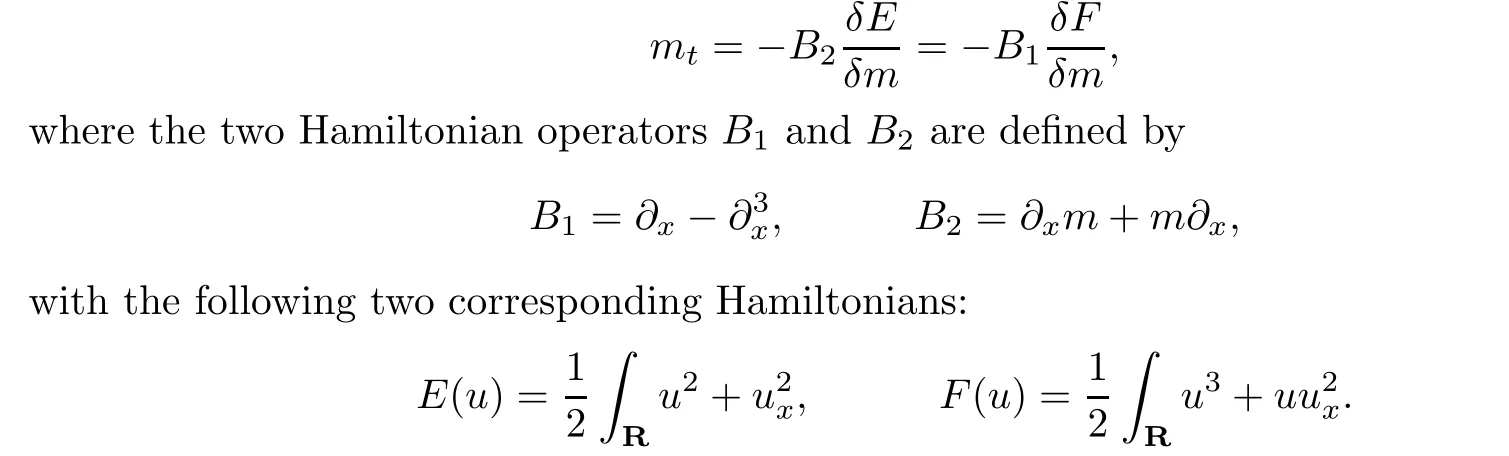
So far,many works have been written on the CH equation.Here we are mainly concerned with issues pertaining to the weak solutions.The solution to the Camassa-Holm equation can be continued after wave-breaking as either a global conservative or a global dissipative weak solution,as was shown in [5,6].The uniqueness for the conservative solution or dissipative solution of the CH equation was shown in [4,26].Furthermore,the Lipschitz metric for the CH equation was established in [9].

Notice that all nonlinear terms in the CH equation are quadratic,which inspires study of those integrable equations with higher-power nonlinear terms.In [30],for the R-CH equation,which exhibits a cubic and even quartic nonlinearities,in light of the standard ODE theory and the energy estimates,we obtained the existence and uniqueness of the global conservative weak solution in the Sobolev space H(R).

Here,the optimal transport metric can be determined by the minimum cost to transport an energy measure from one solution to the other.

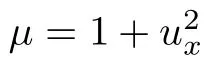
Inspired by the idea in[25],depending on an application of Thom’s Transversality Theorem,we have the following generic regularity result:

We now state the main theorem of this paper.

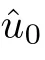
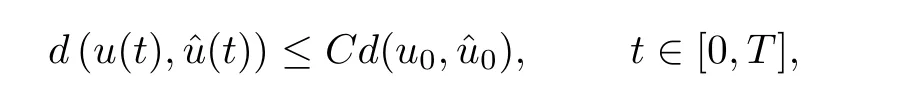
where the constant C depends only on T and the H(R) norm of initial data.

The rest of this article is organized as follows:in the next section,we recall some conservation laws and useful inequalities regarding the rotation-Camassa-Holm equation obtained in[30].In Section 3,we establish the Lipschitz metric for smooth solutions to the R-CH equation.Section 4 is devoted to the generic regularities of conservative weak solutions to the R-CH equation.Finally,in Section 5,we first extend the result obtained in Section 3 to piecewise smooth solutions with only generic singularities,and then to general weak solutions.

2 Preliminary

In [30],we already established the global existence and uniqueness results of the weak solution for the R-CH equation.Our goal in this section is to recall some conservation laws and useful inequalities obtained in [30].

First,we write the initial problem for the R-CH equation in the weak form

where the source term P is defined as (1.5).

Differentiating the first equation in (2.1) with respect to the variable x,we obtain

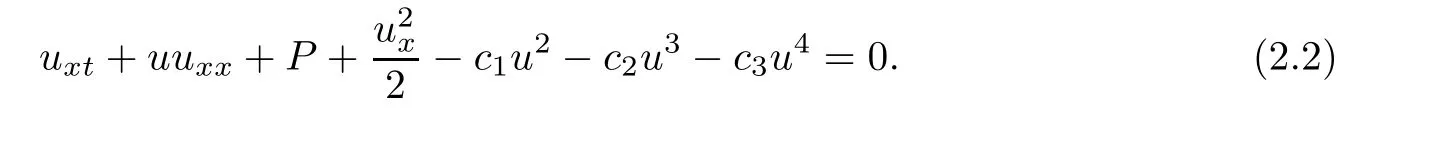
3 Finsler Norm on Tangent Vector When Solutions Are Smooth

To construct the Lipschitz metric,our attention in this section is turned to establishing the Finsler norm on tangent vectors when solutions to (2.1) are smooth.Moreover,we show how this norm changes in time.To see this,we consider a smooth solution u to (2.1),and we take a family of perturbed solutions u(x) to (2.1) of the form

Here,v measures the vertical displacement between two solutions.A direct computation such that the first order perturbation v satisfies

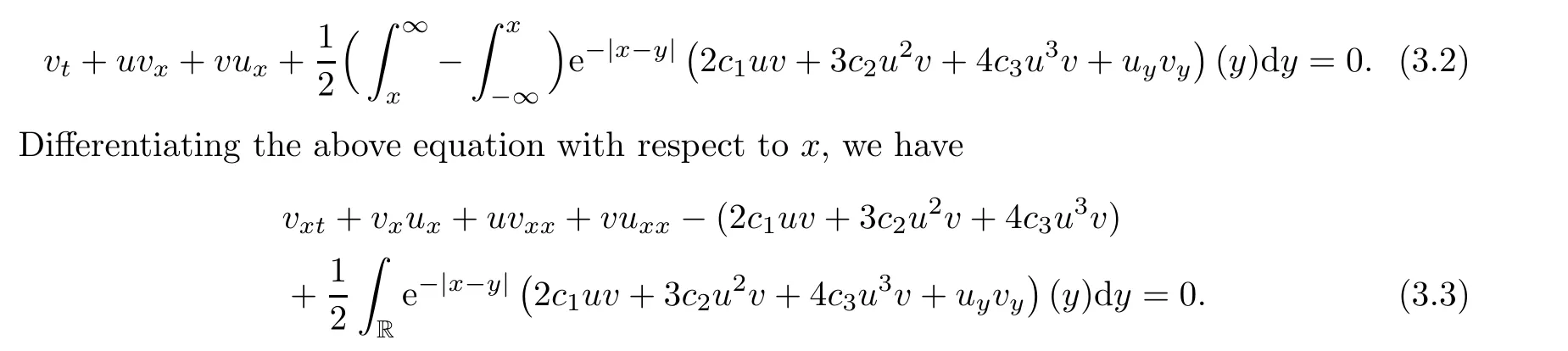
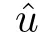
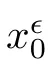
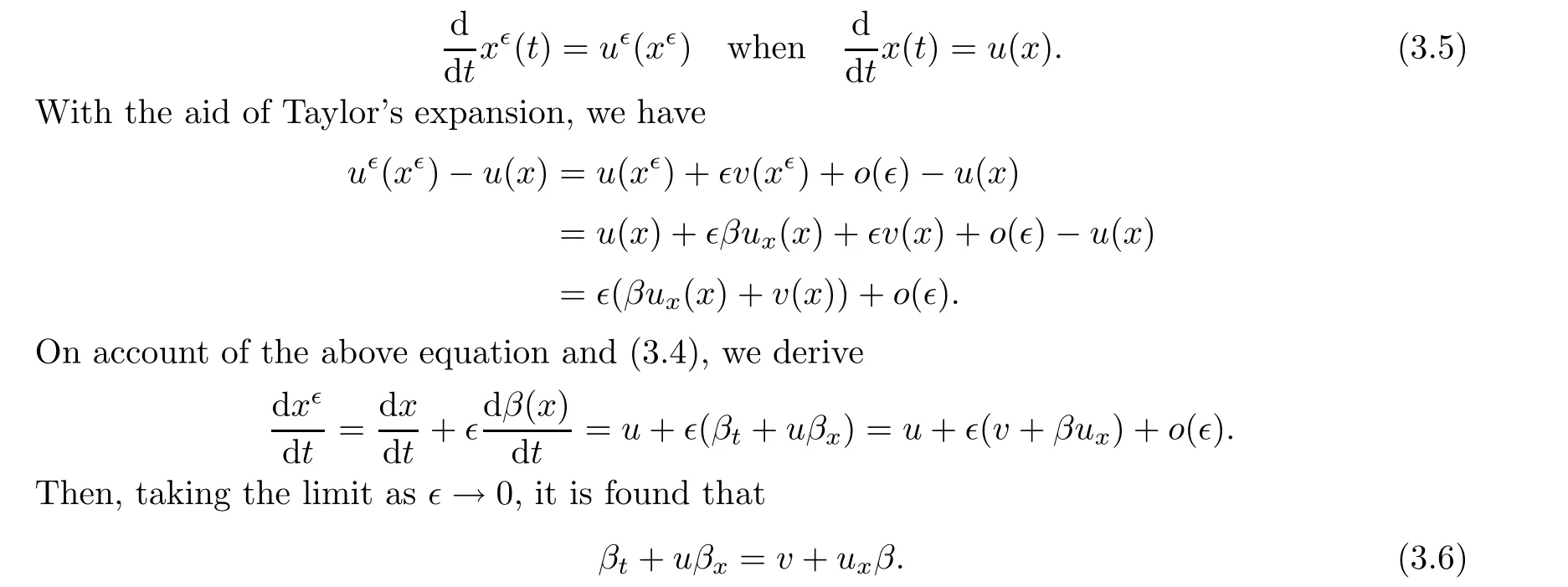
Notice that u is always smooth in this section,therefore,for given smooth initial data β(0,x)=β(0),it is easy to obtain the solution β of (3.6).Hence,we can define the admissible set as

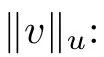
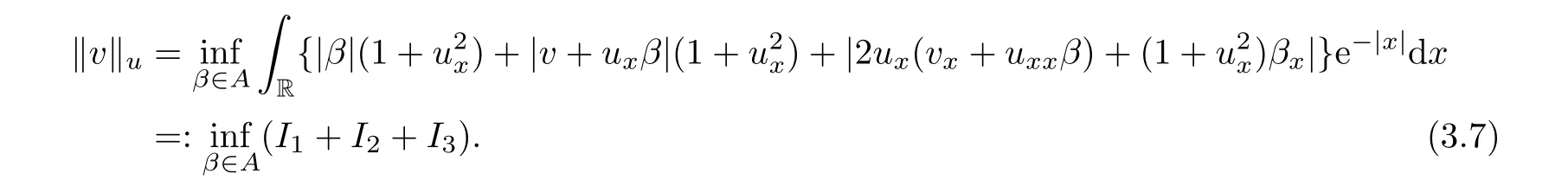
Now,we enter into a set of calculations to show how the norm (3.7) changes in time.

Lemma 3.1

For any T >0 fixed,let u(t,x) be a smooth solution of (2.1) for t ∈[0,T].Suppose that v and β satisfy equations (3.2),(3.3) and (3.6).Then the inequality

holds for all t ∈[0,T],where C(T) is a constant depending only on T and initial energy E(0).

Proof

Note that (3.8) can be achieved by proving that

where C is a constant depending only on E(0).Therefore,we will concentrate on proving(3.9).Here and below,we make use of the notation C to represent the constant which depends upon E(0).

4 Generic Regularity of Solutions to the R-CH Equation

In this section,first,relying on the construction of several families of perturbations for a given solution of the semi-linear system introduced in [30],we prove the generic regularity of conservative solutions to the R-CH equation given in Theorem 1.1.Next,some propositions,definitions and corollary are given.

4.1 Generic regularity to solutions of Theorem 1.1

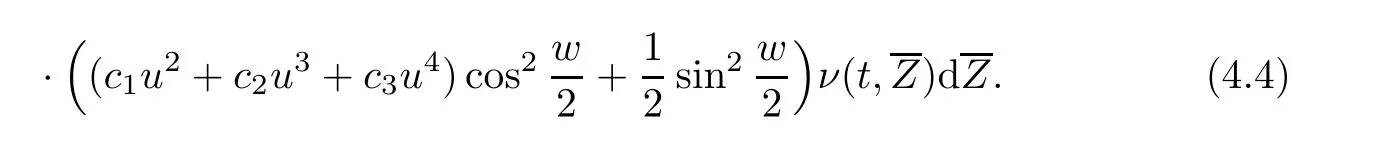
In [30],we already proved the global existence and uniqueness of the energy conservative weak solutions in H(R) to (2.1).In addition,we have that the following result also holds:

Lemma 4.1

Suppose that(x,u,w,ν)(t,Z)is the solution of (4.1)–(4.2)with ν >0.Then the set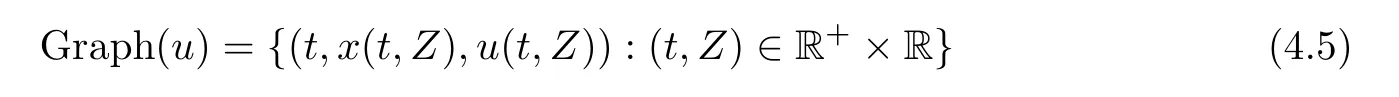

is the graph of a unique conservative solution to the R-CH equation (2.1).

Next,our attention is turned to constructing several families of perturbed solutions to(4.1).To this end,we give the following lemma (for the proof of lemma 4.2,one can refer to [25]):

Lemma 4.2

Let u(t) :R →R,f be a Lipschitz continuous function.For any ODE system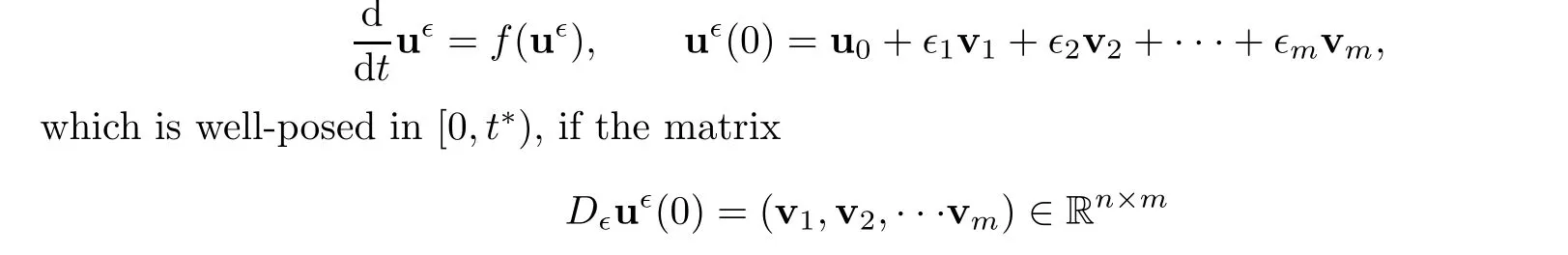

satisfies rank(Du(0))=k,then rank(Du(t))=k for all t ∈[0,t].

Lemma 4.3

Fix any point (t,Z) ∈R×R,and let (u,w,ν) be a smooth solution of(4.1).Suppose that (w,w,w)(t,Z)=(π,0,0).Then there exists a 3-parameter family of smooth solutions (u,w,ν) of (4.1),depending smoothly on ϑ ∈R,which satisfies that

(i) when ϑ=0 ∈R,one recovers the original solution,that is,(u,w,ν)=(u,w,ν);

(ii) at the point (t,Z),when ϑ=0,one has

Proof

Let (u,w,ν) be a smooth solution to (4.1),and fix the point (t,Z).Differentiating the second equation in (4.1) with respect to Z,one obtains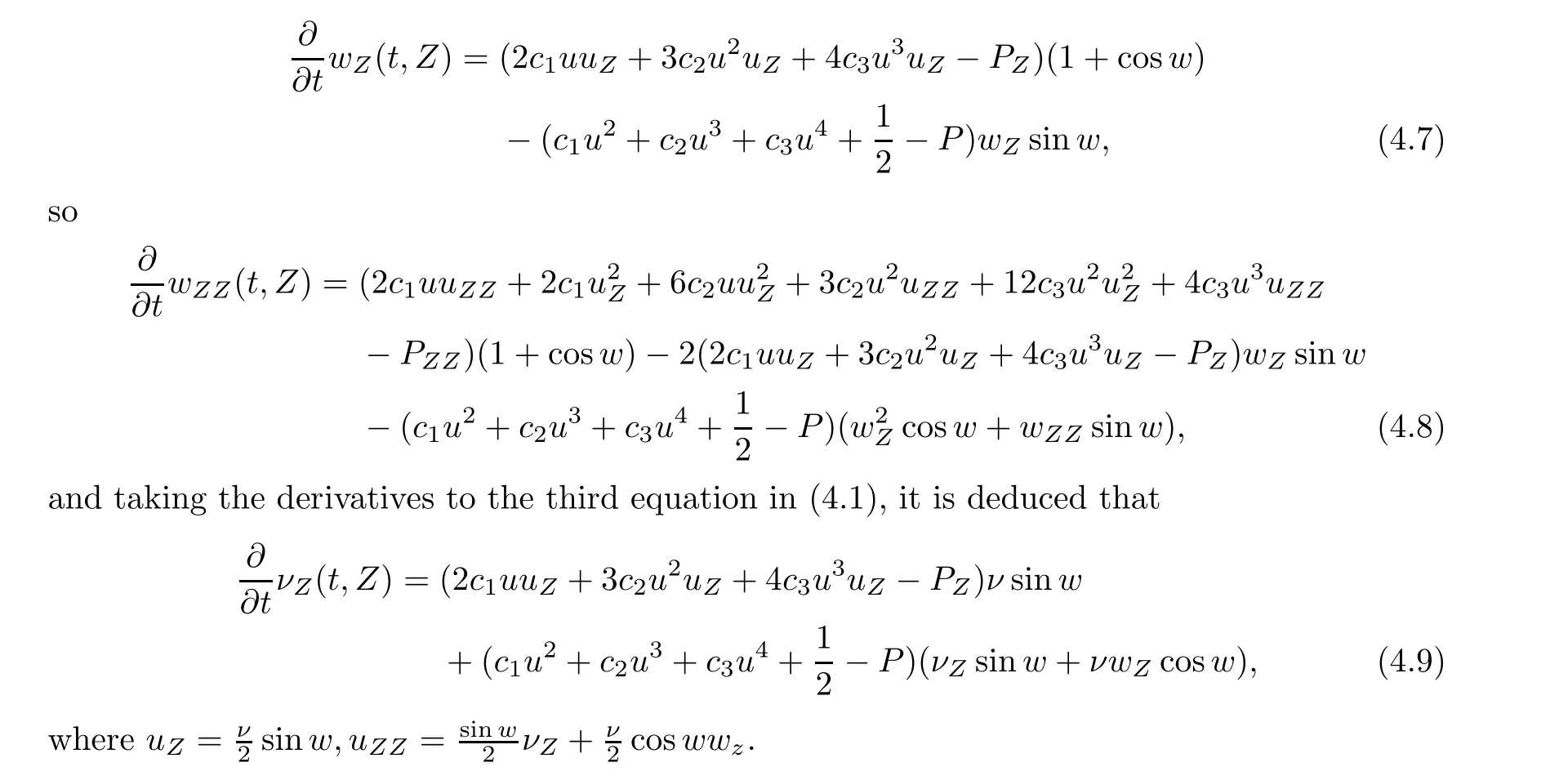

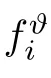
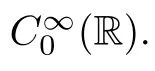
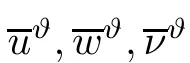
The following lemma can be achieved by Lemma 4.3 and the Transversality argument[1,23,25],which gives the generic structure of {(t,Z);w(t,Z)=π}:

Lemma 4.4

For any compact domain Ω:={(t,Z);0 ≤t ≤T,|Z|≤M},let S be the set of all Csolutions (u,w,ν) to (4.1),with ν >0 for all (t,Z) ∈R×R.In addition,denote S⊂S as solutions (u,w,ν) with the property that for (t,Z)∈Ω,neither the value

The preceding lemmas lead to a proof of the generic regularity result for the conservative solutions.

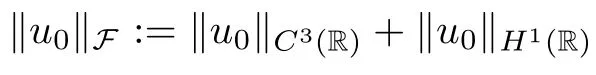
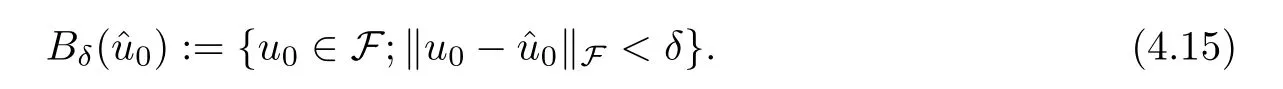
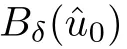
Step 1

Our attention is now turned to constructing D.It follows from the definition of F that for u∈F,we have

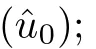
(ii) For any (t,Z) ∈{(t,Z);(t,x(t,Z)) ∈ℵ},the solution (u,w,ν) of (4.1) never satisfies(4.14).

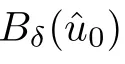
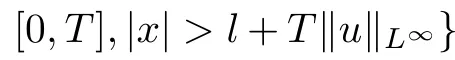
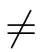
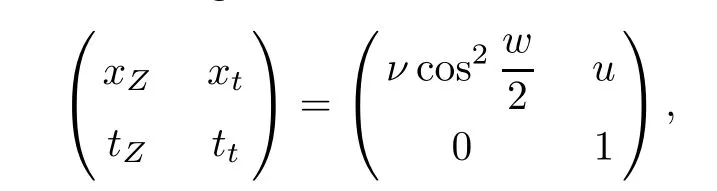
due to the fact that the uniform positivity and boundedness of ν hold on compact subsets,and so in some neighborhood of (t,x(t,Z)),the coordinate change (t,Z) →(t,x) is locally invertible.Thus,the solution u is C.

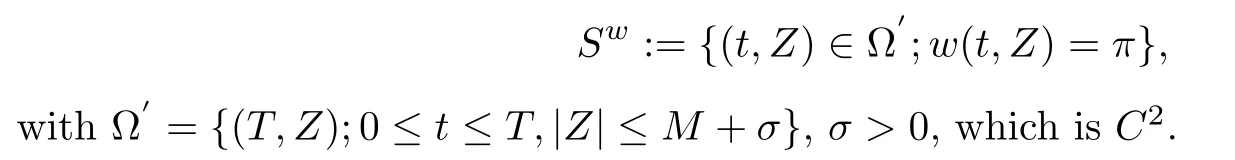
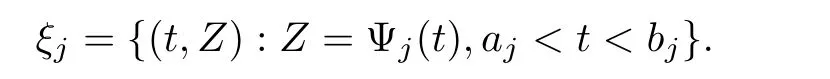
4.2 Solution Paths

5 Metric for General Weak Solutions

Inspired by [9],we first extend the Lipschitz metric to piecewise smooth solutions.Then we use the generic regularity result to extend the Lipschitz metric for general weak solutions.

5.1 Length of piecewise regular paths

Let u(t,x) be a reference solution to (2.1),and let u(t,x) be a cluster of perturbations.In the t −Z space,we define (x,u,w,ν) to be the smooth solution of (4.1)–(4.2),and set the perturbation

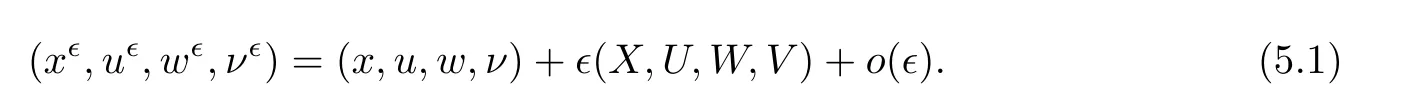
The smoothness of the coefficients in (4.1)–(4.2) guarantees that the first order perturbations are well defined for (t,Z) ∈R×R,which also satisfies a linearized system.Then,by simple computation,we obtain the following equalities which express the terms in (3.7) are in accordance with (X,U,W,V):

Applying Lemma 3.1,we can further obtain the following Lipschitz property (for brevity,we skip the proof;the readers can refer to [9]):

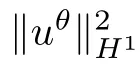
5.2 Construction of the geodesic distance for general weak solutions

Now,we aim to construct a geodesic distance,under which the general weak solution generated by the R-CH equation is Lipschitz continuous.

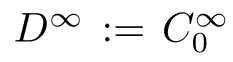
First,for a constant E>0,we write

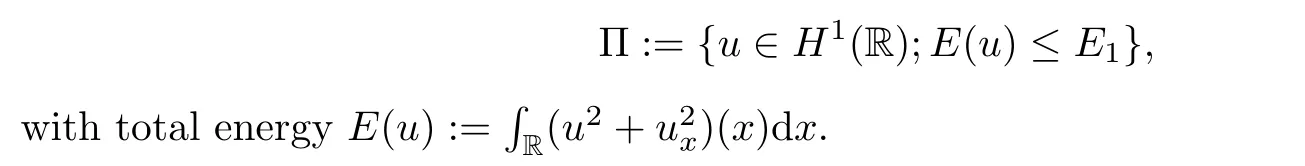
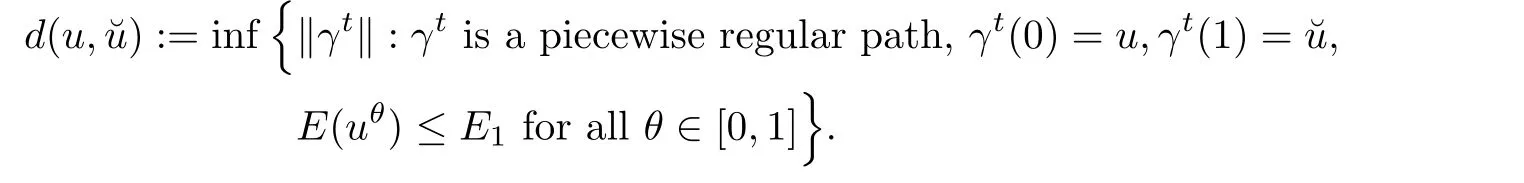
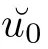
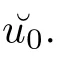
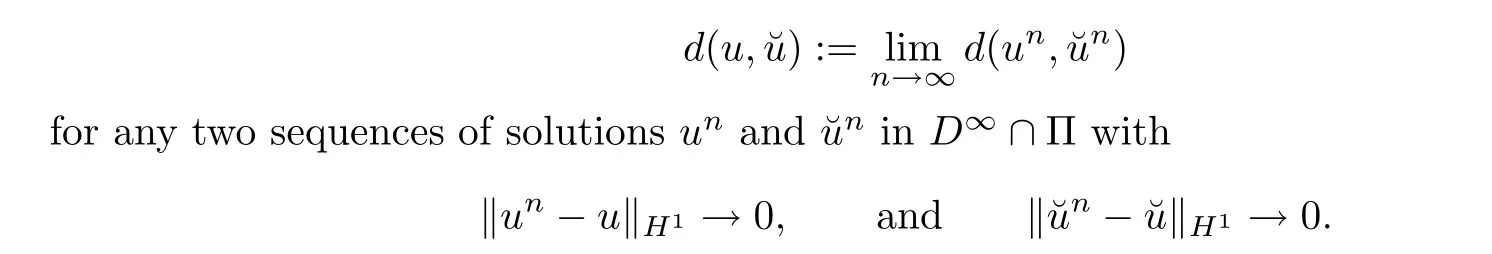
On account of the Lipschitz property of the solution flow in D∩Π,the path remains piecewise regular after concatenation and a suitable re-parameterization,which implies that the definition of the metric d is well-defined.