A GENERALIZED RESULT ON THE POLYNOMIAL-LIKE ITERATIVE EQUATION∗
2021-04-08PingpingZHANG张萍萍
Pingping ZHANG(张萍萍)
College of Science,Binzhou University,Binzhou 256603,China E-mail:ppz.2005@163.com
Yingying ZENG(曾莹莹)†
School of Mathematical Sciences and V.C.&V.R.Key Lab of Sichuan Province,Sichuan Normal University,Chengdu 610068,China E-mail:mathyyz@163.com
Abstract Most results on the polynomial-like iterative equation are given under the condition that the given function is monotone,while a work by L.Liu and X.Gong gets nonmonotone PM solutions with height 1 when the given function is of the same case.Removing the condition on height for the given function,we first give a method to assert the nonexistence of C0solutions,then present equivalent conditions for the existence of PM solutions withfinite height.Finally,as an application of the equivalent conditions,we construct the PM solutions in the case that the given function has one fort.
Key words height;characteristic interval;fort;PM function
1 Introduction

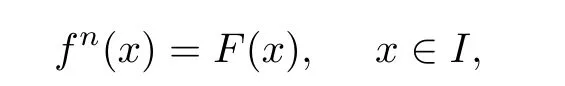
where F:I→I is a given self-map.
In recent years,as a generalization of iterative roots,the polynomial-like iterative equation

has attracted a lot of attention([3,5,7,8,14]).Here λs(i=1,2,···,n−1)are real constants and the known function F may not be a self-map.
For strictly monotone function F,different kinds of solutions of eq.(1.1),such as continuous([9,19]),smooth ([4]),analytic ([12]),convex ([6]) and equivariant ([17,18]) solutions,have been investigated widely.For non-monotone function F,the results (e.g.periodic solution([11])) are relatively few.Recently,for a given PM function F with height H(F)=1,the PM solutions f of eq.(1.1) are investigated in [10].
In this paper,we address the following question:without the assumption that H(F)=1,do there exist PM solutions f of eq.(1.1) for the general PM function F :I →F(I)? We first give sufficient conditions on the nonexistence of Csolutions of eq.(1.1),then present sufficient and necessary conditions on the existence of PM solutions f,and illustrate though examples that the existence of solutions is independent of the relation between S(F) and S(f).Finally,as an application of the equivalent conditions,we construct PM solutions in the case that the given function has one fort.
2 Nonexistence of C0 Solutions
In this section we present a method to assert the nonexistence of all Csolutions of eq.(1.1).Let Λ:=1+λ+λ···+λ.Then we have
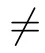
Proof
By reductio ad absurdum,suppose that eq.(1.1) has a Csolution f :I →I.We say that f has at least one fixed point x∈I since f is a self-map on I.Note that
We present two examples to illustrate Theorem 2.1.
Example 2.2
Consider the equation
The point s:=1/2 is the unique fort of F.By simple calculation,we get that Λ=0 and that there is no ξ∈[0,1]such that F(ξ)=0.By using (i) of Theorem 2.1,there exists no Csolution f :I →I of eq.(2.1).

Note that s:=1/4 is the unique fort of F and that Λ=1/2.Since there is no ξ∈I satisfying Λξ=F(ξ),then,according to (ii) of Theorem 2.1,there exists no Csolution f :I →I of eq.(2.2).
3 Existence of PM Solutions
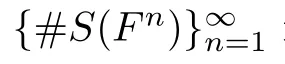
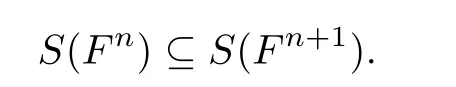
Let the least nonnegative integer k such that S(F)=S(F) be the height H(F) of F.Otherwise,the height satisfies that H(F)=∞.
Denote the interior of I by intI.For a PM function f :I →I with H(f)∈(0,∞),we list all t∈S(f)⊆intI (i=1,2,···,N),such as

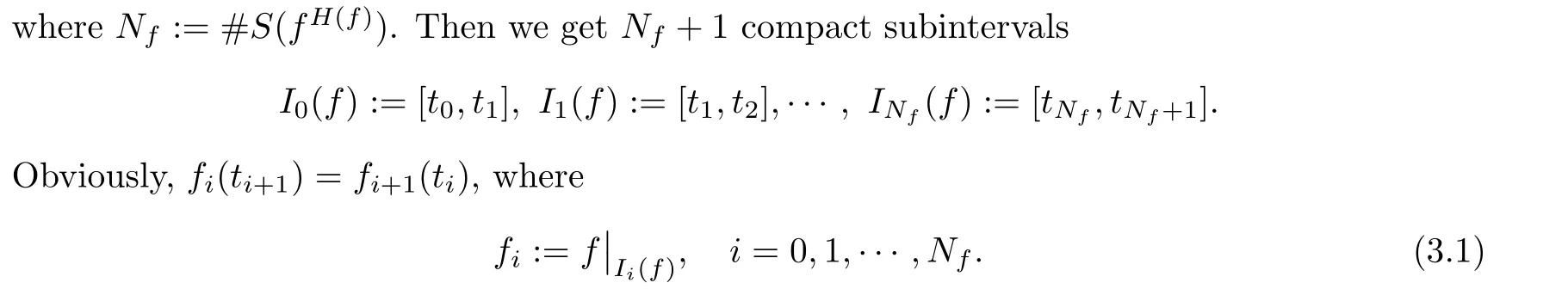
The following Lemma is used in the paper:
Lemma 3.1
(see [15,Theorem 2.2]) Let f :I →I be a PM function with a unique fort xand let
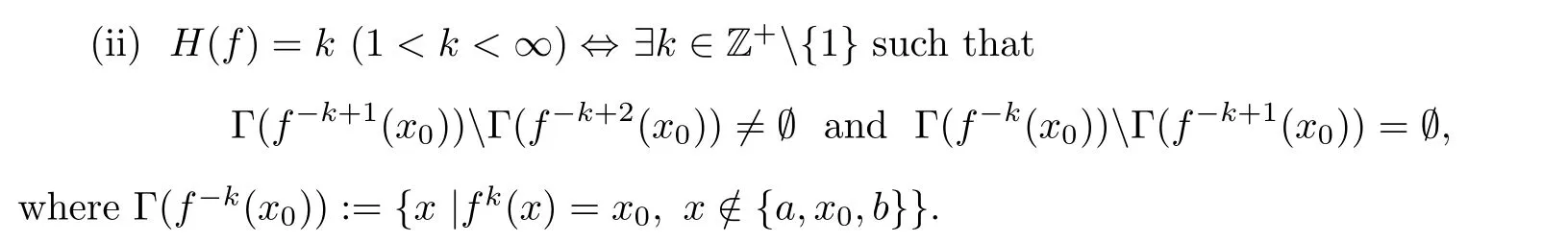
In this section we give equivalent conditions for the existence of PM solutions of eq.(1.1).Moreover,we illustrate that the existence of said solutions is independent of the relation between S(F) and S(f) by an example.
For given functions gand g,denote g:=g◦gif g◦gis well defined.We present now our main results.
Theorem 3.2
For a given PM function F :I →F(I),a function f :I →I with H(f)∈(0,∞) is a solution of eq.(1.1) if and only if fsatisfies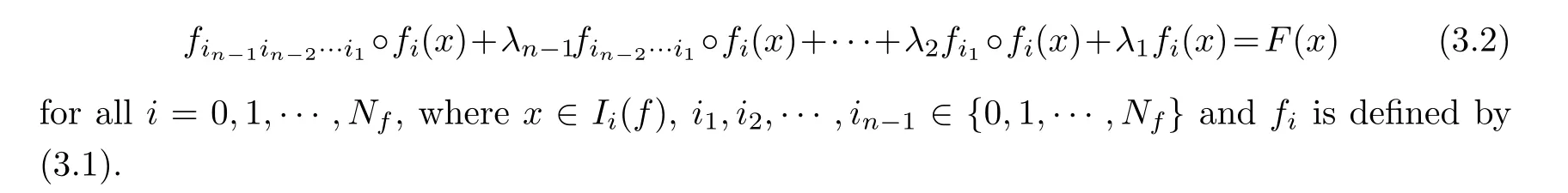
Proof
Necessity.Note that f is a solution of eq.(1.1) and H(f)∈(0,∞).We first show that fmaps I(f) into a subinterval I(f) for some i∈{0,1,···,N}.
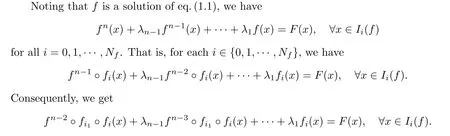
Repeating the same procedure as above,we eventually get the formula (3.2).

Remark 3.3
Without the assumptions that H(F)=H(f)=1,Theorem 3.2 is a generalization of Theorem 3.1 in [10].Remark 3.4
Let f be a PM solution of eq.(1.1) with a given PM function F.Even if S(f)⊆S(F) ([10,Lemma 2.1]),the sets S(f) and S(F) are independent.Now we give an example to illustrate Theorem 3.2.
Example 3.5
Consider the equation

4 Construction of PM Solutions
As an application of Theorem 3.2,in this section we construct the PM solution f of a class of eq.(1.1).Assume that
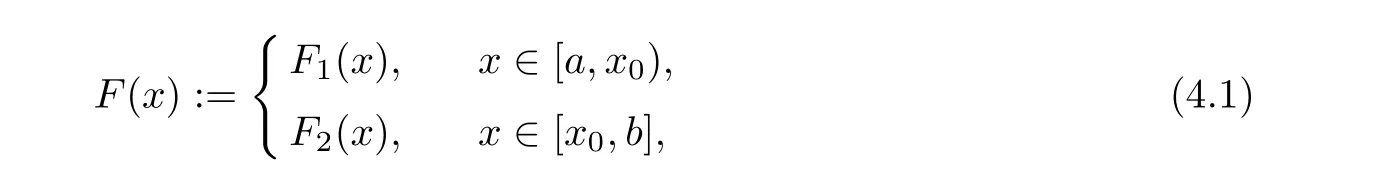
where F,Fare Cfunctions and Fis strictly increasing and Fis strictly decreasing.The other case (Fis strictly decreasing and Fis strictly increasing) can be changed into the first case by G(x):=b −a −F(x).Note that F has three cases:
(i) F(x)≤x,
(ii) F(x)>xand F(b)≥x,
(iii) F(x)>xand F(b) We define the subinterval Iof interval I as Theorem 4.1 Proof Case (i) In fact,by the assumption,we have There are two subcases N In this manner we get all f(i=1,2,···,N),one after another,and that can be presented as f,f,f,···,f.Linking all f,f,···,fup as f,fand fform a PM solution f of eq.(1.1). For the subcase N≥n,we can construct f(i=1,2,···,n−1)by using f,f,f,···,fas that of the subcase N This contradicts the fact that F has finite height,according to Lemma 3.1,which implies(4.8).Consequently,by using Lemma 3.1,we say that In what follows we give an example to illustrate Theorem 4.1. Example 4.2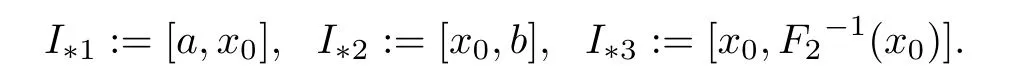

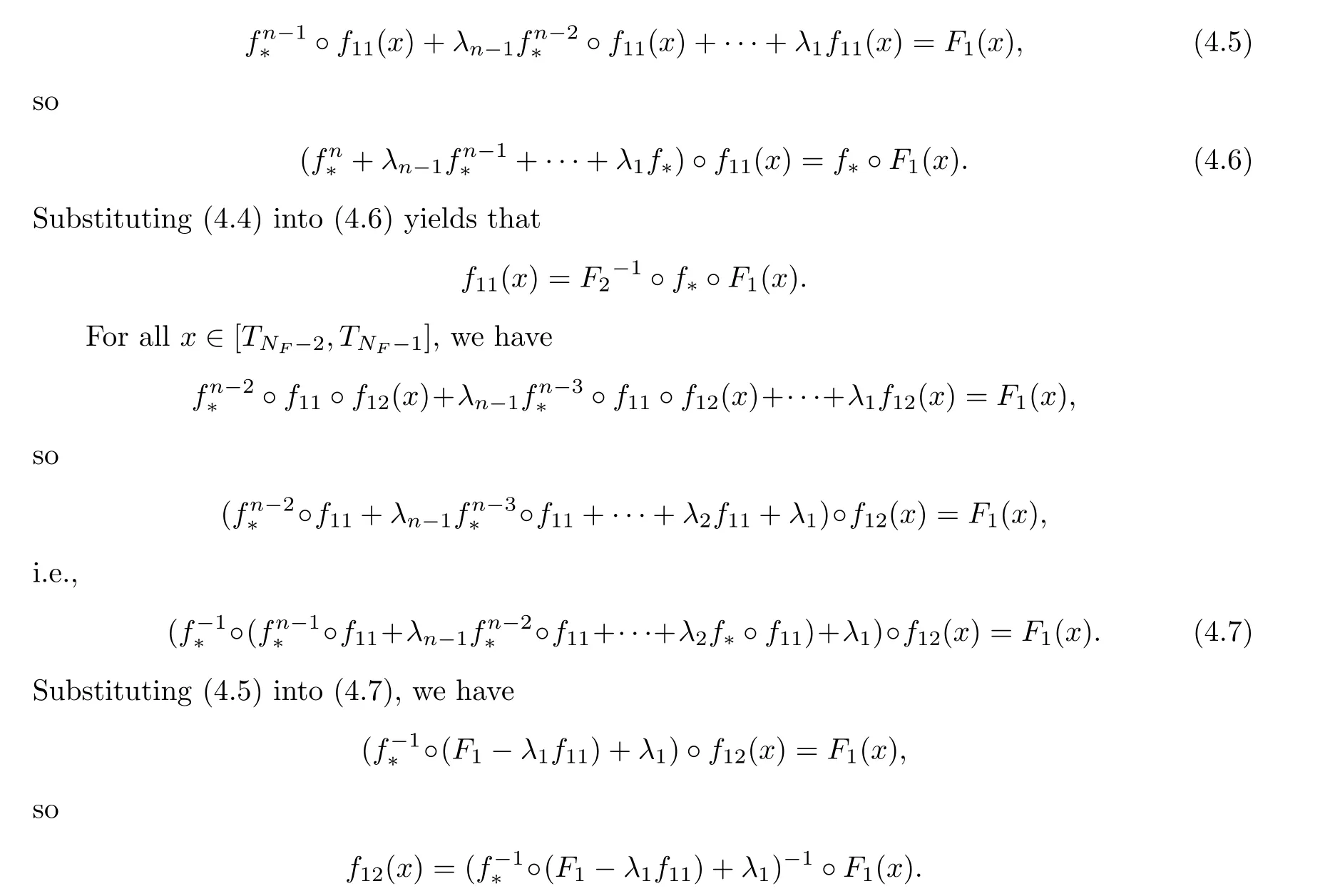


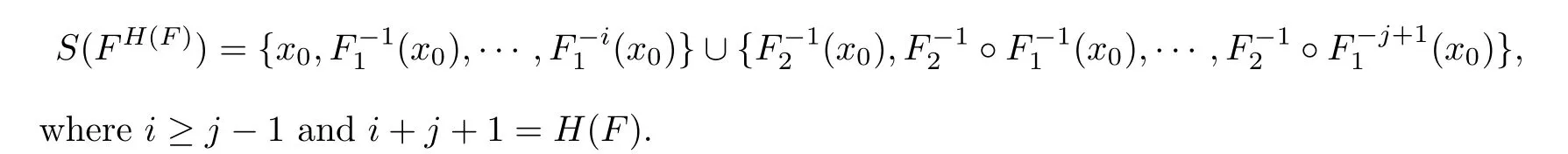
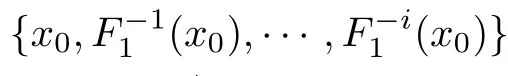
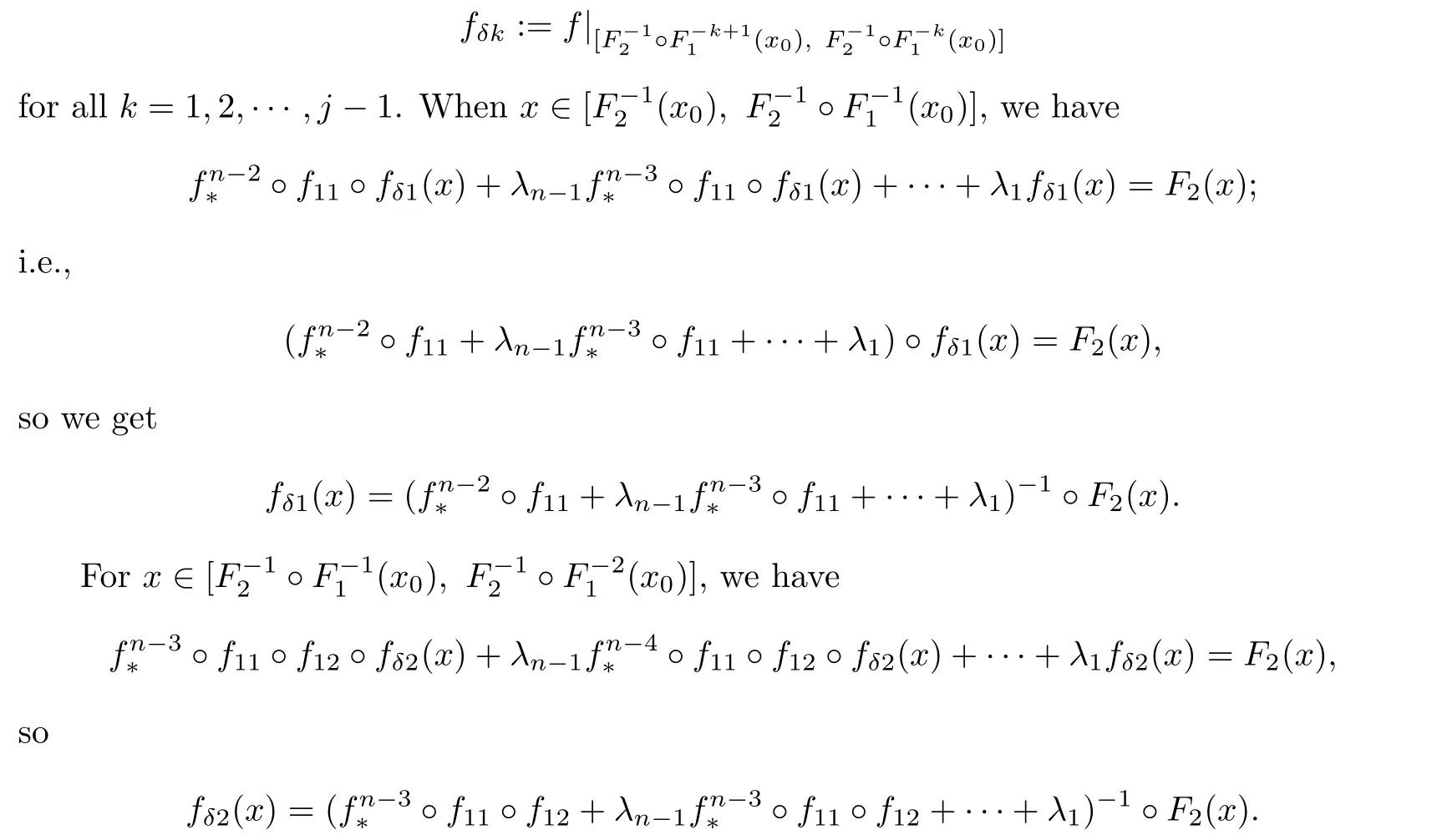



杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- CONTINUOUS DEPENDENCE ON DATA UNDER THE LIPSCHITZ METRIC FOR THE ROTATION-CAMASSA-HOLM EQUATION∗
- WEAK SOLUTION TO THE INCOMPRESSIBLE VISCOUS FLUID AND A THERMOELASTIC PLATE INTERACTION PROBLEM IN 3D∗
- ISOMORPHISMS OF VARIABLE HARDY SPACES ASSOCIATED WITH SCHRÖDINGER OPERATORS∗
- HITTING PROBABILITIES OF WEIGHTED POISSON PROCESSES WITH DIFFERENT INTENSITIES AND THEIR SUBORDINATIONS∗
- INHERITANCE OF DIVISIBILITY FORMS A LARGE SUBALGEBRA∗
- SOME SPECIAL SELF-SIMILAR SOLUTIONS FOR A MODEL OF INVISCID LIQUID-GAS TWO-PHASE FLOW∗
