基于无味变换的边坡可靠性分析
2021-04-07向子林许晓亮黄闻捷陈将宏
向子林 许晓亮 黄闻捷 陈将宏


摘 要:岩土工程不确定性问题是近年研究的热点之一,以边坡可靠性分析为出发点,通过介绍无味变换原理,给出基于无味变换的边坡可靠性分析方法及实施步骤,借助已有研究中的均质边坡和分层边坡算例,探讨了基于无味变换的边坡可靠性分析方法的合理性和适用性,结果表明:基于无味变换原理开展边坡可靠性分析可不依赖于变量的分布类型,应用方便且计算效率高;在分析可靠性较高的边坡时,由于失效概率量值较小,引起的相对误差较大,应谨慎选择,但对于工程上更为关注的可靠性较低(较高失效概率,Pf>7%)的边坡,与蒙特卡洛方法相比,基于无味变换方法的计算结果相对误差约在5%以内,且变量相关系数的变化引起的误差波动较小,适用性较好。
关键词:边坡;可靠性分析;无味变换;抗剪强度参数;相关性;失效概率
中图分类号:TU457 文献标志码:A 文章编号:2096-6717(2021)02-0076-08
Abstract: The uncertainty problem of geotechnical engineering is one of the research hotspots in recent years. The slope reliability analysis is a foundation.According to the principle of unscented transformation,the analysis methods and implementation steps of slope reliability are given.Based on the existing examples of the homogeneous slope and the layered slope, the rationality and applicability of slope reliability analysis method based on unscented transformation are discussed. The results show that the reliability analysis of slope based on the unscented transformation does not depend on the distribution types of variables,and this method is convenient in application and efficient in calculation. When the slope with higher reliabilityis analyzed,a large relative error is caused because the value of failure probability is small.Therefore, the method should be chosen carefully.But for the slope with lower reliability (higher failure probability,Pf>7%) is more concerned in the engineering,the method of slope reliability analysis has better applicability than the Monte Carlo method. Mean while,the relative error of this method is approximately within 5% and the error fluctuation caused by the change of variable correlation coefficient is small.
Keywords:slope; reliability analysis; unscented transformation; shear strength parameters; correlation; failure probability
由于边坡工程岩土体力学参数及破坏模式的随机性和复杂性,可靠性分析逐渐成为了边坡稳定评价及工程设计的另一主要途径和参考依据[1-2]。
目前,在边坡可靠性分析方面的研究大致可以分为两类[3]。一类是边坡单一破坏模式的单元可靠性分析,如:祝玉学等[4]研究了岩质边坡双滑面破壞模式的可靠性计算方法;Low[5]提出了基于Excel的可靠指标计算新算法,并将结果用于岩质边坡单滑面破坏的可靠度分析,采用Beta分布描述黏聚力和摩擦角的分布,采用截尾指数分布描述张裂缝中充水深度系数的分布。第二类是多滑面或多个失效模式的边坡体系可靠性分析,如郑智洋等[6]利用双折减系数法对多滑面边坡稳定性进行分析和研究;谭晓慧等[7]采用Ditle-vsen窄界限公式估算了岩质边坡各失稳模式组成的串联体系的可靠指标;Jimenez-Rodriguez等[8]提出了采用不相交的割集来分析楔体多失效模式的体系可靠度问题,并采用顺序条件重要抽样方法计算体系可靠指标。
与此同时,在传统的一阶可靠度分析方法(first-order reliability,FORM)、蒙特卡洛法(Monte Carlo method,MCS method)、响应面法(response surface methodology,RSM)的基础上,新的边坡可靠性分析方法也不断得到了丰富和发展,如随机有限元法[9]、重要抽样法[10]、copula积分法[2,11],分别在变量相关性描述、高效抽样、功能函数逼近方面做了有益的探索。上述方法中,蒙特卡洛法作为计算失效概率最直接的方法,其计算精度高,已被广泛应用,但当需要大量抽样时,蒙特卡洛法的计算效率较低,特别是对于复杂系统的多维相关变量及非线性问题的求解;此外,工程中比较常用的中心点、验算点等一阶可靠度分析方法通常需要将相关非正态变量进行独立化和标准化[12],增加了计算的近似程度与复杂程度。
因此,有必要进一步探究具有更大灵活性、更高计算效率和更强非线性处理能力的边坡可靠性分析方法。无味变换[13-16]是利用变量的均值和协方差来近似其非线性转换后变量统计特性的方法,相对于蒙特卡洛及一阶可靠度分析方法等,具有计算效率高、精度高(均值、协方差传播精度均可达到二阶以上)、不依赖于分布类型以及应用方便(无需求解非线性方程的Jacobi矩阵[14],甚至无需知道非线性方程的显式方程)等优点,能够较好地处理高维抽样及非线性传递问题,已在自动控制、导航制导、人工智能等领域得到成功的应用[13]。笔者将无味变换引入到边坡可靠性分析之中,给出了基于无味变换的边坡可靠性分析方法,开展了算例边坡的可靠度指标和失效概率计算,并通过不同方法结果的对比分析,阐述所提出方法的合理性和适用性。
1 基于无味变换的边坡可靠性分析方法
1.1 无味变换原理介绍
传统线性化方法的基本思路是对非线性映射做某种线性近似,然后再运用各种线性近似的方法进行分析,相比较于传统的线性化方法,用有限的参数来近似随机变量的概率特性要比近似任意的非线性映射函数更为容易,而且用更少的计算量可以达到更高的精度。基于此,Savin等[15]、Julier等[16]提出了无味变换(unscented transformation,UT),其核心在于借助有限个特征点的信息来近似表达n维随机变量的整体信息(概率密度函数)。
假设有随机变量x的均值矩阵为mx,协方差矩阵为Vx,随机变量y是关于x的函数,通过式(1)所示方式进行映射。
1.2 基于无味变换的边坡可靠性分析步骤
无味变换计算效率高,运用方便[13],能够用有限的数据点信息近似整体概率分布信息,且不依赖于变量的分布类型,可用于边坡工程的可靠性分析。此时,通过确定抗剪强度参数黏聚力c和摩擦角φ等随机变量的均值、方差,并借助FS=f(c,φ,…)映射关系(即功能函数),便可得出安全系数FS的均值方差,进而计算边坡的可靠度指标β及失效概率Pf。图1给出了基于无味变换的边坡可靠性分析方法的技术路线,其主要实施步骤:
1)分析选定对边坡可靠性更为敏感的参数作为随机变量,如通常将边坡土体的黏聚力c和摩擦角φ作为随机变量[11];
2)根据参数黏聚力c和摩擦角φ的均值、方差及相关系数ρcφ,计算得到随机变量的均值矩阵和协方差矩阵;
3)利用Step2得到的协方差矩阵进行平方根分解,并结合均值矩阵和引入的尺度参数,计算得到2n+1个σ点,见式(2)~式(7);
4)建立目标边坡计算模型,同时,将Step3得到的2n+1个σ点代入模型,并开展二维极限平衡计算,通过搜索最危险的滑面,得到2n+1个安全系数FS的值,见式(8);
5)利用权值的定义和λ、η等参数,分别得出2n+1个FS的均值和协方差的权值,见式(11)~式(13);
6)根据Step4得到的2n+1个FS值,并结合Step5计算得到的权值,分别借助式(9)、式(10)计算得到FS的均值和方差;
7)借助可靠度指标的定义(均值与标准差的比)直接计算边坡可靠度指标β值,同时,可借助失效概率与可靠度指标的关系进一步计算相应的失效概率。
2 算例分析
2.1 均质边坡算例
算例1为软土层上的均质边坡[17],典型剖面见图2,图中各层土体的参数见表1,且分布类型为正态分布[17-18]。借助Slide软件,采用简化的Bishop法进行极限平衡计算,得出坡体参数采用均值时的安全系数为1.165,安全系数与最危险滑面的位置均与Cho[18]计算(FS=1.164)非常接近。
在不考虑边坡土体黏聚力c和摩擦角φ的相关性时,根据表1土体参数黏聚力c和摩擦角φ的均值和方差,计算得到个9个σ点,并利用Slide开展二维极限平衡计算,从而得到9组安全系数,如表2所示,进而通过无味变换的边坡可靠度分析法得到算例1中边坡的失效概率为19.66%,与相应蒙特卡洛法(MCS)和一阶可靠度分析(FORM)验算点法得到的失效概率计算结果基本一致,相对误差在6%以内,如表3所示。
在考虑边坡土体抗剪强度参数间相关性时,表4为给出不同c和φ的相关系数ρcφ条件下分别采用无味变换法及蒙特卡洛(MCS)模拟得到的边坡失效概率。由于边坡主要的破坏模式(最危险滑面)均出现在土层1,土层2参数对于边坡稳定性及可靠度结果几乎没有影响,计算中土层2中c和φ的相关系数与土层1保持一致。综合表3和表4可知,在ρcφ由负到正的过程中,边坡失效概率明显增大,土体黏聚力c和摩擦角φ的相关性对坡体可靠性分析结果影响显著,这与一般结论相吻合[11,20]。
此外,表4还给出了以MCS的失效概率为基准值的当量比值R,其结果介于1.05~1.12之间,且随着c和φ的负相关性逐渐增强(ρcφ逐渐减小),R值逐渐增大,即无味变换法的相对误差δ(δ=|R-1|×100%)不断增大,而当c和φ呈现正相关关系时,R≤1.08,即相对误差均在8%以内。进一步分析可知,造成上述误差变化的主要原因在于失效概率量值的差异性,失效概率量值较大时,两种方法结果的差异性越不显著,反之,引起的相对误差较大。可见,本例中,在较低失效概率(Pf<15%)时,可靠性分析结果对计算方法的选擇比较敏感。
2.2 分层边坡算例
算例2为一个分层边坡,计算剖面见图3,边坡土层参数见表5,不确定参数服从正态分布[21]。采用抗剪强度参数均值,应用简化的Bishop法得出相应的坡体安全系数为1.509。
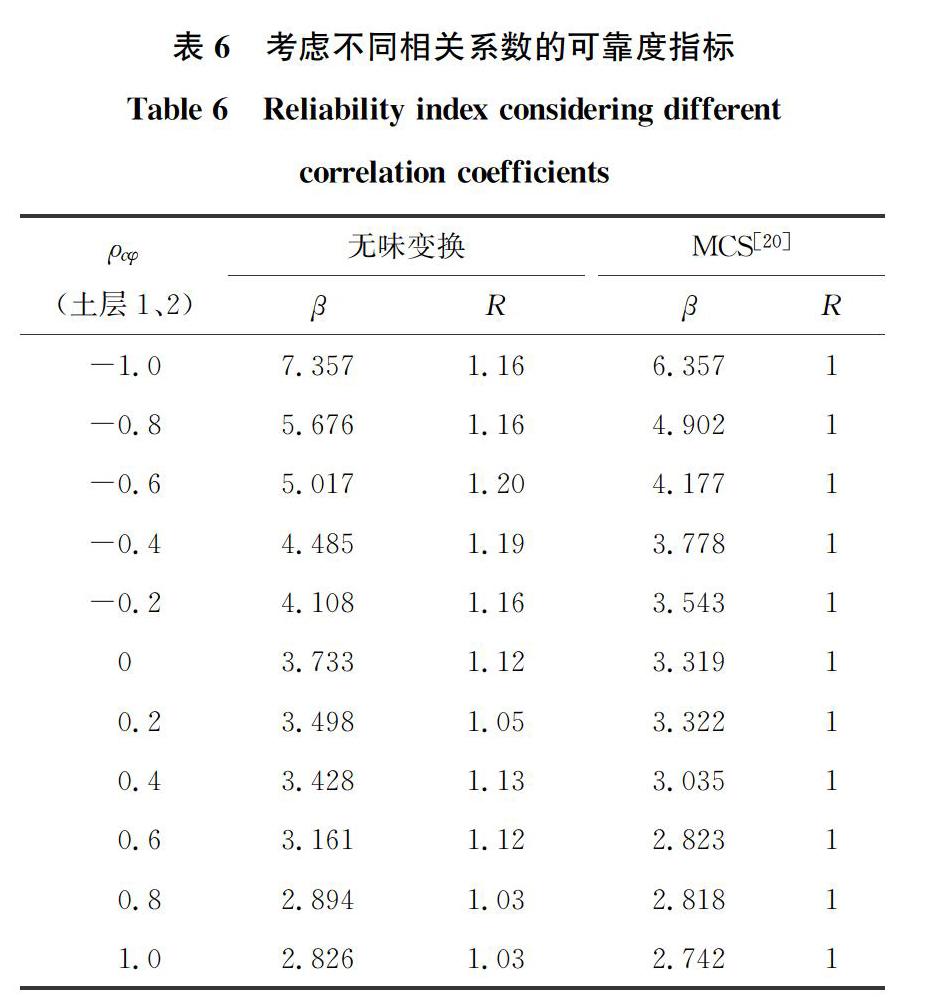
本例中,两层土坡共涉及抗剪强度参数黏聚力c和摩擦角φ等4个变量,依据表6中相关系数及各变量的均值和方差获取相应的均值矩阵及协方差矩阵,进而确定出9个σ点,得出基于无味变换的边坡可靠度指标β,见表6。
为分析两种方法结果的差异性,表6中还给出了以文献[21]中MCS得出的可靠度指标为基准值的当量比值R,同时,图4给出了无味变换与蒙特卡洛法[21](MCS)计算结果的对比。分析发现,ρcφ越小,(负相关性越显著)R值越大,β>3时,相对误差整体超过了10%,但进一步结合图4和表5分析发现,本例中坡体安全系数达到1.509,整体可靠度指标较大,特别是当ρcφ越小时,β越大,相应Pf更低,与算例1所述相同,说明较低失效概率易增加不同计算结果的差异性。
为进一步验证上述结论,通过不同程度地降低坡体土层c和φ的均值,即减小坡体安全系数,增大相应失效概率,得出了不同安全系数下无味变换法和MCS法的可靠度指标,见表7和图5。由表7和图5可见,边坡安全系数越小、可靠度越低时,相关系数的变化引起的误差波动越小,在β<1.5,即Pf>7%时,相对于MCS法,基于无味变化方法得出的误差均在5%以内,两种方法的计算结果差异性较小。
可见,相对于稳定性较好的边坡,基于无味变换的边坡可靠性分析方法能更好地应用于较低可靠度β<1.5(较高失效概率,Pf >7%)的坡体分析中,而该类边坡往往是工程中更为关注的对象,进而体现了所提出的基于无味变换的边坡可靠性分析方法的适用性。
3 计算效率分析
为了更好地说明基于无味变换的边坡可靠性分析方法的计算效率,从花费的计算时间角度分别对算例1和算例2进行了分析。基于无味变换的边坡可靠性分析的计算时间由3部分组成:利用Matlab计算得到σ点的用时,利用σ点开展二维极限平衡计算,得到安全系数和利用无味变换法进行失效概率计算的用时。对于算例1和2,表8给出了以上各部分计算用时及总时间情况。
同样,仍以蒙特卡洛法作为对比对象,由于该方法计算时间与计算精度均与抽样次数有关,一般需要进行20 000次以上的模拟才会收敛[22],同时,抽样次数越多,计算精度越高,但耗时更长。故分别选取20 000次(所需最少计算次数)和500 000次的蒙特卡洛模拟与无味变换方法进行计算时间对比,两种方法均考虑变量相互独立的情况,且均在配置内存为8 GB、处理器为Intel(R)Corei7、CPU主频为2.00 GHz的计算机上进行,计算用时结果如表9所示。显然,两个算例中,相对于蒙特卡洛模拟,无味变换方法用时更少,效率更高,对于最少计算次数(20 000次抽样)和较高精度(500 000次抽样)的蒙特卡洛模拟,算例1(均质边坡)中,无味变换法用时分别减少了17.9%和58.95%,而对于非均质边坡(算例2),无味变换法用时分别减少了8.21%和55.46%。
4 结论
1)基于无味变换的边坡可靠性分析方法应用方便,不依赖于变量的分布类型,能够显著提高计算效率,对于有n个主控随机变量的功能函数,只需2n+1次计算。
2)算例结果显示,在低失效概率时(Pf ≤7%),基于无味变换方法的计算结果误差达到5%以上,可靠性分析结果对计算方法的选择较为敏感,直接采用基于无味变换的方法会引起对可靠性结果过高的估计;但对于工程中关注更多的较高失效概率(Pf>7%)的边坡,基于无味變换方法计算结果相对误差在5%以内,且相关系数的变化引起的误差波动较小,适用性好。
3)借助无味变换原理丰富了边坡可靠性分析方法,但针对低失效概率条件下计算误差较大的内在机理以及如何实现较高计算精度的问题,还需从推求具有更佳逼近效果的σ点入手展开进一步的探索,期待提出的基于无味变换的边坡可靠性分析方法有更多的关注与发展。
参考文献:
[1] 苏永华, 赵明华, 蒋德松, 等. 响应面方法在边坡稳定可靠度分析中的应用[J]. 岩石力学与工程学报, 2006, 25(7): 1417-1424.
SU Y H, ZHAO M H, JIANG D S, et al. Application of response surface method to reliability analysis of slope stability [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1417-1424. (in Chinese)
[2] 许晓亮, 李建林, 龚家伟, 等. Copula理论下基于g-line失效域的边坡可靠性分析[J]. 岩土力学, 2017, 38(5): 1445-1453, 1462.
XU X L, LI J L, GONG J W, et al. Copula-based slope reliability analysis using g-line failure domain [J]. Rock and Soil Mechanics, 2017, 38(5): 1445-1453, 1462. (in Chinese)
[3] 李典庆, 周创兵. 考虑多失效模式相关的岩质边坡体系可靠度分析[J]. 岩石力学与工程学报, 2009, 28(3): 541-551.
LI D Q, ZHOU C B. System reliability analysis of rock slope considering multiple correlated failure modes [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 541-551. (in Chinese)
[4] 祝玉学, 沈大用. 可靠性指标法在双滑面破坏模式分析中的应用[J]. 矿山技术, 1989(3): 1-4.
ZHU Y X, SHEN D Y. Application of reliability index method in failure mode analysis of double sliding surface.[J]. China Mining Magazine, 1989(3): 1-4. (in Chinese)
[5] LOW B K. Efficient probabilistic algorithm illustrated for a rock slope [J]. Rock Mechanics and Rock Engineering, 2008, 41(5): 715-734.
[6] 郑智洋, 苏培东, 刘波,等. 基于双折减系数法的多滑面边坡稳定性分析方法研究 [J]. 工程地质学报, 2018, 26(Sup1):99-106.
ZHENG Z Y, SU P D, LIU B, et.al Study on the stability analysis method of multi slide slope based on double reduction coefficient method [J]. Journal of Engineering Geology, 2018, 26(Sup1):99-106. (in Chinese)
[7] 谭晓慧, 王建国, 刘新荣, 等. 边坡稳定的有限元可靠度计算及敏感性分析[J]. 岩石力学与工程学报, 2007, 26(1): 115-122.
TAN X H, WANG J G, LIU X R, et al. Finite element reliability computation and sensitivity analysis of slope stability [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 115-122. (in Chinese)
[8] JIMENEZ-RODRIGUEZ R, SITAR N. Rock wedge stability analysis using system reliability methods [J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 419-427.
[9] GRIFFITHS D V, HUANG J S, FENTON G A. Influence of spatial variability on slope reliability using 2-D random fields [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(10): 1367-1378.
[10] CHING J, PHOON K K, HU Y G. Efficient evaluation of reliability for slopes with circular slip surfaces using importance sampling [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(6): 768-777.
[11] 唐小松, 李典慶, 周创兵, 等. 基于Copula函数的抗剪强度参数间相关性模拟及边坡可靠度分析[J]. 岩土工程学报, 2012, 34(12): 2284-2291.
TANG X S, LI D Q, ZHOU C B, et al. Modeling dependence between shear strength parameters using Copulas and its effect on slope reliability [J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2284-2291. (in Chinese)
[12] LOW B K. Reliability analysis of rock slopes involving correlated nonnormals [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 922-935.
[13] 程水英. 无味变换与无味卡尔曼滤波[J]. 计算机工程与应用, 2008, 44(24): 25-35.
CHENG S Y. Unscented transformation and unscented Kalman filtering [J]. Computer Engineering and Applications, 2008, 44(24): 25-35. (in Chinese)
[14] 李胜全, 欧阳永忠, 常国宾, 等. 用无味变换法求解交会测量及其协方差传播[J]. 海洋测绘, 2012, 32(4): 38-40.
LI S Q, OUYANG Y Z, CHANG G B, et al. Solving intersection measurement problem and its covariance transformation using unscented transformation method [J]. Hydrographic Surveying and Charting, 2012, 32(4): 38-40. (in Chinese)
[15] SAVIN A A, GUBA V G, MAXSON B D. Covariance based uncertainty analysis with unscented transformation [C]//82nd ARFTG Microwave Measurement Conference, November 18-21, 2013. Columbus, OH, USA. IEEE, 2013.
[16] JULIER S J. The scaled unscented transformation [C]//Proceedings of the 2002 American Control Conference (IEEE Cat. No.CH37301), May 8-10, 2002. Anchorage, AK, USA. IEEE, 2002.
[17] CHOWDHURY R N, XU D W. Geotechnical system reliability of slopes [J]. Reliability Engineering & System Safety, 1995, 47(3): 141-151.
[18] CHO S E. First-order reliability analysis of slope considering multiple failure modes [J]. Engineering Geology, 2013, 154: 98-105.
[19] ZHANG J, HUANG H W, JUANG C H, et al. Extension of Hassan and Wolff method for system reliability analysis of soil slopes [J]. Engineering Geology, 2013, 160: 81-88.
[20] TANG X S, LI D Q, CHEN Y F, et al. Improved knowledge-based clustered partitioning approach and its application to slope reliability analysis [J]. Computers and Geotechnics, 2012, 45: 34-43.
[21] WU X Z. Probabilistic slope stability analysis by a copula-based sampling method [J]. Computational Geosciences, 2013, 17(5): 739-755.
[22] 吳振君, 王水林, 葛修润. LHS方法在边坡可靠度分析中的应用[J]. 岩土力学, 2010, 31(4): 1047-1054. WU Z J, WANG S L, GE X R. Application of Latin Hypercube Sampling technique to slope reliability analysis [J]. Rock and Soil Mechanics, 2010, 31(4): 1047-1054. (in Chinese)
(编辑 胡玲)
