考虑变形滞后效应的高液限土路基模量反算方法

刘闯　张锐　滕煜晟　任天锃　杨博

摘 要：为了提高便携式落锤弯沉仪（PFWD）测定高液限土路基回弹模量的精度，考虑变形滞后效应对反算结果的影响，提出了一种基于Kelvin粘弹性模型和准静态动力分析反算模量的方法。通过现场试验，验证了新方法的有效性。研究结果表明：利用高液限土填筑的下路堤模量较低，在PFWD冲击荷载作用下，其顶面竖向位移峰值明显滞后于荷载峰值，且荷载位移曲线非线性显著;基于线弹性模型的常规反算方法使得反算模量远大于实测模量，平均相对误差为52.5%;新方法能较好地反映冲击荷载作用下变形滞后特征，反算相对误差仅为9.2%。随着路基模量增大，路基变形滞后效应不显著，常规方法和新方法反算结果相近，但新方法反算结果的精度更高。

关键词：道路工程;粘弹性模型;准静态;模量反算;变形滞后;高液限土

中图分类号：U416.1;TU433   文献标志码：A   文章编号：2096-6717（2021）02-0068-08

Abstract： In order to improve the accuracy of Portable Falling Weight Deflectometer （PFWD） in measuring the resilient modulus of high liquid limit soil subgrade， the influence of deformation lags effect on the back-calculation result was considered and a new method for back-calculation of  the modulus was proposed based on Kelvin viscoelastic model and quasi-static dynamic analysis method. The effectiveness of the new method is verified by field tests. The results show that the measured modulus of the lower embankment filled with high liquid limit soil is lower and the peak vertical displacement of the top surface of the embankment obviously lags behind the peak value of the load under the impact load of PFWD. Furthermore， the load-displacement curve is significantly nonlinear. In addition， the conventional method based on linear elastic model makes the back-calculated modulus much larger than the measured modulus. The average relative error between back-calculated and the measured modulus reaches up to 52.5%. However， the new method can better reflect the deformation lag characteristics under impact load. The average relative error between them is only 9.2%. With increase of subgrade modulus， the lag effect of the deformation is not significant. The back-calculating results via conventional and new methods are similar， but the accuracy of the new method is higher.

Keywords：road engineering; viscoelastic model; quasi-static; modulus back-calculation; deformation lag; high liquid limit soil

高液限土在中國南方地区分布广泛，天然含水率高，水稳性差，用于公路路基填筑时，通常用作下路堤填料，并在湿法重型击实标准控制下压实。由于高液限土下路堤顶面回弹模量（以下简称模量）较低，需在其上部进行刚度补偿[1]，以达到路基顶面设计模量和验收弯沉值的要求。高液限土下路堤顶面模量的快速准确测定对于高液限土路基施工质量控制和刚度补偿设计至关重要。

现场测定路基模量的方法主要有承载板法、贝克曼梁法、落锤弯沉仪FWD法和便携式落锤弯沉仪PFWD法等。承载板法和贝克曼梁法耗时费力，所需测试人员多;FWD需专用车牵引，偏僻地方不宜到达，这3种方法多用于成型路基，难以用于路基施工质量控制[2]，虽然PFWD测试简便，但以往反算模量时仅取实测荷载和位移时程曲线的峰值，并假设路基为线弹性体，忽略了其他的时程数据和荷载位移的非线性[3-5]。对于冲击荷载作用下变形响应滞后且荷载位移非线性显著的路基，基于线弹性模型和静力分析方法反算的模量（简称常规反算模量）与承载板法直接实测的静模量（简称实测模量）相差较大[6]。有学者通过现场试验，建立了常规反算模量和实测模量的回归关系[7-8]，但现场检测工作量大，适用范围有限。学者们曾对FWD和PFWD冲击荷载作用下路基、路面非线性动力响应开展研究，有学者将变形滞后归因于弹性波传递时间，基于弹性动力学改进了常规反算方法，但仅将反算结果与基于线弹性模型的反算模量进行了对比[9-11]。也有学者将变形滞后归因于材料的粘弹性，基于粘弹性理论，改进了反算方法[12-18]，并提高了模量反算精度[19-23]，但主要针对路面多层模量反算，且多采用多参数复杂理论模型，若用于高液限土路基模量反算，将增加计算难度，也可能导致结果不收敛。

为解决PFWD常规反算中因理论假设与实际情况不符导致的反算高液限土路基模量与实测模量相差较大的问题，笔者基于粘弹性模型，采用准静态动力响应分析方法，提出并验证了既能反映高液限土路基非线性动力响应特征，又能用动载数据反算静力参数的高液限土路基模量反算新方法，编制了相应的反算程序。同时，将其应用于路基施工质量控制与刚度补偿设计。

1 高液限土路基模量现场试验

海南万宁至洋浦高速公路横贯海南岛，全长163 km，沿线开挖并用于路基填筑的高液限土约240万m3。在高液限土填方量较大的第六、第九和第十合同段，分别选取K67+190～K67+290 （WY-6）、K110+180～K110+280 （WY-9）和K121+460～K121+560 （WY-10）作为试验段。对试验段填料进行基本性质指标测试，结果如表1所示。由于高液限土天然含水率均远大于其最佳含水率，在海南多雨气候条件下，很难通过翻晒将高液限土填料含水率大幅降至最佳含水率压实。因此，在满足下路堤填料强度和变形要求前提下，在3个试验段均只将高液限土直接用作下路堤填料，在大于最佳含水率8%～10%状态下压实，并适当降低压实度控制标准[24]。

利用高液限土填筑下路堤后，分别在3个试验段下路堤顶面沿纵向每10 m一个测点，依次进行PFWD检测和承载板试验。使用的PFWD设备主要参数为：载荷板半径0.15 m，载荷范围1～15 kN，载荷脉冲形状为半正弦波;载荷传感器相对误差小于1%，绝对误差±0.1 kN;位移传感器有效测试精度1 μm，最大测试范围2 200 μm;数据采集周期0～60 ms。PFWD测试方法和步骤参照文献[2]进行。现场承载板试验参照《公路路基路面现场测试规程》（JTG E 60—2008）相关规定进行。

限于篇幅，仅列出3个试验段部分代表性PFWD试验结果，如图1所示。从图1（a）～（c）可以看出，3个测点PFWD荷载与竖向位移时程曲线均有相似性，当施加的荷载达到峰值时，该时刻对应的竖向位移并未达到峰值，变形未达到最大;当位移达到峰值时，荷载已处于减小阶段。从图1（d）可以看出，3个测点的荷载位移曲线表现出明显的非线性和滞回圈。因此，冲击荷载作用下高液限土填筑层变形滞后效应显著。

PFWD常规模量反算法是假设荷载与变形关系近似为线弹性，与承载板法一样，均采用圆形垂直刚性分布静荷载作用下的弹性半空间布辛尼斯克解（见式（1））计算路基模量。

E=πR2p（1-μ2）w（1）

式中：E为路基模量值，MPa;p为载荷板压力峰值，MPa;R为载荷板半径，m;μ为泊松比，取0.35;w为载荷板中心弯沉峰值，mm;π为圆周率。

由于冲击动荷载作用下变形存在滞后，且线弹性静力模型无法反映高液限土路基的非线性动力响应特征，若仍采用式（1）反算模量会造成结果的偏差。现场试验结果表明，图1（a）～（c）3个测点的常规反算模量分别为27.6、24.4、31.5 MPa，而实测模量分别为18.5、15.1、21.2 MPa。3个试验段30个测点的常规反算模量与实测模量如图2所示，统计的常规反算模量平均绝对误差10.9 MPa，平均相对误差52.5%。

2 基于粘弹性模型的模量反算方法

由于以往PFWD反算路基模量时采用的是线弹性静力学模型，而冲击荷载作用下高液限土路基具有显著变形滞后效应和荷载位移非线性特征，常规反算方法已不适用，因此，有必要建立一种可较好地反映冲击荷载作用下高液限土路基非线性动力响应特征的简便模量反算方法。

2.1 选用的粘弹性理论模型

众所周知，在正弦周期动荷载作用下，粘弹性材料的应变也呈周期变化，而且应变响应滞后于应力响应。粘弹性理论模型也普遍应用于行车荷载作用下沥青路面动力响应分析。考虑到冲击荷载作用下高液限土路基变形滞后效應与上述粘弹性材料力学行为相似，因此，基于粘弹性本构模型建立了高液限土模量反算新方法。

粘弹性模型中，Maxwell模型是由弹簧阻尼器串联而成，主要用于模拟粘弹性材料应力松弛过程。三参量固体模型、Burgers模型和广义Maxwell模型等是用弹簧阻尼器并联和串联多种形式构造出的更加复杂的力学模型，可以描述动荷载作用下材料的粘弹性以及残余变形性质。而PFWD测试时，会通过多次落锤消除测点的塑性变形，因此，反算高液限土路基模量不需考虑残余变形，不必采用形式复杂的多参数粘弹性模型增加反算难度。

Kelvin模型是由弹簧阻尼器并联构成的粘弹性模型[11]。该模型形式简洁，便于高效地迭代运算。其数学描述见式（2）。

根据式（3）可得到加卸载作用下的应力应变曲线，如图3所示。由图3可以看出，当引入粘滞系数后，加载时应力首先增至最大值，应变随后增至最大值，应变具有滞后性，应力应变曲线形式与图1（d）所示的PFWD实测荷载位移曲线形式极为相似。因此，选用Kelvin模型用于冲击荷载作用下高液限土路基动力响应分析。

2.2 准静态反算方法

动态法和准静态法[15，26]是动荷载作用下弹性体系动力响应分析的两种方法。

动态法反算[27]是将Navier动力方程中引入粘弹性理论模型，通过Laplace和Hankel反算导出竖向位移的显式解，并考虑复杂混合边值问题反算模量。由于反算时隐式偏微分方程结构较复杂，需采用诸多简化数值算法进行，比较耗时。

采用准静态法反算思路是将静荷载作用下弹性半空间体表面的竖向位移显式解作Laplace变换，并将变换式中的弹性参数代之以粘弹性算子再作反算。这种方法可用动载数据反算静力参数。后续的结果也验证了对于高液限土路基采用准静态法进行反算，其结果精度能够满足要求。因此，采用该方法和PFWD动载数据反算的模量属于静模量，从而与承载板法测得的静模量在类型上保持一致。

式中：w（r，t）为PFWD刚性载荷板作用下粘弹性半空间体表面竖向位移，mm;L-1（w-（r，s））为竖向位移的拉普拉斯反变换;E（s）=E+ηs为粘弹性算子，η为粘滞系数;E和μ的意义同式（1）;F为PFWD落锤时作用于测点表面的集中力，kN，由荷载时程曲线得到;R和r的意义同式（4）;s为时间t的Laplace变换参量。

由式（5）可知，当t=0时，竖向位移为0;当t趋近于无穷时，竖向位移等于传统弹性半空间理论计算得到的竖向位移。粘滞系数η所在的项，随着时间的变化是一个始终大于0小于1的数，限制了整体竖向变形，使理论计算位移时程的峰值缩小和相位向右延展。

2.3 模量反算程序的编制

由式（5）的形式可知，反算参数为模量值E和粘滞系数η。因式（5）比较复杂，难以得到反算参数的解析解，故采用最小二乘法，即式（6）迭代求极值的优化算法进行反算。

由于基于最小二乘优化算法得到的是采用函数定义域内全局求极值的反算结果，该反算结果可能与实际情况相差较大，因此，在编制反算程序时，针对PFWD检测高液限土路基模量的具体情况作了如下处理：由于数据采集周期0～60 ms内落锤会在橡胶块上振动，进而带动承载板产生小幅跳动，故只取0～25 ms内峰值波形的数据;计算点位r=0 m，即荷载作用面表面的中心处;精度控制参数K=0.5和迭代控制系数ε=0.01，两个控制值可按照不同精度要求进行调整。

进行反算时还需要将式（8）进行变形得到式（11），以控制反算模量值的权重。当计算位移时程的相位大于实测位移时程或计算位移峰值小于实测值，但迭代还未满足式（9）的要求时，停止参数η的迭代，而继续进行参数E的迭代。

按照上述方法，利用Matlab編写了考虑冲击荷载作用下变形滞回效应的高液限土路基模量反算程序[28]，既适用于FWD反算，也适用于PFWD反算。反算流程如图4所示。

3 模量反算新方法的验证与应用

根据图1所示3个测点的PFWD荷载和位移时程曲线，利用本文提出的基于粘弹性模型的高液限土路基模量反算方法（简称新方法）进行了模量反算，并与常规方法的反算结果和实测结果进行了对比，如表2所示。3个测点的反算结果表明，新方法反算的模量仅比相应的实测模量大2 MPa左右，而常规反算模量比实测模量要大10 MPa左右，新方法的模量反算精度提高了40%左右。

分别利用新方法和常规方法反算得到的模量正算位移时程，并与实测位移时程进行对比。其中，图5为测点K110+200位移时程曲线对比结果。由图5可以看出，基于粘弹性模型的新方法计算得到的位移时程与实测位移时程非常吻合。根据式（13），新方法的计算精度系数则为0.935，常规方法得到的精度系数仅为0.693。K110+200和K121+500精度系数对比结果相似，一同列于表2。以上位移时程与精度系数对比结果表明，引入粘弹性模型后，新方法能较为准确地反映冲击荷载作用下高液限土路基变形响应滞后这一特征。

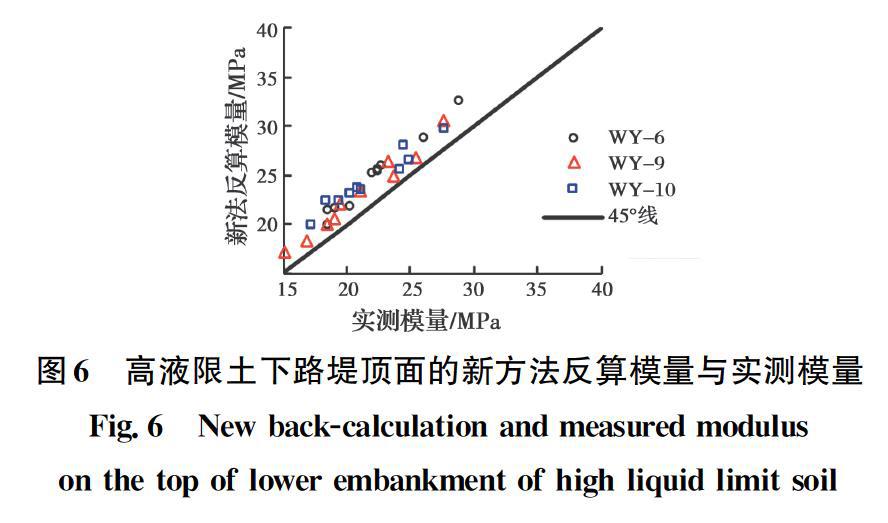
按照新方法对3个试验段30个测点进行模量反算的结果如图6所示。对比图2可看出，新方法反算模量相对常规反算模量更接近实测模量，平均绝对误差仅为2.6 MPa，平均相对误差为9.2%。同时也证明了，由于采用了准静态分析方法，可根据冲击荷载作用下路基动力响应（荷载和位移时程数据）反算静力参数，从而使得新方法反算模量更接近由承载板法实测的静模量。

良好的路基施工质量必然要求在各层位施工完成后路基强度变异性小，均匀一致[29]。为此，应用PFWD和模量反算新方法，对海南万洋高速公路高液限土下路堤顶面模量的变异性进行了评价，快速、准确地确定了模量过低需要补压处理的点位，减小了下路堤模量的变异性。由于高液限土下路堤模量较低，而万洋高速公路路基顶面设计弯沉值为120（0.01 mm），需要在上路堤和路床填筑合适填料进行刚度补偿。为此，采用文献[2]的方法，继续以WY-9为试验段，进行了路基刚度补偿设计和现场试验，确定并实施了用高液限土掺30%砂砾填上路堤，用高液限土掺40%砂砾填下路床，用低液限土掺4%水泥填上路床方案。实测路基弯沉的代表值为88（0.01 mm），满足验收要求。

为研究新方法对于高模量路基测试的适用性，在WY-9试验段路基顶面分别进行了PFWD与承载板试验。其中，K110+200处PFWD测试结果如图7所示。与图1（b）、（d）相比，由于路基模量提升，冲击荷载作用下变形滞后效应和荷载位移滞回圈虽显著减小，但仍然存在，同样会导致常规反算误差。承载板实测与PFWD模量反算结果表明：实测模量为196.1 MPa，常规反算模量为221.10 MPa，新方法反算模量为205.6 MPa。

图8为WY-9试验段路基顶面所有10个测点的模量实测与反算结果。统计结果表明：新方法反算模量平均绝对误差为8.5 MPa，平均相对误差仅为4.3%;而常规反算模量平均绝对误差为24.1 MPa，平均相对误差为12.2%。可以看出，当路基模量较高时，新方法和常规方法反算模量的平均相对误差均有所减小，但新方法反算结果的精度更高。

根据高液限土路基试验段现场试验结果，由于在低模量的下路堤和高模量的路床顶面新方法反算模量与实测模量之间的相对误差均在10%以内，因此，可将新方法反算的模量直接作为高液限土路基刚度补偿设计的参数。

4 结论

1）冲击荷载作用下高液限土路基变形峰值滞后于荷载峰值，荷载位移曲线弹性滞回明显。

2）基于线弹性静力模型的PFWD模量常规反算方法忽略了路基非线性动力响应特征，用于高液限土路基模量测定时，反算模量与实测模量偏差较大。

3）基于粘弹性模型和准静态法的PFWD模量反算新方法既可反映路基非线性动力响应特征，又可用动载数据反算静模量;在下路堤和路床顶面，采用新方法反算的模量均与实测模量接近，误差在10%以内。

4）模量反算新方法可用高液限土路基各层位顶面模量变异性控制，建议将新方法反算模量作为路基刚度补偿的设计参数。

参考文献：

[1] 郑健龙， 张锐. 公路膨胀土路基变形预测与控制方法[J]. 中国公路学报， 2015， 28（3）： 1-10.

ZHENG J L， ZHANG R. Prediction and control method for deformation of highway expansive soil subgrade [J]. China Journal of Highway and Transport， 2015， 28（3）： 1-10. （in Chinese）

[2] 查旭东. PFWD快速检测路基模量研究[J]. 公路交通科技， 2009， 26（1）： 26-30.

ZHA X D. Study of rapid test of subgrade modulus with PFWD [J]. Journal of Highway and Transportation Research and Development， 2009， 26（1）： 26-30. （in Chinese）

[3] NAZZAL M D， MOHAMMAD L N. Estimation of resilient modulus of subgrade soils using falling weight deflectometer [J]. Transportation Research Record， 2010， 2186（1）： 1-10.

[4] PIERCE L M， SMITH K D， BRUINSMA J E， et al. Case studies using falling weight deflectometer data with mechanistic-empirical design and analysis[M]// Pavement Performance： Current Trends， Advances， and Challenges. 100 Barr Harbor Drive， PO Box C700， West Conshohocken， PA 19428-2959： ASTM International， 2012： 1-14.

[5] 張军辉， 彭俊辉， 郑健龙. 路基土动态回弹模量预估进展与展望[J]. 中国公路学报， 2020， 33（1）： 1-13.

ZHANG J H， PENG J H， ZHENG J L. Progress and prospect of the prediction model of the resilient modulus of subgrade soils [J]. China Journal of Highway and Transport， 2020， 33（1）： 1-13. （in Chinese）

[6] 梁新政， 王复明， 孔宪京. 路基模量反演结果分析[J]. 岩土工程学报， 2000， 22（5）： 619-621.

LIANG X Z， WANG F M， KONG X J. Analysis for result of subgrade modulus backcalculation [J]. Chinese Journal of Geotechnical Engineering， 2000， 22（5）： 619-621. （in Chinese）

[7] 段丹军， 查旭东， 张起森. 应用便携式落锤弯沉仪测定路基回弹模量[J]. 交通运输工程学报， 2004， 4（4）： 10-12.

DUAN D J， ZHA X D， ZHANG Q S. Subgrade resilience modulus measuring by portable falling weight deflectometer（PFWD） [J]. Journal of Traffic and Transportation Engineering， 2004， 4（4）： 10-12. （in Chinese）

[8] 杨博， 张锐， 查旭东， 等. 一种路基动模量测试方法[J]. 岩土力学， 2014， 35（5）： 1514-1519.

YANG B， ZHANG R， ZHA X D， et al. A method for testing dynamic mouduli of subgrade [J]. Rock and Soil Mechanics， 2014， 35（5）： 1514-1519. （in Chinese）

[9] 查旭东， 袁盛杰， 肖秋明. 冲击荷载作用下的路基动力反算[J]. 长沙理工大学学报， 2014， 11（4）： 1-7， 14.

ZHA X D， YUAN S J， XIAO Q M. Subgrade dynamic backcalculation under impact loading [J]. Journal of Changsha University of Science & Technology， 2014， 11（4）： 1-7， 14. （in Chinese）

[10] LIU X L， ZHANG X M， WANG H， et al. Laboratory testing and analysis of dynamic and static resilient modulus of subgrade soil under various influencing factors [J]. Construction and Building Materials， 2019， 195： 178-186.

[11] HAMIM A， YUSOFF N I M， CEYLAN H， et al. Comparative study on using static and dynamic finite element models to develop FWD measurement on flexible pavement structures [J]. Construction and Building Materials， 2018， 176： 583-592.

[12] LI M Y， WANG H. Prediction of asphalt pavement responses from FWD surface deflections using soft computing methods [J]. Journal of Transportation Engineering， Part B： Pavements， 2018， 144（2）： 04018014.

[13] LI M Y， WANG H， XU G J， et al. Finite element modeling and parametric analysis of viscoelastic and nonlinear pavement responses under dynamic FWD loading [J]. Construction and Building Materials， 2017， 141（1）： 23-35.

[14] ZHANG J H， PENG J H， LIU W Z， et al. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction [J]. Road Materials and Pavement Design， 2019， 2019（1）： 1-13.

[15] 鄭传超. 道路结构力学计算[M]. 北京： 人民交通出版社， 2003.

ZHENG C C. Mechanical calculation of road structure [M]. Beijing： China Communications Press， 2003. （in Chinese）

[16] 曹丹丹， 赵延庆， 田泽峰， 等. 沥青路面动态黏弹反演研究[J]. 土木工程学报， 2017， 50（9）： 104-109.

CAO D D， ZHAO Y Q， TIAN Z F， et al. Back-calculation study on asphalt pavement using dynamic viscoelastic method [J]. China Civil Engineering Journal， 2017， 50（9）： 104-109. （in Chinese）

[17] GRASMICK J G， MOONEY M A， SENSENEY C T， et al. Comparison of multiple sensor deflection data from lightweight and falling weight deflectometer tests on layered soil [J]. Geotechnical Testing Journal， 2015， 38（6）： 20140172.

[18] SIRITHEPMONTREE H， SAPSATHIARN Y. Dynamic soil models for backcalculation of material properties from falling weight deflectometer deflection data [J]. Procedia Engineering， 2017， 189： 152-157.

[19] ZHANG J H， GU F， ZHANG Y Q. Use of building-related construction and demolition wastes in highway embankment： Laboratory and field evaluations [J]. Journal of Cleaner Production， 2019， 230： 1051-1060.

[20] ASLI C， FENG Z Q， PORCHER G， et al. Back-calculation of elastic modulus of soil and subgrade from portable falling weight deflectometer measurements [J]. Engineering Structures， 2012， 34： 1-7.

[21] BENEDETTO A， TOSTI F， DI DOMENICO L. Elliptic model for prediction of deflections induced by a Light Falling Weight Deflectometer [J]. Journal of Terramechanics， 2012， 49（1）： 1-12.

[22] NEGA A， NIKRAZ H， AL-QADI I L. Dynamic analysis of falling weight deflectometer [J]. Journal of Traffic and Transportation Engineering （English Edition）， 2016， 3（5）： 427-437.

[23] ZHANG J H， PENG J H， ZENG L， et al. Rapid estimation of resilient modulus of subgrade soils using performance-related soil properties [J]. International Journal of Pavement Engineering， 2019（1）： 1-8.

[24] 張锐， 肖宇鹏， 刘闯， 等. 考虑吸附结合水影响的高液限土路基压实度控制标准[J]. 中国公路学报， 2020， 33（1）： 32-40， 50.

ZHANG R， XIAO Y P， LIU C， et al. Control standards for degree of compaction of high liquid limit soil subgrade considering effects of adsorbed bound water [J]. China Journal of Highway and Transport， 2020， 33（1）： 32-40， 50. （in Chinese）

[25] 谢定义. 土动力学[M]. 北京： 高等教育出版社， 2011.

XIE D Y. Soil dynamics[M]. Beijing： Higher Education Press， 2011.（in Chinese）

[26] 郭大智， 任瑞波. 层状粘弹性体系力学[M]. 哈尔滨： 哈尔滨工业大学出版社， 2001.

GUO D Z， REN R B. Layered viscoelastic system mechanics [M]. Harbin： Harbin Institute of Technology Press， 2001.（in Chinese）

[27] 杨博， 郑健龙， 查旭东. 刚柔复合式路面动测评价方法与试验研究[J]. 中国公路学报， 2015， 28（5）： 77-86.

YANG B， ZHENG J L， ZHA X D. Dynamic testing evaluation method and experimental research for rigid-flexible composite pavement [J]. China Journal of Highway and Transport， 2015， 28（5）： 77-86. （in Chinese）

[28] 张锐， 滕煜晟， 刘闯， 等. 基于FWD的细粒土路基模量反算软件[CP]. 2018.

ZHANG R， TENG Y S， LIU C， et al. Software for calculating modulus of fine soil subgrade based on FWD [CP]. 2018.（in Chinese）

[29] 李跃军， 吴亚中， 李亮. 基于可靠度的路基均匀性评价标准[J]. 交通运输工程学报， 2010， 10（3）： 17-22.

LI Y J， WU Y Z， LI L. Uniformity evaluation standard of subgrade based on reliability [J]. Journal of Traffic and Transportation Engineering， 2010， 10（3）： 17-22. （in Chinese）

（编辑 王秀玲）