基于GAN的通信干扰波形生成技术

赵 凡, 金 虎

(国防科技大学电子对抗学院, 安徽 合肥 230037)

0 引 言

通信干扰是通信对抗领域的一个重要研究方向,在通过通信侦察手段获取目标信号的工作频率、调制方式、调制参数等信息的基础上,通信干扰系统通过产生与目标信号相关联的干扰信号,对目标信号的通信过程进行压制和破坏,最终达到削弱甚至阻断对方通信能力的目的。

在实际的对抗过程中,干扰方在获取目标信号特征的先验知识后,目前主要依靠从固定的干扰策略库中或凭借用户经验制定干扰策略,并从平时所积累的大数据样本中选取干扰波形。当没有关于目标信号的先验知识,或目标信号参数动态变化时,干扰方无法自适应地调整干扰策略。与之相对的是,近年来人工智能领域蓬勃发展,越来越多的智能技术被用到通信系统中[1-3],通信系统的智能化水平不断提高,能够自主感知到电磁环境的变化并快速做出应变,抗干扰能力显著提升。因此,为了应对智能化水平越来越高的通信系统,干扰方也在不断尝试提高自身的智能化水平[4-6]。利用遗传算法[7]、博弈论[8-10]、强化学习[11-12]等方法代替人工搜寻最优干扰策略[13],但上述方法实现的前提是知道关于目标信号的先验知识或者能获得干扰反馈信息,并且多数方法只能针对固定干扰任务,当目标信号参数动态变化时,上述方法仍然难以发挥作用。生成对抗网络(generative adversarial networks,GAN)的兴起为解决这个问题提供了新的思路。

受博弈论的影响,GAN[14]由两个互相博弈的网络组成,生成网络试图生成逼近真实样本分布的数据去骗过判别网络,而判别网络则试图正确判断输入的来源,在相互博弈中,两者逐渐提升各自的生成能力和判别能力。博弈的最终结果是两者达到纳什均衡,生成网络学到了训练集中真实样本的分布,能生成逼真的样本骗过判别网络。而在通信干扰中,干扰方所用的干扰信号与目标信号的关联性越大,干扰效果越好。这与GAN中生成网络的目标相似,生成网络生成的样本越逼真就越能骗过判别网络,通信干扰中所用的干扰波形与目标信号的关联性越大,就越有可能落入目标信号的信道中,进入目标通信系统的接收机,对目标通信系统造成干扰。

因此,本文将GAN运用到通信对抗领域中,提出一种基于GAN的通信干扰波形生成技术,运用GAN自主对采集到的目标信号时域波形进行学习,获取目标信号的潜在分布,并生成逼近目标信号分布的干扰波形,对目标通信系统施加干扰。本文在分析GAN基本原理的基础上,首先针对通信信号的特点,设计网络模型,并优化学习率,使得训练数据为通信信号时域波形时,网络能够快速收敛,生成与目标信号高度关联的干扰波形;其次,通过对不同类型和参数的通信信号进行干扰波形生成实验,来验证该技术的泛化性;最后,与最佳干扰和噪声干扰效果进行性能对比试验。

1 基于GAN的通信干扰波形生成

对数字通信系统进行干扰主要有3个可行途径:对信道的干扰、对同步系统的干扰和对传输信息的干扰。其中,对信道的干扰是针对解调器的特点所施加的干扰,要求干扰信号与目标信号在信号层面是相似的,也就是要求干扰信号与目标信号具有相近的时域、频域、调制域特性,这样干扰信号就能够与通信信号一起进入解调器的输入端,扰乱解调器的门限判决过程,使判决出错,误码率(bit error rate,BER)增加。本文基于GAN所生成干扰波形就是用于针对信道进行干扰。

1.1 GAN

GAN由两个相互对抗的网络——生成网络G和判别网络D组成,其基本结构如图1所示。G的输入是随机噪声矢量z,其目标是生成分布尽可能逼近真实样本分布的伪数据G(z)去骗过D;D的输入是训练集中的真实样本x或者G生成的伪数据G(z),其目标是尽可能正确的判断输入的来源。D的输出是一个标量,用来表示判定输入是真实样本的概率,当D认为输入是真实样本时,输出1,当D认为输入是G生成的伪数据G(z)时,输出0。

图1 GAN基本结构

D和G可以是任意可微函数,在实际的训练过程中,我们通常采用随机梯度下降法交替对D和G进行优化。对D进行优化时,要固定G的参数,由于D的目标是实现对输入数据的二分类,也即输入为真实数据x时,输出1,输入是伪数据G(z)时,输出0,其损失函数可以用交叉熵函数描述为

(1)

式中,第1项中的D(x)表示输入是真实样本x时,D判决输入是真实样本的概率;第2项中的D(G(z))表示输入是G生成的伪数据时,D判决输入是真实样本的概率。优化D的过程就是运用随机梯度下降法调整D的网络参数使得J(D)最小化的过程。

同理,优化G时,需要固定D的参数。G的目标是用生成的G(z)来骗过D,也即希望D(G(z))趋近于1,J(D)的第二项越小越好,因此G的损失函数可以描述为

(2)

因此,优化G的过程就是运用随机梯度下降法调整G的网络参数使得J(G)最小化的过程。并且,由于优化G时,不需要用到真实样本,总体上GAN的目标函数可以描述为

Ez～pz(z)[log(1-D(G(z)))]

(3)

因此,由式(3)可以看出,GAN的优化过程就是G和D进行极大极小博弈的过程。训练时,先固定G的参数,以真实样本x和G生成的伪数据G(z)为训练集对D进行训练,使目标函数V(D,G)最大化,也即使D具有一定的判别能力;再固定D的参数,优化G,使目标函数V(D,G)最小化,也即提高G的生成能力。上述过程交替进行,最终当G的生成能力优化到能够生成以假乱真的伪数据去骗过D,而D无法判断出输入的来源,输出逼近某个固定值时,便认为G已经掌握了训练集中真实样本的分布,能够生成“逼真”的样本。

1.2 网络模型设计

本文实验中,直接对目标信号时域波形进行采样,1 000个点为一个样本,得到长度为1 000的一维时间序列数据作为真实数据x输入到判别网络中去。由于本文所处理数据为一维时间序列数据,结构简单,并且与二维图像相比,通信信号所蕴含特征更少,更易理解,因此在搭建网络时没有采用卷积层和反卷积层来提取特征和拟合数据的分布,而是直接用全连接层加激活函数来实现[15],本文所搭建的GAN的基本结构如图2所示。生成网络与判别网络都只含有一个隐藏层,并且隐藏层和输出层都用全连接层加激活函数实现。

图2 本文所用GAN结构

如图2(a)为生成网络的结构示意图,输入是长度为100的一维的随机噪声,经过两层全连接层转换成长度为1 000的干扰波形输出,其中隐藏层的激活函数为Relu,输出层的激活函数为Tanh。如图2(b)为判别网络的结构示意图,判别网络的结构与生成网络相反,输入是长度为1 000的目标信号时域采样数据或者生成网络输出的干扰波形,经过两次全连接层的变换,输出一个标量,表示判定输入是目标信号的概率,其中隐藏层的激活函数为Relu,输出层的激活函数为Sigmoid。

1.3 通信干扰波形生成

搭建GAN和调制方式为二进制相移键控(binary phase shift keying,BPSK)、正交相移键控(quadrature phase shift keying,QPSK)、16进制正交幅度调制(16 quadrature amplitude modulation,16QAM)、二进制频移键控(binary frequency shift keying,2FSK)的通信系统,采集通信信号制作训练集,对GAN进行训练。在训练过程中,考虑到损失函数只能够反映出网络生成能力和判别能力的变化,并不能直观、准确地衡量所生成干扰波形与训练集中目标信号时域波形的关联性,本文对生成波形做傅里叶变换,观察分析其频域特性,并与时域特性、损失函数一起作为衡量所生成波形优劣的标准。接下来对学习率进行优化,使网络能够迅速收敛,生成与目标信号高度关联的干扰波形。最后运用生成的干扰波形对目标通信系统施加干扰,并与最佳干扰、噪声干扰的干扰效果相比较,来验证本文通信干扰波形生成技术的有效性。本文主要算法架构如图3所示。

图3 基于GAN的通信干扰波形生成技术框图

本文算法主要步骤如下。

步骤 1采集BPSK、QPSK、16QAM、2FSK信号时域波形,以10个码元,1 000个采样点为一个样本,每种信号产生128 000个样本,制作多个训练集。

步骤 2分别用几种信号的训练集对GAN进行训练,当损失函数变化趋势趋于稳定,生成波形具有与训练集中信号相似的时域、频域特性时,停止训练,并输出生成波形。

步骤 3更改学习率,多次进行训练,选取最优的学习率实现通信干扰波形的生成。

步骤 4运用所生成的干扰波形对目标通信系统施加干扰,并与最佳干扰、噪声干扰的干扰效果进行对比。

2 实验结果与分析

为了验证本文干扰波形生成技术的可行性,进行了学习率的优化实验、网络的应用泛化性实验和干扰效果对比实验。

硬件设备环境:Window 10系统,NVIDIA GeForce GTX 1660Ti显卡和TensorFlow1.14.0框架。

2.1 实验1——学习率优化实验

目前GAN多运用在计算机视觉领域[16-20],用于处理特征复杂的二维图片数据,而本文需要用GAN来处理特征相对二维图片更简单的一维时间序列数据。数据维度和特征的变化,使得所需要的学习率也不同。因此,首先以BPSK信号为例,进行了学习率的优化实验,选取合适的学习率用于实现通信信号的生成。仿真时,参数设置:BPSK信号载波频率为4 000 Hz,采样频率为80 000 Hz,码元速率为800 Hz,发送“1”时,初始相位为π/4,发送“0”时,初始相位为-3π/4,以10个码元,1 000个采样点为一个样本,共128 000个样本为一个训练集,批次处理大小为256。

将学习率分别设置为0.000 1,0.001进行实验,训练次数从1 000次到90 000次,损失函数变化曲线如图4所示。

图4 学习率为0.000 1和0.001时损失函数

从图4中可以看到,由于两个网络在相互对抗,因此无论总体变化趋势如何,两个网络的损失函数都处于剧烈震荡中。当学习率为0.000 1时,从总体趋势上看,训练初期判别网络的损失函数呈下降趋势,而生成网络的损失函数呈上升趋势,表明判别网络的判别能力在提升,而生成网络的生成能力较弱,无法生成逼近真实分布的波形来骗过判别网络。随着训练次数的增多,判别网络的损失函数在短暂的上升之后持续下降并趋于稳定,而生成网络的损失函数在短暂的下降之后持续上升并趋于稳定,表明随着训练次数的增多,判别网络判别能力迅速提升,而生成网络的生成能力提升速度较慢,生成的样本无法骗过判别网络。

而在学习率为0.001时,初期判别网络与生成网络的损失函数波动都比较大,在短暂的上升之后迅速下降并趋于稳定,这表明训练初期,两者能力相当,在相互对抗中各自的判别能力和生成能力都在提升。后期判别网络的损失函数呈上升趋势并趋于稳定,生成网络的损失函数呈下降趋势并趋于稳定,表明随着训练次数的增加,生成网络的生成能力逐渐提升,并且提升速度较快,逐渐能够生成逼真的样本去骗过判别网络,判别网络无法正确判断出输入数据的来源,输出趋于某个固定值。

从损失函数的变化趋势来看,学习率为0.001时生成网络生成能力的提升速度比学习率为0.000 1时更快更好,因此尝试将学习率取的更大,观察损失函数的变化趋势。学习率为0.01时,训练次数从1 000次到90 000次,损失函数变化曲线如图5所示。

图5 学习率为0.01时损失函数变化图

考虑到学习率为0.01时,损失函数变化趋势差别较大,因此多次对网络进行训练,取较典型的3次数据作图5。从图5(a)中可以看到,判别网络的损失函数在短暂波动之后,迅速趋于0,无法提供梯度供生成网络更新,生成网络的梯度消失了,生成能力无法再提高。这表明学习率取值过大,以至于参数在最优解附近来回震荡,无法收敛。

总的来说,从两个网络的损失函数变化趋势来看,学习率为0.001时网络的生成能力提升较快,经过训练后网络能够迅速收敛。接下来,进一步通过分析不同学习率时网络所生成样本的时域波形图、频谱图来更加直观地衡量网络所生成干扰波形的优劣。图6为不同学习率时GAN所生成样本的时域波形图和频谱图。

图6 不同学习率时生成样本的时域波形图和频谱图

图6(a)中从上到下依次为学习率为0.000 1,0.001,0.01时GAN所生成样本的时域波形图,左侧为该学习率下训练2 000次之后所生成的样本,右侧为训练90 000次之后所生成的样本,图6(b)中对应位置为其频谱图。从图6中可以看出,学习率为0.001时,GAN训练速度最快,生成能力最强,在训练2 000次后生成网络所生成样本已经有较为明显的与目标信号相似的频域特性,并且在训练90 000次后生成样本与目标信号时域特性、频域特性相似度更高。而学习率为0.01时,虽然训练2 000次后生成的样本与目标信号有较为相似的频域特性,但之后生成网络的生成能力没有明显提高,训练90 000次后所生成样本与目标信号的相似度仍与训练2 000次后相当。学习率为0.000 1时,生成网络的生成能力提高的速度明显比学习率为0.001和0.01时更慢,在训练2 000次后,所生成样本仍没有明显的特征,但随着训练次数的增加,生成能力在不断提升,训练90 000次后所生成样本已经与目标信号具有较为相似的时域特性和频域特性,但相似度与学习率为0.001时差别较大,说明学习率为0.000 1时,生成网络的生成能力虽然能随着训练次数的增加而不断提升,但提升速度较慢。总的来说,学习率取0.001时,网络生成能力提升较快,能够较快地生成与目标信号具有相似时域特性和频域特性的干扰波形。

2.2 实验2——网络的应用泛化性实验

传统干扰方法是基于已经侦察到的目标信号特征,来选择合适的干扰波形实施干扰,而本文提出的基于GAN的通信干扰波形生成技术,直接运用GAN对采集到的目标信号时域波形进行学习,获取其潜在特征,并生成与之具有相似特征的波形作为干扰波形,不需要关于目标特征的先验知识,与传统干扰方法相比泛化性更强。下面对GAN在不同目标通信信号上的应用效果做实验探究,验证其泛化性。

实验1中对BPSK信号时域波形进行采样制作数据集,对网络进行训练。为说明GAN对其他类型通信信号也有较好的生成效果,分别取QPSK,16QAM,2FSK信号时域波形制作数据集,对网络进行训练。

实验所用QPSK信号载波频率为2 400 Hz,发送“11”时,初始相位为π/4,发送“01”时,初始相位为3π/4,发送“00”时,初始相位为5π/4,发送“10”时,初始相位为7π/4。在网络结构不变的情况下,学习率设置为0.001,批处理大小为256,以QPSK信号数据集对网络进行训练,训练次数从1 000次到90 000次,损失函数变化曲线如图7所示。

图7 QPSK信号损失函数变化图

从图7中可以看到,在训练初期,生成网络和判别网络的损失函数变化均较大,在训练40 000次之后,生成网络和判别网络的损失函数均趋于稳定,网络能够迅速收敛。以10个码元为例,训练90 000次后所生成样本时域波形图和频谱图如图8所示。

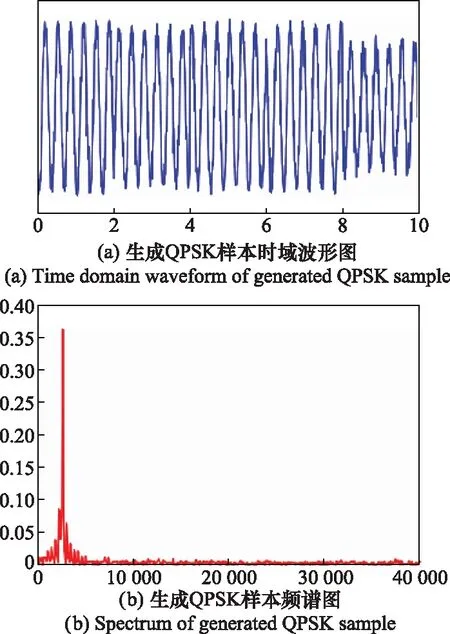
图8 生成QPSK样本时域波形图和频谱图

图8(a)为生成QPSK样本的时域波形图,可以看到,网络学习到了QPSK信号相位翻转的特征,在图8(a)中,2,4,6,8码元交界处出现了相位翻转。图8(b)为生成QPSK样本的频谱图,与训练所用QPSK信号载波频率一致,表明网络学习到了QPSK信号的频谱特征。

BPSK、QPSK均通过载波信号的相位变化来携带信息,而正交振幅调制同时运用载波信号的幅度和相位来携带信息,是目前通信系统中较为常用的调制方式。与BPSK、QPSK信号时域波形相比,QAM信号时域波形同时具有相位和幅度的变化。实验中,运用正交调幅法,将两路独立的正交4ASK信号叠加起来得到16QAM信号。两路4ASK信号的4个振幅均设置为-1,-0.34,0.34,1,载波频率均为2 400 Hz。以16QAM信号数据集对网络进行训练,训练次数从1 000次到90 000次,损失函数变化曲线如图9所示。

图9 16QAM信号损失函数变化图

从图9中可以看到,训练初期,生成网络损失函数迅速下降,而判别网络损失函数迅速上升,表明初期生成网络的生成能力提升较快,逐渐学习到真实样本特征并生成样本骗过判别器。但判别器也在逐渐提升判别能力,两者进行对抗,在短暂的平稳状态之后,判别器的损失函数呈下降趋势,表明了判别器判别能力的提升。在对抗中,生成网络和判别网络都逐渐学习到了真实样本的特征,提升了各自的生成能力和判别能力,最终在训练40 000次后,两者损失函数趋于平稳,网络收敛。以16个码元为例,训练90 000次后所生成16QAM样本时域波形图和频谱图如图10所示。

图10 生成16QAM样本时域波形图和频谱图

图10(a)为生成16QAM样本的时域波形图,可以看到,每隔4个码元,波形的相位或者幅度产生一次变化,网络学习到了16QAM相位翻转和幅度变化的特征。图10(b)为生成16QAM样本的频谱图,与训练所用16QAM信号载波频率一致。

BPSK、QPSK和16QAM均只含有一个频率分量,而2FSK含有两个频率分量,运用载波信号的频率变化来携带信息,在时域上,两个频率分量的波形按码元信息的变化交替出现。实验所用2FSK信号采样频率为160 000 Hz,发送“1”时,载波频率为3 200 Hz,发送“0”时,载波频率为8 000 Hz,初始相位均为0。以2FSK信号数据集对网络进行训练时,损失函数变化曲线如图11所示,在训练40 000次之后,损失函数的变化趋势逐渐趋于平稳,网络迅速收敛。

图11 2FSK信号损失函数变化图

以10个码元为例,训练2 000次和90 000次后所生成样本时域波形图和频谱图如图12所示。

从图12中可以看到,在训练2 000次之后,生成网络已经能生成含有两个频率分量的干扰波形,生成样本频谱特征与训练所用2FSK信号的频谱特征一致,但此时在时域上两个频率的波形是均匀混在一起的,网络对2FSK信号的时域特征学习不够充分。在训练90 000次之后,网络逐渐学到了2FSK信号的时域特征,生成了两个频率波形不在同一时间出现的干扰波形。

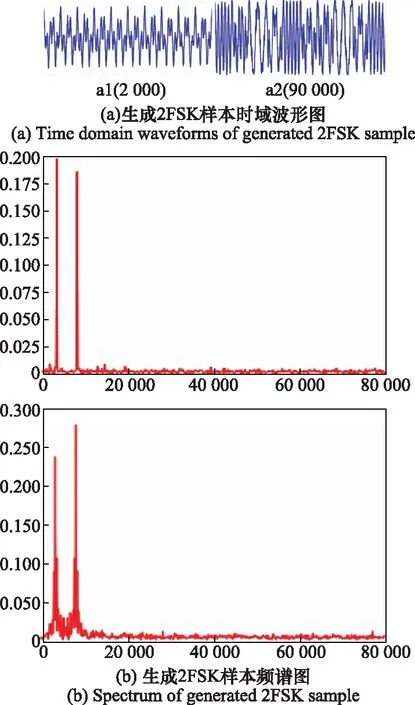
图12 生成2FSK样本时域波形图和频谱图

综上,可以看出本文GAN对其他类型和参数的目标信号也有较好的生成效果,能够生成与目标信号具有相似时域特性和频域特性的样本作为干扰波形,具有较好的应用泛化性。

2.3 实验3——干扰效果对比实验

通信干扰波形生成的最终目的是实现有效干扰,为说明本文干扰波形生成方法的有效性和较传统方法的优越性,将本文方法与最佳干扰、高斯噪声干扰进行了干扰效果对比试验。

在实验中,为充分观察干扰效果,以10 000个码元长度为例,分别以训练80 000次后所生成的干扰波形、最佳干扰波形和高斯噪声对目标通信系统进行干扰,在不同的干信比下各重复100次,取BER平均值,画干扰效果对比图。对BPSK、QPSK和2FSK通信系统来说,最佳干扰是与其具有相同调制方式、载波频率和码元速率的通信信号,因此在实验中,对随机生成的基带信号做不同的调制后作为BPSK、QPSK和2FSK通信系统最佳干扰波形。对16QAM通信系统来说,理论上最佳干扰是与其具有相同载波频率和码元速率的QPSK信号[21],但仿真中与目标信号具有相同载波频率和码元速率的16QAM信号进行干扰的效果与最佳干扰效果相差较小,并且低干信比时,以16QAM信号进行干扰的效果略优于QPSK信号,因此在本文实验中仍以与目标信号具有相同载波频率和码元速率的16QAM信号对16QAM通信系统的干扰效果作为最佳干扰。3种干扰对BPSK、QPSK、16QAM和2FSK通信系统的干扰效果对比如图13所示。

图13(a)为3种干扰下BPSK通信系统的BER,图13(b)为3种干扰下QPSK通信系统的BER,图13(c)为3种干扰下16QAM通信系统的BER,图13(a)为3种干扰下2FSK通信系统的BER。

图13 3种干扰下BPSK、QPSK、16QAM和2FSK通信系统的BER

从图13中可以看出,干信比相同时,生成干扰波形的BER比高斯噪声高很多,也即干扰效果比高斯噪声干扰明显得多。干信比较小时,与最佳干扰相比,生成干扰波形的干扰效果比最佳的干扰还要好,这也从一个侧面验证了所谓的最佳干扰波形也是在某一定的干信比范围内而言的;干信比较大时,生成干扰波形的BER低于最佳干扰的BER,但随着干信比的增加,生成波形BER曲线能够逐渐逼近最佳干扰的BER曲线。结合第2.2节中4种信号损失函数变化趋势和生成样本的仿真结果来看,在学习率取0.001时,运用4种信号的训练集训练网络,训练40 000次之后,网络的损失函数变化趋势都能逐渐变小,损失值趋于稳定,生成网络能够生成逼近真实样本分布的样本骗过判别网络,并且所生成干扰波形能对目标通信系统产生较好的干扰效果。

3 结 论

本文提出一种基于GAN的通信干扰波形生成技术,利用GAN能够自主学习训练集中数据的潜在分布并生成具有相同分布的样本的能力,将采集到的目标信号时域波形直接作为训练集对GAN进行训练,并将生成的与目标信号具有相似时域特性和频域特性的样本作为干扰波形,针对目标通信系统的信道实施干扰。与传统干扰方法相比,本文所提出的方法不需要关于目标信号特征的先验知识,能够自主提取目标信号的特征并生成干扰波形实施干扰,减少了人工决策的过程,解决了实际干扰过程中未知信号和参数动态变化的信号干扰的问题,在取得较好干扰效果的同时,也具有良好的应用泛化性。