多能源船舶电网风险评价指标体系构建方法
2021-04-07智鹏飞袁科琛
智鹏飞, 刘 芳, 杨 森, 袁科琛
(1.江苏科技大学 电子信息学院, 镇江 212100) (2.上海外高桥造船有限公司,上海 200137)
当今的海洋环境污染日益严重,航运业是污染的重要原因之一[1].目前,大部分船舶采用的发电机主要是柴油发电机,导致传统船舶电网不仅每年消耗大量石油,而且对环境造成严重影响.国际海事组织和世界各国正在积极采取各种有效措施,以减少船舶排放对大气的污染[2-3].由光伏电池、风力发电等可再生能源搭配蓄电储能装置,与传统柴油发电机组成的多能源船舶电网是现代船舶电网的主要发展方向之一[4-5].
目前关于多能源电网的研究主要集中在陆地新能源的可靠性分析和风险评估方面[6-7].在风力发电研究方面,文献[8]利用点估计来测量风电接入电网后有功功率的超限风险,搭建严重性模型和线路过载的概率模型用于衡量风险;文献[9-10]将风电和光伏输出预测误差与负荷预测误差的概率分布结合,估算线路有功功率超限风险和频率超限风险.在可靠性分析方面,文献[11]分析了变电站可靠性因素,以事件树形式描述开关处于各种操作状态的概率,结合条件概率获得可靠性指标;文献[12-13]将拉丁超立方采样应用于新能源电力系统的可靠性评估,重点关注可再生能源发电的间歇性和负载节点的波动性.文献[14-15]针对液化天然气(liquified natural gas,LNG)船的通航环境和泄露事故开展了定量风险评估方法研究.但是在多能源船舶电网方面,尤其是风险评估相关的研究成果很少,文中提出了风险评价指标体系建立原则,基于模糊动态层次分析法(fuzzy dynamic analytic hierarchy process,FDAHP)的指标权重计算方法,构建了多能源船舶电网风险评价指标体系,最后对功率波动下的多能源船舶电网进行了风险分析.
1 评价指标体系建立原则
多能源船舶电网是一个复杂而庞大的系统.因此必须按照“组件-单元-模块-系统”的次序完成系统风险评估.因此,多能源船舶电网风险评估指标体系的建立过程需要满足以下原则:
(1) 指标最简原则,指在能满足单元进行风险评估需求的情况下,应尽量保留较少的指标.即如果单元中的某个元件对单元的风险影响很小,在风险评估精度允许的情况下,为了提高评估速度,可以忽略该元件.
(2) 指标可测原则,指尽量选择容易定量计算的指标和容易准确确定的指标,尤其是尽量选择可以实验测试的定量指标,即被选作指标的元件的风险参数应该是容易定量计算或者是可以用实验测试数据分析得到的.
(3) 指标客观性原则,指被选作指标的元件能够真实的与被评估单元的风险发生联系,即被选作指标的所有元件的风险参数都必须与单元的风险参数有直接关系,较客观反映被评估单元在各种工况下的各项风险参数.
(4) 指标完备性原则,指被评估单元的综合风险评估指标体系的各个指标能较为全面地反映被评估单元的风险参数,即在满足最简原则的条件下,被评估单元中所有能够影响单元风险评估参数的元件,都要成为风险评价指标.
(5) 指标独立性原则,是指即风险评估指标体系中的各个指标都应尽可能地独立,减少指标内涵的重叠度,这样在确定指标权重时,可以在不考虑或少考虑指标重叠造成的影响的情况下得到较符合实际的权重.
以包含N个组件的单元为例,建立指标系统的过程如图1.
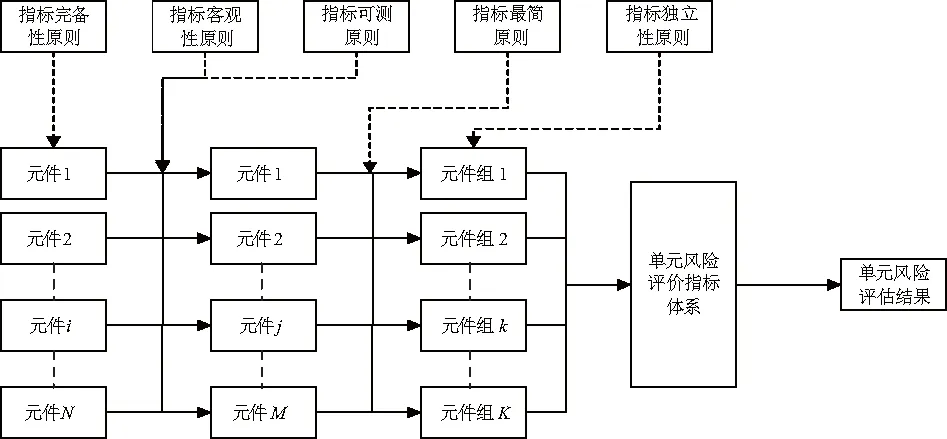
图1 单元风险评价指标体系建立过程图Fig.1 Process diagram of the establishment of unitrisk evaluation index system
如图1,对于包含N个元件的单元,首先要根据指标完备性原则即尽量将N个元件全部纳入风险评价指标体系;随后根据指标客观性原则和指标可测性原则,在保证指标完备性的基础上筛选出M个元件进行下一步风险评估;之后根据指标最简原则,将能作为元件组的元件整合成K个元件组或元件,这K个元件组或元件要保证指标独立性原则;最后建立单元风险评价指标体系对单元进行风险评估,并得到单元的风险评估参数.
2 FDAHP权重赋值方法
层次分析法(analytic hierarchy process,AHP)是将决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法.但是当某一层次评价指标很多时(4个以上),其思维一致性很难保证.在这种情况下,将模糊法与层次分析法的优势结合起来形成的模糊层次分析法(fuzzy analytic hietarchy process,FAHP),将能很好地解决这一问题[16].考虑到多能源船舶电网风险评估应该是个长期动态的过程,文中在FAHP的基础上引入动态层次结构,提出FDAHP来确定多能源船舶电网风险评估指标的权重,以保证指标权重的精确性、客观性和实时性.
2.1 层次评价结构
多能源船舶电网风险评估指标体系分为4层:第一层为预定目标(A),即多能源船舶电网风险评估这一目标;第二层为一级指标,包括多能源船舶电网的4种工况:启航(B1)、停车(B2)、倒车(B3)和突变负载(B4);第三层为二级指标,是一级指标下面的若干个子指标项,共16项,分别包括4种工况下发电模块、负载模块、输配电模块和推进模块的风险指标;第四层为三级指标,是二级指标下面的光伏发电模块、风力发电模块等若干个子指标项,共44项;第五层为四级指标,是三级指标下面的光照强度、风速等若干个子指标项,共132项.
2.2 构建FAHP比较判断矩阵
根据AHP常用的九级标度法,结合三角模糊集合构建方式,定义成对比较的九级标度模糊判断术语来搜集专家意见如表1.
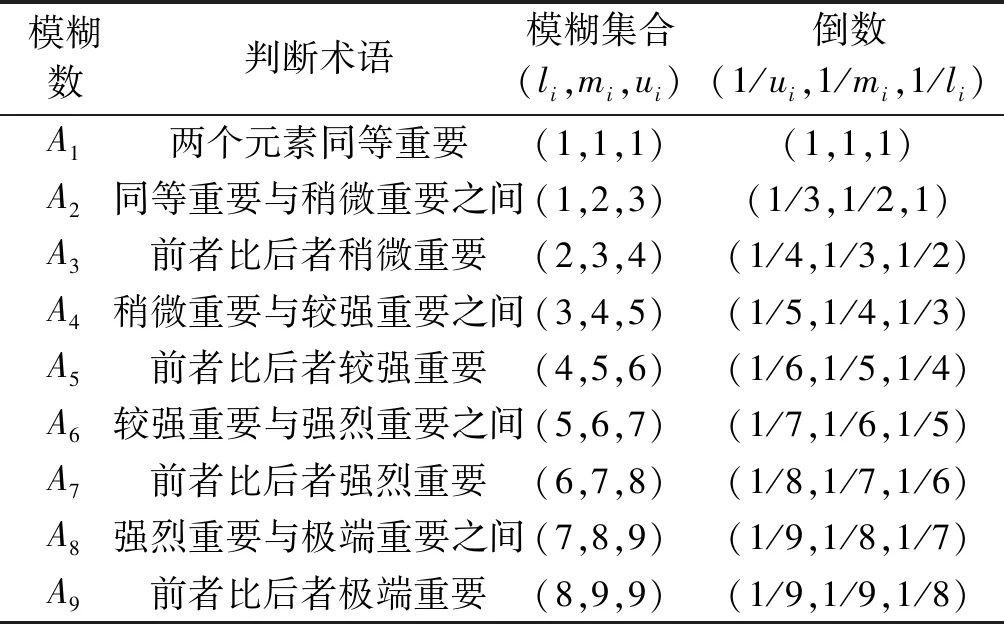
表1 判断术语的模糊集合Table 1 Determine the fuzzy set of terms
根据表1所述的模糊判断术语,搜集每个专家的判断意见,对各层级指标构建模糊判断矩阵,假设层次模型中某层级具有j个因素,用aij表示第i个因素对于第j个因素的重要性比较结果,该层级的判断矩阵A为:
A=(aij)n×m=
i,j=1,2,…,n;i
(1)
2.3 权向量概率分布计算
通过对FAHP权向量的概率分布计算,得到同一层指标的模糊权重,具体计算过程如下.
首先计算FAHP判断矩阵A的列向量之和:
i=1,2,…,n
(2)
式中:RSi为第i列向量之和.对FAHP判断矩阵A进行归一化计算得到权向量三角模糊数为:
i=1,2,…,n
(3)
式中:Si为判断矩阵A第i个指标权重的三角模糊数,(S1,S2,…,Sn)T组成FAHP判断矩阵A的特征向量.
对模糊动态判断矩阵权重向量进行计算,第i个因素满足n个目标的综合程度值计算公式为:
Si(t)>=(sui(t),smi(t),sli(t))=

(4)
第i个因素的未归一化权重为:
(5)
式中:α∈[0,1]为判断系数,α=1时,表示决策者完全认同;α=0时,表示决策者完全否决;0<α<1表示决策者的认同度介于认同和否决之间.
之后确定专家动态权重,设n个专家给出的判断矩阵在时间t所得归一化权向量分别为w1(t),w2(t),……,wn(t),时间t的历史数据为w(t).则在时间t,wi(t)与w(t)的相似度为:
φi(t)=cosθi(t)=
(wi(t)·w(t))/(|wi(t)|·|w(t)|)
(6)
定义时间t向量wi(t)与w(t)的偏差度为:
Di(t)=1-φi(t)i=1,2,…,n
(7)
若Di(t)≠0(i=1,2,…,n),令第i位专家的权向量为:
(8)
若Dik(t)=0(k=1,2,…,n),令βik(t)=1/k,其余Dik(t)≠0的专家的权都为零.
然后确定动态层次结构模型,根据时间t历史数据和专家给出的判断矩阵得出的权向量定出每个专家的权值,之后计算出t+Δt时间的每个因素的最终权向量:
w(t+Δt)=
(9)
3 风险评价指标体系构建
根据风险评价指标体系建立原则,构建多能源船舶电网风险评价指标模型,如图2.
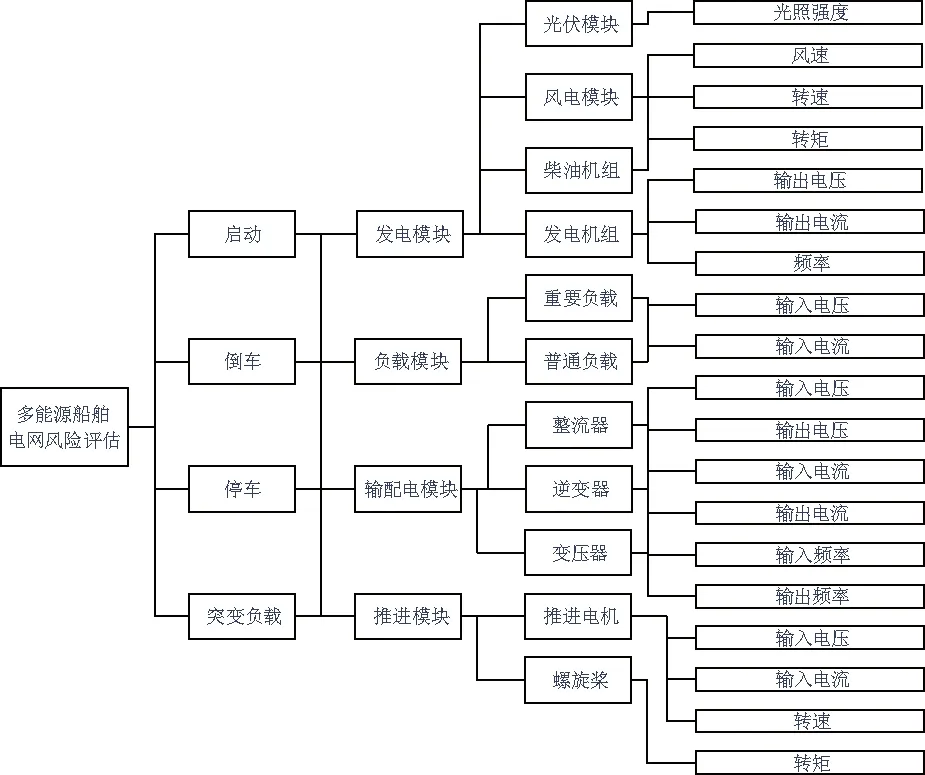
图2 多能源船舶电网风险评价指标体系模型Fig.2 Multi-energy ship power grid riskevaluation index system model
如图2,整个系统风险评估模型包括启航、倒车、停车和负载突变4种工况作为一级指标.在每种工况下,发电模块,负载模块,输配电模块和推进模块的风险因素作为二级指标.四大模块的每个子系统或设备的风险因素作为第三级指标,各子系统和设备所包含的单元风险作为四级指标.
聘请20名与多能源船舶电网相关的高校和研究机构的专家对判断矩阵A中的指标进行评分,基于专家评分结果进行综合分析和统计,评价多能源船舶电网风险评价体系中各级评价指标的重要性,构建初始FAHP判断矩阵(表2).
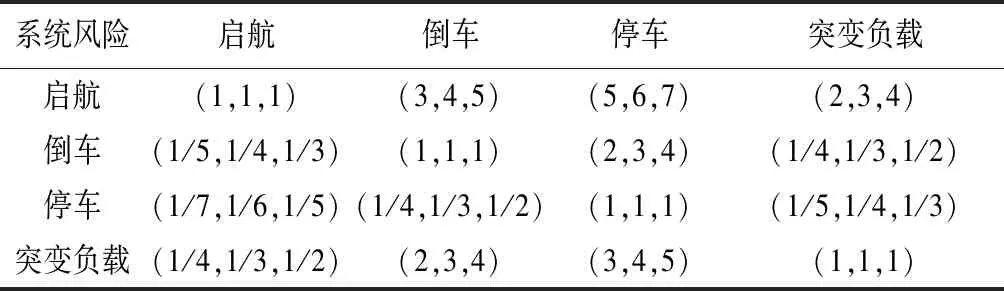
表2 一级指标初始FAHP判断矩阵Table 2 Initial FAHP judgment matrixof first-level indicators
根据专家对于各层级指标的两两比较判断意见组成的各层级FAHP判断矩阵,得到各层级FDAHP权向量,以一级指标初始FAHP判断矩阵为例,计算其权向量为:
(10)
在初始FAHP矩阵的基础上可得到各层级指标的整体排序,采用FDAHP方法进行指标体系的整体权重赋值.表3是多能源船舶电网风险评价指标体系的权重赋值结果,也是所构建的最终评估指标体系,由于篇幅关系,仅以一级指标启航下的评价指标体系为例.

表3 多能源船舶电网风险评价指标体系权重赋值结果Table 3 Weight assignment resultsof multi-energy ship power grid risk evaluation index system
4 多能源船舶电网实验与仿真分析
4.1 多能源船舶电网半物理仿真实验
实验数据来自于半实物仿真平台,包括光伏发电设备、风力发电设备、柴油发电机、蓄电池、普通负载、突变负载、推进电机、螺旋桨负载、智能配电柜、中央控制台、RT-LAB仿真器等(图3).

图3 多能源船舶电网半实物仿真平台Fig.3 Multi-energy ship power grid semi-physicalsimulation platform
依托半实物仿真平台,通过前期实验发现,多能源船舶电网的稳定性与光照强度和风力大小有一定的联系.通过在4种不同光强和风力工况下分别进行100次负载多次突变工况下的半物理仿真实验(每次持续1 h),得到系统故障次数和平均无故障运行时间数据如表4.

表4 负载突变下系统实验数据Table 4 Experimental data graph undersudden load conditions
4.2 多能源船舶电网风险评价仿真分析
多能源船舶电网风险评价主要由两个系统风险参数表示:风险发生概率(PRO)和期望缺供电力(EDNS,MW),
(1)系统风险发生概率
风险发生概率是多能源船舶电网工作时故障发生的概率.在多能源船舶电网中,假设系统节点总数为NU,则节点k的风险发生概率为:
(11)
式中:Pik为与单元节点k处于失效停运状态i的概率;Nk为引起单元节点k削减单元的状态总数.
则系统风险发生概率PRO为:
(12)
(2)系统期望缺供电力
系统期望缺供电力是当船舶综合电力推进系统发生风险时,所损失的负载功率的期望值,假设系统的单元节点数为NU,则单元节点k的期望缺供电力EDNSk为:
(13)
式中:Lk为单元节点k的平均单元功率,MW.则系统期望缺供电力EDNS为:
(14)
选取强风有光照和弱风无光照两种工况,以某实际多能源船舶电网为例(光伏和风力发电容量约占全船电网发电容量的50%),按船舶电网实际参数搭建模型进行仿真.风险发生概率PRO和期望缺供电力EDNS曲线分别如图4,5.
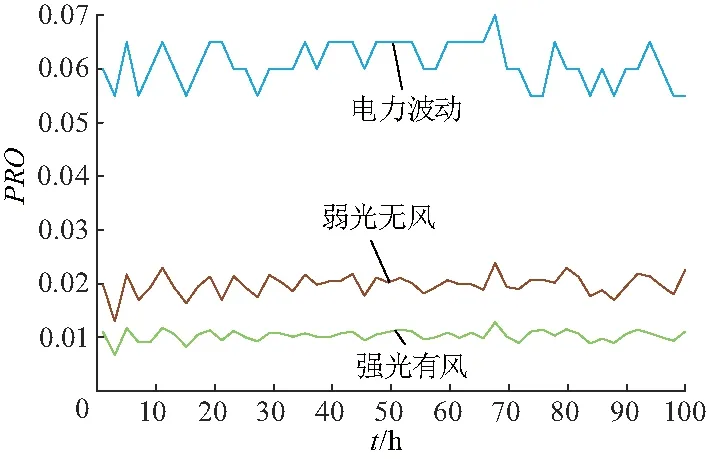
图4 两种工况下系统风险发生概率PRO曲线Fig.4 >PRO curve under two working conditions
在图4和图5中,多能源船舶电网的系统风险发生概率PRO随着功率需求的波动而变化,并且在弱光和无风的条件下系统的PRO和EDNS高于强光和大风条件下的PRO和EDNS.结果与多能源船舶电网的半实物仿真平台实验情况一致,验证了文中方法的正确性.

图5 两种工况下系统期望缺供电力EDNS曲线Fig.5 >EDNS curve under two operating conditions
5 结论
(1) 提出一种基于FDAHP的多能源船舶电网风险评价指标体系构建方法,建立了多能源船舶电网风险评价模型,并在强风有光照和弱风无光照两种工况下进行了仿真.
(2) 仿真结果表明,光伏和风电模块可以提高船舶微电网在需求功率发生波动时的系统鲁棒性,降低风险发生概率和系统期望缺供电力,该结果与多能源船舶电网的半实物仿真平台实验情况一致.验证了文中提出方法的正确性.该方法也可适用于其他微电网和电力系统,应用前景广泛.
参考文献(References)
[1] HUANG A Q, CROW M L, HEYDT G T, et al. The future renewable electric energy delivery and management (FREEDM) system: the energy internet[J]. Proceedings of the IEEE, 2010, 99(1): 133-148. DOI:10.1109/JPROC. 2010. 2081330.
[2] KRAUSE T, ANDERSSON G, FROHLICH K, et al.Multiple-energy carriers: modeling of production, delivery, and consumption[J]. Proceedings of the IEEE, 2010, 99(1): 15-27. DOI:10.1109/JPROC.2010.2083610.
[3] ABE R, TAOKA H, MCQUILKIN D. Digital grid: Communicative electrical grids of the future[J]. IEEE Transactions on Smart Grid, 2011, 2(2): 399-410.DOI: 10.1109/TSG.2011.2132744.
[4] LASSETER R, AKHIL A, MARNAY C, et al. The CERTS microgrid concept[R]. White paper for Transmission Reliability Program, Office of Power Technologies, US Department of Energy, 2002, 2(3): 30.
[5] BOYD J. An internet-inspired electricity grid[J]. IEEE Spectrum, 2012, 50(1): 12-14. DOI: 10.1109/MSPEC. 2013. 6395291.
[6] XUE Yusheng. Energy internet or comprehensive energy network?[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(3): 297-301. DOI:10.1007/s40565-015-0111-5.
[7] NAZAR M S, HAGHIFAM M R. Multiobjective electric distribution system expansion planning using hybrid energy hub concept[J]. Electric Power Systems Research, 2009, 79(6): 899-911.DOI:10.1016/j.epsr.2008.12.002.
[8] LI Xue, ZHANG Xiong, WU Lei, et al. Transmission line overload risk assessment for power systems with wind and load-power generation correlation[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1233-1242. DOI:10.1109/TSG.2014.2387281.
[9] NEGNEVITSKY M, NGUYEN D H, PIEKUTOWSKI M. Risk assessment for power system operation planning with high wind power penetration[J]. IEEE Transactions on Power Systems, 2014, 30(3): 1359-1368. DOI: 10.1109/TPWRS. 2014.2339358.
[10] CUI Mingjian, ZHANG Jie, HODGE Bri-Mathias, et al. A methodology for quantifying reliability benefits from improved solar power forecasting in multi-timescale power system operations[J]. IEEE Transactions on Smart Grid, 2018,9(6): 6897-6908. DOI: 10.1109/TSG.2017.2728480.
[11] MATOS M A, BESSA R J. Setting the operating reserve using probabilistic wind power forecasts[J]. IEEE Transactions on Power Systems, 2010, 26(2): 594-603. DOI: 10.1109/TPWRS.2010.2065818.
[12] HAJIAN-HOSEINABADI H. Impacts of automated control systems on substation reliability[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 1681-1691. DOI: 10.1109/TPWRD.2011.2119404.
[13] SHU Z, JIRUTITIJAROEN P. Latin hypercube sampling techniques for power systems reliability analysis with renewable energy sources[J]. IEEE Transactions on Power Systems, 2011, 26(4): 2066-2073. DOI: 10.1109/TPWRS. 2011.2113380.
[14] 张仕元,刘德新,朱景林,等.基于云模型的LNG船舶通航环境风险评价[J].江苏科技大学学报(自然科学版),2018,32(3):325-331.DOI: 10.11917/j.issn.1673-4807.2018.03.003.
ZHANG Shiyuan, LIU Dexin, ZHU Jinglin, et al. Risk evaluation for the navigation environment of the LNG ship based on the cloud model [J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2018,32(3):325-331. DOI: 10.11917/j.issn.1673-4807.2018.03.003.(in Chinese)
[15] 王庆丰,崔相义.内河水域LNG运输船泄漏事故的定量风险评估[J].江苏科技大学学报(自然科学版),2019,33(1):16-20.DOI:10.11917/j.issn.1673-4807.2019.01.003.
WANG Qingfeng, CUI Xiangyi. Quantitative risk assessment on leakage accidents of LNG carriers in inland rivers [J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2019,33(1):16-20.DOI: 10.11917/j.issn.1673-4807.2019.01.003.(in Chinese)
