基于模糊PID控制的船用胎架高度联控方法研究

刘金锋， 王 镇， 景旭文*， 唐明明， 曹旭武， 董建伟， 赵晨华

(1.江苏科技大学 机械工程学院， 镇江212100) (2.陕西柴油机重工有限公司， 兴平 713100)

船体分段是通过连接板构件的对接焊以及与加筋板的角接焊制造而成的，部件和分段的焊接变形会给船体下一阶段的焊接和装配带来较大的困难，同时还会引起舱壁和外板的凹凸变形，使得船体结构强度降低.目前对船舶的变形与监测问题研究较多,包括船舶薄板结构焊接变形[1]、船舶驾驶室变形[2]、船舶板材和加强筋的焊接变形[3]、船舶甲板变形监测[4]、船体变形量检测[5]等方面.

但对于船舶建造过程中变形研究主要集中在焊前阶段，装焊过程中的变形矫正研究较少.在分段装焊过程中，通过胎架高度的调整，给予分段变形补偿，达到在焊中和焊后控制焊接变形的目的.文献[6]基于工控机、运动控制器和PLC的设计了水火弯板数字胎架控制系统，文献[7]提出的新型通用胎架，实现了胎架高度的无级调节.文献[8]提出一种基于现场采集数据的高度计算方法，提高了胎架定位高度的准确性.文献[9]将柔性胎架系统和造船精度控制技术结合，实现胎架高度调节的自动化.文献[10]集合现有各类胎架形式的特点，提出一种数控调形胎架，可调整支撑杆的高度.文献[11]设计一种集光机电控于一体的数控胎架系统，根据需要调整的高度对胎架进行调整，存在不能自适应调整的问题，导致胎架不能较好控制分段焊接变形，且各个胎架相互独立，高度调整时需要依次调节，导致建造效率较低.

但目前对胎架高度调控方面的研究不够深入，而模糊PID算法正好可以弥补上述缺点，且应用较广泛.文献[12]基于模糊神经网络研究了船用螺旋桨高阶曲面打磨问题.文献[13]基于模糊PID控制研究了三连杆平面刚性机器人机械手的控制问题.文献[14]基于正交模糊PID控制设计串联机械手驱动系统.文献[15]利用模糊PID控制器对集成电力系统进行有效的控制.

针对上述问题，文中研究船舶分段建造过程中胎架高度调控的问题.首先，基于船舶分段拟合曲面模型建立胎架理论高度补偿模型；其次，提出不同关联关系类型下胎架位置、数量及阶层数的判定方法，建立胎架间的动态响应策略，实现胎架间的联合调控；然后，基于模糊PID控制算法，实现胎架系统高度联合调控；最后，利用智能胎架系统进行验证分析，并与传统PID算法对比分析，结果表明文中方法具有较高的稳定性.

1 基于船舶分段拟合曲面的胎架高度补偿模型创建

目前胎架高度值的计算主要通过经验法或船舶型值表获得，导致胎架高度调整精度较差，为此，本文提出一种基于船舶分段拟合曲面的船用胎架高度模型创建方法，实现在焊中阶段胎架高度补偿，达到控制分段变形的目的.

分段外板曲面拟合方法包括：多项式插值法、参数样条曲线曲面、Bezier方法、B样条、非均匀B样条曲线(NURBS)等[16],由于非均匀B样条曲线能够为解析曲线曲面的表达提供一种统一的数学方法，其算法执行速度快、数值稳定，非均匀B样条曲线被广泛应用到船体分段外板的曲面拟合过程中.

首先，获取分段外板的离散点，根据离散点反算3次曲面控制点；然后，基于控制点计算拟合方程.其中拟合曲面基础数学模型为：

(1)

式中：0≤u,v≤1，取k=3，即三次NURBS曲面;u,v为形式化参数；m,n分别为在u和v方向上的控制点的个数；Vε,j(ε=0,1,…,m;j=0,1,…,n)为控制网格顶点；Nε,k(u),Nj,k(v)为非有理B样条基函数.

设胎架平面位置坐标为(Xϑ，Yϑ)，在求取坐标S(u,v)时，需对坐标进行参数化变换, 故S(u,v)变换为：

(2)

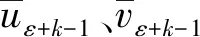
设活络头的最低倾斜角为θ，活络头的厚度为L,胎架支撑点位坐标(Xl,Yl,Zl)为：

(Xl,Yl,Zl)=(Xϑ,Yϑ,S-Lcosθ)

(3)

则胎架高度补偿模型表示为：

(4)

2 胎架系统关联关系的建立

2.1 胎架间关联关系类型的创建

胎架分布模型如图1，基于分段变形范围和载荷情况，文中将胎架间的关联关系分为串行连接和环行连接.其中，将在分段变形和载荷范围内布置于同一轨道时胎架的关联关系称为串行连接，如图2(a)；将在分段变形和载荷范围内布置于不同轨道时胎架的关联关系称为并行连接，根据胎架的不同位置排列方式，并行连接包括星形连接和环形连接，如图2(b)、(c).

图1 胎架分布模型Fig.1 Distribution model of mould bed

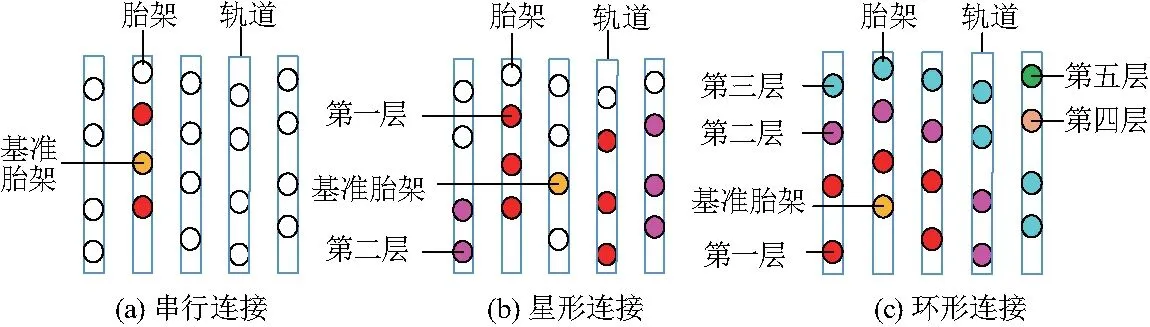
图2 关联类型分类Fig.2 Type of incidence relation

同时做出如下定义：

定义1基准胎架：为中心胎架，其为分段变形时载荷较大处或距离载荷较大处最近的胎架；

定义2从属胎架：为各阶层上的胎架，其在动态响应方法的作用下，实现与基准胎架的动态响应；

定义3阶层：为星形连接和环形连接的层数目.

并行连接以基准胎架为中心，由内向外依次划分为不同的阶层，阶层的数量以及各阶层上胎架数量及其位置需要根据具体情况确定.其中，星形连接以基准胎架为中心，由内向外相互对称的两个轨道上的胎架为同一阶层，环形连接以基准胎架为中心，各阶层由内向外依次环绕于基准胎架周围.

2.2 胎架间关联关系类型确定方法

当为串行连接时，由于基准胎架和从属胎架位于同一轨道上，因此其阶层数目为1层，从属胎架数量基于分段变形范围和本轨道上的胎架数目即可确定.

当为并行连接时，高度补偿中各阶层胎架数量及其位置确定方法如图3.其中，为星形连接时，根据各阶层中胎架的原始胎架数量和变形区域，确定在变形区域内，各阶层中不同轨道上的胎架数量，然后，基于两点间距离公式确定其中与基准胎架距离最短的胎架数量；为环形连接时，判断各阶层在同一轨道上是否存在多个胎架，若存在，则基于同一阶层中不同轨道上的相邻胎架夹角最大的原则剔除多余胎架，然后，将本阶层剔除的胎架归入下一阶层，重复上述过程，可得各阶层的胎架数量及其位置.

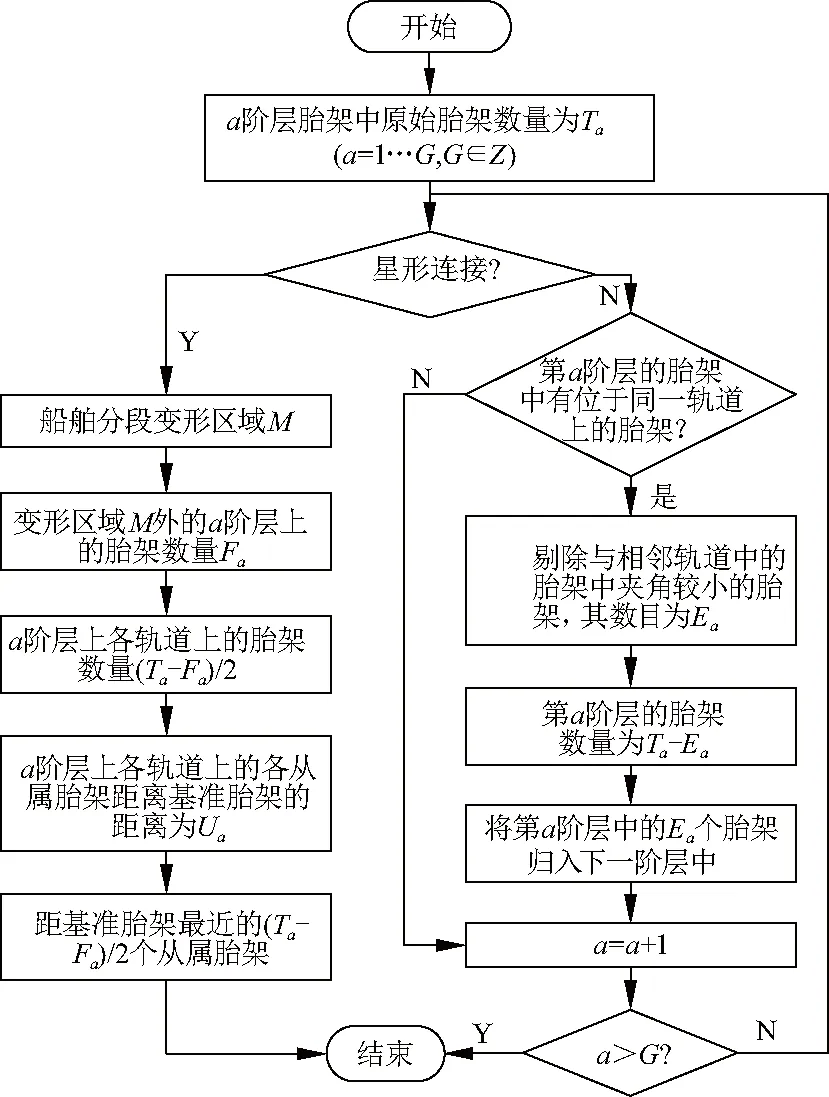
图3 各阶层胎架数量及位置确定方法Fig.3 Determination method of quantity and locationfor mould bed in each layer

高度补偿的阶层数目确定方法如图4.首先，初步确定变形区域内的层数；其次，根据反变形力确定变形区域内的基准胎架及其压力；然后，以基准胎架为中心，依次计算各层胎架的总压力.

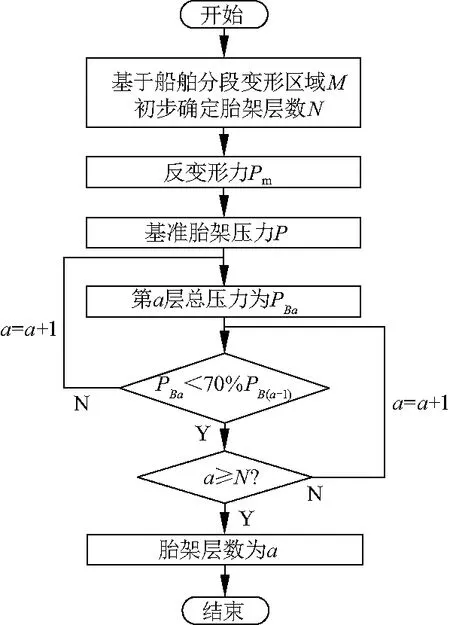
图4 高度补偿阶层数确定方法Fig.4 Determination method for numberof height compensation

经计算，当本阶层胎架压力之和PBa小于上一层胎架压力之和为70%，即PBa<70%PB(a-1)时，本阶层胎架的压力可由上一阶层胎架进行分担，因此需要同时保证临界层的胎架压力之和大于等于上一阶层胎架压力和的70%.最后；在压力符合的条件下，比较此时胎架阶层数和初步确定的胎架层数间的关系最终确定胎架的阶层数.

3 模糊PID控制算法设计

为达到船舶曲面分段变形补偿的目的，文中提出一种基于模糊PID控制算法的船用胎架高度联控方法，包括模糊控制和PID控制两部分，其中硬件包括步进电机、步进电机驱动器、Zigbee模块等，其控制原理如图5，经过PID控制实现胎架系统的自适应控制.

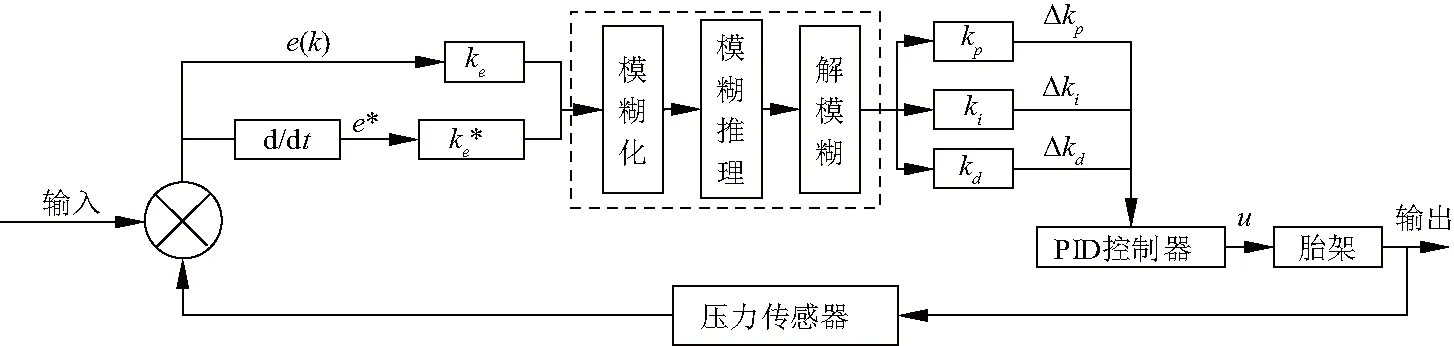
图5 模糊PID控制原理Fig.5 Control principle of fuzzy PID

3.1 精确变量模糊化

输入量为胎架实际受压载荷P和理论载荷P0之误差e以及误差变化率e*，输出量为胎架的高度H，则模糊控制器为双输入-单输出的基本模糊控制器.

设误差e的基本论域为[-30%,30%],输入语言变量E的论域为：

X=[-6 -5 -4 -3 -2 -10 +1 +2 +

3 +4 +5 +6]

(5)

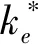
(6)

语言变量E选取7个语言值:

{NB NM NS ZO PS PM PB}(分别表示负大、负中、负小、零、正小、正中、正大)

根据建造经验，模糊变量的隶属度函数取为高斯型.

3.2 模糊控制规则的建立

根据控制策略，可得出一组由49条模糊条件语句构成的控制规则，其形式为“if e ande*then U”的模糊控制语句，根据该模糊控制语句可得到相应的模糊关系Ri，则船舶曲面变形补偿控制规则的总模糊关系为：

(7)

自适应模糊整定的PID数学模型为：

{ΔkpΔkiΔkd}=e(k)(ke+kei(e(k)-e(k-1))f(e,ec))

(8)

离散PID控制算法为：

(9)

其中：ΔkpΔkiΔkd是模糊集合kp,ki,kd的比例因子的变化值;e(k)为系统偏差;u(k)为系统最终的输出控制量;的比例因子是通过模糊PID调节之后的值.

最终得到kp,ki,kd比例因子的模糊控制规则如表1.

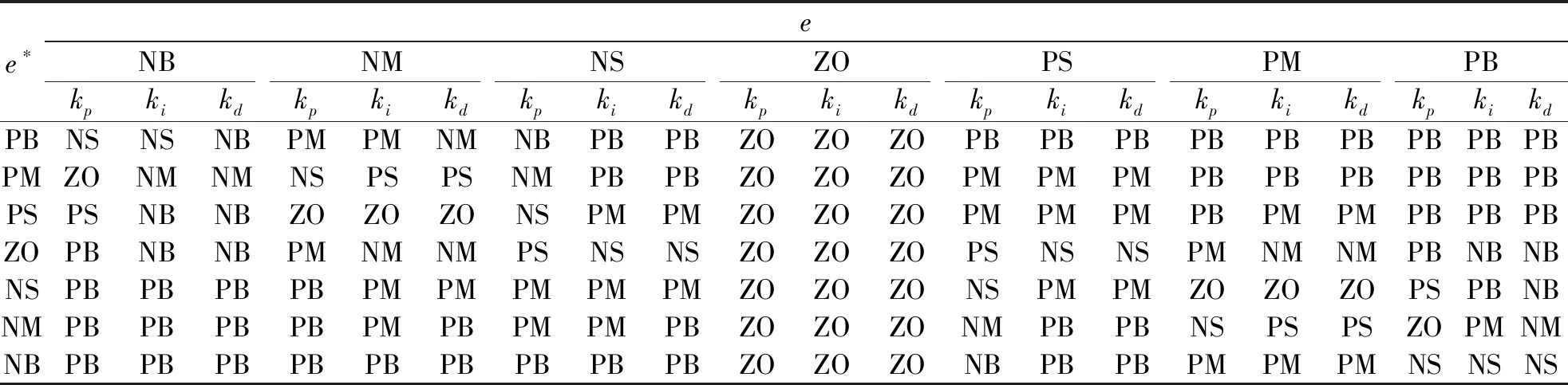
表1 kp,ki,kd模糊控制规则Table 1 Fuzzy control rule of kp,ki,kd

3.3 模糊推理及反模糊化

根据相关去模糊化方法的特点，文中选择加权平均法，其函数为：

(10)

其中：yi为第模糊控制量论域内第i个单点模糊值；u(yi)为yi对应的隶属度；y*为模糊控制器输出量解模糊后的精确值.

yi对应的隶属度u(yi)计算方法为：

u(yi)=uNB(e)ΔuNB(e*)=min{uNB(e),uNB(e*)}

(11)

由此，可计算出kp,ki,kd在不同偏差e和偏差变化率e*下的参数值，如表2，由表2可得kp,ki,kd的语言变量赋值(表3).

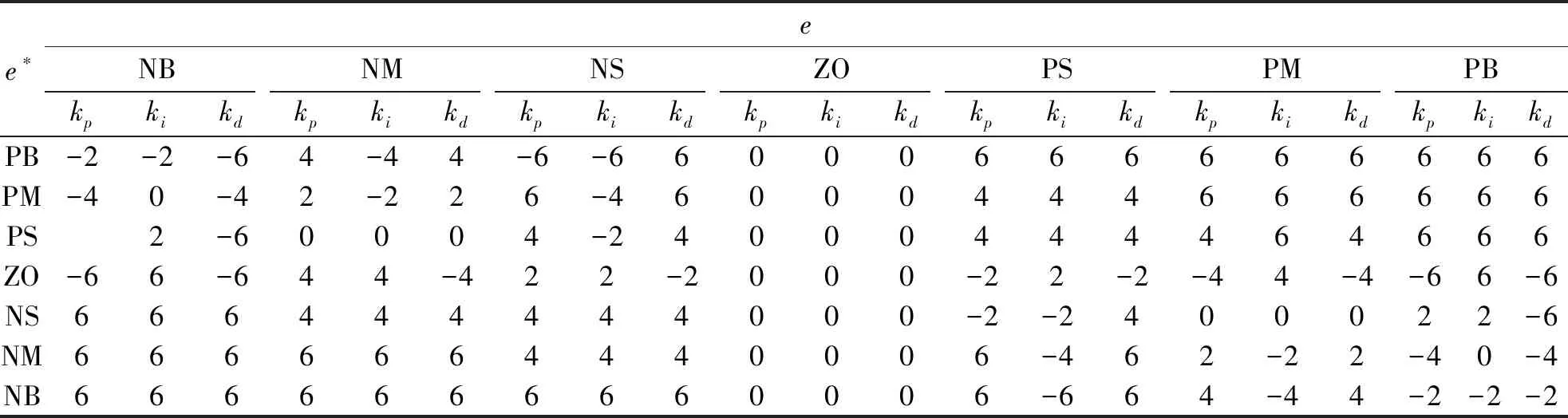
表2 kp在不同e和e*下的参数表Table 2 Parameter list of kp,ki,kd in e and e*

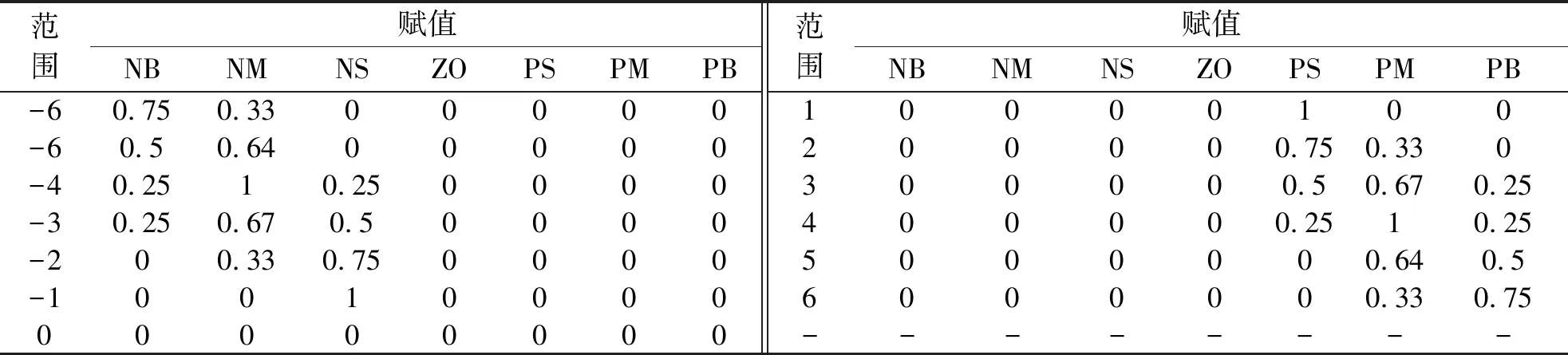
表3 kp,ki,kd的语言变量赋值表Table 3 Assignment table of linguistic variable for kp,ki,kd

基于船舶分段拟合曲面的胎架高度补偿模型计算基准胎架理论高度Zl，模糊PID算法用于各从属胎架的高度调控.首先，基于船舶分段拟合曲面的胎架高度补偿模型创建方法实现基准胎架调整至理论高度Zl；然后，基于胎架间关联关系确定基准胎架和从属胎架的关联类型、阶层数a以及各阶层上的胎架数量和位置，实现基准胎架和从属胎架间的联通；最后，在模糊PID控制算法的作用下，各从属胎架基于实际受压载荷P和理论载荷P之误差e以及误差变化率e*，输出从属胎架的高度H，实现从属胎架高度基于基准胎架高度的自适应调整，从而实现胎架模型数据和模糊PID算法数据的关联，最终实现胎架系统高度联合调控.

4 实验

为验证文中方法，搭建了模拟分段建造过程，其中包括船舶曲面分段、智能胎架以及移动轨道.船舶曲面分段建造现场胎架布置示意如图6，已知分段宽度为1 964 mm，长度为2 625 mm，轨道间距为80 mm,船体分段总质量为18 t，每个胎架的支撑质量不超过3 t，胎架数量为6个.

图6 面向船舶分段建造现场的胎架布置示意Fig.6 Mould bed distribution in ship building

4.1 模糊PID控制算法的仿真分析

在MATLAB/Simulink中对模糊PID控制算法进行仿真.模糊控制规则(共49条模糊控制规则)如图7.

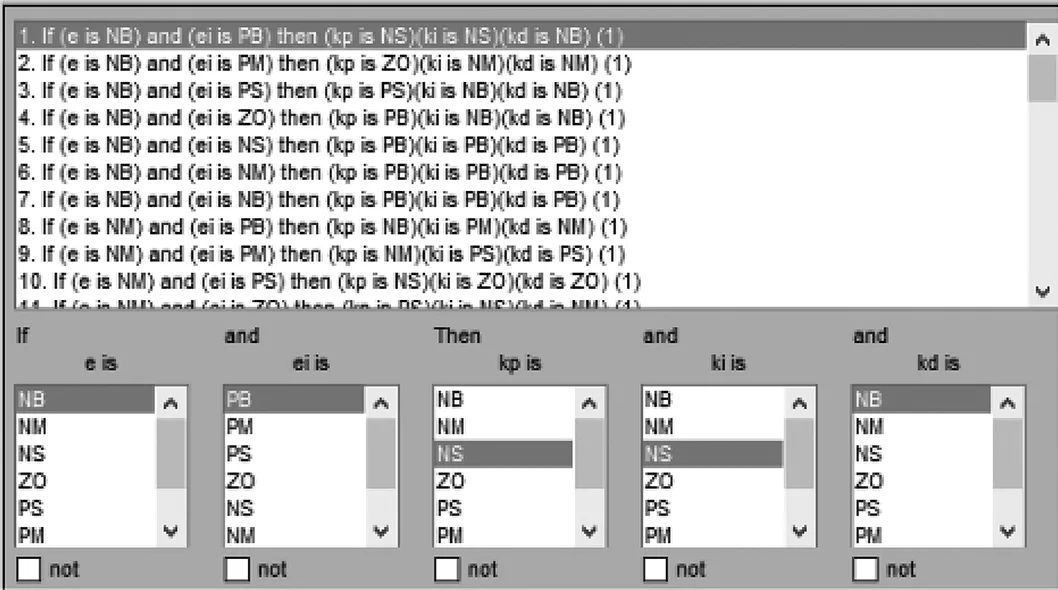
图7 模糊控制规则Fig.7 Fuzzy Control Rules

基于设计的控制器和控制规则，生成的kp,ki,kd表面预览界面如图8.kp,ki,kd凹凸不平的的曲面表明该控制规则具有较好的控制效果.

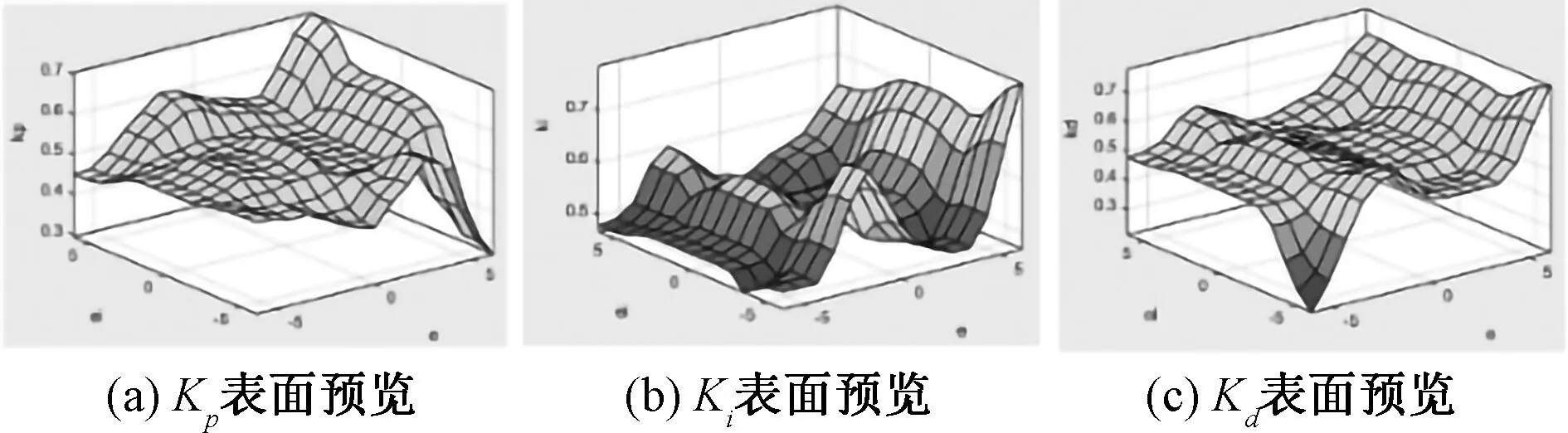
图8 kp,ki,kd拟合曲面Fig.8 Surface preview of kp,ki,kd

如图9，对模糊PID与常规PID进行建模.两者对比如图10，传统PID响应时间为16.893 s,而模糊PID响应时间约为7.315 s，响应时间明显缩短，且模糊PID控制的幅值变化相比传统PID控制变化较小，动态特性显著提升.

图9 仿真模型Fig.9 Simulation model

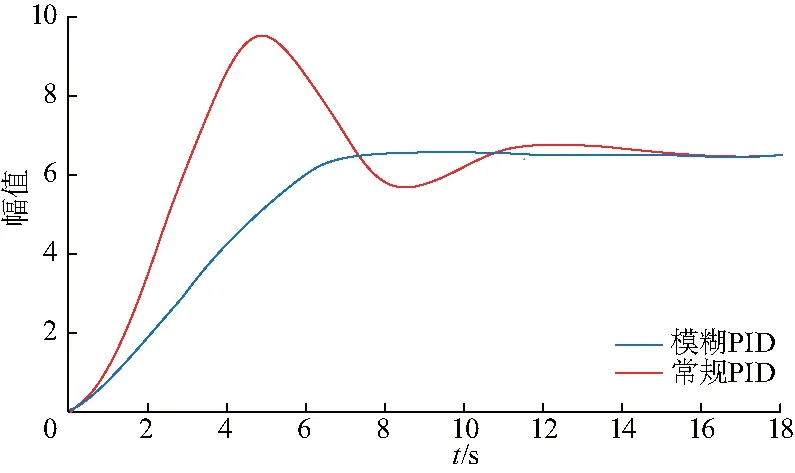
图10 模糊PID和常规PID的控制结果Fig.10 Results of Fuzzy PID and conventional PID

4.2 智能胎架系统补偿高度计算及其关联关系验证分析

智能胎架系统如图6，系统中活络头厚度为28 mm,丝杠初始定位高度为240 mm,已知船体部分型值表如表4.

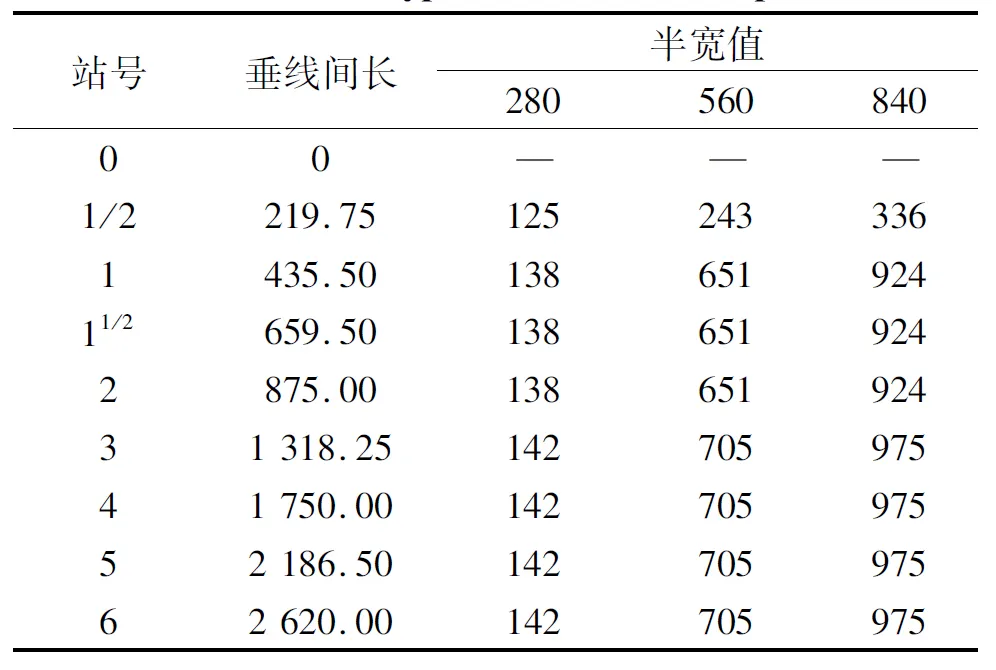
表4 船体分段型值表Table 4 Type value table of ship mm

在型值表中取型值点并转换坐标系后的坐标值如表5，基于上述数据计算各个胎架与分段外板接触点的坐标如表6.

表5 船体分段外板坐标值Table 5 Coordinates of ship block

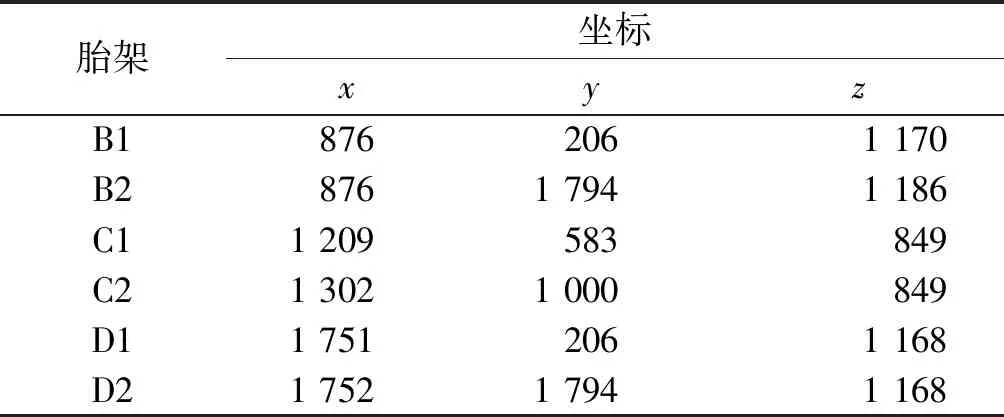
表6 胎架与分段外板接触点坐标Table 6 Contact point coordinates of mould bed with ship block

由表6进行坐标变换后，求得B1、B2、C1、C2 、D1、D2胎架理论支撑高度分别为{560,560,240,240,562,562}.

根据各个胎架的位置排布关系确定胎架系统的关联关系，当胎架系统处于稳定状态时，各个胎架承受压力的合理范围是9 891 N≤P≤18 712 N，当18t的船舶分段放置在胎架系统上时，其变形区域M位于C1胎架附近,且经压力传感器监测，C1胎架此时的压力为23 451.3 N, 变形区域M的最大半径为463.7 mm.

如图11，文中以C1胎架作为基准胎架建立关联关系，根据此胎架系统的排布方式，其关联关系类型为环形连接，经检测确定变形区域M的最大半径为703 mm，C1距离B1、B2、C2、D1、D2分别为503、1 255、417、661、1 327 mm，由变形补偿层数确定方法，首先，初步确定胎架阶层数为2层，且第1层胎架为C2,第2层胎架为B1、D1；其次，根据建造经验，此时所需的反变形力Pm=2 348.1 N，第1层即C2此时的压力为19 637 N,第2层中B1胎架的压力为6 834 N,D1胎架的压力为6 812 N，P2<70%，所以此时的层数为2层.

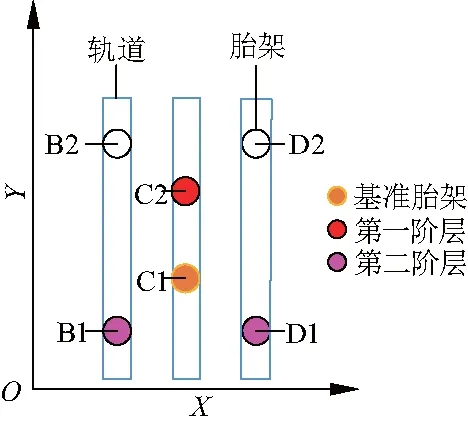
图11 胎架间关联关系Fig.11 Relationships among mould bed

根据各阶层胎架数量确定方法，此时胎架系统为环形连接，且各阶层无位于同一轨道上的胎架，所以第1阶层胎架数量为1个，第2阶层胎架数量为2个.

5 结论

(1) 基于船舶分段拟合曲面建立胎架高度补偿模型，基于分段变形区域和反变形力等约束条件定义各胎架间的关联关系，并建立胎架系统间的动态响应策略.

(2) 基于模糊PID控制算法研究船用胎架高度联控方法，可实现胎架系统的联合调控和自适应控制，达到控制船舶曲面分段变形的目的.运用模糊PID算法对船用胎架系统进行高度联控，通过Simulink模块仿真，结果表明其具有较好的稳定性和较快的动态响应特性.

(3) 所提出的控制方法在结合其他船舶设计特点及相关算法进行优化设计后，可适用于船舶动力定位系统控制、电力系统稳定性控制、船用柴油机调速系统控制以及舵机控制系统设计等方面.

参考文献(References)

[1] 袁红莉,闫永思.基于热弹塑性有限元法船舶薄板结构焊接变形模拟与预报[J].舰船科学技术,2018,40(9):52-55. DOI：10.3404/j.issn.1672-7649.2018.05.009.

YUAN Hongli, YAN Yongsi.The numerical simulation and prediction of welding deformations under different welding sequences based on thermal elastic-plastic finite element method[J].Ship Science and Technology,2018,40(9):52-55.DOI：10.3404/j.issn.1672-7649.2018.05.009 (in Chinese)

[2] 刘小尧,刘滨.防止船舶驾驶室变形的方法研究[J].广东造船,2018,37(6):40-42.

LIU Xiaoyao, LIU Bin.Anti-deformation method for wheelhouse[J].Guangdong Shipbuilding,2018,37(6):40-42.(in Chinese)

[3] KIM M，KANG I，CHUNG H. Simplified welding distortion analysis for fillet welding using composite shell elements[J].International Journal of Naval Architecture & Ocean Engineering, 2015,7(3):452-465.DOI:10.1515/ijnaoe-2015-0032.

[4] 王秀艳.基于SVD矩阵算法的船舶甲板变形监测研究[J].舰船科学技术,2018,40(7A):19-21.DOI:10.3404/j.issn.1672-7649.2018.7A.007.

WANG Xiuyan.Research on ship deformation monitoring based on SVD matrix algorithm[J].Ship Science And Technology,2018,40(7A):19-21.DOI:10.3404/j.issn.1672-7649.2018.7A.007.(in Chinese)

[5] 王宇,刘旭东.基于光学图像识别的船体变形量检测技术研究[J].舰船科学技术,2018,40(8A):7-9.

WANG Yu, LIU Xudong.Research on detection technology of hull deformation based on optical image recognition[J]. Ship Science and Technology, 2018,40(8A):7-9.DOI:10.3404/j.issn.1672 - 7649.2018.8A.003. (in Chinese)

[6] 陈典,程良伦.支柱式数字胎架控制系统的设计与应用[J].组合机床与自动化加工技术,2013(11):80-84.

CHEN Dian, CHENG Lianglun.Design and application of strutted NC mould bed control system[J].Modular Machine Tool & Automatic Manufacturing Technique, 2013(11):80-84.

[7] 袁萍,徐红昌,李威昂，等.新型造船活络头通用胎架的研究[J].船舶工程,2014,36(3):95-98.DOI:10.13788/j.cnki.cbgc.2014.0086.

YUAN Ping, XU Hongchang, LI Weiang, et al.Development of a new adjustable mould bed for shipbuilding[J]. Ship Engineering,2014,36(3):95-98.DOI:10.13788/j.cnki.cbgc.2014.0086.

[8] CHEON S U, KIM B C, MUN D. Counter-deformed design of ship structural parts using geometric shape deformation based on welding distortion estimation[J]. Journal of Marine Science and Technology,2015,20(3)：395-396. DOI:10.1007/s00773-014-0296-8.

[9] 顾永凤,谢荣.船舶工业4.0模式下智能化柔性胎架系统的开发[J].江苏船舶,2016,33(3):29-31.DOI:10.19646/j.cnki.32-1230.2016.03.009.

[10] 宋俊杰,于洋,王健,等.基于船舶曲面分段数控胎架的柔性化制造技术研究[J].船舶与海洋工程,2016,32(2):63-68. DOI：10.14056/j.cnki.naoe.2016.02.012.

SONG Junjie, YU Yang, WANG Jian, et al.Research on flexible manufacturing technology based on jigs for curved hull block[J]. Naval Architecture and Ocean Engineering, 2016,32(2):63-68.DOI：10.14056/j.cnki.naoe.2016.02.012.(in Chinese)

[11] 苏一丹,陈爱国,徐曼平,等.数控胎架系统的设计及研究[J].广东造船,2016,35(6):49-52.

SU Yidan, CHEN Aiguo, XU Manping, et al. Design and research on NC mo-uld bed system[J].Guangdong Shipbuilding,2016,35(6):49-52. (in Chinese)

[12] 徐江敏,刘李明,林青,等.基于模糊神经网络滑模控制的船用螺旋桨磨抛并联机器人抗抖振研究[J].江苏科技大学学报(自然科学版),2017,31(6):751-756.DOI:10.3969/j.issn.1673-4807.2017.06.011.

XU Jiangmin, LIU Liming, LIN Qin,et al. Study on parallel robot of fuzzy neural network sliding controller[J].Journal of Jiangsu University of Science and Technology (Natural Science Edition),2017,31(6):751-756.DOI:10.3969/j.issn.1673-4807.2017.06.011.(in Chinese)

[13] KUMAR V, RANA K P S, KLER D. Efficient control of a 3-link p-lanar rigid manipulator using self-regulated fractional-order fuzzy PID con-troller[J]. Applied Soft Computing Journal,2019(82)：105531.DOI:10.1016/j.asoc.2019.105531.

[14] ZHOU Haibo,CHEN Rui, ZHOU Shun,et al.Design and analysis of a drive system for a series manipulat-or based on orthogonal-fuzzy PID control [J].Electronics,2019,8(9)：1051.DOI:10.3390/electronics8091051.

[15] NITHILASARAVANAN K, THAKWANI N, MISHRA P, et al. Efficient control of integrated power system using self-tuned fractional-order fuzzy PID controller[J].Neural Computing and Applications,2019,31(8)：4137-4155.DOI:10.1007/s00521-017-3309-9.

[16] 王爱增,何川,赵罡.基于曲率单调变化的空间非均匀三次B样条曲线的构造方法[J].计算机辅助设计与图形学学报,2020,32(1):140-146. DOI: 10.3724/SP.J.1089.2020.17913.

WANG Aizeng, HE Chuan, ZHAO Gang.A method of designing non-uniform cubic B-spline curve basedon monotone curvature[J].Journal of Computer-Aided Design & Computer Graphics,2020,32(1)140-146. DOI: 10.3724/SP.J.1089.2020.17913.(in Chinese)